课程思政理念下概率论与数理统计教学改革的探索与实践*

张艳 陈美蓉 王亚军 姚香娟 （中国矿业大学数学学院）

中共教育部党组于2017年12月发布了《高校思想政治工作质量提升工程实施纲要》，详细规划了“十大育人”体系。其中在课程育人质量提升体系中，提出要大力推动以“课程思政”为目标的课堂教学改革，实现思想政治教育与知识体系教育的有机统一。如何在概率论与数理统计课程的教学过程中进行课程思政，笔者从教育理念、教学原则和实践路径等方面进行了探析。

一 要更新理念，在教学过程中落实立德树人的根本任务

立德树人是高校立身之本。课堂教学是育人主渠道。如何在课堂教学过程中实现立德树人这一根本目标，习近平总书记在全国高校思想政治工作会议的讲话中指出，要坚持把立德树人作为中心环节，要用好课堂教学这个主渠道，思想政治理论课要坚持在改进中加强，提升思想政治教育亲和力和针对性，满足学生成长发展需求和期待，其他各门课都要守好一段渠、种好责任田，使各类课程与思想政治理论课同向同行，形成协同效应。课程思政就是对习近平总书记所要求的“同向同行”和“协同效应”的一种积极回应，其要义在于强调高校各类课程都要发挥思想政治教育作用。

在课程思政理念下，进行概率论与数理统计课程的教学改革，任课教师应从育人的本质要求出发，提高自身的育德意识和育德能力，围绕立德树人这一根本任务，充分发掘和运用概率论与数理统计学科中蕴含的思想政治教育资源，凸现其在知识传授、能力培养和品质塑造等方面的教育价值。在实践中要以强化教学过程中的思想政治教育功能为核心目标，创新教学方法、丰富课程内涵、优化教学设计、改进课堂管理，通过课前、课中、课后、线上和线下等多个环节多种方式融入社会主义核心价值观的精髓要义，引导学生树立正确的人生观、价值观、世界观，传播弘扬马克思主义科学理论，发挥概率论与数理统计课程的思想政治教育作用。

二 概率论与数理统计课程思政的基本原则

（一）融合性原则

所谓融合，就是在教学过程中将思想政治教育元素融入学科知识载体，将知识传授和价值引领有机地结合起来，采取潜移默化、循循善诱的方式实现立德树人润物无声。概率论与数理统计的数学课程属性决定了其思想政治教育功能的潜隐性，这就要求任课教师深入挖掘概率知识的德育内涵，找准时机，合理融入，契合学生成长发展的需求和期待，实现“课程承载思政，思政寓于课程”的相融相合。

（二）明确性原则

在课程思政理念下，概率论与数理统计属于“隐性思政”课程，这就决定了在教学改革过程中实现思想政治教育功能应遵循明确性原则。无论是教学目标的确立、教学方案的设计和实施还是教学反思和评价环节，都要彰显出思想政治教育的内涵。在确立教学目标时除了对学生在知识和技能方面的要求予以明确，还要针对价值观的培育和塑造给出合理清晰的描述。在教学方案的设计和实施过程中，要明确每个具体知识点可以进行哪方面的思政教育的融入，采取什么方式和载体途径融入，避免随意性和盲目性。教学反思环节要对课程思政教育的具体成效做出明确描述，以利于进一步的改革。在教学评价环节应对照“课程思政”的目标设置体现思政教育实施和成效的特色化多维度的评价指标。

（三）学生参与原则

苏联教育家苏霍姆林斯基说：“人的内心里有一种根深蒂固的需要——总想感到自己是发现者、研究者、探寻者。”因此在教学过程中，要充分尊重学生的主体地位，遵循学生参与原则，充分发挥学生的主体作用，有效激发学生思维参与、行为参与、情感参与和认知参与的积极性。脱离了学生的积极参与，课程思政将变成教学过程中附加的道德说教。因此在概率论与数理统计的教学过程中应结合大学生的实际生活，创设课程思政情境，让学生积极参与问题的发现和解决过程，还学生话语权，激发学生的思想碰撞和情感体验，以理论和实践相结合的方式，使学生在运用概率统计思想方法和思维策略解决实际问题的同时领会概率统计思想对理性认识和决策行为的指导作用，实现概率统计课程在知识传授、能力培养和品质塑造等方面的教育功能。

三 概率论与数理统计课程思政的实践路径

（一）加强知识发生过程教学，适时进行课程思政

知识发生过程教学是教师引导学生去揭示或感受知识发生的前提或原因, 知识概括或扩充的经过以及向前拓展的方向。加强知识发生过程教学不仅要把知识成果返璞归真地向学生揭示出来，还要让学生参与到知识的“再发现”和“再创造”过程，经历探索过程的磨砺，培养求真、求是、求善、求美的态度和精神。

在概率论与数理统计课程中，像概念的形成过程、问题的解决过程、结论的推导过程以及规律的被揭示过程等，都蕴含着“课程思政”的好时机。中国科学院院士、数学家林群先生曾指出微积分可以统一到一个哲学公式，带有比例数

概率论的两个基本定理：大数定律和中心极限定理，也可纳入前面的哲学框架。它揭示了追求真理的数字化过程：要经多道坎（即0.9，0.99，0.999，…）再将比例提到1，或者说，相对真理不可能100%正确，只能正确到90%，99%，99.9%，…在教学过程中可从对频率的稳定性如何进行严格地数学描述和理论证明的追问和解决过程中揭示出大数定律，概括得到大数定律以严格的数学形式表达了随机现象最根本的性质之一：大量的随机现象中平均结果的稳定性。这蕴含了确定性和随机性的辩证统一。中心极限定理则表明，在相当一般的条件下，当独立随机变量的个数不断增加时，不管它们原来服从什么分布，其和的分布都趋于正态分布。它揭示了产生正态分布变量的源泉，同时也是哲学中量变引起质变的典型例证之一。

（二）以问题为先导，通过“问题解决”进行课程思政

在教学过程中以问题为先导组织教学，通过提出问题—分析问题—解决问题来引导和推动学生采取自主、合作、探究等方式进行学习，促进学生实现知识的自主建构和能力的提升。在“课程思政”理念下，教师要精心创设生动的问题情境，利用概率知识揭示其深刻的内隐本质，帮助学生实现认知和技能的深化和固化，同时还要挖掘出其中的德育内涵，诠释知识背后的价值趋向和人文精神，实现知识传授和价值引领的有机结合。

举一个例子。《伊索寓言》中《孩子与狼》的故事大家耳熟能详。在教学中我们可以“故事中的村民对孩子的可信度是如何下降的”这个问题为先导，引导学生用概率语言来表示故事中的事件，并进一步推动学生利用概率知识解决上述问题。首先设事件A 为“小孩说谎”，事件B 为“小孩可信”，再假设“可信的孩子说谎的概率为0.1，不可信的孩子说谎的概率为0.5”，即

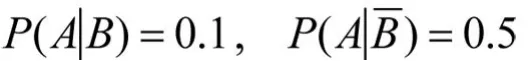
村民原来对这个孩子的印象是较为可信的，不妨设P(B)=0.8，在建立了概率模型并进行了合理假设之后，再引导学生把说谎的孩子的可信度用概率表达式表示出来，并利用概率方法计算出来。故事中的孩子第一次说谎之后，利用贝叶斯公式可以计算出村民对孩子的可信度改变为

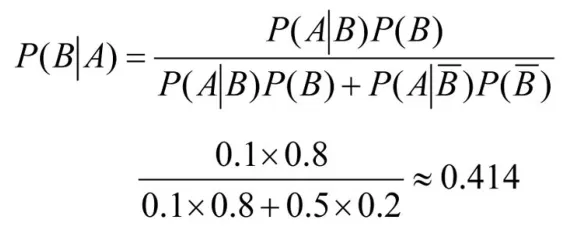
在此基础上，再一次利用贝叶斯公式可以计算出孩子第二次说谎之后，村民对孩子的可信度进一步下降，约为0.138.计算结果说明孩子说了两次谎之后，村民对他的可信度由原来的较高值下降为非常低的值。

故事中的孩子用生命为代价诠释了诚信的重要性。在用概率方法解决了这个问题之后，教师可以进一步挖掘其中的德育内涵，抓住时机进行课程思政。诚信是中华民族的传统美德，是一个人的立身之本。孔子曰：“人而无信，不知其可也。”我国古代历史典故中也有许多关于诚信的故事，比如商鞅徙木立信、曾子杀猪不欺子、黄金百斤不如季布一诺等等。在现代社会，诚信是公民必须恪守的基本道德准则之一，是社会主义核心价值观的基本内容之一。

（三）在案例和专题教学过程中进行课程思政

在教学过程中以课程思政为目标，选择典型案例并适时进行专题教学，不仅可以帮助学生实现知识学习的融会贯通和新旧迁移，提高分析问题、解决问题的能力，而且可以为学生提供浓浓的思政元素丰富的“营养汤”，这是彰显德育功能的有效途径。

比如在小概率事件原理的专题教学中，可以从大家熟知且贴近生活的一些俗语入手。“常在河边走，哪有不湿鞋的”是人们总结出的经验教训，可以从概率角度解释为“在河边走一次，湿鞋的概率很小”，但走的次数多了，“湿鞋”就几乎必然发生了，这也警示我们不可忽视小概率事件的影响。习近平总书记在2013年6月召开的党的群众路线教育实践活动工作会议上指出：“‘祸患常积于忽微，而智勇多困于所溺．’养成勤正衣冠的习惯，能收到防微杜渐之效，能有效避免‘积羽沉舟，群轻折轴’。”这段话也闪烁着“小概率事件原理”的理性光芒。教师可以借此告诫同学们，学习的小错误、行为习惯上的小毛病、为人处事上的不当之处，如果不及时纠正，日积月累，就会酿成大错大祸。