时频信号的非参数加窗稀疏协方差迭代分析法*

王悦斌，张建秋

(复旦大学智慧网络系统研究中心和电子工程系·上海·200433)

0 引 言

多分量非平稳信号的瞬时幅度和频率估计在诸多领域(例如导航、制导、振动、语音分析、雷达系统和生物医学等[1-4])扮演着重要的角色。然而，传统的谱估计方法只能揭示全局的频谱分布，无法分析出瞬时幅度和频率随时间变化的信号。鉴于此，时频分析(Time-Frequency Analysis, TFA)方法可用来估计信号时频两域的联合分布。其中最为人所熟知的是短时傅里叶变换(Short-Time Fourier Transform, STFT)[5]，该方法假设非平稳信号在较短的时间窗内是近似平稳的，这样就可对短时窗内的信号做傅里叶变换，来获得该时间窗内信号的局部频率特性。

然而，在对非平稳信号进行STFT分析时，一般要求时间窗内的信号是平稳的。但是当信号具有非常强的非平稳性时，就要求时间窗必须很短，这样其能量集中度必将下降。为了提高随时间变化的频谱的能量集中度，提出了Wigner分布(Wigner Distribution , WD)[6]分析法。WD分析法不需要任何窗函数，因此具有较好的时频能量集中度，但该方法具有非常强的交叉项效应。此外，在基本S变换的基础上，也发展出了广义S变换[7]，它试图采用多参数的窗函数，来灵活调节窗函数的形状，进而为克服时频分辨率单一的缺点提供了一条新途径。

近几年，研究者一直致力于改善时频分析的性能。例如，针对STFT中时间分辨率和频率分辨率必须进行折衷选择的缺点，文献[8]提出了自适应的STFT(Adaptive Short-Time Fourier Transform, ASTFT)算法。该算法能根据信号调频斜率的变化不断调节自身的STFT窗长度，从而使信号在调频斜率较小时具有较高的频率分辨率，在调频斜率较大时有较高的时间分辨率。然而，当存在多个复杂的信号分量时，该算法则无法给出不同信号分量要求的不同最优分析窗长度。文献[9]则提出了利用Capon方法对短时窗内的信号进行频谱估计，以获得窗内的局部频率特性，并随着窗的向前滑动，最终获得了信号时频两域的联合分布。

针对目前时频分析方法普遍存在的时频分辨率不足的缺点，本文基于传统的时频分析框架，给出了一种非参数加窗稀疏协方差迭代分析(Weighted Sparse Iterative Covariance-based Estimation，SPICE)[10]法。该方法首先给出了局部化窗内信号的非参数时频模型，进而利用加权最小二乘(Weighted Least Square，WLS)法求解优化。将WLS的加权矩阵构建问题转化为信号的广义协方差矩阵拟合问题，可利用加窗SPICE方法来获得短时窗内的局部频率特性。最后，采用滑动的时间窗函数获得时频分布图。结果表明：提出方法在噪声抑制和能量集中度等方面均优于文献报道的方法。

1 时频分析方法回顾

本文考虑的多分量时变非平稳信号的离散形式可描述为[9]

(1)

(2)

对于形如式(1)的非平稳信号，其统计特性(包括该信号的频谱特性)都会随着时间变化而变化，这意味着在对其进行分析和处理时不能将时域和频域截然分开。本文研究的时频分析方法就是为了将信号时域和频域特性结合起来以表征信号，并能对其进行分析和处理。

1.1 短时傅里叶变换STFT

在离散时间n和频率m上的离散STFT表达式为[5]

(3)

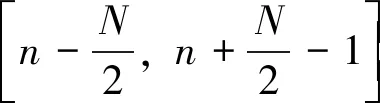
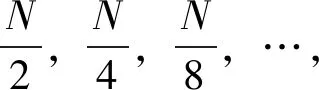
测不准原理表明，宽的时间窗可以获得高的频率分辨率，但是却可能无法检测到频率分量的快速变化；窄时间窗虽可以跟踪到频率分量的快速变化，却降低了频率的分辨率。两种极端的情况是：当N=1时，SSTFT(n,m)=y(n)；当N等于总的数据长度时，SSTFT(n,m)=DFT{y(n)}，即退化到离散傅里叶变换。因此，如何在保证时间分辨率要求的同时，获得最高的频率分辨率，是本文的主要研究内容。

1.2 Capon时频变换

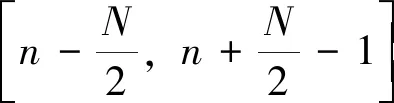
(4)

式中，gN=[gN(-N/2)，…，gN(N/2-1)]表示自适应数据的滤波器。该最优问题要求的是：尽可能保留频点m处的能量，而抑制其他频点的能量。上述约束优化问题借助于拉格朗日乘子法获得的解为

(5)

(6)

Capon法分辨率虽然较FFT有所提升，但其准确性和分辨率极易受到数据分段的影响[12]，这限制了其分析较短时间窗内信号的能力。

2 非参数化时频分析法

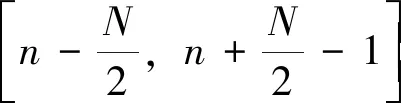
yn=Hx+ηn

(7)

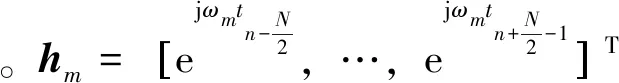
(8)

式中，W为加权矩阵。该问题的解为[12]

(9)

对于如何构造加权矩阵W，首先要考虑观测信号的广义协方差矩阵。假设信号和噪声相互独立，并且不同频率成分的信号不相关，则测量信号yn的协方差矩阵为

(10)

式中，IN×N表示N×N的单位阵。当W=R-1时，式(9)的均方误差最小[12]。这样，该问题即转换为如何估计协方差R。

2.1 加权SPICE 估计协方差

对于如何估计测量信号yn的协方差，SPICE考虑的问题模型如下[13]

(11)

式中，第1项为信号的协方差矩阵，第2项则为噪声的协方差矩阵。对比式(10)和式(11)，可以发现基于式的模型不仅可以用来实现稀疏谱估计，并且适应于非高斯噪声的情况。而对于{pm}的估计，SPICE则是通过如下最小化协方差拟合准则而实现[10]

(12)

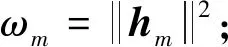
(13)

(14)

2.2 加窗非参数化时频分析

对于式(3)的STFT，常用的非矩形窗有高斯窗(Gauss)、汉宁窗(Hanning)和哈明窗(Hamming)等。这些窗函数对于信号频谱泄漏的大小及频谱分辨率等方面的影响不同，因此可根据实际需求采用不同的窗函数。例如矩形窗主瓣窄，频率识别精度高；高斯窗则旁瓣小，幅度识别精度高。

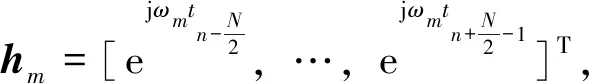
(a)矩形窗(a) Rectangle window

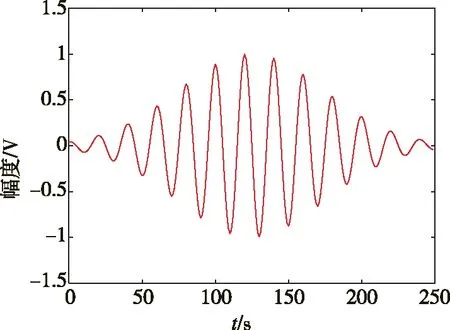
(b) 高斯窗(b) Gaussian window图1 不同窗内的信号时域图Fig.1 Signal of time domain in different window

(15)

(16)

由式(16)可以发现，测量信号的协方差矩阵依然具有式(11)的形式，这是因为噪声协方差依然可以表示为

(17)

此时，非矩形窗下的SPICE模型则变为

(18)

由式(12)～(14)可推导出，任意窗函数下在离散时间n和频率m上的非参数时频分析结果为

(19)

式(19)表明：加窗非参数化时频分析的结果包含了窗函数的信息，这也意味着其给出的时频分析法不再局限于矩形窗。与式(14)相比，式(19)中的频率导向矢量gm引入了窗内信号的非平稳性信息，因而在非矩形窗下的式(19)的分析结果更加精确。

3 仿真试验及结果分析

3.1 超分辨率谱估计

仿真实验中的采样点数设为N(N=120)，采样频率为1Hz。观测中待估计信号数目为K(K=4)，频率位置分别处于f1=0.05Hz、f2=0.06Hz、f3=0.20Hz、f4=0.32Hz，幅度大小依次为1、1、1、0.5。在观测中加入信噪比(Signal-to-Noise Ratio, SNR )为10dB的高斯白噪声，分别用FFT、Capon和SPICE进行谱估计。离散化频率间隔为0.002Hz，其中Capon数据的分段长度L(L=15)，加窗SPICE迭代次数为J(J=6)。

图2为100次蒙特卡洛仿真下的平均谱估计结果曲线，可以看到，FFT谱估计结果(图2(a))的主瓣宽度较宽，且对旁瓣的抑制效果较差，无法完全分离2个频率差异较小的信号分量；Capon(图2(b))对旁瓣的抑制效果有提升，但是依然无法完全分离出2个频率差异较小的信号分量；由图2(c)可以看出，SPICE算法不仅对旁瓣的抑制效果较好，且能够基本分离出2个频率差异较小的信号分量。

减小信号观测数量至N(N=60)，保持其他实验条件不变，分别采用这3种算法进行谱估计。

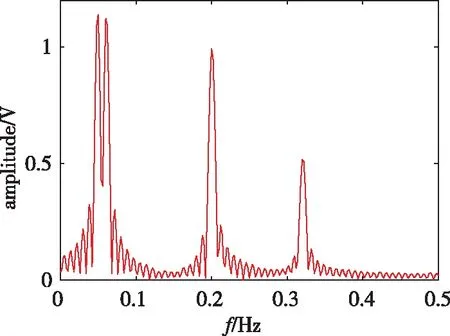
(a)傅里叶变换(a) FFT

(b)卡彭(b) Capon

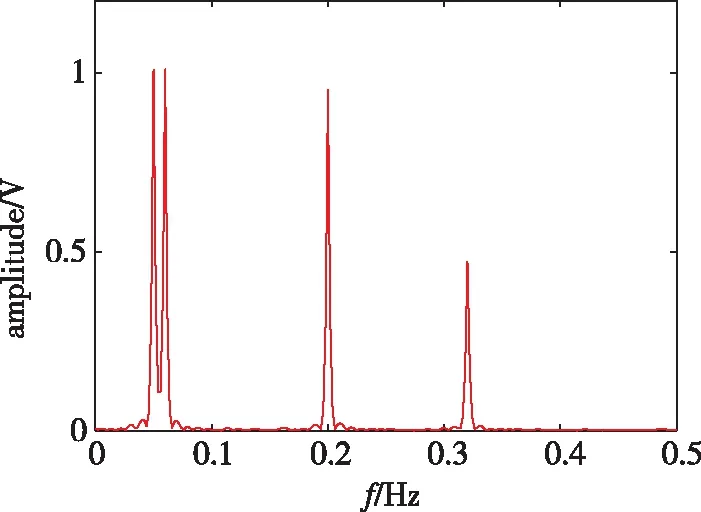
(c) 加窗SPICE(c) Windowed SPICE图2 多分量信号谱估计结果Fig.2 Spectrum estimations of multi-components signal

由仿真条件可知，理论上最小频率分辨为1/N(约为0.167)，大于信号分量的最小频率间隔0.01。图3为100次蒙特卡洛仿真下的平均谱估计结果曲线，可以看到，FFT和Capon均无法区分出2个频率差异很小的信号分量；SPICE算法依然可以检测出4个信号分量，分离效果和抑制旁瓣的能力更好，谱估计结果达到最佳。

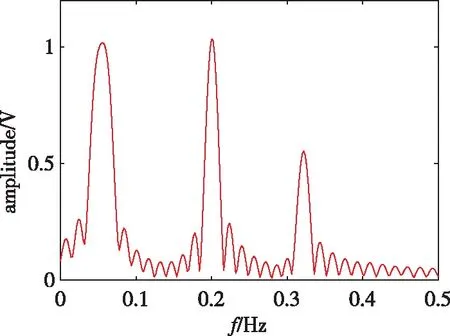
(a)傅里叶变换(a) FFT

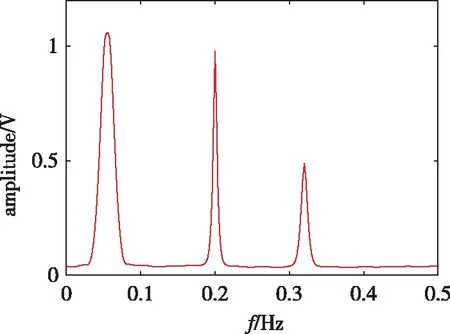
(b)卡彭(b) Capon

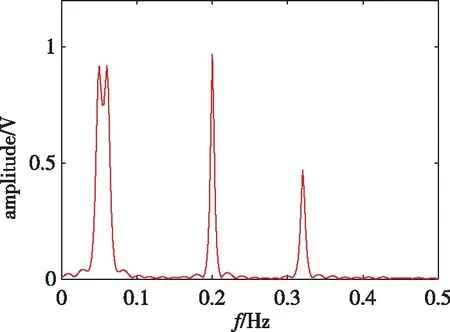
(c) 加窗SPICE(c) Windowed SPICE图3 超分辨率谱估计结果Fig.3 Super-resolution spectrum estimations

3.2 多分量信号的时频分析

考虑到多分量时变非平稳信号的一般形式，本文将信号的线性和非线性调频、信号分量的动态出现和消失等情况联合起来进行分析，仿真信号的具体形式如下

(20)

仿真信号的采样频率为512Hz，信号长度为10s，信噪比为0dB。该测量信号真实的时频分布如图4所示，信号分量间出现了一段最小载频差异为10Hz的区域。分别采用STFT、基于Capon的时频分析法和本文方法对仿真信号进行分析，如图3所示。所有算法均采用矩形窗，窗的长度为N(N=64)，窗的移动步长为N/4。离散化频率间隔为1Hz，其中Capon数据分段长度为L(L=15)，加窗SPICE的迭代次数为J(J=6)。

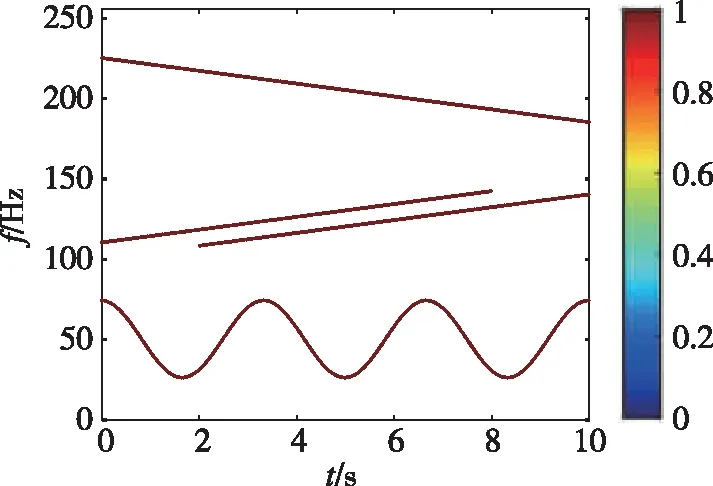
图4 观测信号的真实时频分布图Fig.4 Ground-truth time-frequency distribution of measured signal

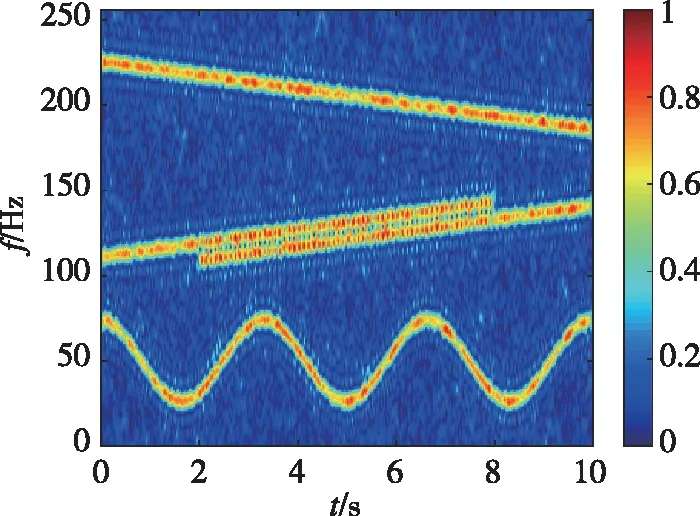
(a) 短时傅里叶变换(a) STFT

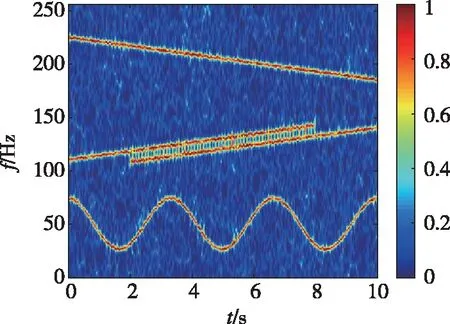
(c)加窗SPICE估计法(c) Windowed SPICE method图5 矩形窗的时频估计结果Fig.5 Time-frequency distribution estimations with rectangle window

可以看出，STFT算法(图5(a))的时频脊线较粗，频率分辨率较差，且旁瓣抑制能力较差；基于Capon的时频谱(图5(b))的能量集中度较STFT有所提高，但其噪声抑制能力较差。本文方法的时频谱如图5(c)所示，其噪声抑制能力较好，时频脊线更细，能量集中度最佳。

保持其他实验条件不变，将上述试验中的矩形窗改为高斯窗，得到如图6的实验结果。可以看出，STFT算法(图6(a))的时频脊线变粗，频率分辨率较差，且旁瓣抑制能力得到增强；基于Capon的时频谱(图6(b))噪声抑制的能力提高，但能量集中度下降，基本与STFT相当。本文方法的时频谱如图6(c)所示，其噪声抑制能力较好，时频脊线更细，能量集中度依旧最高。

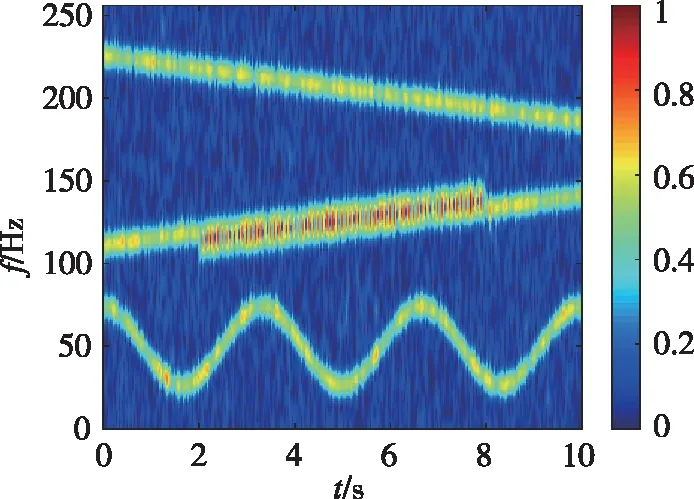
(a)短时傅里叶变换(a) STFT

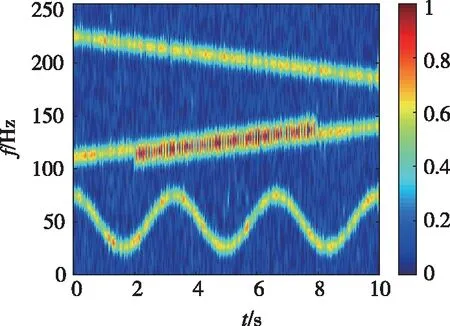
(b)卡彭估计法(b) Capon method

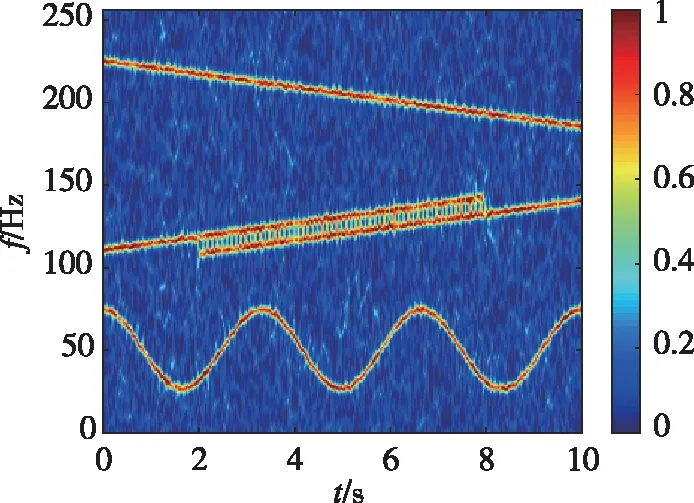
(c)加窗SPICE估计法(c) Windowed SPICE method图6 高斯窗的时频估计结果Fig.6 Time-frequency distribution estimations with Gaussian window

4 结 论

针对多分量非平稳时变信号，本文提出了一种非参数化稀疏协方差迭代的时频分析法。提出方法同样基于传统时频分析的框架，即利用局部化矩形窗函数来分析信号的局部频率特性。对于窗内信号，本文采用非参数化时频模型，并借助WLS算法，获得了时频谱估计结果。其中，针对WLS加权矩阵的构建，本文利用加权SPICE对广义噪声协方差矩阵进行了迭代估计。此外，本文考虑了非矩形窗时的非参数化时频模型的修正问题，适用于各种类型的窗信号。提出方法对于噪声谱有很好的抑制效果，同时兼具更高的频率分辨率，这一优越性在仿真对比试验中得到了充分体现。