反向曲线客货共线铁路桥梁车桥耦合分析
2019-04-19杨静静孙加林柯在田
杨静静,孙加林,柯在田
(1.中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081; 2.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心,北京 100081)
随着列车运营速度的提高及重载铁路的发展,列车与桥梁的动力耦合作用越来越引起重视[1-4]。目前车桥耦合研究主要针对直线桥梁,曲线桥梁尤其是反向曲线桥梁的车桥耦合研究很少。我国的《铁路桥涵设计基本规范》规定“桥上应避免采用反向曲线,大中桥宜设置在直线上。困难条件必须设置在曲线上时,慎用最小曲线半径。跨度大于40 m或桥长大于100 m的明桥面桥,宜设在半径大于1 000 m的曲线上”。而本文的某改线工程新建客货共线线路由于受到地形条件的限制,有一段反向曲线在正线特大桥上,其中曲线1的半径为1 200 m,曲线2的半径为600 m,此线路设置突破了规范限值。《铁路桥涵设计基本规范》亦规定“特殊结构及代表性桥梁应进行车桥耦合动力响应分析”。当桥梁位于反向曲线时,桥上运营列车的安全和桥梁的受力更为不利。因此,本文针对该改线工程上的反向曲线客货共线铁路桥梁进行客车和货车的车桥耦合动力分析,对反向曲线桥梁上的车辆与桥梁动力响应进行评价。
1 车桥耦合系统动力分析理论
车桥耦合系统包含车辆子系统和桥梁子系统,两者通过一定的轮轨关系耦合。车桥系统的坐标系如下:将列车前进方向定义为x轴,将竖直向上方向定义为z轴,根据右手螺旋法则确定y轴方向,相应的3个转动自由度分别为θ,φ和Ψ。
1.1 车辆
单节车辆的动力方程为
(1)
式中:MV,CV和KV分别为单节车辆的质量矩阵、阻尼矩阵和刚度矩阵,基于Lagrange方程或达朗贝尔原理求得;FV为单节车辆所受的力向量,包括车辆重力、曲线引起的离心力及轮轨间作用力。
车辆通过曲线桥比直线桥多了离心力1项,情况更为复杂。当列车以速度v通过曲线半径为R的桥梁时,第i节车、第i节车第j个转向架、第i节车第j个转向架l位轮对产生的离心力FRci,FRtij和FRwijl分别为
(2)
(3)
(4)
式中:mci,mtij和mwijl分别为车体、转向架和轮对的质量。
这些离心力不仅直接作用于车体、转向架、轮对本身,对车辆的沉浮、横移、摇头运动产生影响,也会通过弹簧阻尼器及轮轨相互作用传递给桥梁。其中,车体沉浮、横移、摇头运动方程中对应的曲线离心力分量[5-7]分别为
(5)
(6)
(7)
式中:Fczi,Fcyi和FcΨi分别为车体沉浮、横移、摇头运动方程中对应的曲线离心力分量;JcΨi为车体绕z轴的转动惯量;g为重力加速度;α为车体中心处的超高角。
1.2 桥梁
采用有限元法建立桥梁子系统的动力方程为
(8)
式中:MB,CB和KB分别为桥梁子系统的总体质量矩阵、总体阻尼矩阵和总体刚度矩阵,MB和KB由有限元法求得,CB由比例阻尼法求得;FB为桥梁所受的力向量,即各节车辆对桥梁的作用力之和。
1.3 轮轨间相互作用关系
法向轮轨关系采用Hertz非线性接触理论;切向轮轨关系采用kalker线性理论确定蠕滑力。运用UM软件实时获取接触斑、蠕滑力[8]。
1.4 轨道不平顺
轨道不平顺指沿轨道方向的实际轨道接触面与理论平顺轨道面之间的偏差,包括高低不平顺、水平不平顺、轨向不平顺、轨距不平顺等。
本研究采用既有提速线轨道谱作为车桥系统的动力激励。在保证激扰频率一致的条件下,通过改变轨道不平顺的幅值模拟不同的线路几何状态。
根据《铁路线路修理规则》,线路各项偏差等级划分为4类,本文选用的不平顺对应舒适度管理标准,当车辆运行速度低于120 km·h-1时,高低不平顺容许限值为12 mm。
2 车桥耦合计算
某改线工程新建线路为单线无缝客货共线铁路,线路设计速度为120 km·h-1。由于受到地形条件的限制,有一段反向曲线在正线特大桥上。曲线1:半径1 200 m,由100 m缓和曲线+113.57 m圆曲线+100 m缓和曲线组成,实际设置超高为70 mm,根据曲线区段线路超高计算式(9)可得对应均衡速度为85 km·h-1;曲线2:半径600 m,由120 m缓和曲线+931.76 m圆曲线+120 m缓和曲线组成,实际设置超高为125 mm,根据曲线区段线路超高式(9)可得对应均衡速度为80 km·h-1;曲线1与曲线2之间有一段266.11 m的夹直线。在曲线2的小半径段列车限速100 km·h-1。
(9)
式中:h为曲线超高,mm。
桥梁计算区间位于圆曲线—缓和曲线—直线—缓和曲线—圆曲线范围内,该范围内桥梁梁部结构采用时速160 km客货共线铁路预制后张法简支T梁(钢横梁人行道方案),图号为通桥(2017)2101,该桥单线梁的横向布置如图1所示。
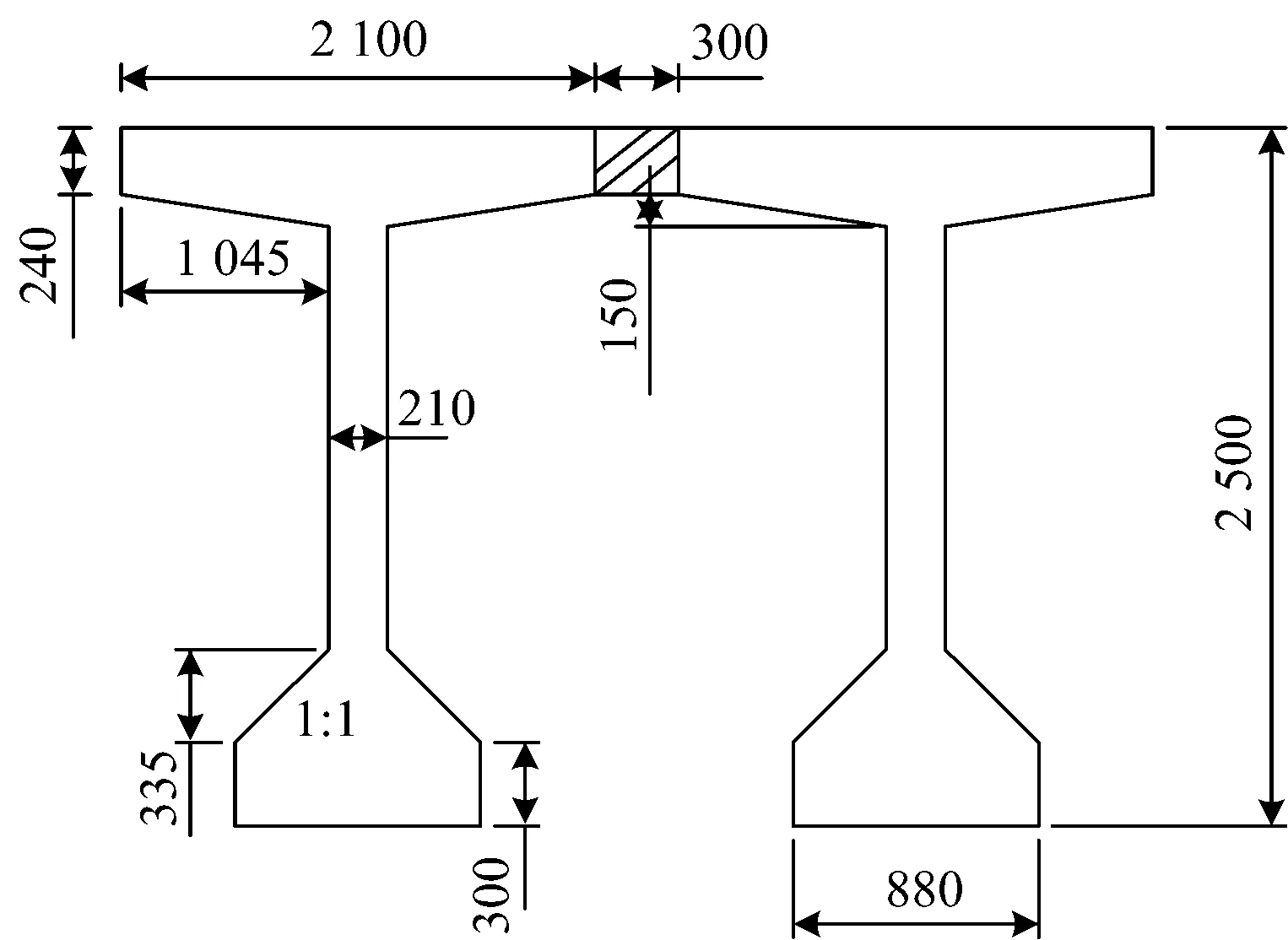
图1 单线梁的横向布置图(单位:mm)
利用UM软件建立车辆动力学模型,并生成曲线线路平面布置图,如图2—图4所示。
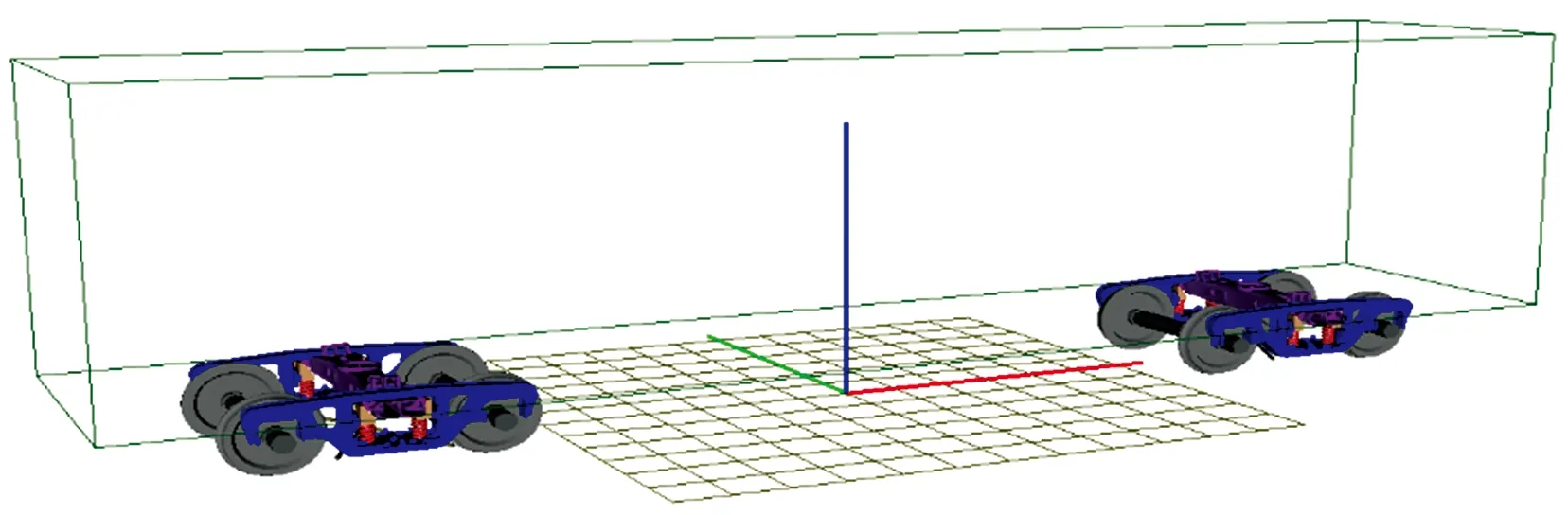
图2 单节重载货车

图3 单节普速客车
采用Midas有限元软件建立桥梁模型。主梁采用空间梁单元模拟,横隔板采用板壳元模拟;桥墩和承台采用空间梁单元模拟,墩底固结;桥梁支座采用主从节点模拟。结构阻尼采用瑞利阻尼,阻尼比取为0.02。单跨桥梁的动力分析模型如图5所示。
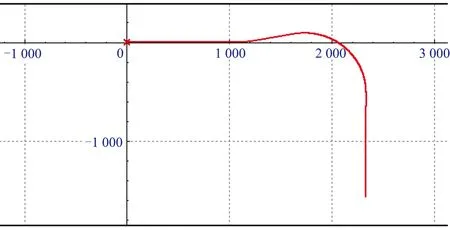
图4 曲线线路平面布置(单位:m)
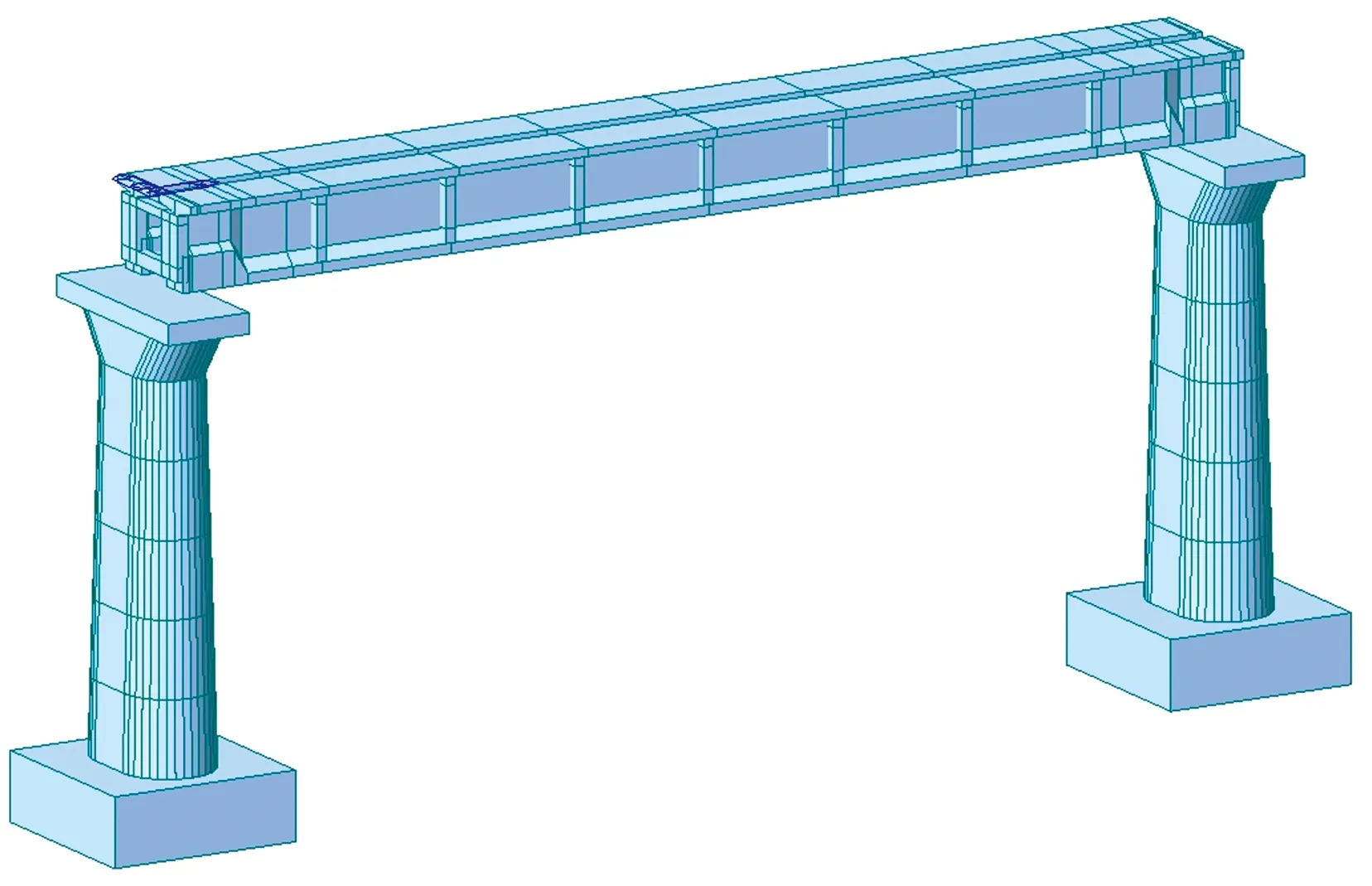
图5 32 m简支梁单跨有限元模型
在UM软件中输入轨道不平顺,进行车线系统动力分析,得到轮轨力时程输入桥梁的有限元模型,得到桥梁变形,将其与轨道不平顺叠加形成新的轨道不平顺,重新输入UM软件,重复上述步骤直至车辆和桥梁的动力响应满足精度要求。
下面分析20节普速客车、20节重载货车分别以60,80,100和120 km·h-1的速度通过该反向曲线时的动力性能。计算的车辆动力分析指标包括安全性指标(脱轨系数、轮重减载率和轮轴横向力)和平稳性指标(车体振动加速度);桥梁动力分析指标包括桥梁变形和桥梁振动加速度。
依据《铁道车辆动力学性能评定和试验鉴定规范》和《铁路线路修理规则》对车辆动力分析结果进行评价。车辆脱轨系数限值为1.0,轮重减载率限值为0.6,客车轮轴横向力限值为64 kN,货车轮轴横向力限值为106 kN,客车车体横向振动加速度限值为0.10g、垂向振动加速度限值为0.15g,货车车体横向振动加速度限值为0.50g、垂向振动加速度限值为0.70g。
依据《铁路桥梁检定规范》对桥梁动力分析结果进行评价。有砟轨道桥面垂向振动加速度限值为0.35g、横向振动加速度限值为0.14g;客车通行条件下,桥梁跨中横向振幅的通常限值为0.696 mm;货车通行条件下,桥梁跨中横向振幅的通常限值为2.08 mm。横向振幅的安全限值为3.56 mm。
3 计算结果及分析
3.1 客车
表1给出了客车车辆的动力计算结果。表中不满足规范要求的指标用加黑加粗显示。
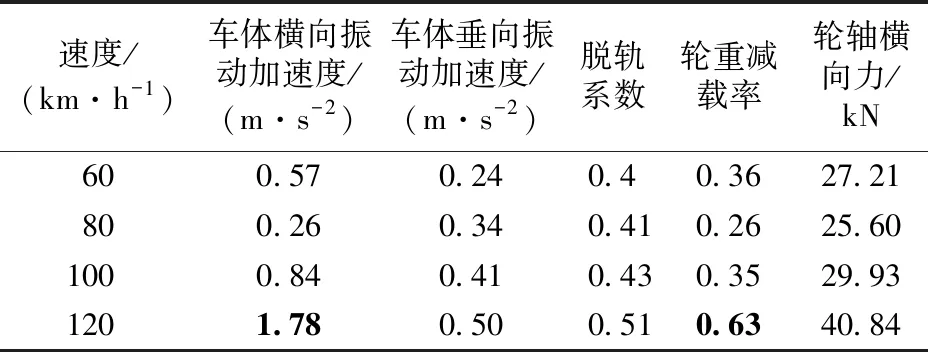
表1 客车动力计算结果
由表1可看出,当普速客车以60~120 km·h-1的速度通过该反向曲线时,除速度120 km·h-1下的车体横向振动加速度与轮重减载率外,其余各项动力响应满足规范要求。其中,车速120 km·h-1时在600 m小半径圆曲线段各动力指标出现最值,由于欠超高和运营速度的影响,车体横向振动加速度超过安全限值1 m·s-2、轮重减载率超过限值0.6。而实际上车辆在600 m小半径圆曲线段的限速为100 km·h-1,此时各项动力响应满足要求。图6和图7分别给出了车速100和120 km·h-1时的车体横向振动加速度和轮重减载率时程曲线。
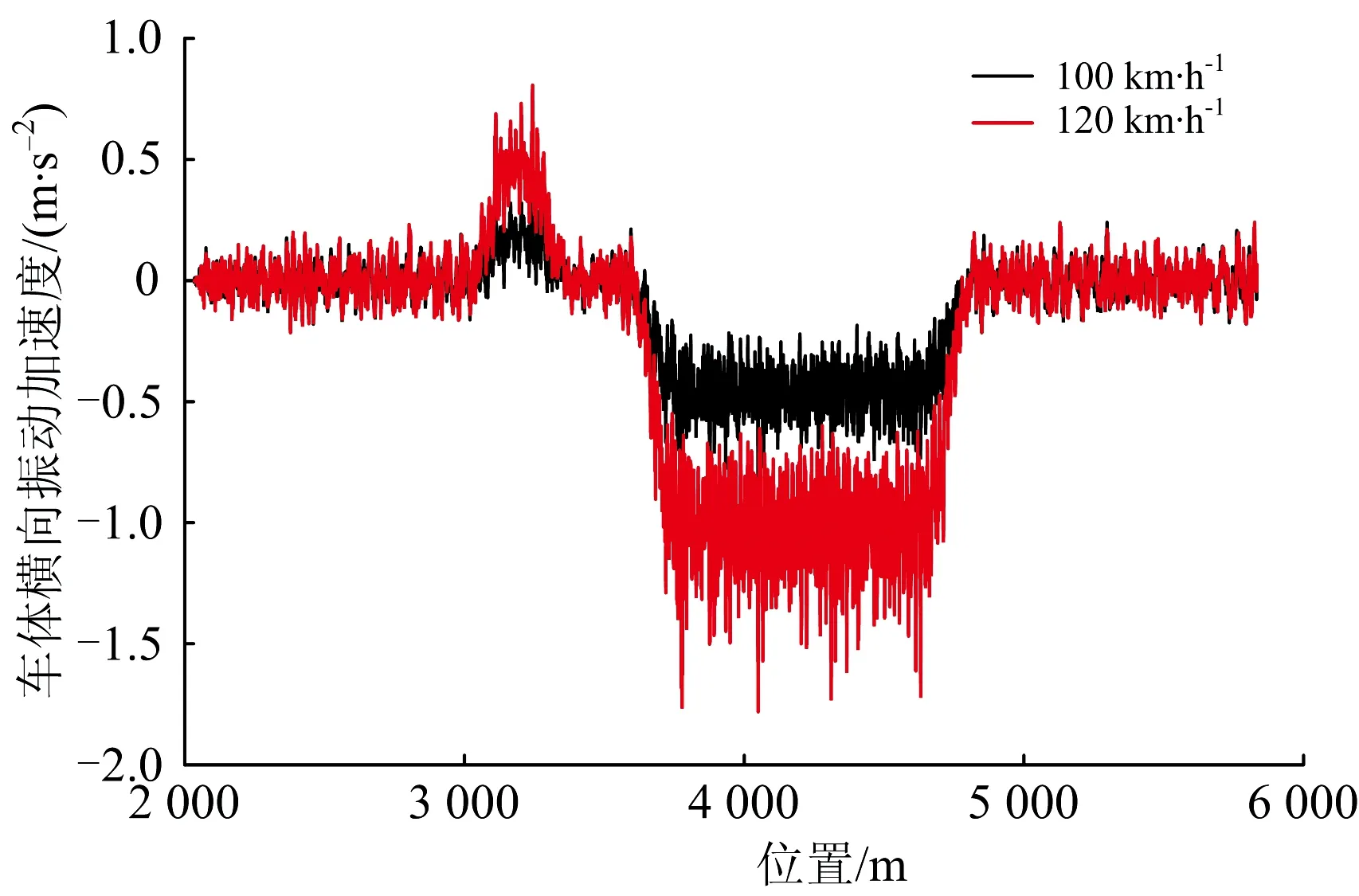
图6 客车车体横向振动加速度时程曲线
由于反向曲线的存在,列车运行过程中存在离心力和曲线超高的作用。随着车速的提高,车体垂向振动加速度逐渐增大;车体振动横向加速度在600 m小半径圆曲线段出现最大值,根据曲线超高设置,该曲线段对应的均衡速度为80 km·h-1,当车速为80 km·h-1(无欠超高或过超高)时车体横向振动加速度最小。因此反向曲线的存在对车体横向振动加速度的影响比垂向大。
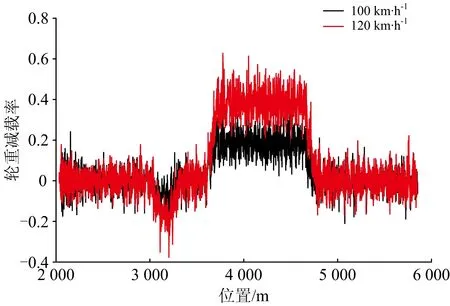
图7 客车轮重减载率时程曲线
桥梁在各工况下的动力响应见表2和表3。《铁路桥梁检定规范》中并未对垂向振幅做出规定,本研究列出桥梁跨中垂向动位移用于参考。其中,桥梁输出节点位置包括1 200 m半径圆曲线段、1 200 m半径缓和曲线段、600 m半径缓和曲线段和600 m半径圆曲线段的跨中节点。

表2 主梁跨中振动加速度计算结果
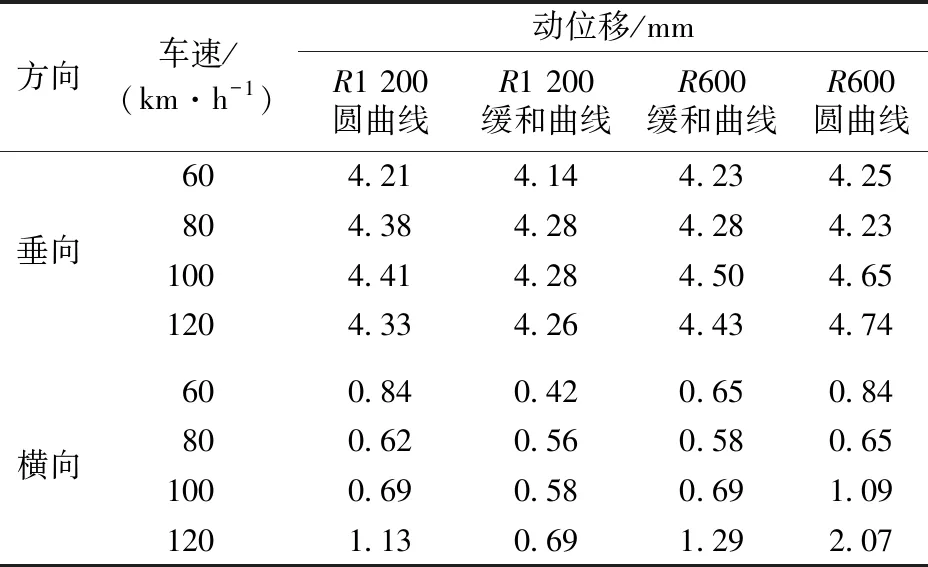
表3 主梁跨中动位移计算结果
由表2和表3可知,当普速客车以60~120 km·h-1的速度运行时,桥梁跨中动位移和桥梁振动加速度满足规范要求。
综合车辆与桥梁的动力响应,客车应在该反向曲线铁路桥梁的600 m小半径曲线段限速100 km·h-1。
图8给出了客车分别以100,120 km·h-1通过反向曲线桥梁时脱轨系数时程曲线,轮重减载率时程曲线见图7,桥梁在600 m小半径圆曲线段的跨中垂向、横向振动加速度时程曲线如图9和图10所示。
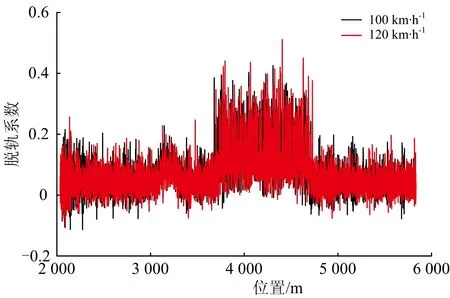
图8 客车脱轨系数时程曲线
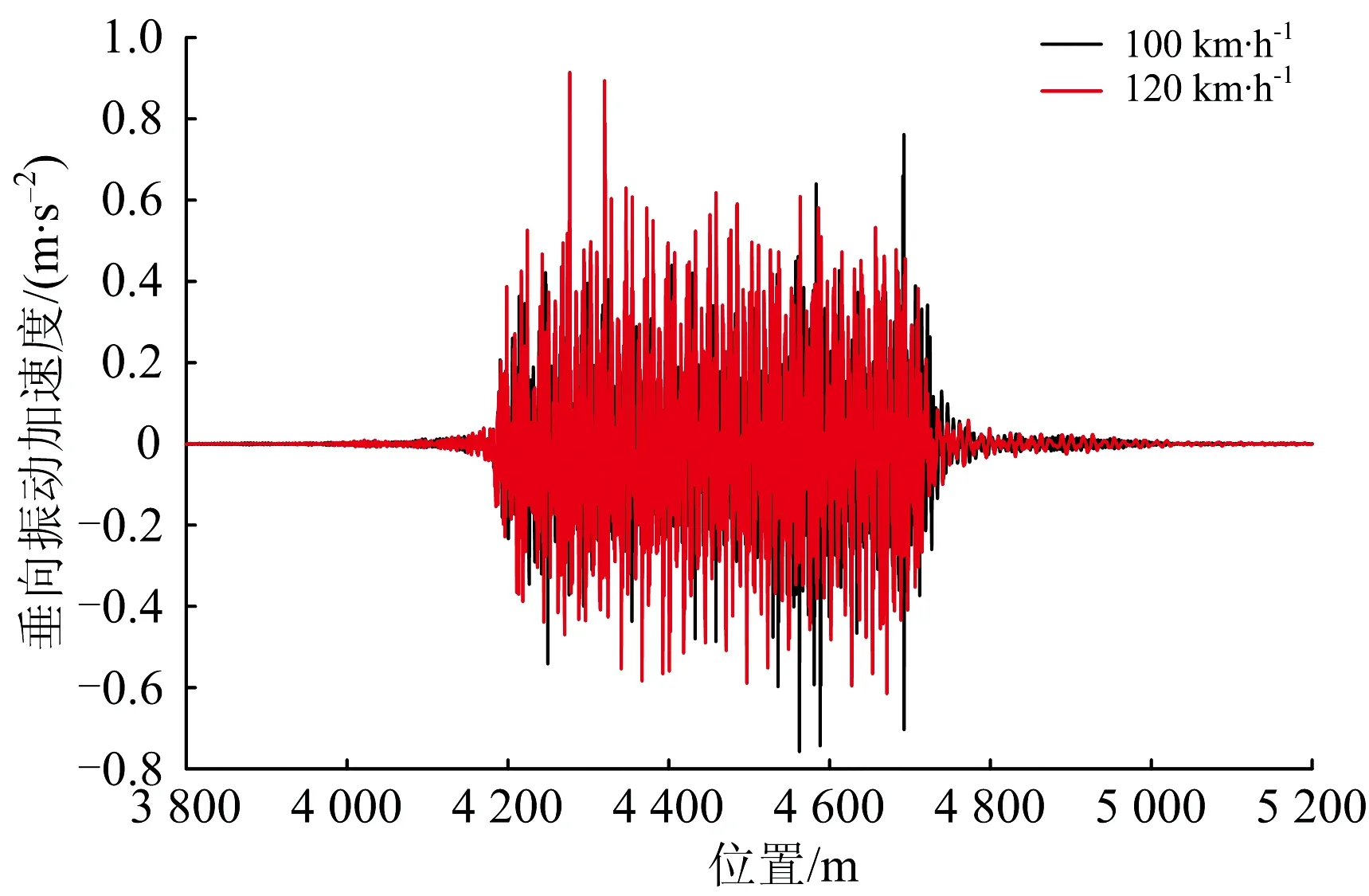
图9 客车通过桥梁时跨中垂向振动加速度时程曲线
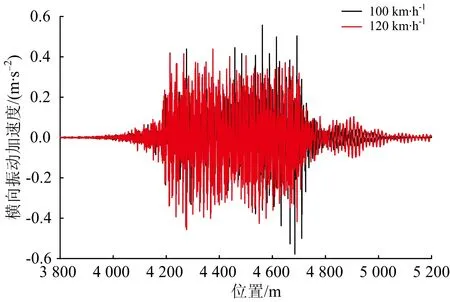
图10 客车通过桥梁时跨中横向振动加速度时程曲线
3.2 货车
表4给出了货车车辆的动力计算结果,表中不满足规范要求的指标用加黑加粗显示。
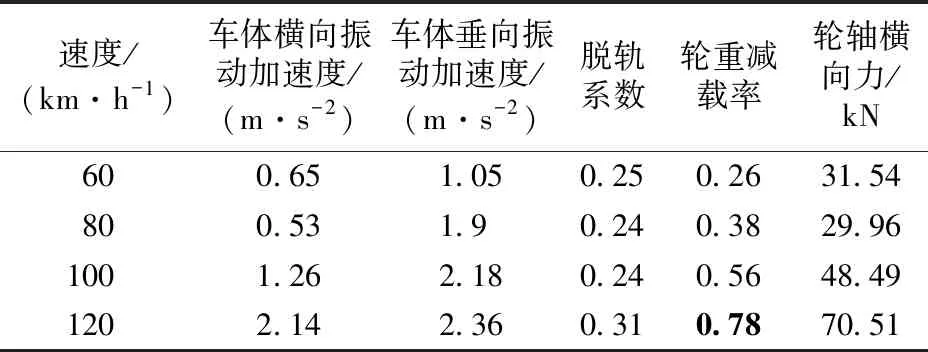
表4 货车动力计算结果
由表4可看出,当重载货车以60~120 km·h-1的速度通过该反向曲线时,除速度120 km·h-1下的轮重减载率外,其余各项动力响应满足规范要求。
桥梁在各工况下的动力响应见表5和表6,表中不满足规范要求的指标用加黑加粗显示。图11—图14给出了货车通过600 m小半径圆曲线段时桥梁跨中的振动加速度和动位移。
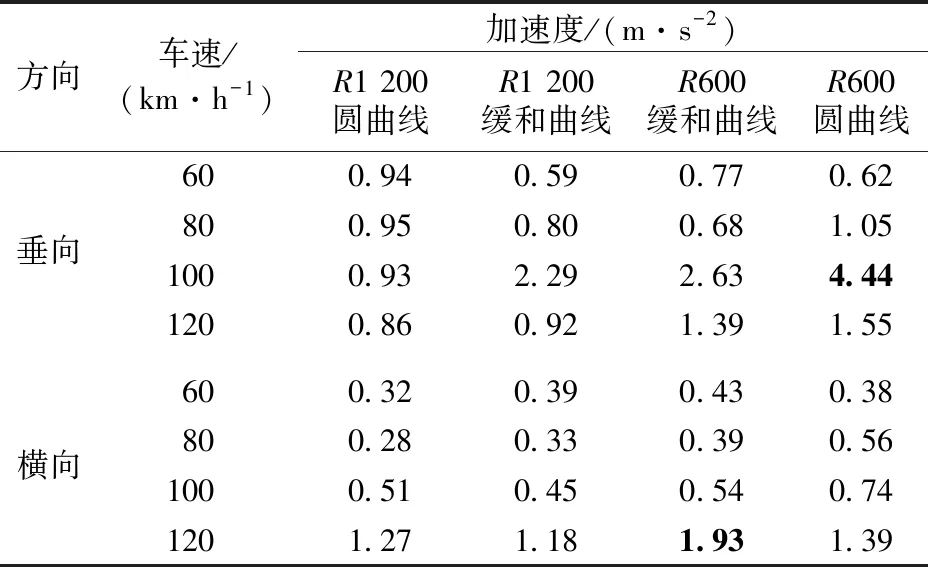
表5 主梁跨中振动加速度计算结果
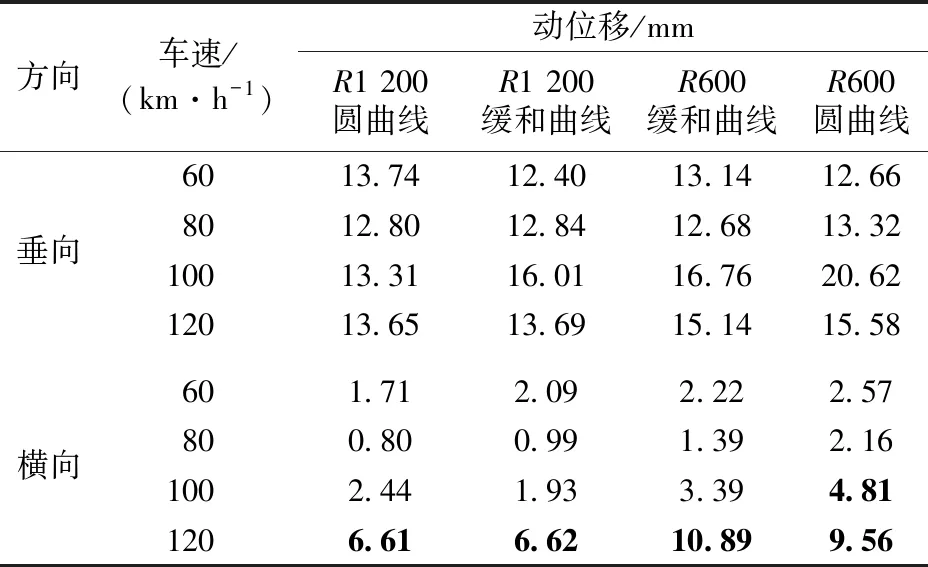
表6 主梁跨中动位移计算结果
可见:货车以100 km·h-1运行时桥梁垂向动位移和垂向振动加速度显著增大,这是由共振引起的。按照式(10)计算共振频率为3.39 Hz,与桥梁1阶竖向自振频率3.57 Hz接近,引起桥梁跨中垂向振动加速度达到4.44 m·s-2,高于限值3.5 m·s-2;货车以120 km·h-1运行时桥梁横向动位移和横向振动加速度显著增大,这也是由共振引起的。需要说明的是,尽管在通常情况下轨道不平顺的随机性特点不易导致横向共振,但在欠超高或过超高情况下,由于轮缘力的作用使得横向轮轨力方向不变,在车速一定的条件下方向不变的横向轮轨力对桥梁造成周期性作用,效果与垂向相近。按照式(10)计算共振频率为4.06 Hz,与桥梁2阶横向自振频率4.11 Hz接近,引起桥梁跨中横向动位移达到10.89 mm,高于安全限值3.56 mm,跨中横向振动加速度达到1.93 m·s-2,高于限值1.4 m·s-2。
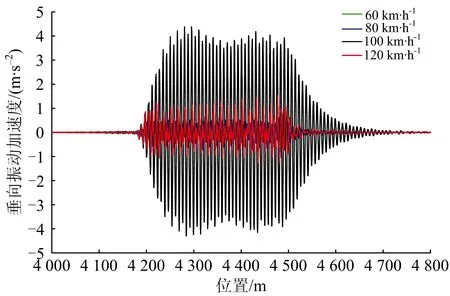
图11 货车通过600 m小半径圆曲线段时桥梁跨中垂向振动加速度
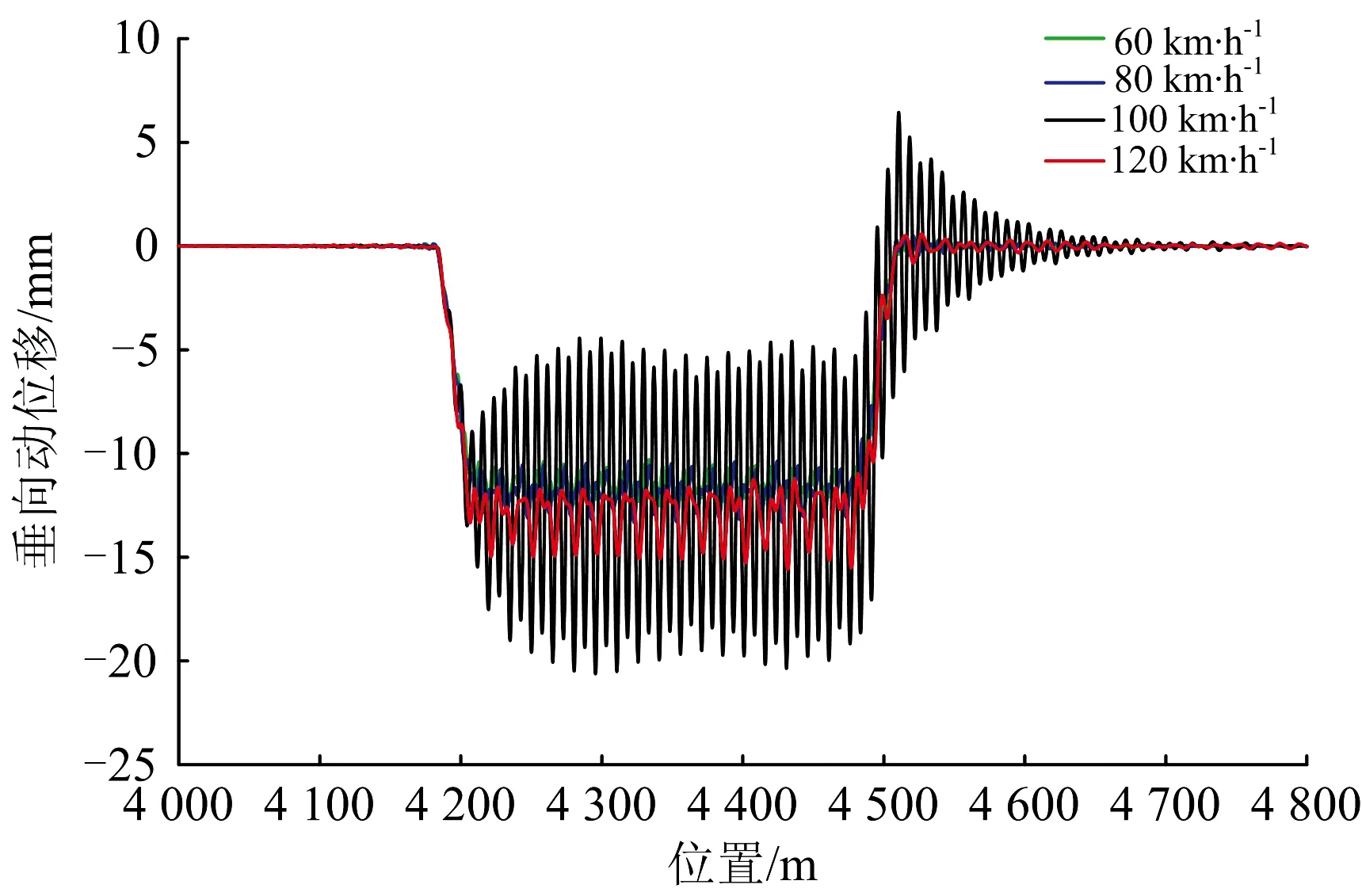
图12 货车通过600 m小半径圆曲线段时桥梁跨中垂向动位移
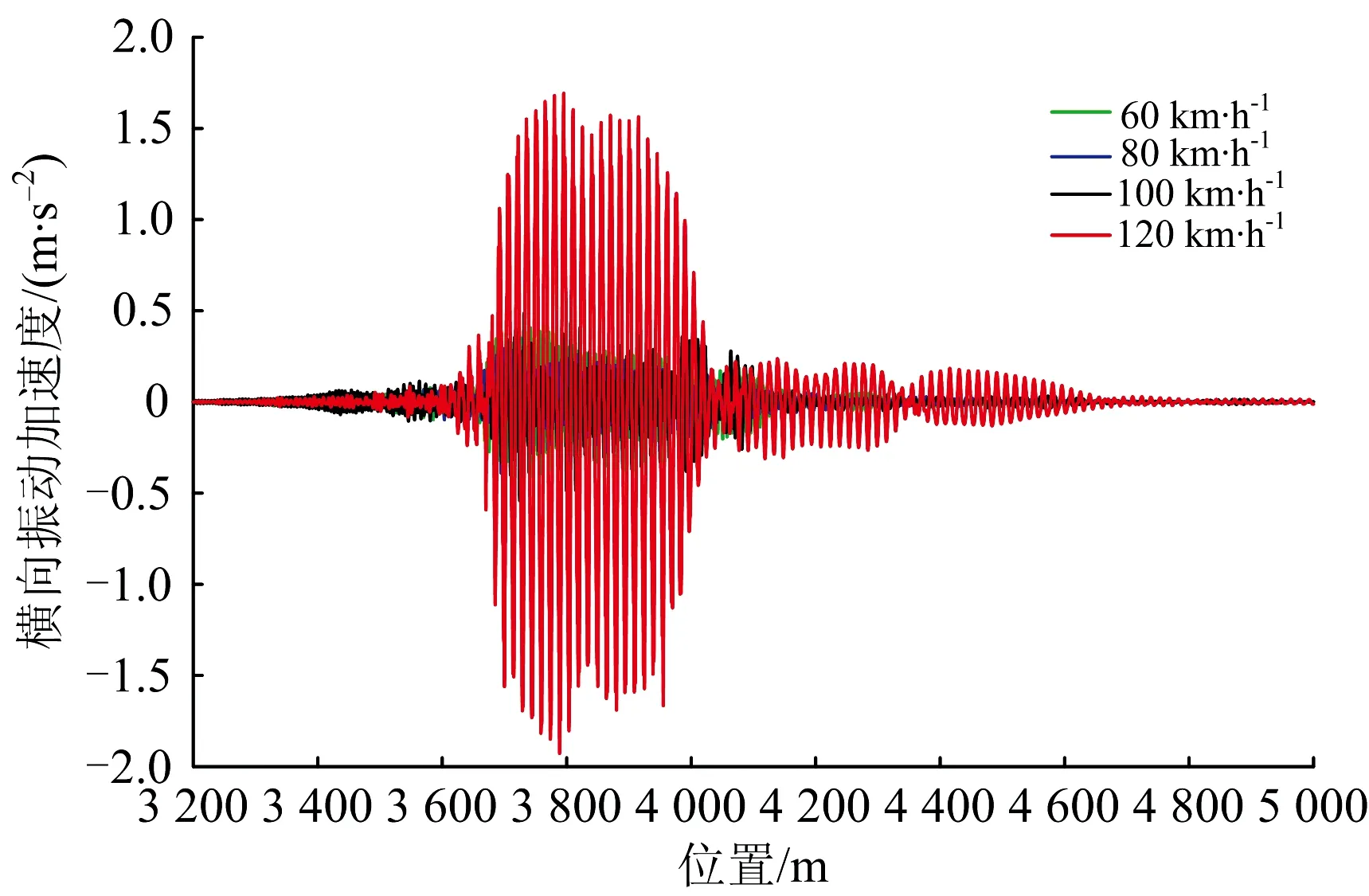
图13 货车通过600 m小半径缓和曲线段时桥梁跨中横向振动加速度
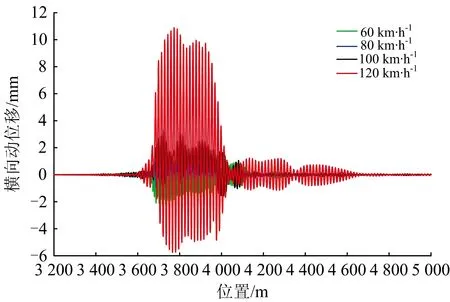
图14 货车通过600 m小半径缓和曲线段时桥梁跨中横向动位移
(10)
式中:L为车辆定距。
由表6可知:货车以100 km·h-1运行时桥梁跨中横向动位移达到4.81 mm,高于安全限值3.56 mm,这是由欠超高引起的。
综合车辆与桥梁的动力响应,该反向曲线铁路桥梁满足货车以80 km·h-1速度的安全运营要求。
图15和图16分别给出了货车以80 km·h-1速度通过反向曲线桥梁时脱轨系数、轮重减载率时程曲线。桥梁在600 m小半径圆曲线段的跨中垂向、横向振动加速度时程曲线分别如图17和图18所示。
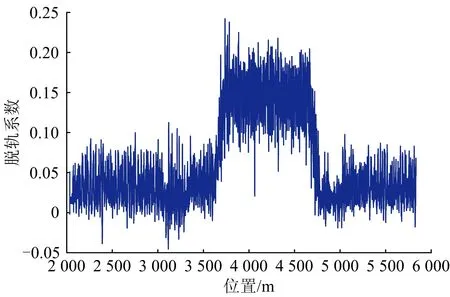
图15 货车以80 km·h-1速度通过反向曲线桥梁时车辆脱轨系数时程曲线
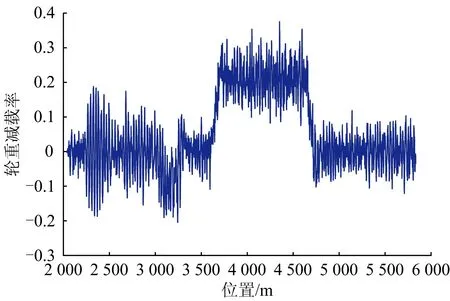
图16 货车以80 km·h-1速度通过反向曲线桥梁时车辆轮重减载率时程曲线
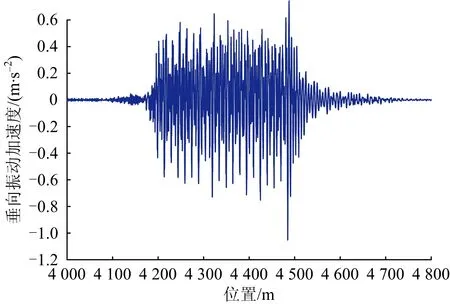
图17 货车以80 km·h-1速度通过反向曲线桥梁时桥梁跨中垂向振动加速度时程曲线
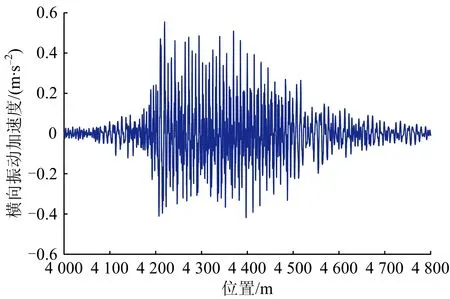
图18 货车以80 km·h-1速度通过反向曲线桥梁时桥梁跨中横向振动加速度时程曲线
《铁路桥梁检定规范》给出了桥梁跨中横向动位移的2个判别值:安全限值与通常值。桥梁横向振幅指标的意义在于避免过大的轨向不平顺影响车辆运行的安全性与平稳性[9],而本文车桥耦合分析表明脱轨系数、车体横向加速度等动力性能指标均基本满足要求。本次计算中,客车与货车的跨中横向振幅在4种速度下均高于通常值,而车辆在横向仍满足运行安全性、平稳性。因此,对于反向曲线铁路桥梁的横向动位移,应以安全限值作为评定标准。
4 结 论
(1)该反向曲线铁路桥梁满足货车80 km·h-1的安全运营要求,而客车应在该反向曲线铁路桥梁的600 m小半径曲线段限速100 km·h-1。
(2)由于反向曲线的存在,列车运行过程中存在离心力和曲线超高的作用。随着车速的提高,车体垂向振动加速度逐渐增大;车体横向振动加速度在600 m小半径圆曲线段出现最大值,根据曲线超高设置,该曲线段对应的均衡速度为80 km·h-1,当车速为80 km·h-1(无欠超高或过超高)时车体横向加振动速度最小。因此反向曲线的存在对车体横向振动加速度的影响比垂向大。
(3)反向曲线铁路桥梁动力响应,不仅需考虑曲线离心力与曲线超高,也受到不同车速、不同车辆定距对桥梁垂向或横向共振的影响。尽管在通常情况下轨道不平顺的随机性特点不易导致横向共振,但在欠超高或过超高情况下,由于轮缘力的作用使得横向轮轨力方向不变,在车速一定的条件下方向不变的横向轮轨力对桥梁造成周期性作用,效果与垂向相近。反向曲线铁路桥梁需警惕垂向及横向共振的影响,尤其在小半径曲线段桥梁的动力响应易超出安全限值。
(4)桥梁跨中横向动位移有2个判别值:安全限值与通常值。桥梁横向振幅指标的意义在于避免过大的轨向不平顺影响车辆运行的安全性与平稳性。对于反向曲线铁路桥梁,客车与货车的跨中横向振幅极易高于通常值而车辆在横向仍满足安全性、平稳性要求。因此,对于反向曲线铁路桥梁的横向动位移,应以安全限值作为评定标准。
