有缝线路上钢轨探伤车检测速度规划方法
2019-04-19孙次锁张玉华
孙次锁,秦 勇,刘 军,张玉华
(1.北京交通大学 交通运输学院,北京 100044; 2.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044; 3.中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081)
钢轨探伤车(简称探伤车)通过探轮在钢轨顶面滚动对钢轨内部伤损进行检测,探轮内部充满探轮液并安装有超声波换能器[1-2]。在探轮与钢轨之间需要喷洒耦合水,用以排出钢轨表面微观结构空间内的空气。超声波由超声波换能器发出,经过探轮内部介质与浸润在钢轨表面的水介质后进入钢轨,进入钢轨中的超声波能量越大,对钢轨伤损内部伤损检测能力越强。文献[3—4]分析了列车在铁路线路运行时的晃动现象,探伤车属于列车的一种,在运行过程中也会产生晃动,导致探轮沿钢轨顶面横向方向晃动,将影响进入钢轨的超声波能量大小;文献[5]认为探伤车伤损漏检的一个重要原因就是探轮对中不良;文献[6—7]通过研究自动对中系统解决了探轮对中严重不良的问题,但无法完全消除探轮对中偏差。钢轨表面微观结构中水越多、空气就越少,因此使用喷水密度表征钢轨表面微观结构中水的浸润程度。探轮对中偏差和喷水密度均会影响超声波的衰减,因此文献[8]中对探伤车检测过程中的灵敏度设置进行了探讨。在探伤车检测中发现:检测速度低,探轮对中偏差小,喷水密度大,超声波衰减小,有利于钢轨伤损检出,但检测效率低;检测速度高,探轮对中偏差变大,喷水密度变小,超声波衰减大,不利于钢轨伤损检出,但是检测效率高。因此,需要对检测速度进行控制和规划,以兼顾钢轨伤损检出效果和检测效率。
钢轨伤损是钢轨中超声波反射体的子类,超声波反射体包括已知的处于监控状态的伤损、螺孔裂纹、导线孔等,也包括钢轨中可以反射超声波的机械结构如轨底平面等。超声波反射体的检出效果可以用来评价伤损检出效果,若所有超声波反射体均被检出,有利于钢轨伤损的智能识别[9]和精准预警[10],则探伤车处于最佳检测性能状态,可以检出钢轨中的符合探伤车检测能力的伤损。
本文在建立超声波反射体动态检出效果模型的基础上,研究了检测速度、探轮对中偏差、喷水密度与反射体检出效果间的关系,在平直试验线上排除检测速度对探轮对中的影响后,建立喷水密度与超声波信号衰减间的关系模型。在某区间进行多次检测,过程中记录对中偏差与检测速度,通过分析钢轨中超声波反射体的检出情况,通过动态步长调节法对该区间下次检测时的检测速度进行规划。
1 超声波反射体动态检出效果模型
1.1 超声波反射体静态检出原理
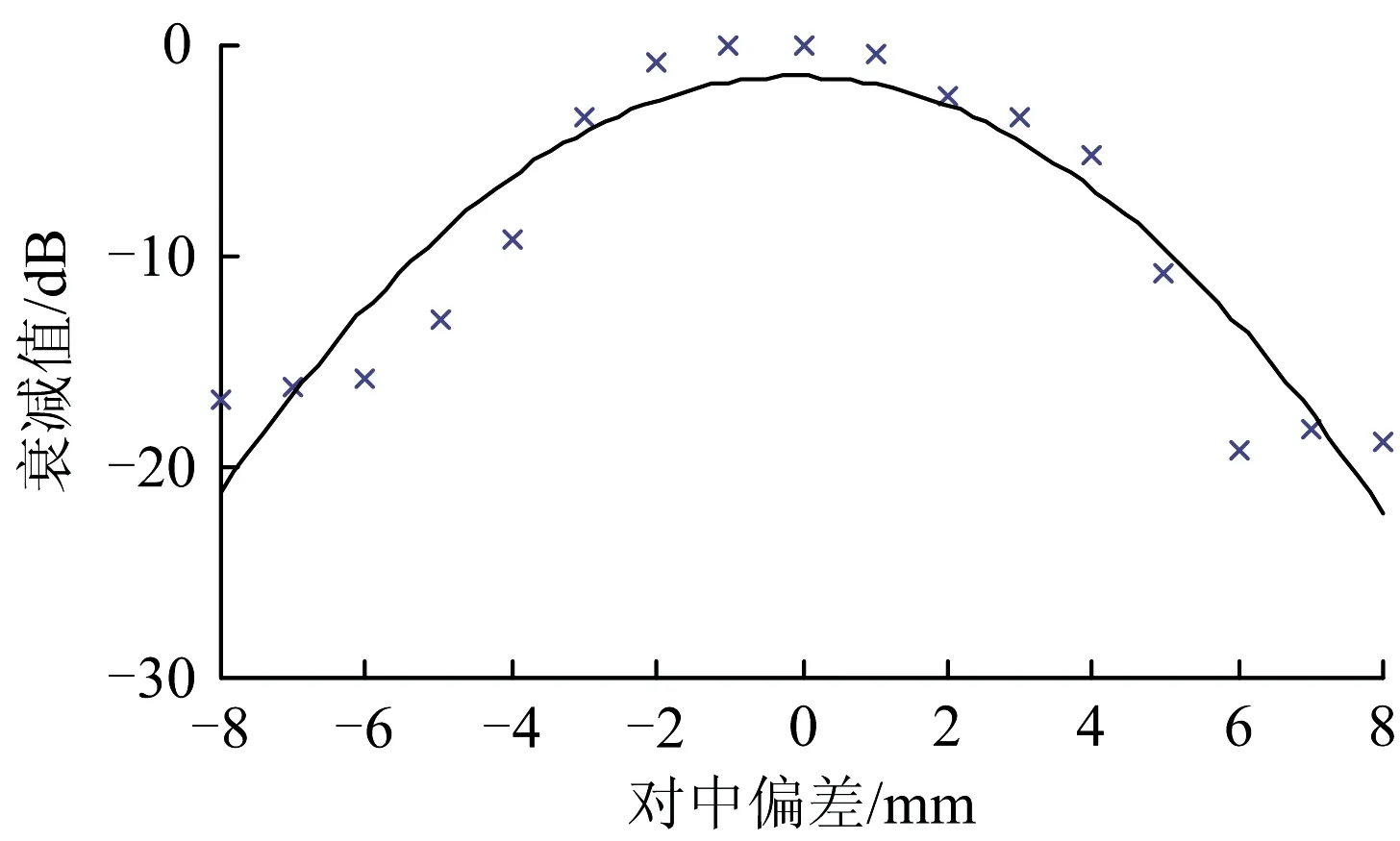
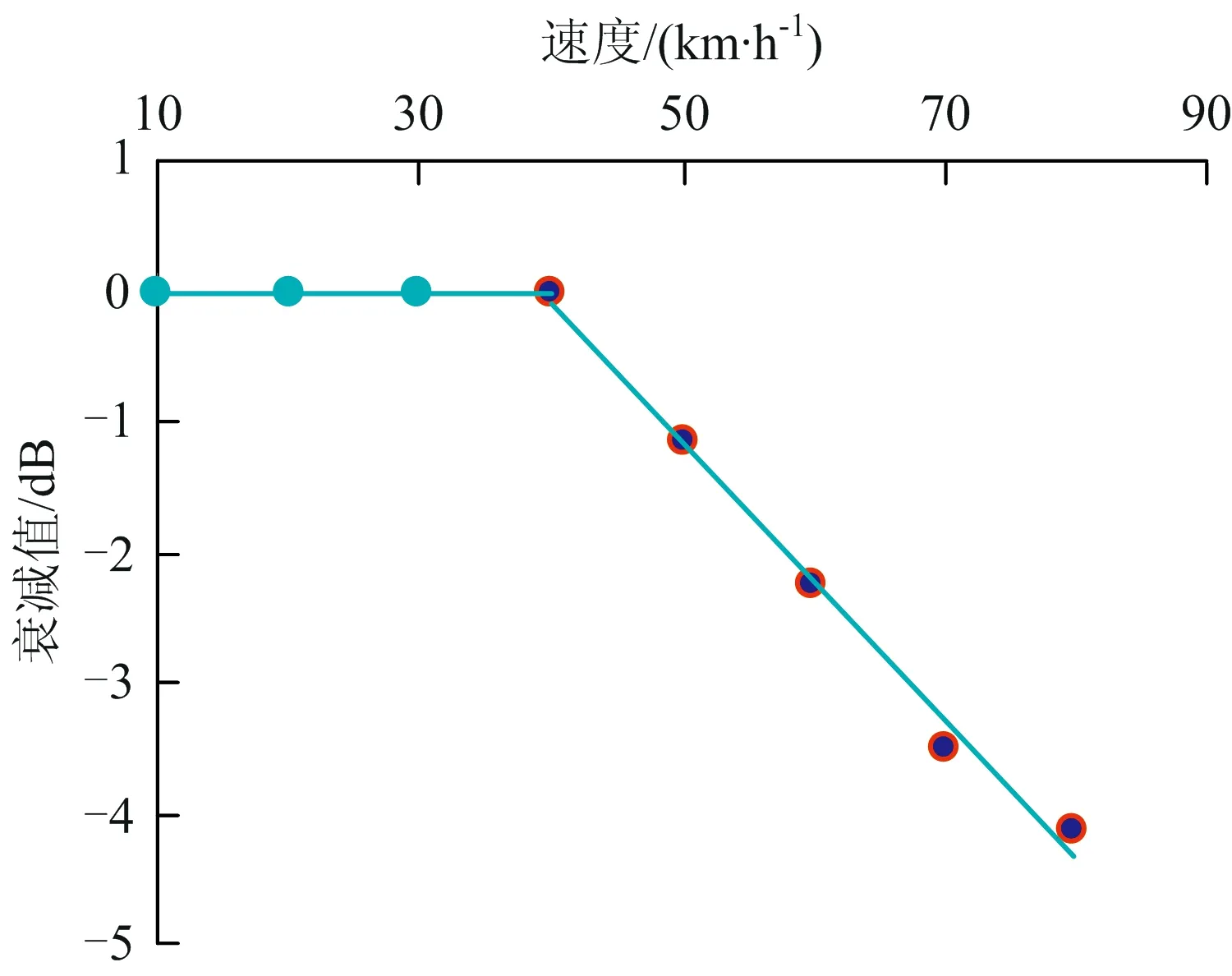
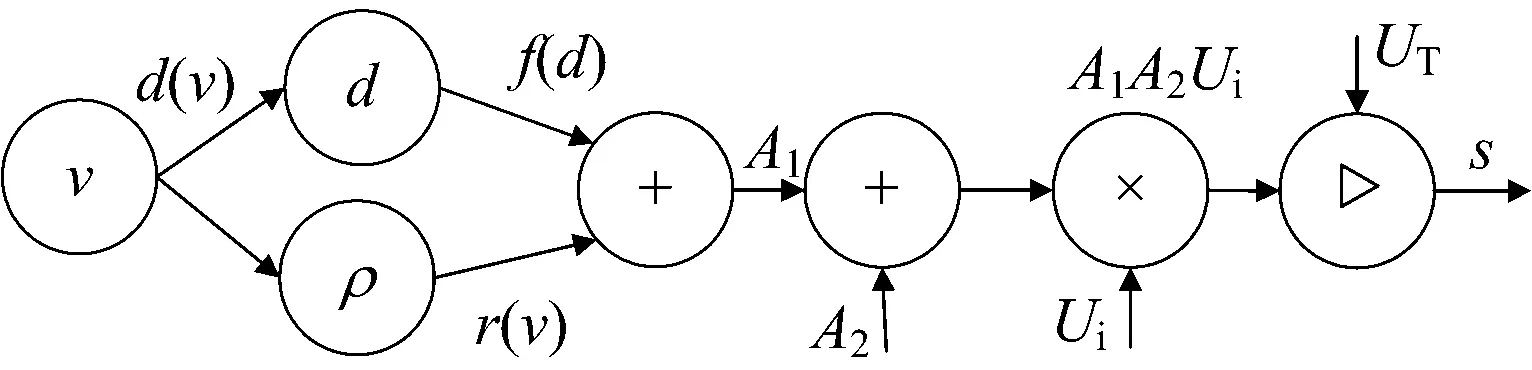
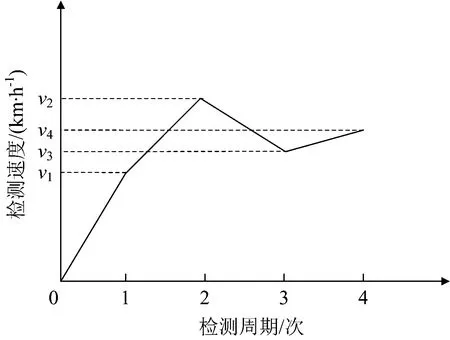
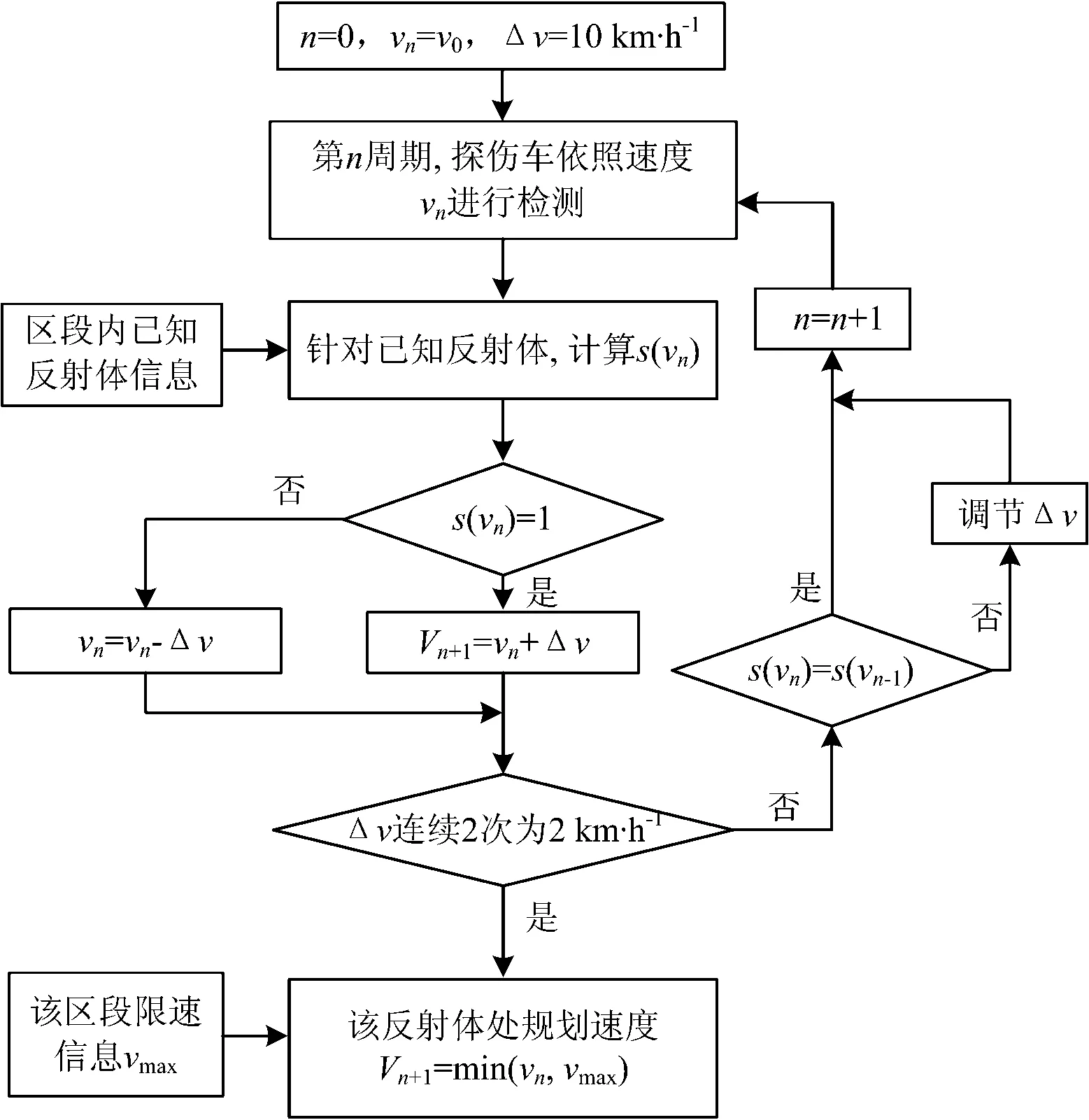
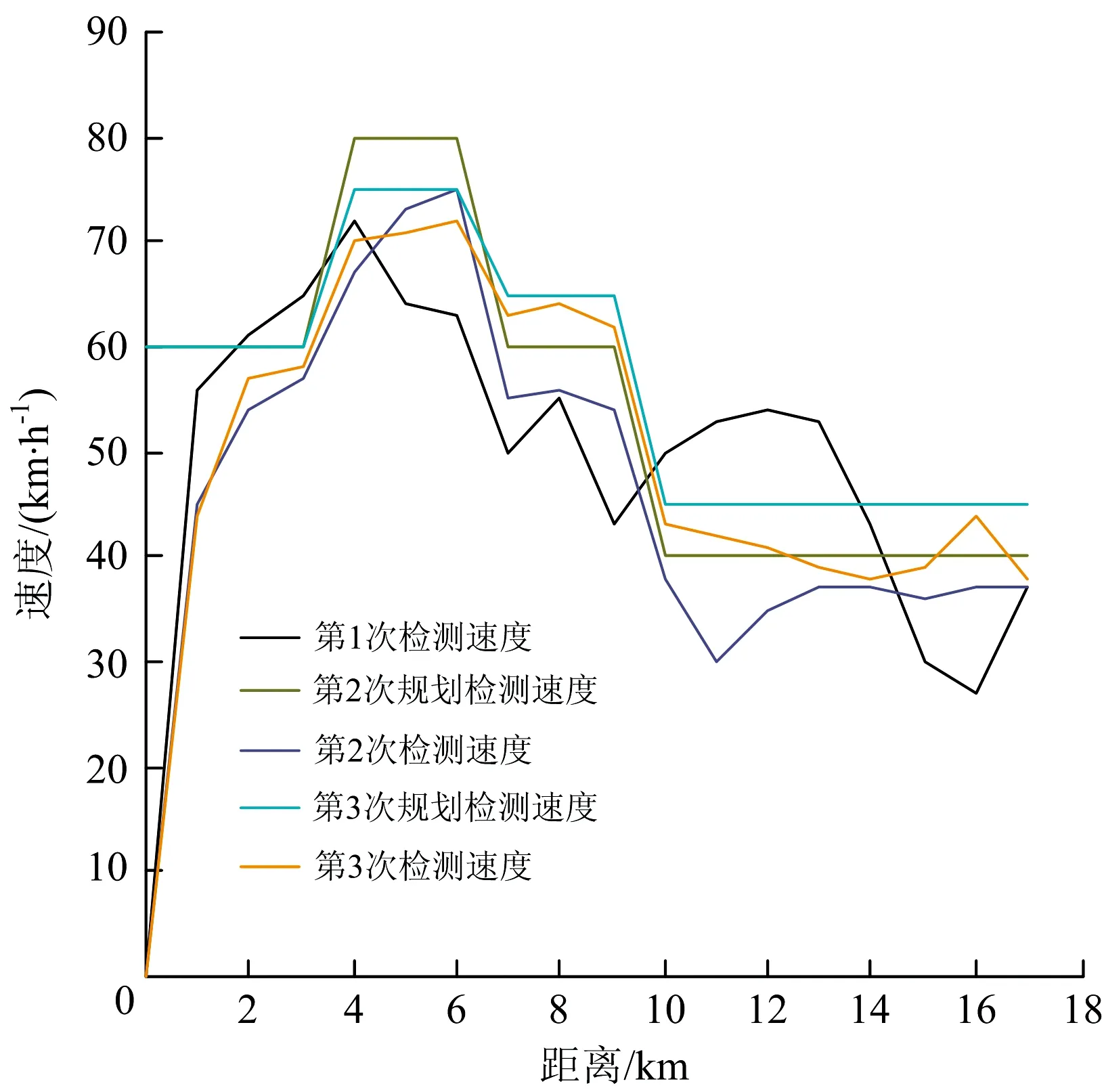
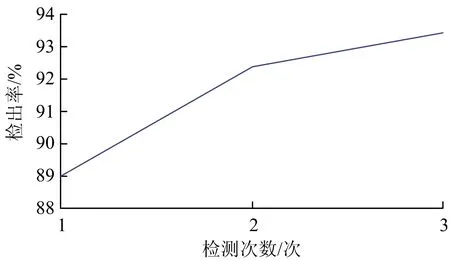
探伤车检测钢轨内部超声波反射体时,超声波反射体反射的超声波传输途径及处理过程如图1所示。由图1可见,超声波反射体反射的超声波(超声回波)Ui,途径钢轨、钢轨与探轮界面、探轮液的衰减后变为A1Ui(A1为超声波在传播途径中的衰减),之后被超声波传感器接收,经放大器放大A2倍后放大为A1A2Ui,与阈值UT比较,比较结果为s; 当A1A2Ui≥UT时,s=1,表示超声波反射体被检出,当A1A2Ui 图1 超声波反射体反射的超声波传输及处理过程 即 (1) 式(1)中,A2和UT为操作员在检测过程中设置的参数,因此影响超声波能量传播的因素有2个:探轮对中偏差d和喷水密度ρ,则 A1=f(d)+r(ρ) (2) 式中:f(d)为探轮对中偏差d引起的超声波衰减;r(ρ)为喷水密度ρ引起的超声波衰减。 在试验室静态条件下,可通过探轮标定架测量d及f(d)。静态条件下,耦合水可充分浸润钢轨表面的微观结构,排出其中的空气,因此喷水密度ρ引起的超声波衰减可忽略。探轮及钢轨试块安装在探轮标定架上,探轮相对钢轨试块静止。安装探轮及钢轨试块的探轮标定架如图2所示。将探轮上的0°超声波传感器与超声波探伤仪连接,超声波探伤仪的衰减读数即为探轮在预设的对中偏差下的超声波衰减。 调节探轮横向位置,使探轮中的0°超声波与钢轨轨腰对齐,0°超声波钢轨底波达到最高,此时探轮对中偏差记为0 mm,记录此时超声波探伤仪的读数f(0)。沿钢轨横向向内依次调节探轮对中偏差为1,2,…,8 mm,并逐个记录超声波探伤仪读数f(1),f(2), …,f(8)。沿钢轨横向向外依次调节探轮对中偏差为1,2,…,8 mm,并逐个记录超声波探伤仪衰减读数f(-1),f(-2), …,f(-8)。将探轮对中偏差作为横轴,将f(0)-f(d)(d=-8, -7, …, 7, 8)作为纵轴,描点后使用二次曲线对f(d)进行拟合,测试数据及拟合曲线如图3所示,拟合曲线的表达式为 图2 安装有探轮及钢轨试块的探轮标定架 f(d)=-0.315 7d2-0.065 44d-1.477 (3) 喷水密度ρ为填充入钢轨表面微观结构的水量与钢轨表面微观结构的空间体积之比,即 (4) 式中:mr为单位时间内浸入空隙的水的质量;t为水浸入空隙的时间;V为钢轨表面微观结构的空间体积。 图3 超声波衰减函数f(d)的拟合曲线 当ρ=0时,即钢轨表面微观结构中全为空气,超声波衰减系数为空气中衰减系数B气,当ρ=ρ水时,即钢轨表面微观结构中充满水,超声波衰减系数为水中衰减系数B水,因B水≪B气,则B水可忽略不计。故 r(ρ)=-B气ρ+B气 (5) 式(4)中的水浸入空隙的时间t与探伤车检测速度v间的关系为 (6) 式中:L为喷水嘴位置距离0°超声波传感器的位置之间的距离。 将式(6)代入式(4),可得喷水密度ρ与检测速度v之间的关系为 (7) 将式(7)代入式(5)可得检测速度通过影响喷水密度变化引起的超声波衰减r(v)为 (8) 当钢轨表面状态一定时,式(8)中B气,mr,V和L等参数均可认为是常数,当探伤车检测速度v变大时,r(v)变小,为简单起见,用线性函数拟合式(8),在平直线路上进行试验以拟合式(8)中各个常数。 选择平直线路上长度为3 mm的螺孔水平裂纹作为超声波反射体,分别以10,20,…,80 km·h-1的检测速度对其进行检测,各检测速度对应的超声波衰减记为r(10),r(20), …,r(80)。 以r(10)作为基准值,计算衰减值r(10)-r(v)(v=10, 20, …, 80)。由衰减值发现,在速度v≤40 km·h-1时,衰减值几乎未发生变化,当速度v>40 km·h-1时,r(v)近似为线性函数,随着速度v的增大r(v)的绝对值增大。以速度v为横轴,以r(10)-r(v)(v=10, 20, …, 80)值为纵轴,描点后进行分段拟合,结果如图4所示。 图4 检测速度通过喷水密度引起的超声波衰减值 拟合曲线的表达式为 (9) 检测速度v对探轮对中偏差d的影响d(v)与实际检测线路的曲线半径、钢轨磨耗、线路平顺性等多种因素密切相关,不同的线路d(v)不同,但线路在一定时间内该参数是固定不变的。探伤车的探轮对中系统可自动记录检测过程中每一个位置的检测速度与探轮对中偏差,因此该数据可通过实际检测过程中获得,并被记录下来。 经过上述分析,超声波反射体动态检出效果模型(简称v-s模型)如图5所示。图中:▷表示Uo与UT进行比较。 图5 v-s模型 在v-s模型中,对某一线路的某个位置,采用相同的车辆设备进行检测,速度v与探轮对中偏差d的关系可认为是一一对应关系。因此,对某条线路中的单个超声波反射体,可建立v-s模型。 基于动态步长调节法的检测速度规划原理如图6所示。 图6 基于动态步长调节法的检测速度规划原理 由图6可见:在第1次检测周期中,检测速度为v1,检测完成后,分析超声波反射体的检测结果s(v1), 若s(v1)=1,超声波反射体可完全检出,则对第2次检测周期的检测速度提速到v2=v1+Δv,当第2次检测周期完成后,若s(v2)=1,可继续提速,若s(v2)=0,超声波反射体无法检出,则降速到v3=v2-Δv,若第3次检测周期完成后,s(v3)=1,超声波反射体可检出,则提速到v4=v3+Δv。检测速度规划的速度步长Δv逐渐变小,目前速度步长设置为4档,步长由第1档至第4档逐渐减小,分别为10,5,3,2 km·h-1。 当s(vn)≠s(vn+1)时,步长Δv逐次减小,当Δv降至2 km·h-1时,步长不再变化。当动态步长连续2次为2 km·h-1时,速度规划停止,取较低的速度值为规划速度。经过若干次检测周期后,可得出收敛的该超声波反射体处的规划检测速度。 采用v-s模型对单个超声波反射体处进行速度规划流程如图7所示。图7中,n为检测周期的次数,在第n次检测周期时,探伤车依照速度vn进行检测,检测完成后可获得检测数据。 检测速度规划依据已知反射体进行计算,因此在每个反射体处均可规划出1个检测速度,对于特定的检测区间,将每个反射体处规划得到的检测速度用直线连接,可得到1条与探伤车检测线路里程相关的速度曲线,速度曲线代表的是特定检测区间的探伤车最大检测速度。 受检测区间的线路运行限速条件限制,探伤车的检测速度同时需满足检测区间内的运行限速要求,因此,规划的下次检测速度vn+1为 vn+1=min(vn,vmax) (10) 式中:vmax为检测区间的线路限速。 除此之外,线路中规划的检测加速度需满足探伤车加减速性能要求,因此速度曲线是连续的。 图7 探伤车检测速度规划流程 为验证基于动态步长调节法的探伤车检测速度规划方法的有效性,选取上海铁路局皖赣线某段16.16 km的线路区间作为被检测对象,该线路区间既有直线又有曲线,且为有缝线路,已知超声波反射体较多。在该区间共进行了3次检测,进行了2次检测速度规划。实际检测速度与规划检测速度如图8所示。 图8 各次检测时的实际检测速度曲线与规划检测速度曲线 由图8可见:在第1次检测时,由于没有可参考的规划检测速度,实际检测速度由探伤车司机随机控制,在第1次检测完成后,通过分析数据规划出了第2次检测时的规划检测速度曲线,发现在10~14 km区间内第1次检测速度超出了第2次检测的规划速度,故已知第1次检测时超声波反射体的检出率应低于第2次检测时的检出率。第3次检测时的规划检测速度略高于第2次检测规划速度,表明第3次检测规划后检出效率得到了提高,已知超声波反射体的检出率变化不大。 统计各次检测数据后已知超声波反射体的检出率如图9所示。由图9可见:第2次检测时已转超声波反射体检出率高于第1次检测时,第3次检测时已知超声波反射体检出率与第2次检测时相比变化不大,这与对图8的分析结论相符,表明探伤车在有缝线路上的检测速度规划方法可行。 图9 3次检测中已知反射体检出率 为对有缝线路上钢轨探伤车检测速度进行规划,在超声波反射体静态检出原理基础上,通过分析探轮对中偏差和喷水密度2个因素对超声波的衰减规律及检测速度对这2个因素的影响关系,建立了超声波反射体检出效果模型。基于动态步长调节法,设计了超声波反射体的检测速度规划方法,并通过对多次超声波反射体速度规划,并结合线路限速信息,得出反射体所在线路的下次检测时探伤车的规划速度。通过实际线路3次检测对比,验证了探伤车检测速度规划方法的有效性。
1.2 探轮对中偏差d引起的超声波衰减函数f(d)

1.3 喷水密度ρ引起的超声波衰减函数r(ρ)
1.4 检测速度v对喷水密度ρ的影响
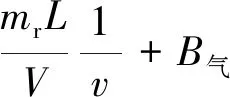
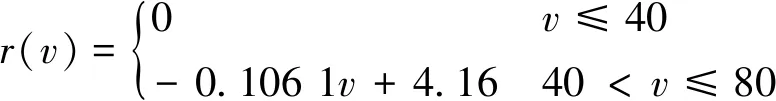
1.5 检测速度v对探轮对中偏差d的影响
1.6 超声波反射体动态检出效果模型
2 基于动态步长调节法的检测速度规划
3 试验验证
4 结 语
