大跨度斜拉桥—无砟轨道结构变形适应性研究

朱志辉，闫铭铭，李晓光，盛兴旺，郜永杰，喻泽红

(1. 中南大学 土木工程学院，湖南 长沙 410075； 2.中南大学 重载铁路工程结构教育部重点实验室，湖南 长沙 410075； 3.中铁第四勘察设计院集团有限公司，湖北 武汉 430063)

随着高速铁路的快速发展，无砟轨道得到广泛应用[1]。目前我国在中小跨度桥梁上铺设无砟轨道已有成熟的工程经验，但尚无大跨度斜拉桥铺设无砟轨道的先例，相关理论研究和工程经验不足，现有规范中对斜拉桥上无砟轨道变形的控制指标还不完善。与传统有砟轨道无缝线路相比，除关注钢轨纵向附加力外，无砟轨道结构和桥梁之间的变形适应性问题，包括轨道结构和桥面板的竖向变形曲率、无砟轨道层间压缩量和梁端转角等指标，对轨道结构工作性能和耐久性问题具有重要影响[2]。由于斜拉桥结构复杂，受温度、风以及列车荷载作用时主梁变形显著，而无砟轨道适应变形的能力较低[3]，因此无砟轨道结构与大跨度斜拉桥间的变形适应性问题亟待研究。

国内外学者对无缝线路轨道与桥梁相互作用问题已开展了较多研究[4-11]。DAI对比说明了连续梁桥上无砟轨道无缝线路采用小阻力扣件的优势。李永乐建立无砟轨道局部精细化模型，分析了钢桁梁斜拉桥上无砟轨道整体刚度特点。周敏研究了简支梁桥上纵连板式无砟轨道稳定性的影响因素。王平编制通用计算软件，研究了斜拉桥上有砟轨道无缝线路纵向力分布规律。P Ruge提出了有砟轨道考虑加载历史的梁轨非线性分析方法。上述研究多为简支梁、连续梁桥，研究指标多为钢轨应力、纵向位移等，较少涉及无砟轨道结构与大跨度斜拉桥间变形适应性问题。

针对上述情况，本文以某客运专线上拟铺设CRTSⅠ型双块式无砟轨道的某特大斜拉桥为研究对象，建立了无砟轨道—桥梁空间精细化非线性分析模型，采用非线性弹簧单元模拟扣件阻力、凸型挡台咬合力、隔离层摩擦阻力等。通过计算列车竖向荷载和温度荷载作用下轨道结构和桥面板的竖向变形曲率、无砟轨道层间压缩量及梁端转角，分析说明无砟轨道结构与大跨度斜拉桥间的变形适应性。

1 工程背景

某新建高速铁路客运专线上拟铺设CRTSⅠ型双块式无砟轨道的大跨度斜拉桥桥跨布置如图1所示，主桥采用(35+40+60+300+60+40+35)m双塔斜拉桥。其中，(35+40+60)m边跨主梁采用混凝土箱梁型式，梁顶宽16.5 m，高4.5 m；中跨主梁采用钢箱—混凝土板结合梁型式，梁顶宽16.3 m，高4.5 m。主桥及相邻简支梁桥上拟铺设CRTSⅠ型双块式无砟轨道，该桥建成后将是世界上首座设计时速350 km、铺设无砟轨道的大跨度混合梁斜拉桥。

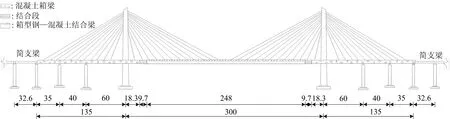
图1 大跨度斜拉桥桥跨布置图(单位：m)

CRTSⅠ型双块式无砟轨道是我国在引进、吸收德国Rheda2000无砟轨道系统的基础上，结合我国实际再创新的一种新型轨道结构，现已在我国武广、合福等客运专线中得到广泛应用。桥上CRTSⅠ型双块式无砟轨道为单元分块式结构，自上而下分别是钢轨、扣件系统、双块式轨枕、混凝土轨道板、隔离层、混凝土底座板。本文斜拉桥上CRTSⅠ型双块式无砟轨道结构横断面如图2所示，轨道板长、宽、高尺寸分别为5 920，2 800和260 mm，底座板与轨道板同长同宽，厚度为240 mm，单元板之间设有80 mm的板缝。每块轨道板底部两侧设有抗剪凸台，底座板对应位置设有限位凹槽(四周设橡胶垫板)，用以传递纵、横向荷载，同时限制轨道板和底座板间纵、横向相对位移。

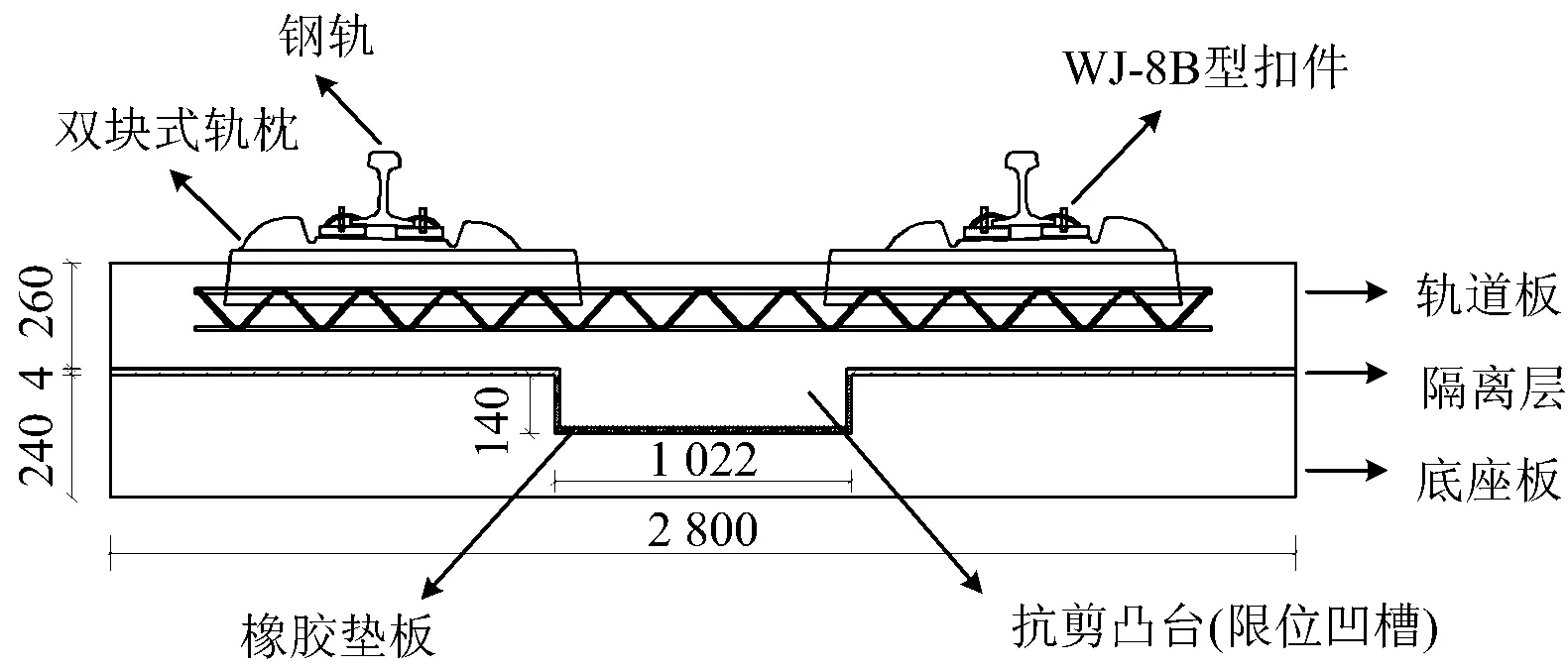
图2 CRTSⅠ型双块式无砟轨道横断面图(单位：mm)

2 无砟轨道—斜拉桥相互作用计算模型

2.1 无砟轨道—桥梁有限元模型

目前轨道—桥梁相互作用模型有梁单元模型[12]、壳单元模型[13]及实体单元模型[14]。文献[14]指出：梁单元桥梁模型不能很好地反映高速铁路箱梁的空间力学特性，计算挠曲力会产生较大的误差；采用三维实体单元模拟桥梁在建模效率和计算效率方面不能满足大跨度复杂桥梁的需要。

基于上述情况，本文建立如图3所示的无砟轨道—斜拉桥空间精细化有限元模型，为准确模拟边界条件及纵向力传递，主桥两端各增加3跨简支梁桥，桥梁范围外各建立200 m钢轨延长段。斜拉桥主梁和桥墩均采用壳单元，桥塔采用空间梁单元，斜拉索采用杆单元。钢轨采用空间梁单元，轨道板和底座板均采用壳单元模拟。轨道结构与桥梁一体化计算模型的关键在于各结构层间接触方式的模拟[7]，无砟轨道层间、轨道与桥梁之间连接均采用弹簧单元模拟。扣件纵向阻力采用非线性弹簧模拟，扣件垂向刚度采用线性弹簧模拟；隔离层纵向摩阻力和凸型挡台纵向咬合力采用非线性弹簧模拟，隔离层采用只受压不受拉的垂向非线性弹簧模拟，以反映轨道板与底座板之间的垂向约束关系；底座板与桥面板整浇为一体，采用刚性弹簧连接。

2.2 参数取值

斜拉桥主梁混凝土弹性模量为35.5 GN·m-2，线膨胀系数为1.0×10-5℃-1；结合梁中钢材弹性模量为206 GN·m-2，线膨胀系数为1.18×10-5℃-1；斜拉索弹性模量为190 GN·m-2，线膨胀系数为1.1×10-5℃-1；其他截面参数及材料特性均按设计图纸取值。

斜拉桥上CRTSⅠ型双块式无砟轨道采用60 kg·m-1钢轨，WJ-8B型小阻力扣件，扣件纵向阻力—位移关系如图4所示，弹塑性临界点位移为0.5 mm，扣件垂向刚度根据文献[5]取35 MN·m-1。轨道板与底座板间纵向阻力包括土工布隔离层的摩擦阻力以及凸型挡台的纵向咬合力两部分，根据文献[15]，土工布隔离层摩擦系数为0.7～0.8，转折点位移为0.5 mm，本文考虑最不利情况，取为0.7。凸型挡台四周橡胶垫板刚度根据文献[15]取为180 kN·mm-1，轨道板与底座板间纵向阻力r的计算式为

图3 无砟轨道—斜拉桥精细化有限元模型

(1)

式中：u为轨道板与底座板间的纵向相对位移，mm。

图4 小阻力扣件纵向阻力模型

相应的轨道板与底座板间纵向阻力模型如图5所示。

隔离层垂向离散为单向受压弹簧单元，其等效抗压刚度K为

(2)

图5 轨道板与底座板间纵向阻力模型

式中：E为土工布隔离层弹性模量，根据文献[16]取3.32 MN·m-2；Ae为单个弹簧单元连接处的从属面积，mm2；h为土工布隔离层厚度，m。

2.3 有限元模型验证

为验证本文模型的正确性，表1给出了本文模型和设计院MIDAS模型在列车竖向荷载作用下主跨跨中竖向变形和斜拉桥梁端转角的计算结果对比。计算跨中变形时，列车竖向荷载取ZK均布活载，主跨双线满布加载；计算梁端转角时采用ZK标准活载按梁端转角影响线进行最不利加载。图6为荷载作用下简支梁与斜拉桥边跨的梁端转角a1和a2示意图(由斜拉桥结构的对称性，本文仅研究左梁端转角)。从表1可以看出，2种模型的主跨跨中变形和梁端转角计算结果相对差分别为4.1%和3.1%，吻合良好。

表1 模型计算结果对比

注：相对差=(本文计算结果-设计院结果)/设计院结果。

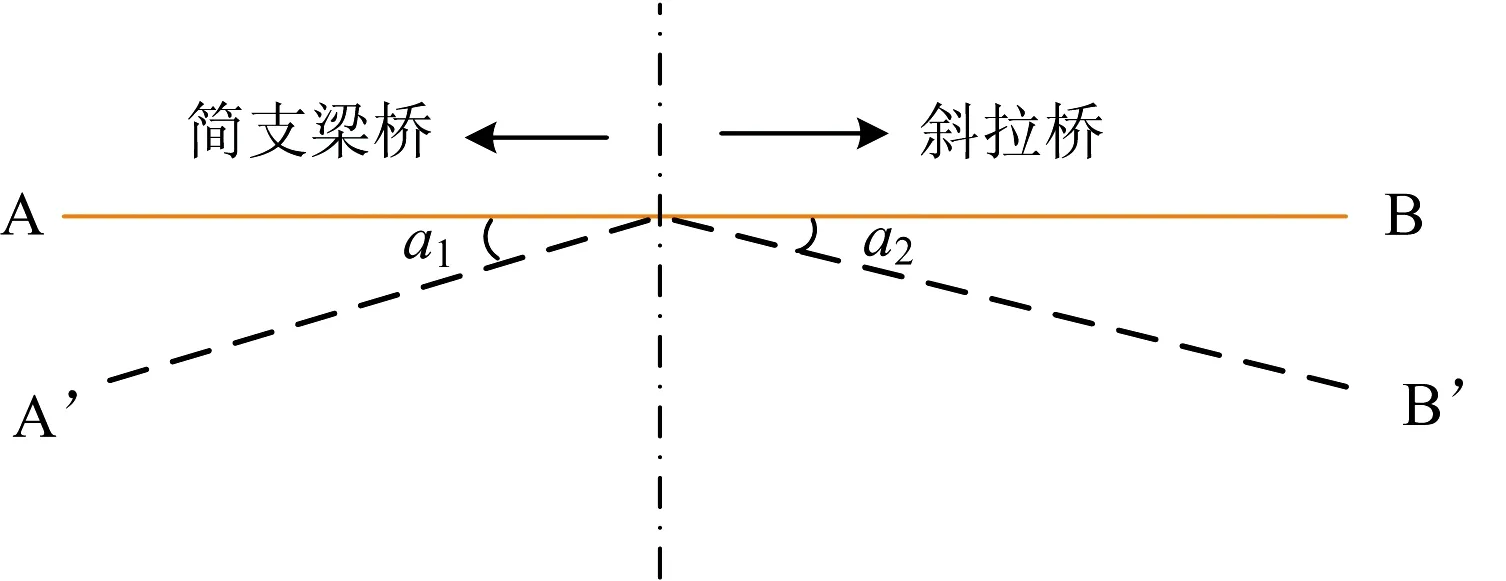
图6 梁端转角示意图

3 无砟轨道—大跨度斜拉桥变形适应性分析

为说明无砟轨道与大跨度斜拉桥之间的变形适应性，以成桥状态为计算初始状态，研究列车竖向荷载和温度荷载作用下轨道结构和桥面板的竖向变形曲率、无砟轨道层间压缩量及梁端转角。其中，列车竖向荷载采用ZK均布活载，根据计算指标按最不利位置加载；温度荷载以24 ℃为基准温度，考虑整体升、降温25 ℃。

3.1 竖向变形曲率

根据微积分中曲率求解公式，竖向变形曲率ρ的计算式为

(3)

式中：y是竖向变形，m。

本文规定结构向下的竖向变形为正值，因此，

当结构发生下挠变形时，曲率为正值；当结构发生上拱变形时，曲率为负值。

3.1.1 列车竖向荷载作用

列车竖向荷载作用位置不同引起的轨道—桥梁相互作用不同。为考虑列车竖向荷载的最不利加载位置，根据斜拉桥的对称性分别按图7中4种典型布载方式进行加载：布载1，主跨双线满布加载；布载2，左侧混凝土边跨+主跨双线满布加载；布载3，左侧混凝土边跨+主跨左半跨双线满布加载；布载4，左侧混凝土边跨双线满布加载。

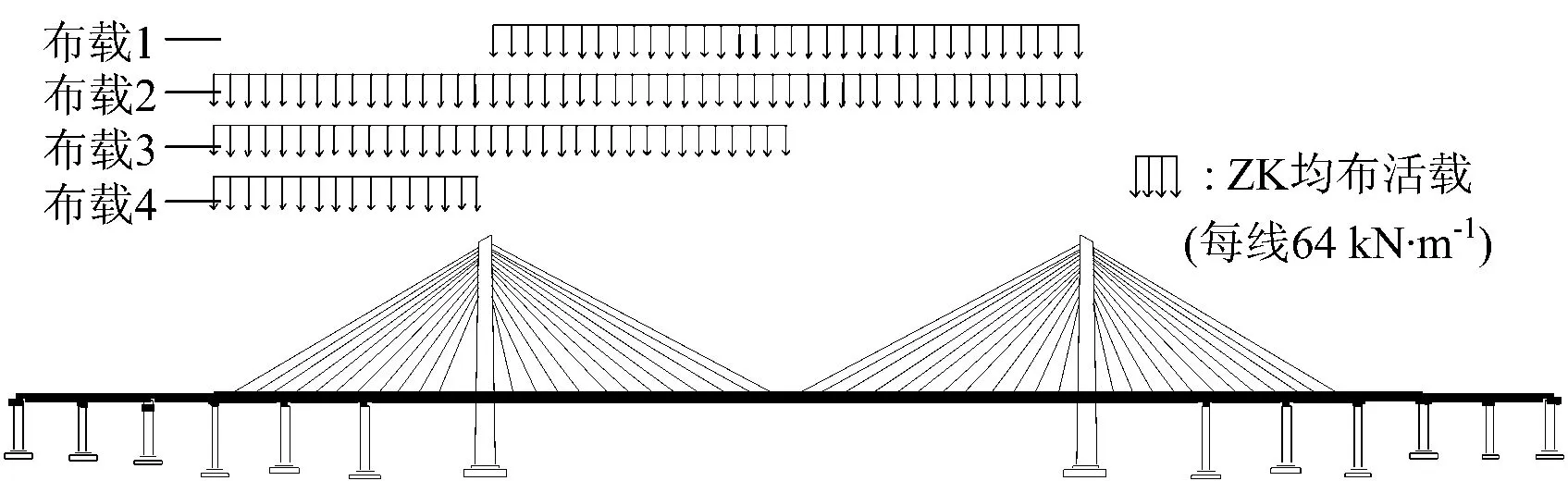
图7 列车4种典型竖向荷载布载方式

表2给出了不同布载方式下钢轨、轨道板和桥面板的最大曲率绝对值。从表2可以看出，布载1的钢轨、轨道板和桥面板曲率最大；布载4远小于其他3种布载方式，说明列车竖向荷载在斜拉桥中跨加载对各构件竖向变形曲率影响较大。

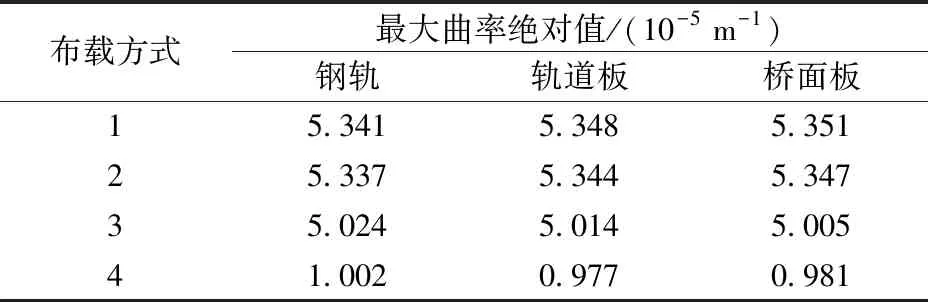
表2 不同布载方式下最大曲率绝对值

图8给出了列车竖向荷载按布载1加载时轨道结构和桥面板竖向变形曲率分布图。

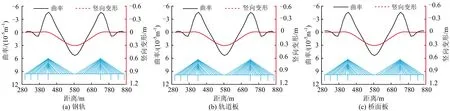
图8 竖向荷载按布载1加载时轨道结构和桥面板曲率分布

从图8可以看出列车竖向荷载在中跨双线加载时的以下几个结论。

(1)钢轨、轨道板和桥面板竖向变形曲率的分布规律相同、数值相近，表明钢轨和轨道板的曲率受扣件和土工布隔离层弹性变形的影响较小，主要受桥梁竖向变形影响。

(2)由于荷载和结构自身的对称性，曲率呈正对称分布，在中跨跨中、桥塔和临近桥塔的辅助墩等位置出现极值。钢轨、轨道板和桥面板的最大下挠变形曲率发生在中跨跨中位置，分别为5.341×10-5，5.348×10-5和5.351×10-5m-1；在桥塔处，各构件达到上拱变形曲率最大值，钢轨、轨道板和桥面板的最大上拱变形曲率分别为4.597×10-5，4.596×10-5和4.593×10-5m-1。

(3)按布载1加载时，桥梁以竖向变形为主，整体变形曲线较为和缓，桥面板最大竖向变形分别为0.307 m，对应的挠跨比为1/977。下挠曲率和上拱曲率较为接近，由于较大的曲率会引起无砟轨道附加弯矩，因此，除挠曲变形较大的跨中位置外，桥塔处无砟轨道的受力也应重点关注。

3.1.2 温度荷载作用

图9和图10分别给出了整体升、降温25 ℃时各构件的竖向变形曲率分布。从图9和图10中可以看出：整体升温和整体降温作用对各构件竖向变形曲率的影响大小相等、方向相反，因此下文仅讨论升温工况下各构件曲率分布。

(1) 与列车竖向荷载加载工况相比，升温工况下各构件曲率数值较小，分布更为复杂。各构件曲率除在跨中和桥塔位置出现极值外，在边跨和结合段内也有多处出现极值。

(2)升温工况下，钢轨、轨道板和桥面板在中跨跨中达到下挠变形曲率最大值，最大下挠曲率分别为9.547×10-6，9.539×10-6和9.541×10-6m-1；在桥塔向内侧45 m处，各构件上拱变形曲率达到最大值，钢轨、轨道板和桥面板的最大上拱曲率分别为1.725×10-5，1.734×10-5和1.728×10-5m-1。

(3)温度作用对各构件竖向变形均有较大影响，各构件竖向变形整体呈现多波性，除中跨发生长波大变形外，在35 m边跨和结合段内局部变形显著。

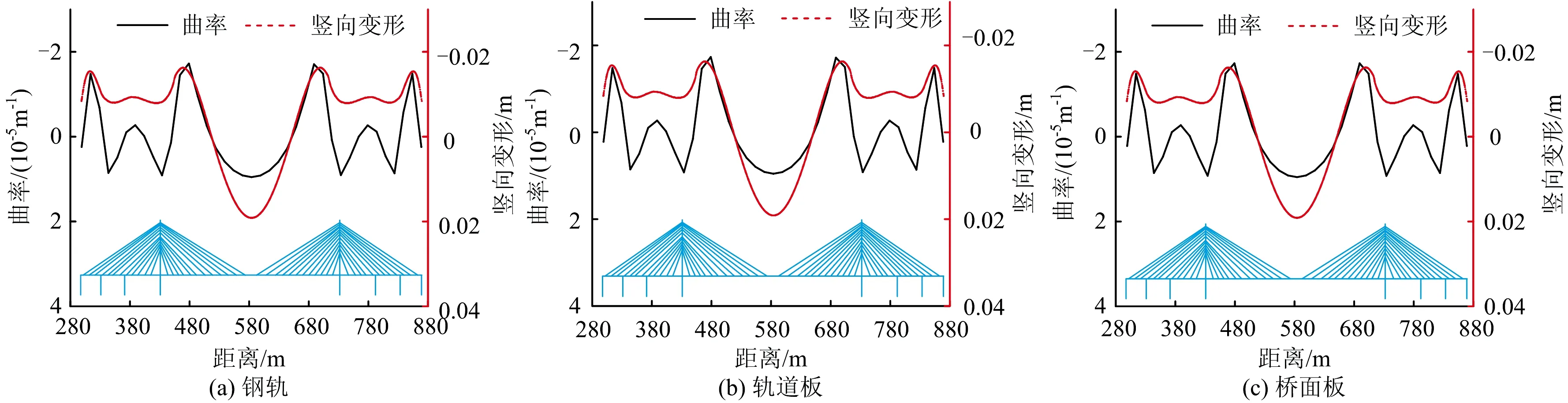
图9 整体升温时轨道结构和桥面板曲率分布

图10 整体降温时轨道结构和桥面板曲率分布

3.1.3 耦合作用

考虑列车竖向荷载与升温耦合、列车竖向荷载与降温耦合作用2种工况，其中，列车竖向荷载按图7所示的布载1进行加载，温度荷载按整体升、降温25 ℃计算。图11和图12分别给出了升温耦合、降温耦合工况下各构件竖向变形曲率分布。从图11和图12中可以看出：

(1)降温耦合工况下各构件上拱变形曲率在桥塔处急剧增大，而升温耦合工况下各构件上拱变形曲率在桥塔处较小。这是由降温作用和列车竖向荷载作用在桥塔处引起构件上拱变形叠加导致。

(2)升温耦合工况下，各构件下挠变形曲率较大，钢轨、轨道板和桥面板的最大下挠变形曲率分别为6.299×10-5，6.306×10-5和6.309×10-5m-1；降温耦合工况下，各构件上拱变形曲率较大，钢轨、轨道板和桥面板的最大上拱变形曲率分别为5.517×10-5，5.528×10-5和5.524×10-5m-1。

(3)耦合工况中列车竖向荷载对各构件竖向变形的整体分布影响较大，而各构件的局部变形(如梁端、桥塔等位置)受温度作用影响显著。

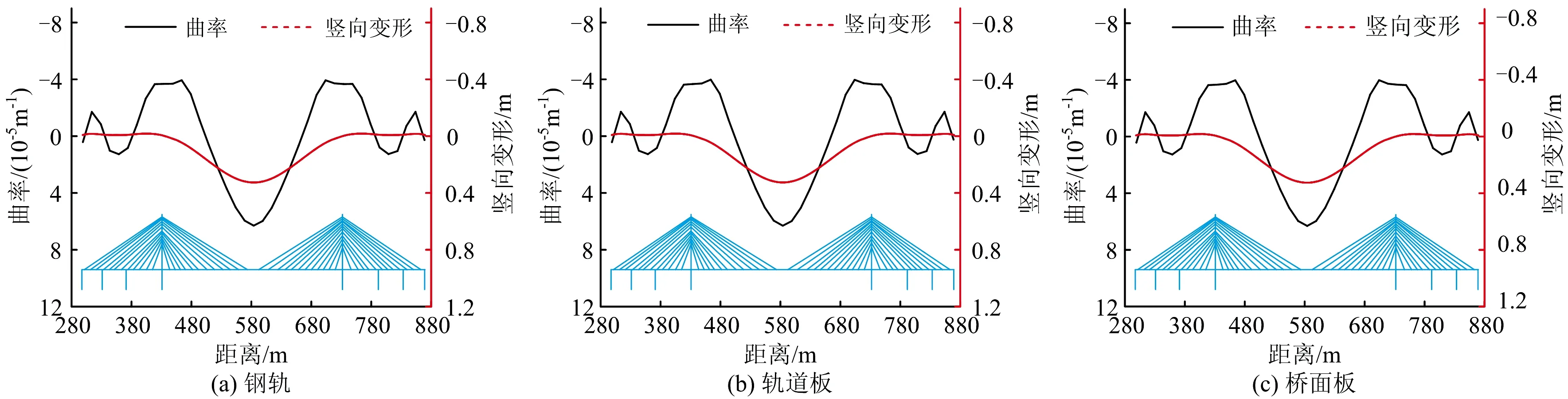
图11 升温耦合工况下轨道结构和桥面板曲率分布

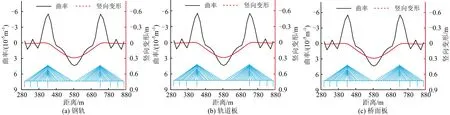
图12 降温耦合工况下轨道结构和桥面板曲率分布

3.2 无砟轨道层间压缩量

CRTSⅠ型双块式无砟轨道结构中轨道板与底座板之间设置有土工布隔离层，隔离层竖向仅受压不受拉。文献[3]对轨道板与桥面间协调变形性能进行分析时，未计入轨道板自重，出现了边支点与桥面脱离的现象。本文为更贴近实际工作状态，在计算竖向荷载和温度荷载作用下轨道结构层间压缩量时，考虑轨道结构自重引起的初始压缩量影响。

表3给出了6种荷载工况对应的荷载组合方式，以及各工况下轨道结构最大、最小层间压缩量，图13给出了各工况下无砟轨道层间压缩量分布。

表3 不同工况下最大、最小层间压缩量

注：层间压缩量为正值表示隔离层受压，为负值表示脱空。

结合表3和图13可以看出：

(1)6种荷载工况下无砟轨道层间基本处于受压状态，一般在桥塔和结合段等位置层间压缩量出现极值。其中，工况6的列车竖向荷载和降温耦合作用下层间压缩量最大，为0.108 mm。

(2)由于整体升温、整体降温作用引起梁端产生较大变形，致使梁端处层间压缩量增大。由于降温作用下中跨产生较大上拱变形，导致降温工况下中跨无砟轨道层间压缩量较小。温度作用下无砟轨道在结合段位置出现局部层间脱空现象，层间脱空最大值仅为0.021 mm。

3.3 斜拉桥梁端转角

斜拉桥在荷载作用下梁端转角过大会影响高速行车的安全性和舒适性。本节计算了列车竖向荷载和温度荷载作用下梁端转角，工况见表4。其中，竖向荷载按照梁端转角影响线进行最不利加载，图14给出了斜拉桥左梁端转角影响线和不同工况中竖向荷载的布载示意图。

梁端转角计算结果见表4，其中《高速铁路设计规范》限值一列中a为每孔梁的转角限值，b为转角之和限值。从表4可以看出，5种计算工况下梁端转角未超过规范限值，且有较高的安全富余度；其中，整体升温时主桥梁端转角最大，为1.049‰rad。

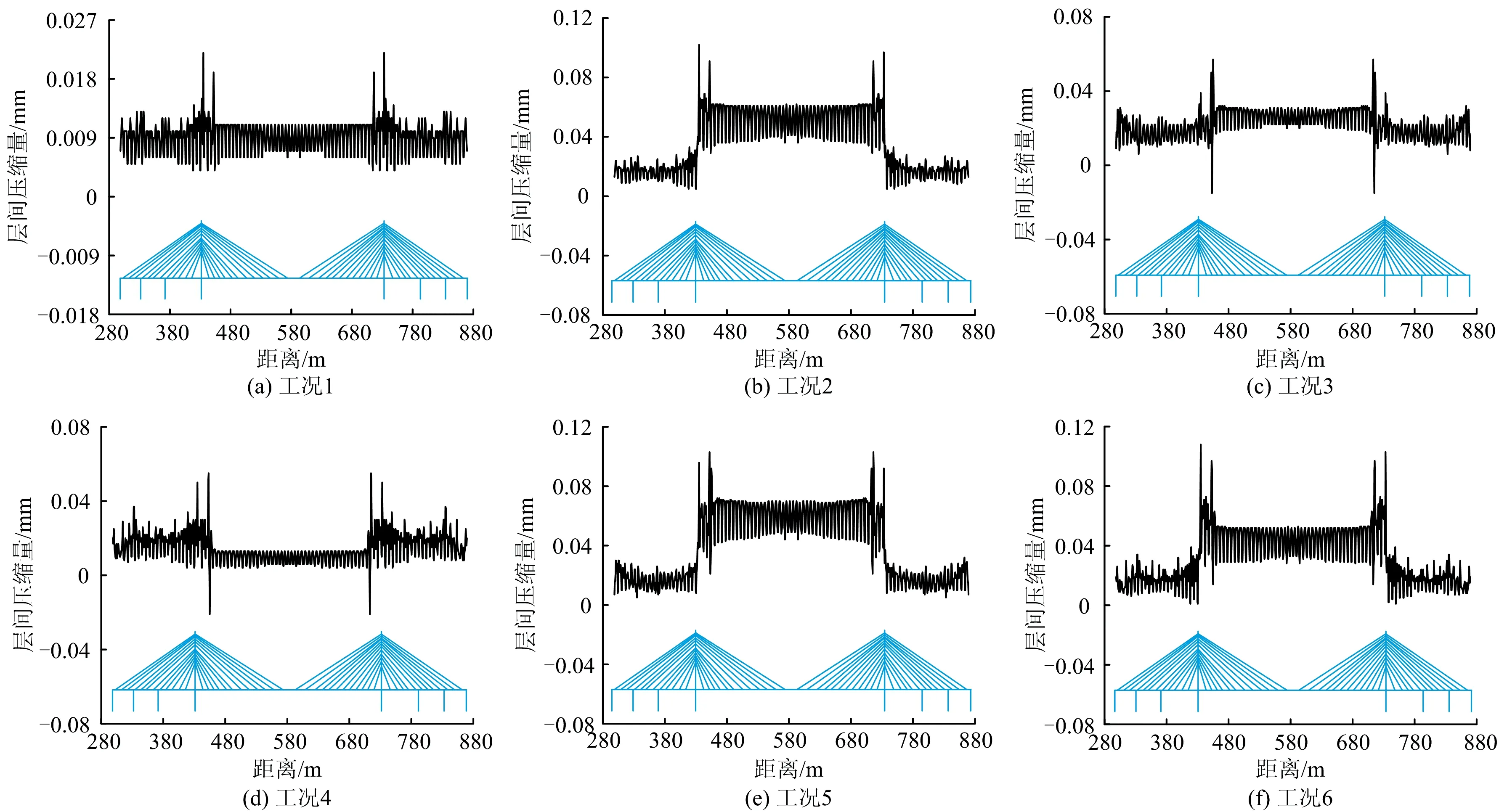
图13 不同计算工况下轨道结构层间压缩量分布

工况序号荷载组合a1/(‰rad)a2/(‰rad)a1+a2/(‰rad)《高速铁路设计规范》限值a/(‰rad)b/(‰rad)3整体升温25 ℃-0.106-1.049-1.1551.53.04整体降温25 ℃0.1021.0481.1501.53.07列车竖向荷载(布载见图14)0.2610.1290.3901.53.08列车竖向荷载(布载见图14)+整体升温25 ℃0.162-0.912-0.7501.53.09列车竖向荷载(布载见图14)+整体降温25 ℃0.1050.9801.0851.53.0

注：以桥梁下挠时梁端转角为正值，上拱时梁端转角为负值。

图14 不同工况列车竖向荷载布载示意图

4 结 论

(1)列车竖向荷载在斜拉桥中跨加载时对各构件竖向变形曲率影响较大；同一工况下轨道结构和桥面板竖向变形曲率的分布规律相同、数值大小相近；相比于列车竖向荷载，温度荷载作用下各构件竖向变形曲率分布更为复杂，但数值较小。

(2)列车竖向荷载与整体升温耦合作用下，各构件下挠变形曲率最大，钢轨、轨道板和桥面板的最大下挠变形曲率分别为6.299×10-5，6.306×10-5和6.309×10-5m-1；列车竖向荷载与整体降温耦合作用下，各构件上拱变形曲率最大，钢轨、轨道板、桥面板的最大上拱曲率分别为5.517×10-5，5.528×10-5和5.524×10-5m-1。

(3)除整体升温、整体降温作用下结合段处无砟轨道出现局部层间脱空外，荷载作用下无砟轨道层间基本处于受压状态，一般在桥塔和结合段等位置层间压缩量出现极值。

(4)主桥及相邻简支梁桥的梁端转角均未超过TB 10621—2015《高速铁路设计规范》中的限值，有较高安全富余度。