基于自适应模糊滑模的列车精确停车制动控制算法

何之煜，杨志杰，吕旌阳

(1.中国铁道科学研究院 研究生部，北京 100081； 2.中国铁道科学研究院集团有限公司 通信信号研究所，北京 100081； 3.北京邮电大学 信息通信学院，北京 100876)

列车自动驾驶(Automatic Train Operation，ATO)系统的作用是根据线路情况、行车许可、限速条件等因素自动生成行车曲线，并自动产生牵引/制动请求[1-3]。精确停车是ATO系统的关键技术之一，精度通常要求保证在30 cm之内。若停车不准，不仅会影响旅客上下车，而且会影响列车运营效率，甚至造成列车晚点等后果。随着我国高速铁路的快速发展，研究高速铁路ATO系统的精确停车算法具有重要意义[4]。

文献[5]通过分析城轨列车制动系统的构成、特性，提出了适用于控制器设计的制动模型。文献[6]设计了一种基于Krasovskii泛函算子的反推自动停车控制器，消除了制动过程中由于模型非线性和系统时滞带来的影响。文献[7]提出基于优秀司机经验的预测模糊控制算法，使列车在满足舒适性、准点率的条件下精确停车，但是没有考虑列车实际运行中外部非线性扰动的影响。实际上，在列车制动过程中，闸瓦摩擦系数变化的非线性和制动系统的动态特性将影响列车的停车精度。因此，文献[8—9]引入自适应控制，充分考虑系统参数模型和外部扰动的不确定性，增强控制系统的鲁棒性和适应性，实现列车高精度的跟踪。文献[10]根据城轨列车的制动特性，提出了2个简化的停车误差估计模型，并给出模型参数在线学习算法来抑制停车过程中外部的非线性扰动，但是在简化模型中由于忽略了空气阻力、坡度的影响，在实际制动过程中并不适用。文献[11]运用广义预测控制理论，设计了一种带约束的多目标预测控制器，达到高精度的停车要求，但是控制输出的是离散手柄级位，在现代高速列车连续输出的控制器中并不适用。

滑模控制，因其对系统参数变化和外界干扰具有完全的鲁棒性，在控制系统中得到广泛的应用[12]。然而，滑模控制在处理不确定因素时会使系统产生抖振现象，这种高频抖振现象不仅会影响控制的准确性，还会导致系统震荡或失稳。因此，将模糊控制的思想引入滑模控制中，用基于专家经验的模糊逻辑柔化切换控制信号，从而削弱了抖振现象[13-14]。

列车在实际制动过程中，由于线路纵断面产生的附加阻力、列车运行产生的基本阻力、闸瓦摩擦系数的变化以及线路上的运行环境变化(横风、会车、天气变化等)导致列车运行受到的阻力呈强非线性特征，很难对阻力进行精确建模，现有的研究多是对这一参数进行近似线性化处理或经验模型处理，容易造成由于模型误差对列车控制的影响。本文将上述阻力视作控制器的外部随机扰动，无需对扰动进行建模，可减少对线路数据的获取，降低控制器的复杂度。通过对列车制动模型的分析，基于模糊滑模理论设计了一种具有自适应性的自动停车控制器，利用等效控制和切换控制实现对系统参数摄动和外部扰动的鲁棒性控制，根据滑模切换状态，用模糊推理方法柔化切换控制信号，有效地削弱滑模控制的抖振现象，实现对列车停车曲线的精确跟踪，保证了停车精度，并通过仿真验证了算法的有效性。

1 问题描述

1.1 列车动力学模型

为便于描述，通常将列车看作1个刚性质点，其理想状态下的动力学模型为

(1)

式中：x为列车运行距离，m；v为列车运行速度，m·s-1；m为列车总质量，t；γ为列车回转质量系数，通常取0.06；Fu(t)为列车输入牵引力或制动力，kN；Fb(v)为列车运行受到的基本阻力，包括车轮滚动阻力、机械阻力和空气阻力，kN；Fa(v)为线路纵断面引起的附加阻力，包括坡道附加阻力fs、曲线附加阻力fc以及隧道附加阻力ft，kN；a0，a1，a2为阻力系数；g为重力加速度，取9.8 m·s-2。

1.2 列车制动系统模型

列车制动系统是列车调控速度、进站停车或紧急情况下保证列车安全的关键设备。现有高速铁路制动系统主要是电空制动，通过调节电制动和空气制动的比例，实现列车的减速制动。由于制动系统中的电气结构、微制动控制单元(MBCU)以及电空阀响应时间延时等因素造成时滞现象，使列车制动过程可以近似地描述成工业生产中典型的1阶滞后模型[5]，其数学模型可以表示为

(2)

式中：t为列车运行时间；ak为制动控制器输出的制动加速度，是由ATO系统输入的制动指令Fu(t)产生；τ为车载制动系统时间常数；as为制动曲线设定的加速度；σ为传输时延。

由于列车运行受到基本阻力、附加阻力以及实际环境未知干扰的影响，导致产生具有强非线性特征的附加加速度Δa(t)，则列车加速度a(t)为

a(t)=ak(t)+Δa(t)

(3)

可见，列车制动过程就是由ATO系统控制器输出制动指令，经由控制单元等结构时滞，输出控制列车实际状态的动态过程。列车制动模型如图1所示，图中s为复变量。

图1 列车制动模型

为了后续控制器的设计，引入帕德逼近来近似式(2)中的时延函数。

(4)

其中，

式中：λ为关于传输时延σ的常数。

利用式(4)对式(2)进行拉普拉斯变换，可以得到

(5)

式中：Ak(s)和As(s)分别为ak(t)和as(t)的拉普拉斯变换形式。

为便于表达，将式(5)改写为时域关系表达式为

(6)

其中，

在列车制动进站过程中，当列车驶过停车点时，ATO系统输出制动指令，设定制动加速度，并由制动控制单元(BCU)调节电空制动比，但是由于上述控制系统传输的时滞性，列车实际输出制动状态在时间上存在一定的延迟，即列车运行与设定制动曲线存在一定的偏离，但是经过控制器的调整，列车可以快速收敛到制动曲线上，最终实现精确停车，如图2所示。然而，线路上存在强非线性干扰，如基本阻力、线路附加阻力以及未知环境阻力等，影响列车对制动曲线的精确跟踪。因此，本文的重点是仅依靠列车的状态信息，如何设计合理的列车制动控制器来补偿运行过程中非线性扰动的影响，也就是补偿式(3)中Δa(t)，从而控制列车精确跟踪参考制动曲线。

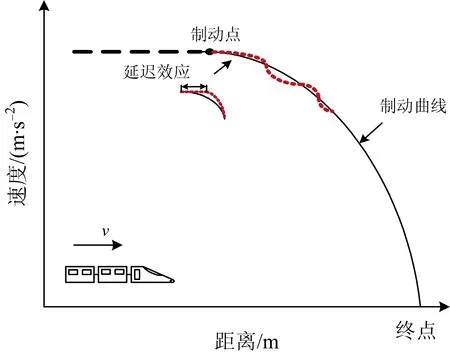
图2 列车制动过程

2 自适应模糊滑模控制器设计

滑模控制器具有很强的鲁棒性，能使控制系统在有限时间内收敛到滑模面，使收敛误差接近于零。通过引入模糊规则柔化切换控制，提高控制精度和跟踪精度，能使列车以较快的收敛速度逼近制动曲线，完成精确停车。

列车制动的模糊滑模控制原理如图3所示。

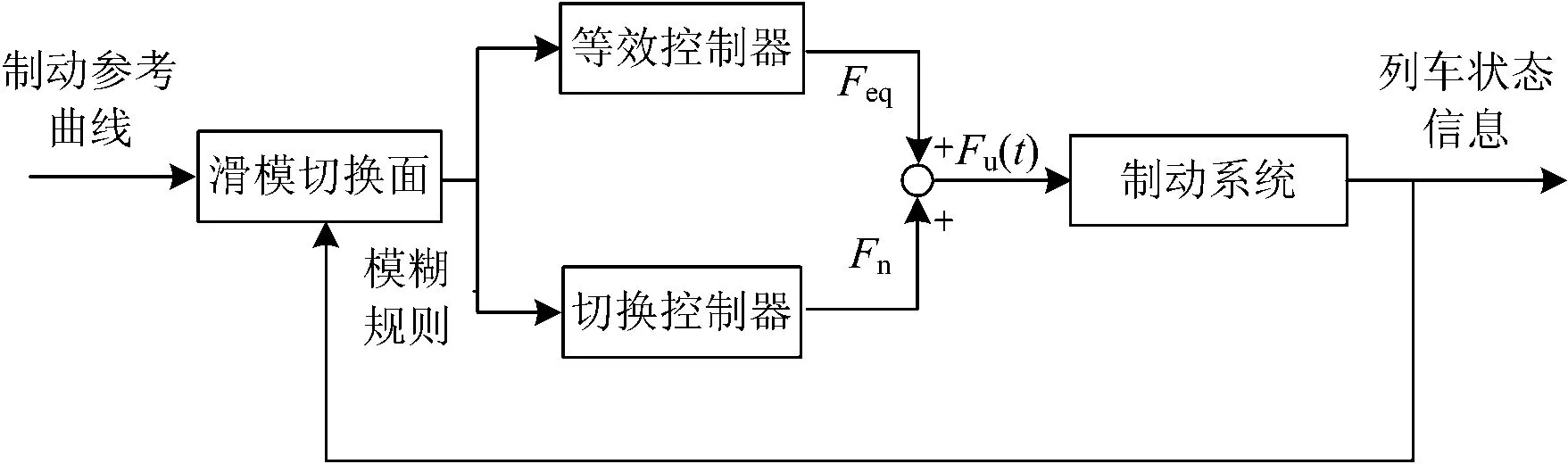
图3 列车制动的自适应模糊滑模控制原理

列车制动的自适应模糊滑模算法步骤如下。

(1)根据线路条件、列车运行情况等，生成列车参考制动曲线，并设定系统传输时延σ和系统时间常数τ。

(2)定义列车状态误差跟踪函数，并定义滑模切换面。

(3)设计模糊推理机，定义模糊规则以及去模糊化方法。

(4)根据切换函数sm，计算当前时刻的等效控制量Feq(t)。

(5)计算列车误差跟踪函数e1和e2，并作为模糊推理机的输入，得出切换增益，从而计算出当前时刻的切换控制量Fn(t)。

(6)计算制动控制器实际输出制动力Fu(t)。

(7)若列车运行速度不为零，返回步骤4，直到列车精确停车。

2.1 等效控制器

定义列车状态跟踪误差为

(7)

式中：e1为距离跟踪误差；x为列车位置；xd为参考位置；e2为速度跟踪误差；vd为参考速度。

对式(7)进行微分，可以得到新的列车状态跟踪误差为

(8)

式(8)中，假设Δa有界，且满足|Δa|≤Δamax(Δamax为附加加速度上界)，则定义误差向量e=(e1e2)，构造切换函数sm=cTe=c1e1+c2e2，常数c1和c2满足赫尔维茨多项式。

考虑列车运行中实际环境的非线性干扰，引入随机扰动参数FD(t)(单位kN)，结合式(1)，将式(3)改写为

(9)

由式(9)可得

(10)

式中：fb(v)，fa(v)，fd(t)分别为Fb(v)，Fa(v)，FD(t)的单位阻力参数，N·kN-1。

联立式(2)、式(6)和式(10)，可以得到列车制动控制器输出的制动加速度为

(11)

将式(7)和式(10)代入切换函数的1阶导数中，得

(12)

根据滑模控制原理，控制器输入Fu(t)为

Fu(t)=Feq+Fn

(13)

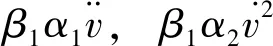
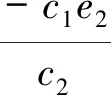
(14)

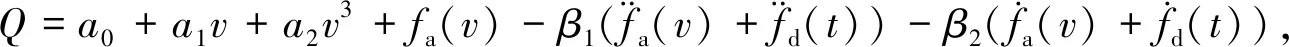
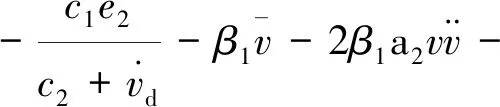
kwsgnsm

(15)

但是在实际过程中，列车运行中受到的阻力是未知的，因此，实际的等效控制器输入可以改写为

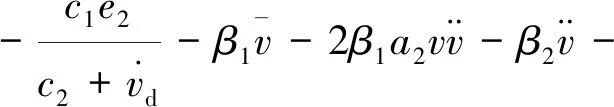
(16)

sm[-(kw-Q0)sgnsm-(Q0sgnsm-

(17)

式(17)说明该控制系统稳定，能较好克服外部干扰对控制器的影响，系统状态在滑模面上收敛于零。但是由于切换函数在滑模面上不连续的开关效应，采用切换控制容易产生抖振现象，为了满足控制系统的稳定性，需要设计具有动态自适应边界层范围的切换控制器。

2.2 基于模糊推理的切换控制器

在列车制动过程中，控制器切换律迫使系统不断穿过滑模面，由此产生的抖振现象不可避免，但是可以利用模糊规则柔化切换控制作用，控制列车实际制动曲线逐渐逼近参考制动曲线。

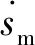
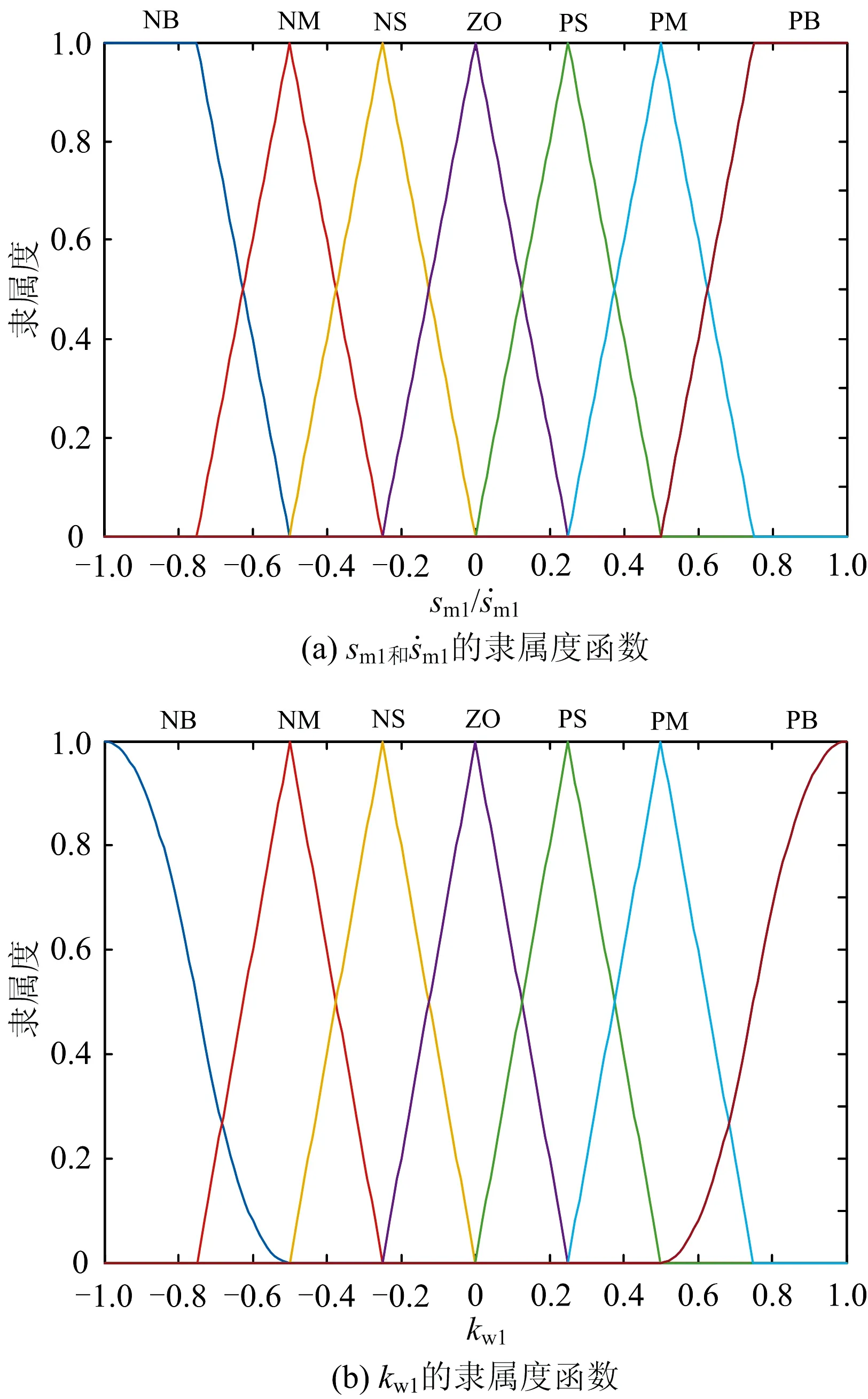
图4 模糊控制输入和输出量的隶属度函数

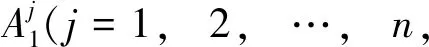
在模糊控制器的设计中，输入采用三角模糊化的隶属度函数设计，模糊推理过程采用乘积推理机，利用基于专家经验的模糊规则输出控制模糊语言值，最后去模糊化采用重心法得到精确控制量。

表1 模糊规则表

(18)

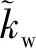
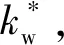
(19)

3 仿真分析

为了实现列车制动控制器对制动曲线的高精度跟踪，在面对列车运行阻力、线路纵断面附加阻力以及未知干扰时具有较好的适应性和鲁棒性，并综合考虑舒适度等因素，利用Matlab软件对所提出的自适应模糊滑模控制器进行仿真，并与传统的PID控制和基于指数趋近律的滑模控制(ISMC)进行对比、分析。

列车基本参数设置如下：列车满载重量为536 t，基本阻力表达式为fb=(0.42+0.0016v+0.000 132v2)(N·kN-1)，最大加速度设定为-0.9 m·s-2，ATO设定制动加速度为-0.6 m·s-2，质量回转系数为0.06，制动起始点位置设置为40 km处，制动时的初始速度设定为78 m·s-1，选取传输时延σ和系统时间常数τ分别为0.8和0.1 s。

列车在制动过程中，线路大多平缓，为了说明本文提出的制动控制算法的普适性，线路选取坡度较大的路段，如图5所示。

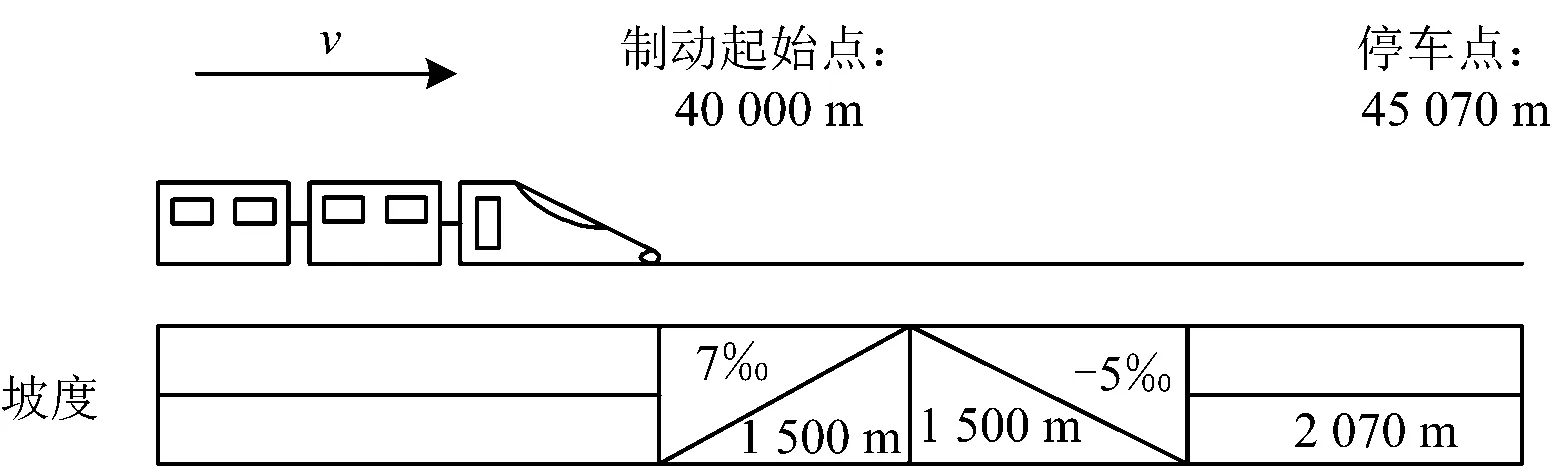
图5 列车制动线路参数

3.1 外部未知干扰为高斯白噪声时

由于列车测速测距设备、电气结构设备、传感器等不可避免地会产生随机误差，从而对观测结果造成扰动，这里综合地将这些扰动看作是高斯白噪声，即fd～N(μ,ζ2)。

传统的PID控制和ISMC与参考曲线的对比如图6所示。由图6可以看出：在制动曲线中，由于线路坡度和高斯白噪声干扰的影响下，2种控制曲线均在参考曲线上下波动，并且收敛速度较慢，最终PID控制的停车误差为55.3 cm，ISMC的停车误差37.5 cm，停车精度较差，均没有达到30 cm的精度要求；由列车运行的距离、速度以及加速度变化的对比可以看出，PID控制在距离和速度的误差上都比ISMC更大，而ISMC的加速度变化比较明显，在滑模面上下产生明显的抖振现象，影响列车运行舒适性。

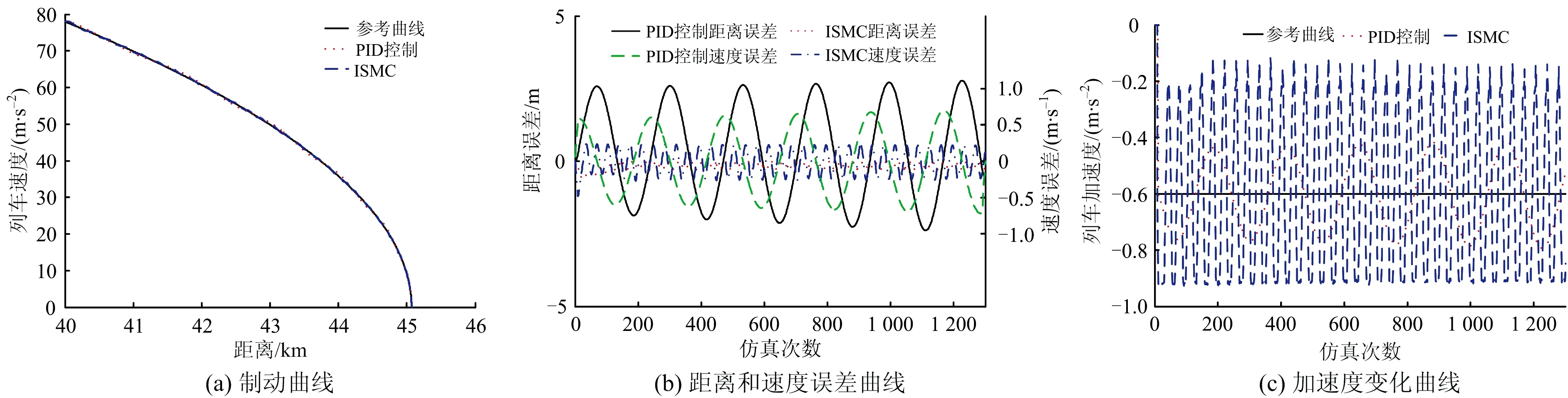
图6 PID控制和ISMC与参考曲线对比

本文提出的自适应模糊滑模控制(简称FSMC)与参考曲线的误差对比如图7所示。由图7可以看出：在线路阻力和位置阻力的作用下，控制器输出的制动曲线迅速收敛到滑模面，最终停车精度为18.9 cm，达到了小于30 cm的要求；并且列车制动控制加速度变化小，舒适性高，说明模糊滑模控制器具有较好适应性和鲁棒性。

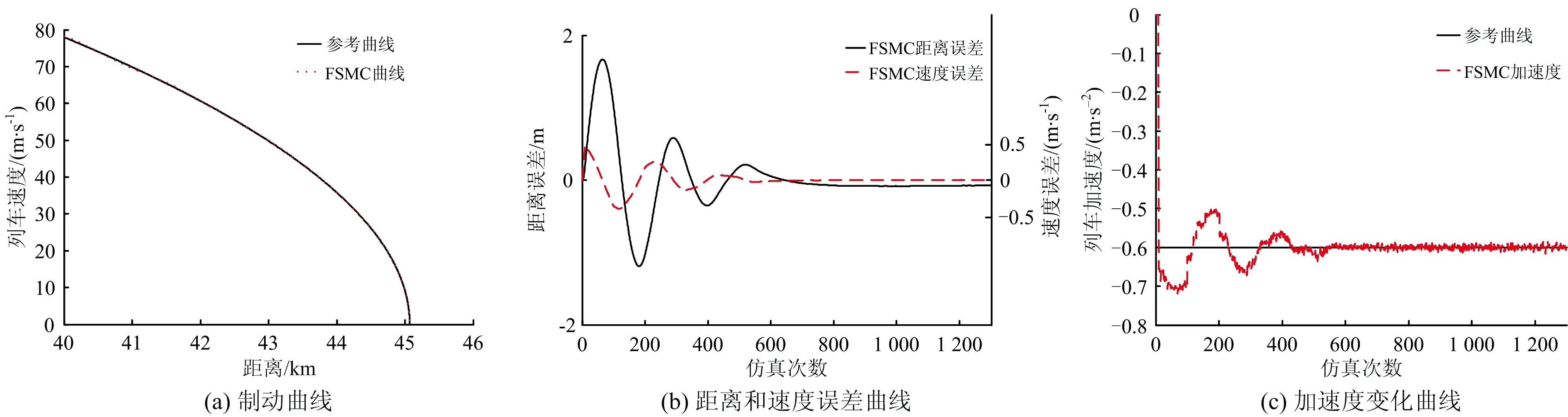
图7 FSMC与参考曲线对比

3.2 列车参数发生摄动时

随着列车运营里程的增加，列车制动系统及物理结构不可避免的出现磨损和老化，导致列车参数发生摄动，实际输出的制动力产生偏差，该变化属于慢时变过程。因此在每次列车制动停车过程的仿真中可将制动力偏差量视为恒定值；另外，依旧将外部未知干扰视作高斯白噪声。

列车实际输出制动力分别为总制动力的90%和80%时(即输出制动力产生10%和20%偏差)，输出曲线与参考曲线的对比如图8所示。由图8可以看出：列车由于受到制动系统损耗而输出90%和80%的实际制动力时，列车最终停车精度分别为17.3和18.6 cm，均满足30 cm之内的要求；制动系统参数偏差越大，列车的输出状态偏差也越大，收敛速度越慢，并且在切换面上的抖振越强烈，但是由于控制器的强鲁棒性和适应性，使系统状态能最终稳定在滑模面上，收敛于参考的制动曲线。

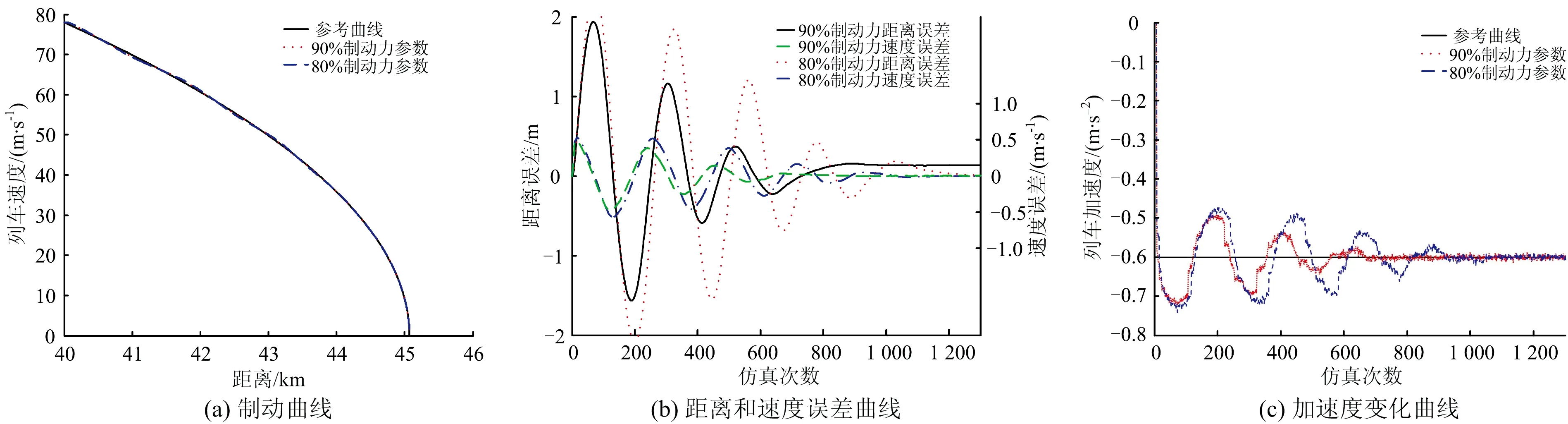
图8 制动力参数偏差下的输出曲线与参考曲线对比

4 结 论

(1)针对列车精确停车30 cm之内的要求，提出了自适应模糊滑模控制器，并充分考虑列车制动过程中所受到的强非线性扰动，设计出的控制器更能接近实际情况，符合系统的实用性。

(2)通过将非线性切换量模糊化，柔化了非线性切换控制量，削弱了滑模控制器的抖振现象，增强了控制器的适应性和鲁棒性。

(3)仿真平台对所提出的控制算法进行验证，在考虑附加阻力和未知干扰的情况下，模糊滑模控制器能使列车较快地收敛到参考制动曲线上，具有较高的停车精度，并与PID控制和基于指数趋近律的滑模控制算法进行了比较，验证了所提出算法的有效性。

(4)当输出制动力产生10%和20%偏差，以及存在附加阻力和未知干扰时，虽然列车输出状态在滑模面上产生较强烈的抖振，但是最终能使列车运行收敛到参考曲线上，并能达到精确停车30 cm之内的要求。