粉末涡轮盘夹杂缺陷的超声检出概率

， ，

(1.哈尔滨工业大学 先进焊接与连接国家重点实验室, 哈尔滨 150001；2.中国航发北京航空材料研究院检测中心, 北京 100095)

概率风险评估的一个必要输入是缺陷检出概率(Probability of Detection，POD)曲线。

目前关于无损检测可靠性的问题，最主要是研究某种特定的无损检测方法[1]，在特定的验收标准下，对某类试件进行检测时，能检出某一尺寸缺陷的概率[2-3]，也就是说，无损检测的可靠性问题可以转变成缺陷检出率的问题。即，缺陷检出概率用于衡量无损检测手段的可靠性[4-5]，其定量描述了无损检测检出特定类型、特定尺寸缺陷的有效性[6]。

2004年7月，美国空军研究实验室(AFRL)和联邦航空局(FAA)管理技术中心及NASA合作成立了模型辅助检出率计算研究(MAPOD)工作组[7]，该工作组利用数值模拟方法来计算实际工件中缺陷的POD曲线，目的是解决试验研究中试块加工难、成本高的问题。欧洲工程项目PICASSO[8]的目标是创立一个新颖独特的无损检测缺陷检出率曲线的仿真方法，该方法通过将仿真结果替换部分实验数据来得到POD曲线。

然而，实际的检测过程远比数值模拟中的条件更为复杂，影响因素更多[8-11]，因此用数值模拟代替实际的试验研究也是不现实的[12]。在可见的未来，工程中的POD曲线测量仍然需要采用试验测量的数据为基础，而数值模拟作为试验数据的补充[13-15]，可以代替一部分现场试验，或是完成POD曲线从某一检测条件下到另一检测条件下的移植[16-18]。

笔者针对粉末冶金涡轮盘(以下简称粉末盘)中夹杂缺陷的检出概率进行了以试验为基础的研究，设计并研制了专门的人工缺陷试样用于获得所需的检出概率数据，通过对数据的分析处理获得了特定检测工艺下的POD曲线。

1 试验准备

1.1 人工缺陷试样

人工缺陷试样为测试POD的关键，为了模拟粉末盘中的夹杂缺陷，在粉末盘材料内预制平底孔，通过考察超声检测技术对于不同尺寸平底孔的检出情况和信号幅度，获得POD曲线绘制所需的基础数据。

对于超声检测而言，缺陷的埋深会影响检出的概率。超声检测时，声波途经的声程为入射表面到目标深度的一次往返的路径。相同增益水平下，同样尺寸的缺陷，埋深大的声程更长，其回波幅度也会由于衰减的作用而更小。也就是说，为了使灵敏度保持一致，所需的增益随深度的增加而增大。所以一般情况，埋深更大的缺陷，更难以检测。

为了反映实际盘件中缺陷埋深的变化，采用从实际的粉末涡轮盘上取料的方式，制作了4组人工缺陷试块(见表1)，每组试块中含有相同埋深不同尺寸的缺陷，组与组之间的缺陷埋深不同。典型试样的外观如图1所示。

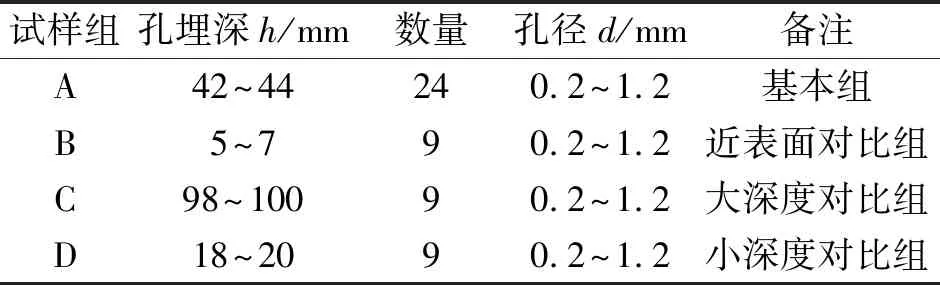
表1 用于POD测试的人工缺陷试样

图1 典型试样外观

1.2 仪器设备

文中所有的缺陷基础数据都采用水浸超声检测技术获取。所用的设备为以色列ScanMaster公司的LS-200盘件水浸超声检测系统。系统的超声发射接收部分为USC-100型号超声卡，其性能经检定部门检定合格，符合ASTM E317StandardPracticeforEvaluatingPerformanceCharacteristicsofUltrasonicPulse-EchoTestingInstrumentsandSystemswithouttheUseofElectronicMeasurementInstruments和GJB 1580《变形金属超声波检验方法》标准要求。

1.3 探头

目前粉末盘的超声检测采用水浸分区聚焦方法，对不同深度区域分别用不同焦距的聚焦探头覆盖。文章采用该技术对被检零件或试样实施检测，参照了中航工业集团标准Q/AVIC 06100-2015《航空发动机粉末高温合金盘锻件超声分区聚焦检测》确定每组试样所用探头的参数，如表2所示。

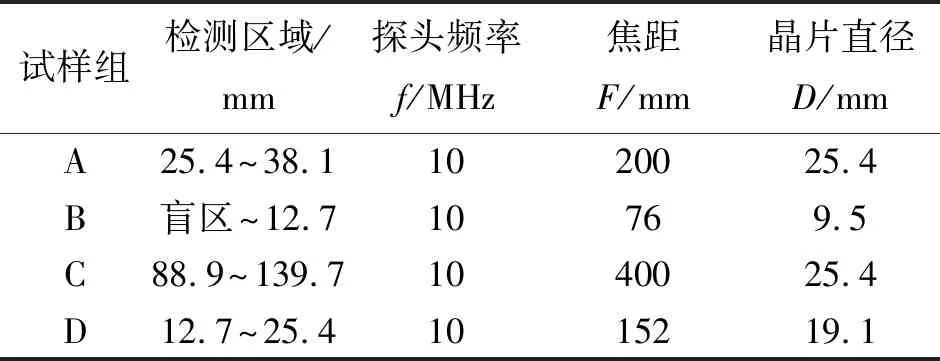
表2 试验所用探头的参数

由于探头的制作本身具有一定波动性，其性能也会存在波动性，因此即使采用相同型号的探头，也不能保证两个探头完全一致。探头个体之间的差异会导致检测结果存在分散性。为了使试验过程反映探头变化引起的检测结果波动，每组试验采用参数相同的两个探头分别进行检测。

1.4 对比试块

对比试块的作用在于：① 在粉末盘检测前作为基准，调整仪器的灵敏度；② 在缺陷评定过程中作为基准，对缺陷的尺寸进行定量。

文中的对比试块采用与盘件同材料、同工艺的粉末高温合金材料制成，试块中包含埋深为1.6～101 mm的平底孔人工缺陷，平底孔孔径为0.4 mm。

1.5 检测人员

检测人员负责检测过程的实施，所有的检测都要靠检测人员的操作来实现，因此检测人员对于检测结果具有重要影响。由于影响因素众多，检测人员的影响难以量化。故，试验中考虑到人员因素影响，由不同的检测人员重复所有的试验。

检测人员的简要信息如表3所示。

表3 参与试验的检测人员信息

1.6 试验设计

影响缺陷检出概率的因素众多，如检测工艺、缺陷埋深、缺陷取向、操作人员的熟练程度等。笔者选择了其中几个比较重要的因素来设计POD曲线的测试试验。为此引入了多组变量，包括：① 探头，采用2组探头分别进行试验;② 缺陷埋深，采用4组不同埋深的人工缺陷;③ 检测人员，分别由3名超声检测人员进行试验;④ 仪器校准，每名检测人员重复进行3次缺陷检测与评定，每次检测前进行仪器校准。

通过以上的方式，每个缺陷尺寸可以获得54个缺陷评定的数据点，用于后续POD曲线的建立。

2 缺陷检测概率曲线的试验测定

2.1 仪器校准(灵敏度调整)

仪器校准对于保持检测设备状态的稳定是至关重要的。对于POD曲线的测试，准确有效的仪器校准能保证检测结果的一致性，从而使得到的数据具有有效性。当仪器或探头发生了可能影响检测结果的变化(如更换探头、改变灵敏度)时，都需进行校准。

校准的实施采用对比试块。由于两点才能确定一条直线，因此正确的校准至少需要测量两个点。对于文中试验，由于灵敏度的调整过程是通过测定TCG曲线(深度补偿曲线)来完成的，故灵敏度调整完成即完成了校准。具体方式为：记录每个平底孔达到80%时的增益水平，建立TCG曲线。利用TCG曲线可以建立检测时的灵敏度，开启TCG功能后，深度范围内的φ0.4 mm当量尺寸的缺陷均达到80%水平。

2.2 人工缺陷的超声C扫描检测

采用超声C扫描成像进行试块中人工缺陷的检测。检测时扫描速度采用恒定线速度的方式，设置为仪器允许的最大值。检测速度的具体数值由检测系统根据脉冲重复频率和扫描间距自动调节。考虑缺陷在盘件中的平面位置，针对每组试块，分别将人工缺陷试块摆放在不同半径处，其中一次使试块摆放靠外侧，另一次摆放在靠中心的位置，以模拟缺陷在盘件中的不同位置。放置好试块后，进行缺陷的扫查。每次试验将埋深相同的试块一并扫查，闸门只需设置为覆盖试块中的缺陷埋深。

2.3 缺陷尺寸的评定

采用当量评定法来估计缺陷的尺寸，即：将缺陷的回波幅度与规则形状的人工反射体(一般为平底孔)的回波幅度进行比较，如果两者的埋深相同，反射波高相等，则称该人工反射体的反射面尺寸为缺陷的当量尺寸。

由于自然缺陷类型繁多，故不可能使人工反射体与所有的缺陷都对应。大部分情况下，缺陷的反射信号幅度与人工反射体的反射信号之间存在差异，此时需要进行相应的换算。根据声学理论，声波幅度与反射体面积成正比，即

(1)

式中：AF和A0分别为自然缺陷和人工反射体的反射信号幅度；d0为人工反射体(平底孔)的直径；dF为自然缺陷的当量尺寸。

由于影响缺陷反射回波幅度的因素很多，当量法确定的当量尺寸并不是缺陷的真实尺寸。为了简化计算，避免将当量尺寸直接作为缺陷实际尺寸使用，在记录和比较缺陷尺寸时并不直接采用换算出的当量尺寸，而是采用以分贝值表示的方法，其一般形式为

φd+Δ

(2)

Δ=20lg(AF/A0)

(3)

式中：d为当量评定时的平底孔直径；Δ为以分贝值表示的缺陷反射信号幅度与基准平底孔反射信号幅度的比值(可以为正或负)。

3 数据分析和曲线绘制

3.1 超声检测数据的处理

在理想情况下，尺寸大于临界验收尺寸的缺陷，其检出概率应为100%，尺寸小于等于临界验收尺寸的检出概率为0，此时不会出现漏检或误报的情况。

然而实际上，缺陷的检测尺寸并不一定等于缺陷的实际尺寸，例如一个尺寸为1 mm缺陷的评定结果可能是0.5 mm或1.5 mm。如果检测的次数足够多，可以看出缺陷的检测尺寸呈正态分布。记缺陷的实际尺寸为a，缺陷的检测尺寸为。对于每一个a值，对应的满足期望为μ(a)，标准差为σ(a)的正态分布

～N[μ(a),σ(a)]

(4)

式中：N为正态分布。

对于特定的临界尺寸aC，有可能大于aC，也可能小于aC。

POD(a)=P(|>aC)

(5)

当a取不同值时，可计算不同的POD值，得到特定检测技术下的POD曲线。

需要说明的是，在计算检出概率时，并不关心缺陷检测尺寸的绝对值，只需比较其数值与临界尺寸之间的关系，文章以缺陷的检测信号幅度作为缺陷检测尺寸的度量。也就是说，文中与缺陷检测尺寸相关的量(如和aC)均以百分比表示，对应于显示屏上反射信号的幅度。对于达到饱和(超过100%)的超声信号，通过记录信号80%时的增益水平并与基准值比较，换算得到其等效的信号幅度，换算后的缺陷信号幅度可能超过100%。由于缺陷的检测信号幅度与缺陷检测尺寸具有一一对应的关系，因此这一处理不会影响最终获得的POD数据。

3.2 线性回归模型选择

a与之间定量关系的确定是计算POD(a)的第一步。

根据线性回归理论，随机变量y和自变量x之间满足以下关系

y=xβ1+β0+ε

(6)

式中：β1为斜率;β0为截距;ε为残差，满足ε～N(0,σ2)的正态分布。

令y分别取和ln()，x分别取a和ln(a)，可以得到4组两两配对的数据组，绘制于坐标图中，并采用线性回归的方式进行拟合，得到如图2所示的拟合结果。

图2 4种数据拟合方式得到的线性拟合结果

从图2中可以清楚地看出，ln(a)和ln()之间具有最佳的线性关系。表4列出了4种拟合方式得到的拟合优度，也可以得到相同的结论。

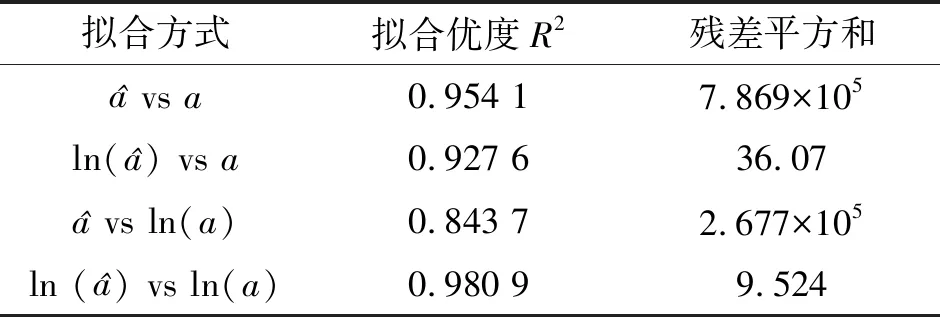
表4 4种拟合方式的拟合优度和残差平方和

ln()=β1ln(a)+β0+ε

(7)

回归得到的是β1和β0的估计值，同时,还可以得到残差方差σ2的估计值

(8)

得到的估计值和标准偏差如表5所示，这些值将用于后续POD函数中参数的计算。

表5 ln() vs ln(a)回归模型中各参数的估计值和标准偏差

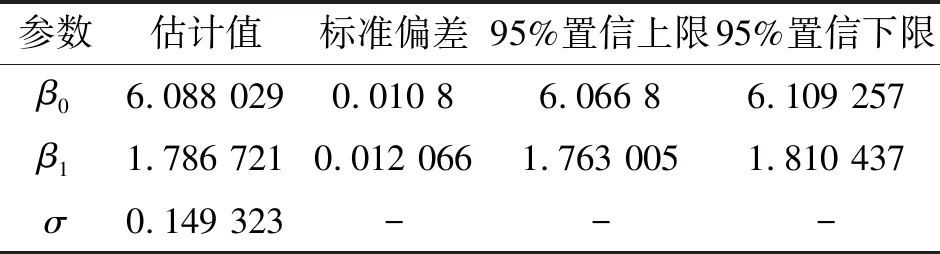
表5 ln() vs ln(a)回归模型中各参数的估计值和标准偏差

参数估计值标准偏差95%置信上限95%置信下限β06.088 0290.010 86.066 86.109 257β11.786 7210.012 0661.763 0051.810 437σ0.149 323---

3.3 POD曲线的绘制

ln()～N(μ,σ2)

(9)

式中：μ为其数学期望，与缺陷的判定(即验收的临界值)有关;σ表征分散性，可以通过3.2节中各参数的估计值和偏差计算得到。

根据POD的定义，POD是一个累积分布概率函数

POD(a)=Φ(t)

(10)

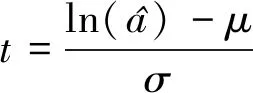
(11)

式中：Φ(t)表示标准正态分布的累积分布概率函数(CDF)，即正态分布N(0,1)中，所有小于等于t的值出现的概率之和。

将式(7)代入式(10)，可以得到以a为自变量表示的POD(a)函数

(12)

为了与前述的μ和σ区分，采用a作为下标，其与3.2节中各参数之间的关系为

(13)

σa=σ/β1

(14)

利用3.2节中得到的β0、β1和σ的估计值,可得到μa和σa的估计值。

利用β0、β1和σ的标准偏差，可以估计μa和σa的偏差[13]。

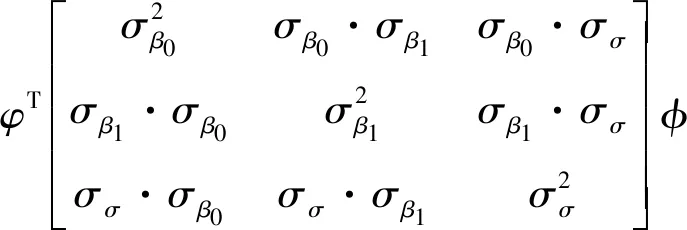
(15)

(16)

计算结果如表6所示。

表6 POD(a)函数中各参数的估计值和标准偏差

可以绘出POD关于缺陷尺寸a的检出概率曲线。根据新检测值的分布，可以得到POD的置信区间，一并绘于图中。

图3 粉末盘缺陷的POD曲线

3.4 POD曲线的解释

POD曲线描述了缺陷的检测概率与缺陷尺寸之间的关系。中心的实线即为检出概率曲线，上下两侧的虚线分别代表95%的置信线。其意义为：以原工艺执行一次新的检测，缺陷的检出概率有95%的概率落在两条虚线以内。

从图3中还可以得到几个重要的指标：

(1)a50代表以50%概率检出的缺陷尺寸，该值除了与检测工艺有关外，还受到验收(或判废)标准的影响。对于粉末盘检测，缺陷的评定以φ0.4 mm-15 dB为限，超过该临界值的信号判定为缺陷，反之则为可接受的信号。从数值上看ln(a50)=μa，从曲线中可以读出a50=0.146。

(2) 与a50类似，a90代表以90%概率检出的缺陷尺寸。从曲线中可以读出a90=0.163。

(3)a90/95表示在95%的置信水平下，以90%概率检出的缺陷尺寸。从曲线中可以读出a90/95=0.167。

4 结论

针对粉末涡轮盘的超声分区聚焦检测工艺，实际测试了POD曲线。采用人工缺陷试样完成了POD测试试验，获得了不同尺寸人工缺陷的超声检测数据。根据数据特点确定了ln()-ln(a)为最佳的线性回归数据组，得到缺陷尺寸和超声检测信号之间的定量关系。利用统计工具，计算出POD曲线所需的关键参数μa和σa，绘制出特定工艺下的POD曲线，从曲线中得到了a50,a90和a90/95这几个关键数据。对于粉末盘中的夹杂缺陷检测，采用文中所述的检测工艺，在95%的置信水平下，以90%概率检出的缺陷尺寸为0.167 mm。考虑到工程设计时一般要求超声检测能够检出φ0.4 mm-15 dB(约相当于0.169 mm)的缺陷，文中描述的粉末盘超声水浸分区聚焦检测工艺的可靠性满足发动机设计要求。

文章提供了一种试验测定POD的方法。对于采用超声检测技术进行检测的其他材料和零件，可以参照文章所述的方法，制作人工缺陷试块，试验测定人工缺陷的响应信号，对数据进行统计分析后绘制出POD曲线，以此获得的a90/95等数据可以直接应用于发动机概率失效分析的计算。

笔者提供的POD测试方法，可以用于对特定的超声检测技术进行检测能力和检测可靠性评价。对于不同检测技术的能力比较，也具有一定的参考意义。