基于进化规划算法的导波频散曲线计算

,,

(1. 92330部队, 青岛 266103;2.海军驻武汉438厂军代室, 武汉 4300613.海军工程大学 动力工程学院, 武汉 430033)

作为一种新兴的无损检测技术，基于磁致伸缩效应的导波无损检测方法可以实现非接触、大范围及长距离的快速检测，是近年来国内外无损检测界研究的热点技术之一[1-2]。该技术的理论基础是导波传播理论及导波特性，其中导波最重要的两个特性就是频散和多模态特性：频散特性即波的传播速度随着频率的变化而变化，多模态特性就是一定频率下可以存在多个模态的导波，而最直观反映导波这两种特征的就是频散曲线，其是研究分析导波特性和利用导波实施无损检测时选择激励频率的重要工具。由于不考虑导波能量的泄漏，相对而言，求自由管道频散方程的实数解比较简单，并且计算方程实数根的算法很多，如二分法、牛顿迭代法、弦线法等。相对于自由系统中导波频散方程的求解，泄漏系统中的方程求解要困难得多，而导波在泄漏系统中的衰减特性通常使用复频率或复波数来描述[3-6]。ARISTÉGUI等[7]讨论了复频率和复波数的差别，发现复波数能更准确地描述导波的衰减。笔者提出了一种基于进化规划的加载流体管道中频散方程复波数求解的方法，充分利用了进化规划智能搜索的特点，大大简化了粗略和精确搜索反复求解的过程。

1 加载流体管道中导波频散方程的建立

假设管道材料特性是均匀、各向同性的线弹性体，管道为轴对称且无限长。对于各向同性的弹性固体介质，若不考虑体力的影响，其一般的弹性动力学柱坐标下的运动方程(Navier-Stokes方程)为[8]

(λ+μ)(

(1)

式中：u为位移矢量;ρ为材料密度;λ和μ为Lamé常数。

时间谐振位移矢量u通过Helmholtz分解表示为可压缩标量势φ的梯度和零散度矢量φ的旋度，即

(2)

将式(2)代入Navier 运动方程得

(λ+μ)·(φ+×φ)+

μ2(φ+×φ)=

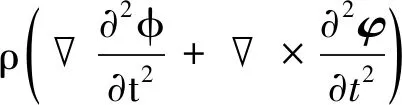
(3)

文章以管道中充满水为例进行分析，由于非黏性流体不支持剪应力，因而固-液和固-气交界处的边界条件不同于固-固交界面的边界条件。在管道内壁与流体的交界处，只有径向位移ur，正应力σrr及压缩应力σrz连续，而管道外表面上应力自由，则边界条件为

σrr=0,σrz=0，r=b

(4)

将管道中导波位移和应力表达式以及水中导波的位移和应力表达式代入边界条件，同真空中管道一样，产生一组特征方程，为以幅度A、B、C1、D1、E的矩阵形式

[Eij]·[H]=0

(5)

式中：H=[ABC1D1E]T;Eij为系数矩阵。

要使上述方程有非零解，其系数矩阵行列式必须为零，即

|Eij|=0，i,j=1,2,…,5

(6)

式(6)即为加载流体管道中的导波频散方程。

2 导波频散曲线计算

2.1 进化规划及变异算子

进化规划(Evolutionary Programming,EP)是三种典型进化算法(Evolutionary Algorithms,EA)之一，最早由美国FOGEL L J等[9]于20世纪60年代提出，后经FOGEL D B等[10]完善而成，其主要的应用介于数值分析和人工智能之间。同其他进化算法比较，EP主要有以下特点：① 对生物进化过程的模拟主要着眼于物种的进化过程，没有交叉算子，变异是唯一的操作方法；② 常用q选择运算，着重于群体中个体的竞争选择；③ 不必对变量进行编码，直接利用实数编码，以问题的可行解作为个体的表现形式，表述问题更加自然，搜索过程比较平稳，便于应用；④ 以n维实数空间上的优化问题为主要处理对象。

进化规划采用十进制编码，没有重组或交换算子，但有选择，进化主要依赖突变，操作控制简单。

在标准进化规划中，个体的表达形式为

i=xi+ζ·Fi(0,1)

(7)

式中：xi为父代个体；i为子代个体，由父代个体产生；ζ为一个变异尺度；Fi(0,1)为服从某一分布的随机数，也就是下面所讨论的变异算子。

式(7)表明，新个体是在旧个体的基础上添加一个随机数形成的，添加的随机数的数值与个体的适应度有关，适应度大的个体添加值也大，反之亦然。

根据表达方式，进化规划首先产生μ个初始个体，对其添加变异。然后从μ个旧个体及μ个新个体，共2μ个个体中根据适应度挑选出μ个个体组成新群体。如此反复迭代，直至得到满意结果。进化规划的工作流程类似于其他进化算法的流程，同样经历“产生初始群体-突变-计算个体适应度-选择-组成新群体”的过程，然后反复迭代，一代一代地进化，直至达到最优解。

通过进化算法的个体表现形式，即从式(7)可以看出，变异算子是该算法中主要的遗传算子，对算法本身的效率有着重要的影响。高斯算子的局部开发能力较好，柯西算子的全局探索能力较强，两类算子各有优点和不足，同时两者的变异性能具有一定的互补性。t分布的特性使得t算子能整合这两类算子的长处，从而更便利地找到最优解[11]。鉴于t算子的优良特性，文章将采用其作为进化规划算法的变异算子。

2.2 计算步骤

基于进化规划算法的频散方程求解的流程如图1所示，可具体描述为：

图1 利用进化规划算法计算频散曲线的流程图

(1) 参数初始化。输入管道内径ra、外径rb，材料密度ρ，弹性模量E,泊松比σ，流体密度ρf，流体中纵波速度cf；

(2) 建立频散方程。根据边界条件建立流体管道的频散方程|Eij|=0，设定初始计算频率f，频率步长fstep，计算频率最大值fmax；

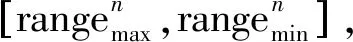
图2 频散方程行列式与实波数之间的变化关系

(4) 基于进化规划的频散方程求解。选择合适的t算子，在各个模态波数的定义域内求解计算频率下对应模态频散方程的复波数解k；

(5) 计算相速度cp。求出波数的虚部kimag为衰减系数catten，由实部kreal计算各个模态的相速度cp=2πf/kreal；

(6) 若f>fmax，转入步骤(7)，否则f=f+fstep，转入步骤(3)；

(7) 计算群速度cg。根据cg=dω/dk计算各模态的群速度。

2.3 t算子的选择

如上文所述，进化规划算法中主要通过变异控制整个进化过程，故变异算子的选择会直接影响算法性能的优劣。一般来说，当种群中目标函数值相差较小的个体可能位于最优点附近时，算法应该以局部开发为主；与目标函数值相差比较大的个体应加大变异尺度，在更广的空间范围内进行全局搜索，尽快逃离不利区域进入目标区域，算法的这种功能就只有通过合理控制进化变异算子来实现。t算子变异尺度由变异步长ζ和自由度n控制，文章将采用保持自由度n，变异步长ζ线性递减的t算子控制变异尺度优化进化过程。图3所示为使用不同变异步长算子时，基于tEP求解导波频散方程的进化过程。当变异步长ζ=0.1时，在经过很长一段时间才开始有向最优点进化的趋势，进化速率有点缓慢。ζ=2时，开始时间段内目标函数迅速下降，但经过二三十代后趋于平稳，此时收敛精度不高。采用变异步长ζ线性递减的t算子时，开始阶段ζ相对较大，可以看出目标函数值迅速收敛进入目标区域，ζ随着进化代数的增加也逐渐变小，算法开始以局部搜索为主来寻找全局最优值。变异步长ζ线性递减的t算子融合了大步长和小步长的优点，故采用这种变步长的t算子来求解频散方程。

图3 不同算子时基于t EP的频散方程求解进化过程

2.4 试验验证

使用自主开发的磁致伸缩导波检测系统(GWNDT-II)对某充水管道进行检测。管道的相关参数为：内半径，27 mm;壁厚,4 mm;密度,7 932 kg·m-3;泊松比σ,0.29;弹性模量E,210 GPa;管长6 m。水的属性参数为:密度,1 000 kg·m-3;纵波速度cf,1 500 m·s-1。

利用文章提出的算法计算得到该充水管道的导波频散曲线，如图4所示。然后，依据频散曲线选择不同的导波激励频率，得到不同激励频率时的导波检测信号如图5所示。

将由频散曲线得出的充水管道中不同激励频率导波的群速度理论值与试验检测值进行比较，如表1所示，可见各频率下试验值与理论值基本一致，误差很小。图6为两者的对比曲线，可更直观地表现出两者间的关系，从图中可看出试验值与计算曲线相吻合。由此证明了基于进化规划算法的频散方程求解方法的正确性。

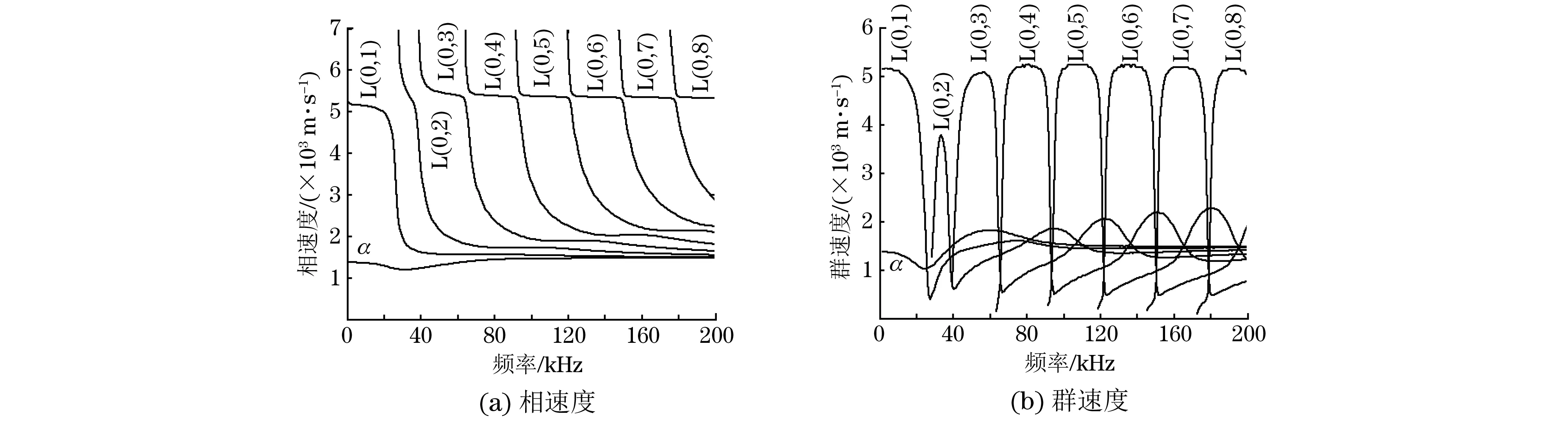
图4 充水管道的频散曲线

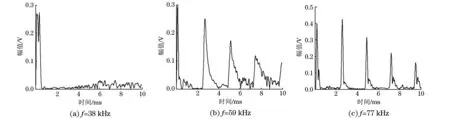
图5 不同激励频率时导波的检测信号

m·s-1

图6 群速度试验结果与理论计算值的比较

3 结论

提出了一种求解导波频散曲线的新方法，将进化规划算法应用到频散方程的求解中。相对于其他进化算法，进化规划算法的模拟主要着眼于物种的进化过程，没有交叉，突变是其唯一的控制方法，操作控制比较简单。频散曲线是反映导波在管道中的传播特征的最直观的手段之一，鉴于频散方程求解的复杂性和进化规划算法解决复杂问题的能力，将进化规划算法应用到流体管道的频散曲线求解中。通过比较，其计算结果和试验值拟合较好，且计算所得的频散曲线反应出的导波特性与试验反应出的导波特性是一致的。通过试验验证，充分证实该计算方法的可行性，且较其他方法便捷。文章以充水管道为研究对象，而同样的方法可推广到充满黏性液体管道、埋地管道等频散曲线的求解中，只是频散方程和边界条件不同，求解思路和过程是一致的。