多面函数在GPS高程拟合中的应用

韩子清，郭杨亮，马瑞娟，张顺幸

（1.西安科技大学测绘科技与技术学院， 陕西西安 710054； 2.河南省煤田地质局物探测量队，河南郑州 450009； 3.河南省地质矿产勘查开发局第五地质勘查院， 河南郑州 450001）

1 国内外研究现状

GPS技术可快速获取地面点三维坐标，在实际工作中应用广泛。GPS可获取一点处大地高，而我国采用的是正常高，二者的起算面不同。因此，将GPS获取的大地高转换为正常高是GPS高程应用的关键。正常高与大地高的转换如公式（1）所示。

式中：H正－该点处的正常高；

H大－该点处的大地高；

ζ－该点处的高程异常；

由公式（1）可知，一点处所测得的大地高减去该点处的高程异常，便可求得该点处的正常高。因此，GPS高程异常的确定是实现GPS大地高与正常高转换的核心。确定GPS高程异常主要有以下几种方法：联合平差法、数值逼近法、等值线图法、重力法等。出于对拟合精度与拟合方法的实用性、易操作性考虑，数值逼近法在实际工程中应用广泛。

数值逼近法通过数学表达式拟合出一个曲面，该方法在测区规律性变化明显的地区可获得较好拟合结果。主要方法有：多面函数拟合、多项式曲面拟合、克里格法、加权平均法、最小二乘配置、滤波与推估等。本文采用多面函数法进行拟合分析，采用实例进行求解高程异常。

2 高程拟合模型

2.1 多面函数拟合模型

多面函数拟合原理：根据测区内已有的重合点（同时具有GPS的大地高与正常高）进行高程拟合。函数逼近法，选用的拟合函数通常情况为多项式，而多面函数法，采用多元二次函数作为基底函数进行拟合。多面函数模型是Hardy教授提出，这种方法的基本思想是，任何不规则的连续曲面总可以用n个规则曲面的叠加来逼近［1］。

采用多面函数法进行高程拟合时，高程异常通过核函数的叠加来确定，如公式（2）所示。

式中：Q（x,y,xi,yj）为核函数

设有m个重合点，选取n≤m个点作为节点（xi,yj）（j=1,2…n），Q（x,y,xi,yj）表达式如公式（3）所示。

由公式（2）列立误差方程，如公式（4）所示。

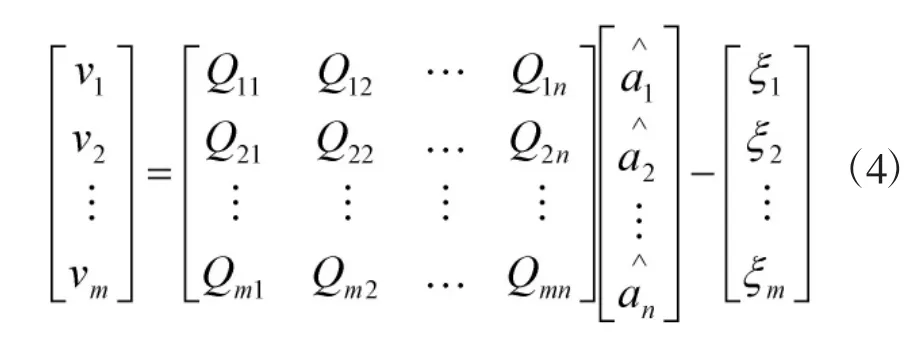
由公式（5）求解出未知系数，便可由公式（2）计算任意一点P（xk,yk）高程异常值，如公式（6）所示。

由多面函数的计算过程可知，首先要确定核函数。常用的核函数表达式有正、倒双曲面函数，锥面函数，三次曲面函数四种。

（1）正双曲面函数：

q为平滑因子，对核函数进行调节。

（2）倒双曲面函数：

q为平滑因子，对核函数进行调节。

（3）锥面函数：

c为待定参数。

（4）三次曲面函数：

C为待定参数。

多面函数进行高程拟合需要考虑以下三个方面的因素。

（1）核函数的选取。核函数应选取适合测区高程异常拟合的函数表达式。一般情况下从常用的函数表达式中选取，用不同的核函数表达式进行计算，选取拟合精度高的。

（2）平滑因子的确定。为让叠加得到曲面更符合测区的实际情况，需调节平滑因子的数值大小。平滑因子是通过多次试算来确定的，平滑因子在一定范围内计算结果稳定，其值过大或过小均会使精度降低。目前，对于平滑因子的确定尚无有效方法，需多次尝试［2-3］。

（3）核函数节点的选择。在测区重合点中选取若干个特征点（如测区的最高点、最低点和坡度变化较大的点）作为核函数节点，且节点要分布均匀，这样才能由规则曲面通过叠加所得的曲面更加符合测区的实际情况。

2.2 二次曲面模型

根据测区已有的已知点，采用一确定函数模型对测区的高程异常进行拟合。原理：根据已知点信息来构造一个数学曲面对该区域的高程异常进行拟合，利用拟合出的曲面信息来确定该区域内待定点的高程异常［4］。函数模型的表达式如公式（7）所示。

列立误差方程：V=Αβ-ξ，若已知数据的个数大于未知参数的个数，则可根据最小二乘原理［5］，解得出未知参数在

3 精度评定

（1）内符合精度

内符合精度σ内的计算如公式（8）所示。

vi-拟合的已知点的高程异常与计算后得到的高程异常的较差

n-为参与拟合计算的已知点个数

（2）外符合精度

外符合精度σ外的计算如公式（9）所示。

vi-检核点的已知高程异常与计算后得到的高程异常的较差

m-为检核点个数

4 算例分析

某地区布设E级GPS控制网，对其中23个GPS制点联测四等水准测，最低点高程138.66m（12号点），最高点高程307.97m（25号点）。重合点点位分布如图1所示。

计算中选取4，9，10，16，18，21，28，33，37共9个点作为检核点，其余14个点为参与拟合计算的点，拟合点均匀分布在测区内且包含测区内最高点与最低点。

本文在计算过程中分别选用锥面函数、三次曲面函数、正双曲面函数三种核函数进行计算，平滑因子反复试算，分别选用八个节点，十一个节点进行计算。计算结果如表1所示。

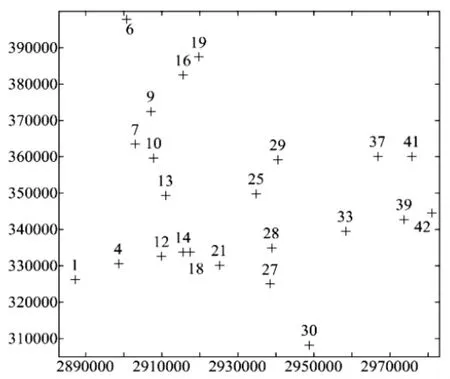
图1 计算区域GPS/水准重合点分布图

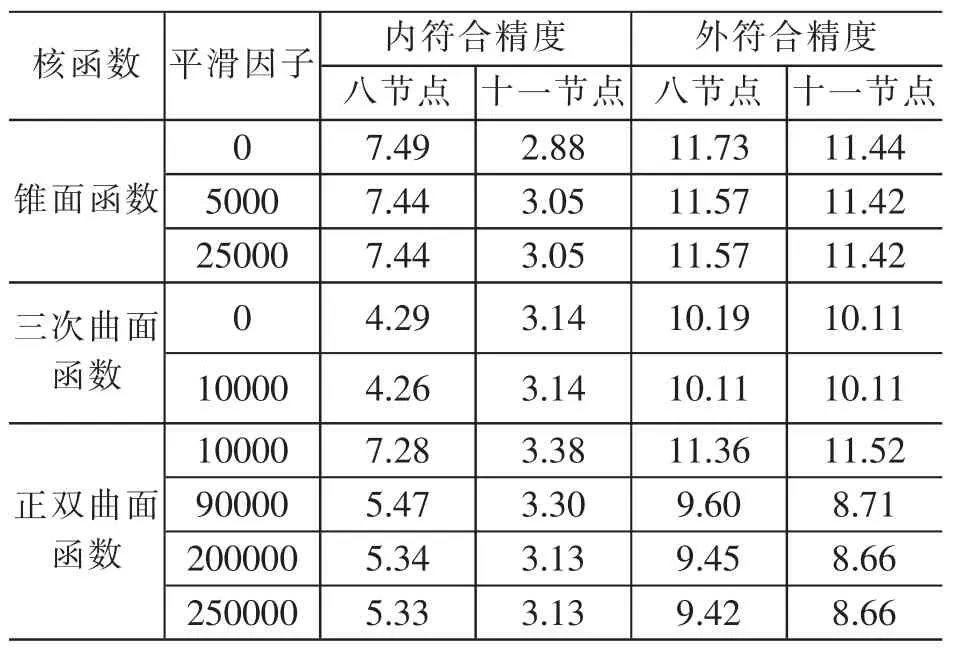
表1 多面函数拟合精度 /cm

绘制核函数节点为十一个点时的拟合残差如图2所示。

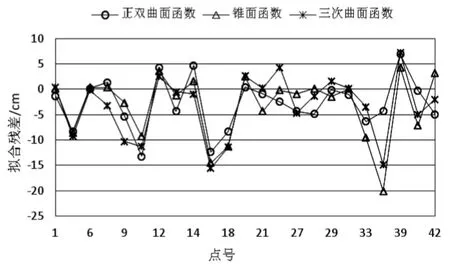
图2 十一节点多面函数拟合各点残差

采用二次曲面拟合时，内符合精度为6.72cm，外符合精度10.27cm。误差分布曲线如图3所示。

图3 二次曲面函数拟合各点残差

5 结论

通过对多面函数的分析可知：

（1）在拟合点相同的情况下，核函数的选取对拟合精度的影响较大，采用适合的核函数可明显提高拟合的精度。在本测区范围内选正双曲面函数为函数为核函数时，内外符合精度均高于锥面函数和三次曲面函数。

（2）不同核函数平滑因子值不同。当核函数选取锥面函数和三次曲面函数时，平滑因子的值对拟合精度影响很小，当选取正双曲面函数时，平滑因子对拟合精度影响较大，平滑因子通过反复试算来确定。

（3）采用十一个点为核函数节点时，拟合精度高于采用八个点时。说明核函数节点的选择要有代表性，适当增加节点数可更好进行曲面叠加提高拟合精度。

（4）由两种拟合方法比对结果可知，多面函数的内、外符合精度均要高于二次曲面的拟合精度。说明在该测区范围内，采用多面函数模型，选取合适的合函数与节点位置可取得好的拟合结果。