基于智慧课堂的高中数学概念课的教学设计
——以《向量减法运算及其几何意义》为例
2019-04-18安徽省合肥一六八中学邮编230601
安徽省合肥一六八中学 (邮编:230601)
托尔斯泰说过:“成功的教学需要的不是强制,而是激发学生的学习兴趣.”《数学课程标准》也明确指出:“高中的数学课程应该返璞归真,努力揭示数学概念、法则、结论的发展过程和本质.”因此,我们在教学中,尤其是进行高中数学概念课的教学时,一定要创设恰当的教学情境,激发学生的学习兴趣.现在的教学手段已经走向智能化,智慧课堂的使用让学生的学习变得有趣生动,所以我们作为一线教师更应该探索基于智慧课堂下的数学概念教学,让枯燥的概念课生动起来,让抽象的理论有趣起来,这样才能真正培养学生的数学核心素养.
本文以《向量减法运算及其几何意义》这节为例,在智慧课堂的辅助教学下设置的一堂全新的概念课.
1 创设情境,问题导入
先让学生观看视频——中央电视台《朝闻天下》中划龙舟大赛的报道,研究数学模型(图1):

图1

设计意图智慧课堂让枯燥的课堂生动起来,学生观看视频更能产生学习情感.
2 探索新知,深入研究
2.1 相反向量
思考实数的减法是说减去一个数相当于加上这个数的相反数,你能否用类比的思想定义向量的减法呢?
学生回答:减去一个向量相当于加上这个向量的相反向量.由此引入相反向量的定义.
定义1 与a长度相等,方向相反的向量,叫做a的相反向量,记作-a.
注(1)a与-a互为相反向量,即-(-a)=a;
(2)规定:零向量的相反向量仍是零向量.
讨论:你能否举出生活中长度相等且方向相反的量呢?
设计意图通过智慧课堂下的讨论互动,举出如作用力与反作用力,往返位移等,学生能由实实在在的物理量来体会相反向量的含义.
牛刀小试设O是正六边形ABCDEF的中心(如图2),

图2

设计意图通过具体的正六边形模型,概括出相反向量的性质:
(1)a+(-a)=(-a)+a=0;
(2)如果a、b互为相反向量,那么a=-b,
b=-a,a+b=0;

2.2 向量的减法
定义2a-b=a+(-b).
减去一个向量相当于加上这个向量的相反向量.求两个向量差的运算,叫做向量的减法.
小组探究(1)已知非零向量a、b,根据减法的定义,如何作图得到a-b?

设计意图(1)本环节强化了学生活动,利用智慧课堂实现生生互动,由定义及作图得到向量减法的过程,完全由学生完成,从而体现了学生的主体地位,在学生参与的过程中,教师要适时表扬,适时提出新的问题,激发学生兴趣;
(2)第(2)问是本节的重点,体现减法的形成过程;
(3)第(3)问培养学生严谨的科学习惯,同时也更加清楚地表示差向量.
总结归纳作图得到a-b的具体步骤:
(1)在平面中任取一点O;


口诀共起点,连终点,指向被减向量.
2.3 向量减法的几何意义
a-b可以表示为从向量b的终点指向向量a终点的向量.
3 巩固双基,挖掘内涵
例1如图3,ABCD中,
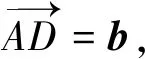
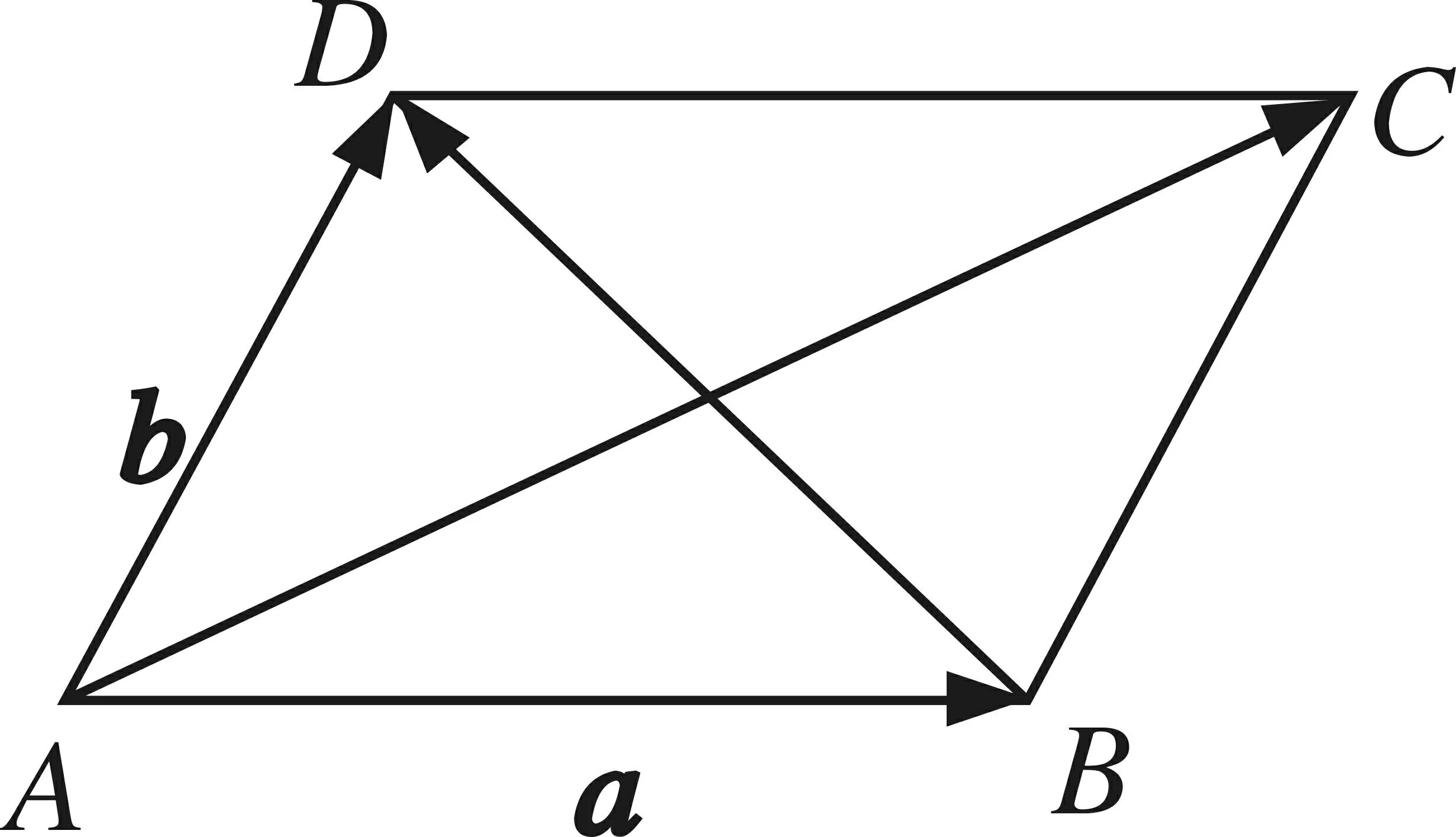
图3

归纳 (1)向量的加减法运算沟通了平行四边形的边与对角线;
(2)平行四边形是研究a、b、a+b、a-b的几何模型.
巩固练习如图4,已知a、b,求作a-b.

图4
设计意图考查学生对作图法则的理解,评讲时要特别注意第(3)(4)小题是共线的情形,减法法则仍然适用.另外,通过本例强调规范的作图方法及运算结果的体现.
在智慧课堂的辅助教学下,教师能全面监测到每位学生的练习结果,能很快了解到对于存在的问题,这样给出的教学评价能更全面、更有效.
变式提高



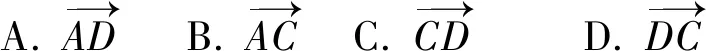


设计意图巩固向量加法首尾相连,减法共起点的法则,解决问题时还可以借助相反向量实现加减法之间的转化.从具体图形到数学符号,培养学生数学抽象和逻辑推理的数学核心素养.
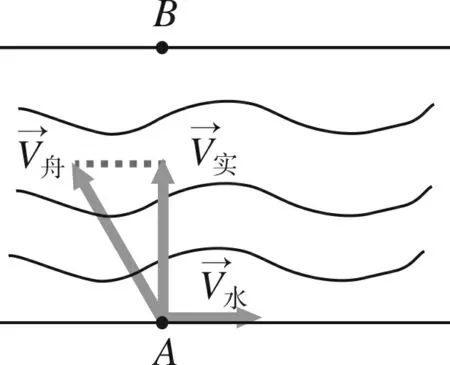
图5
通过智慧课堂的云端报告,选择题的答题情况更为清晰,教师能针对性地给出讲解,这样的教学也更有效.
4 问题解决,前后呼应
5 小结升华,布置作业

小结本环节由学生发言,教师归纳、总结、提升,指出类比和转化的思想是我们研究新概念与新事物的一般方法.
分层作业一、必做题:
1.课本:教材第91页习题2.2A组第4、6、8;
2.作业平台:校本作业.
二、选做题(思维拓展)
类比不等式||a|-|b||≤|a+b|≤|a|+|b|,试判断不等式||a|-|b||≤|a-b|≤|a|+|b|是否成立?若成立,给出相应解释.
6教学反思
当前的概念课常常采用“一个定义,几项注意”的方式,在概念的生成上着墨不够,但是概念课的教学必须让学生经历概念的形成过程,所以在教学设计之初,就要想着这节课怎样让学生参与进来.

这节课设置了五个与学生的互动,都是基于智慧课堂的辅助教学.第一个“讨论”环节,让学生在平板上讨论,每位同学都可以看到别的同学的想法,教学互动更加生动;第二个“牛刀小试”环节,不仅让学生巩固了相反向量的知识,还通过具体的正六边形模型,轻松概括出相反向量的性质;第三个“小组探究”环节,强化了学生活动,由定义及作图得到向量减法的过程,完全由学生完成,从而体现了学生的主体地位,学生学得主动,更充满了学习的兴趣;第四个“巩固练习”环节,除了考查学生对向量减法的几何意义的理解以外,还考查了学生的动手能力与变通能力,由于前面经历了概念的形成过程,学生轻松应对;第五个“变式提高”环节,从具体图形到数学符号,培养了学生数学抽象和逻辑推理的数学核心素养.
总之,随着教学手段的多样化,作为一线教师,我们一定要好好利用智慧课堂,探究智慧课堂在教学各个环节的有效性,去其糟粕,取其精华,让我们的一线课堂真正的有效和高效.
