基于Intel平台的Winograd快速卷积算法研究与优化

武 铮 安 虹 金 旭 迟孟贤 吕国锋 文 可 周 鑫

(中国科学技术大学 合肥 230022)

卷积神经网络(convolutional neural network, CNN)[1]由于感受野、权值共享和池化等特点，大大降低了神经网络训练需要的参数数目，使得更深层神经网络的使用成为可能，提高了训练的效率以及收敛的效果，成为了深度学习中最为典型且性能优越的一种网络模型.近年来，CNN更是在多个方向持续发力[2]，语音处理、文本提取、图像识别、通用物体识别、运动分析、自然语言理解甚至电脑波分析等方面均具有巨大突破[3-4].同时CNN也推动着人工智能的快速发展，ImageNet大赛[5]、Facebook图像自动标签、Google无人驾驶汽车以及第1个战胜世界围棋冠军的人工智能程序AlphaGo，这些无一不彰显着智能化时代到来的可能.对于CNN，其灵魂就是卷积[6]，而卷积不仅仅局限于CNN，在很多其他网络模型中也都有涉及.由此可见，卷积性能的好坏对于整个深度学习领域有着非凡的影响.对于卷积，当前主流的算法有GEMM[7]，FFT[8-9]，Winograd[10].这3种算法中除了GEMM，其他2种都是以增加一定的操作复杂度为代价获取更低的计算复杂度，从而提升卷积的性能，其中又以Winograd做卷积时计算复杂度最低[7].

尽管如今对于深度学习的探索和创新层出不穷，但是这些研究多数是基于NVIDIA GPU平台[11-14].本文另辟蹊径，选择Intel平台作为研究环境，其主要原因是Intel是高性能计算的支柱之一，但进军深度学习领域时间较短，因而具有更大的潜力和挖掘空间.以卷积举例，目前Intel平台仅对于GEMM算法有较高的支持力度.

本次研究选择Intel第2代Xeon Phi处理器KNL(knigths landing)7250作为研究平台，结合该平台特性对Winograd快速卷积进行实现与优化.一方面通过测试VGG19，对比Intel MKL(math kernel library) DNN(deep neural network)中卷积性能，最终取得了2倍多的加速比；另一方面通过测试常用卷积类型，对比Intel MKL DNN和NVIDIA cuDNN[7]，证明了本文的Winograd算法对于常用卷积类型具有很好的适应性且具有实际使用价值.本次研究，我们并不是要提供一个功能完善的卷积接口，而是借此让更多的研究者看到Intel平台在深度学习领域的潜力和价值，为Intel平台在深度学习领域的发展打开一道里程碑式的大门，也期望能够为深度学习领域的蓬勃发展带去更多的动力.

1 背景知识

1.1 卷积神经网络

20世纪60年代，Hubel和Wiesel在研究猫的大脑皮层中用于局部敏感和方向选择的神经元时发现其独特的网络结构可以有效地降低反馈神经网络的复杂度，继而提出了卷积神经网络.

CNN相比于其他的神经网络最大的优势在于局部权值共享的特征，使其在数据量较大的图像识别、语音处理等方面只需要非常少的网络参数，在保证收敛结果的同时大大降低了网络的运行时间，提高了网络的运行效率.

卷积是CNN的核心，而卷积的过程就是依据局部感受野的原理对输入通过卷积核进行特征提取，最终得到特征总结后的输出.

我们将输入记为INn,c,i nh,i nw(1≤n≤N,1≤c≤C,1≤inh≤Hin，1≤inw≤Win)，表示N个图片、C个通道以及图片大小为Hin×Win；卷积核记为FLTk,c,r,s(1≤k≤K,1≤r≤R,1≤s≤S)，表示K个特征映射、C个通道以及卷积核大小R×S；输出记为OUTn,k,o uth,o utw(1≤outh≤Hout，1≤outw≤Wout)，表示N个图片、K个特征映射以及图片大小Hout×Wout.由此，可将卷积公式记录为[15]

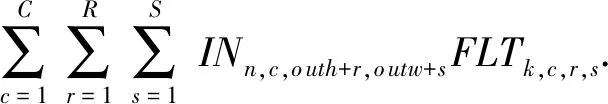
(1)

我们可将式(1)简写为

(2)

其中，*表示卷积操作.

1.2 Winograd算法

Winograd算法是基于1980年Winograd的最小滤波算法(minimal filtering algorithm)提出的一种快速卷积算法[16]，适用于小尺寸的卷积核做卷积，主要是通过降低卷积的计算复杂度从而提升卷积效率.

对于mininal filtering algorithm，以下简称为mini-filter算法.一维数据的情况下，当输出大小为m，过滤器大小为r，可将该算法记为F(m,r).此时，算法运算需要μF((m,r))=m+r-1次乘法操作[10].

一维的mini-filter算法可以表示成矩阵：

y=AT((Gw)⊙(BTx))，

(3)

其中，⊙表示hadamard乘积；x表示输入，w表示过滤器，y表示输出；AT，G，BT表示该算法的系数矩阵，其值由m和r决定，例如F(2,3)有:

从上述计算过程可以看出，其就是跨度为1的卷积操作.由此，我们可以把一维的mini-filter看成是一维的卷积操作.通过嵌套一维的mini-filter，可以得到特殊情况下的二维mini-filter矩阵：

y=AT((GwGT)⊙(BTxB))A，

(4)

可将此时的mini-filter算法表示成F(m×m,r×r).

将上述计算过程应用到CNN中的卷积，也就是算法1[10].

算法1. Winograd快速卷积算法(F(m×m,r×r)).

输入：

α2是输入块的尺寸，α=m+r-1；

相邻块之间的覆盖为r-1；

xc,b是索引为c的通道上索引为b的输入块；

XTile是转换后的输入重新布局得到的对应矩阵；

wk,c是索引为k的特征映射上索引为c的卷积核；

WTile是转换后的卷积核重新布局得到的对应矩阵；

BT，G，AT分别是输入、卷积核、输出的转换系数；

yk,b是k通道上索引为b的输出块；

YTile是转换后的输出重新布局得到的对应矩阵；

输出：yk,b,YTile.

fork=0 toKdo

forc=0 toCdo

wTile=Gwk,cGT；

scatter(wTile)→WTile;

end for

end for

forc=0 toCdo

forb=0 toTdo

xTile=BTxc,bB；

scatter(xTile)→XTile;

end for

end for

forζ=0 toαdo

forν=0 toαdo

end for

end for

fork=0 toKdo

forb=0 toTdo

gather(YTile)→yTile;*收集YTile中对应位置的数据，组成需要的输出块yTile*

yk,b=BTyTileB；

end for

end for

2 算法优化

对于二维数据，Winograd的卷积如式(4)所示，其中x表示输入块，w表示卷积核，y表示输出块，矩阵AT，G，BT则表示转换时的系数矩阵.由此，本次研究中Winograd设计原理如图1所示.

假设输入维度为[N,C,Hin,Win]，卷积核的维度为[K,C,r,r]，填充为0，跨度为1，使用Winograd算法F(m×m,r×r).为了方便描述，设t=m+r-1.

Fig. 1 The priciple of design for Winograd fast convolution图1 Winograd快速卷积设计原理

步骤1. 确定对应系数矩阵AT，G，BT，为了方便后续说明，我们假设wTile=GwGT，xTile=BTxB，所以Winograd算法变形为y=AT(wTile⊙xTile)A.

步骤3. 对每个卷积核做GwGT转换，并重排转换后的数据成1组矩阵.这组矩阵由t2个K×C的列优先的小矩阵组成，每个小矩阵索引为(tflt)(其中1≤tflt≤t2).

出于计算效率的考虑，通过对输入和卷积核转换后的数据进行布局重排，将核心计算⊙转换为矩阵乘，调用MKL中的矩阵乘接口.

出于内存重用的考虑，每层卷积层使用共有的内存空间存储输入、卷积核和输出转换后数据，这样不仅能够节省大量的内存空间，同时也有利于提高数据的空间局部性.

2.1 虚拟化填充

在深度学习中，卷积层进行卷积时，大小为1的零填充是十分常见的现象，因为这样不仅能够保留输入的边缘特征，同时也能够防止输出大小缩减太快以至于神经网络模型层数不深.

对于传统零填充，往往需要开辟出一块新的内存，再将原始数据和填充数据按对应位置赋值给这段内存.这种方式不仅访存代价高，而且会消耗大量内存.

为解决这一问题，本文提出了新的数据填充方式——虚拟化填充.我们定义2种数据类型：实数据和虚数据，其中实数据来自原始输入，虚数据为填充时边缘填充为0的数据.如图2所示，在模取输入数据时，假设输入数据已经填充完成，通过对数据位置的判断，决定该位置是虚数据置0，还是实数据对应原始输入数据值.

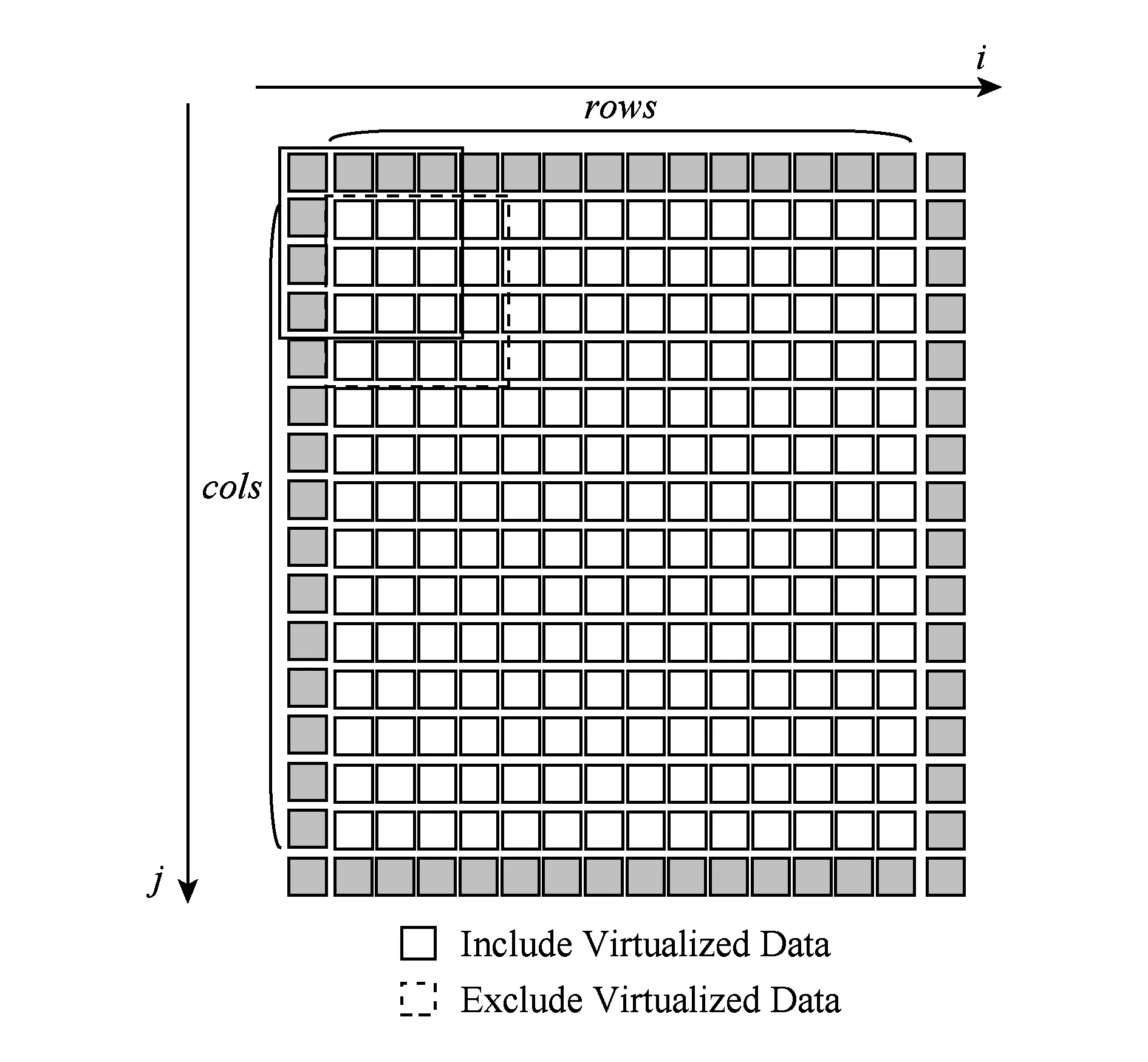
Fig. 2 Virtualized padding图2 虚拟化填充

2.2 分区填充

虚拟化填充解决了额外内存开销和填充后数据访存开销的问题，但是对于Winograd卷积中输入的转换部分，单纯的虚拟化填充需要在最内层循环中使用大量的分支判断语句来判定该位置是属于实数据还是虚数据，大大破坏了程序的连贯性.同时，分支预测失败会引起流水线空泡，降低程序的IPC(instructions per cycle)，影响程序的性能.

Fig. 3 Padding partition图3 分区填充

基于上述情况，提出了分区填充，旨在消除虚拟化填充中分支判断语句的存在，具体操作如图3所示.

将输入数据划分为3个区域——块中所有数据都是实数据组成的区域、块中整数行或列是虚数据的区域、块中整数行且列都是虚数据的区域.通过对输入数据进行分区，可以消除分支判断语句，从而避免分支预测失败对程序整体连贯性的影响，提高指令级并行度，保证程序的执行效率.

2.3 填充规模策略

虚拟化填充结合分区填充的方式针对大规模的数据填充起到了非常好的效果.但当数据规模较小时，由于内存空间的需求不是很高，访存时间比较少，可以尝试使用传统填充方法.虽然会造成一定的内存浪费和访存开销，但是会大大降低操作的复杂度，反而更为有利.

为了更进一步提升传统填充的效率，可以从减少频繁的内存空间分配和释放入手.如图4所示，在输入数据转换前分配一块内存空间，大小为nt(H+2ph)(W+2pw)，并将其通过线程索引进行分块绑定.对于某个线程，用于存储转换数据的内存空间大小为t(H+2ph)(W+2pw)，起始地址为initAddr+tIndex(H+2ph)(W+2pw) (其中，nt表示线程数，ph和pw表示横纵向的填充大小，initAddr表示起始地址，tIndex表示线程索引).

Fig. 4 The strategy for the scale of padding图4 填充规模策略

通过引入填充规模策略，针对不同规模的输入数据采用不同的填充方式：大规模数据采用虚拟化填充加分区填充，小规模数据采用优化后的传统填充，从而尽可能实现不同数据规模下的填充最优化.

2.4 合并策略

根据图1中Winograd快速卷积原理，在进行核心计算时，其本质是做t2×N个小矩阵乘，其中每个卷积核的小矩阵会同N个输入数的小矩阵相乘，因此可以考虑将这N个输入数据小矩阵合并到一起变成一个大矩阵再同卷积核的小矩阵做矩阵乘，从而增加矩阵乘的规模，提升矩阵运算的效率.

因为在做核心计算时的矩阵乘是并行执行的，一个线程负责数个矩阵乘.因此如图5所示，在做合并时，可以选择不同尺度的合并.以Merge值为合并尺度，从而将N个输入小矩阵合并为NMerge个CHout/mWout/mMerge的大矩阵，同对应的卷积核小矩阵做矩阵乘.一方面兼顾了并行时的多线程粒度，另一方面也兼顾了MKL矩阵乘接口的性能.

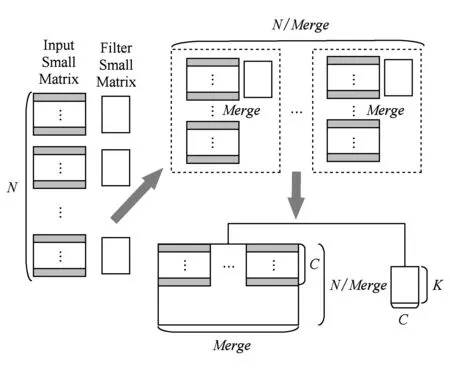
Fig. 5 Merge strategy图5 合并策略

2.5 不同尺度Winograd算法混合

Winograd快速卷积算法在某种意义上可以看成是传统卷积的扩展，不同点在于传统卷积在计算Output数据时是一次1个元素(对于二维数据，可以看成1×1的块)，而Winograd则是一次n个元素(其中n>1，同样对于二维数据，可以看成n×n的块).

通过F(2×2,3×3)同MKL卷积的比较中我们知道，两者对于不同规模的卷积各有优势.由此，不难猜想通过扩展Winograd算法的尺度，可以更好地适应不同规模的卷积(对于Winograd算法F(m×m,r×r)，m值的大小决定着算法的尺度).

本次研究中使用3种不同尺度的Winograd算法，分别为F(2×2,3×3)，F(3×3,3×3)，F(4×4,3×3).在混合使用时，可以分为结构级混合和数据级混合，前者是指当前卷积层选用3种Winograd算法中的一种做卷积，后者是指当前卷积层的卷积分成多个部分，每个部分分别使用3种Winograd算法中的一种.

2.6 分离转换替换统一转换

Winograd算法中，对于输入、卷积核和输出的转换可以表述为

xTile=BTxB，

wTile=GwGT，

y=ATyTileA，

其中,AT，G，BT为Winograd算法的转换系数，是由F(m×m,r×r)确定的已知数组.因此，在进行数据转换时，可以分为2种转换方式：分离转换和统一转换.

以输入数据为例说明，统一转换是将Winograd算法BTxB转换过程中的2次矩阵乘合并到一起，以输入模取的数据作为未知量x，由此获取转换后的数据xTile关于x的线性关系.

以输入数据为例说明，分离转换是将Winograd算法转换过程中的2次矩阵乘分开进行，以输入模取的数据为未知量x，由此获取第1次矩阵运算后得到的桥数据b关于x的线性关系；再以b为未知量，得到转换后的数据xTile关于b的线性关系.

对于统一转换，计算量少，但是所有的线性关系呈横向锯齿形，杂乱无规律，难以优化.对于分离转换，计算量较多，但所有的线性关系呈平面方形，平整有序，非常有利于向量化操作.

本次研究中，将前期的统一转换用分离转换替换，可以大大提升程序的性能.

2.7 混合统一批处理和分块批处理

随着batch的变大，处理的数据变得越来越多，使用到的内存也变得越来越大.当该层实际使用到的内存超出MCDRAM大小16 GB时，程序性能将会急速下降.

因此，对于大batch的卷积层，可以将batch分块处理，从而保证程序的性能.依据此，可以将batch的处理分为2种方式：统一批处理和分块批处理，前者是一次性处理所有batch，后者是将batch分块再处理.

分块的性能并不总是最优的，对于小batch，在进行Winograd卷积时，实际使用到的内存也会很小，此时如果仍然使用分块批处理，反而会因为无法发挥MCDRAM的优势以及多线程的效率，导致程序性能下降.因此，Winograd算法卷积实际使用到的内存在不超过MCDRAM大小时，选用统一批处理；实际使用到的内存超过MCDRAM大小时，选用分块批处理.

3 结果与分析

3.1 Intel KNL

Intel KNL是Intel第2代MIC架构Xeon Phi至强融合处理器[17]，是Intel首款专门针对高度并行工作负载而设计的可独立自启动的处理器，可继续做协处理器，也可独立做中央处理器.

如图6所示，Intel KNL处理器架构衍生于Intel Atom处理器，采用Silvermont架构的改进定制版和14 nm工艺，由38个Tile组成(最多有36个Tile处于活动状态)，核心数量可达72个，最大支持线程数为288，双精度浮点性能超3 TFLOPS，单精度浮点性能超6 TFLOPS.每个Tile包含2个Core，每个Core拥有2个向量化处理单元VPU，相同Tile里面的2个Core共享1块大小为1 MB的L2缓存.

Fig. 6 The structure of Intel KNL processor[18]图6 Intel KNL处理器架构[18]

Intel KNL相比于第1代Xeon Phi至强融合处理器，为了能够获取更高的性能，在架构方面有着非常显著的改变.Intel KNL的核布局不再是传统的环形布局，而变成了二维网格状布局，可以说是从线的布局方式提升到了面的布局方式，在进行核与核之间交互时具备了更高的效率；内存分成2部分：1)2个3通道的DDR4，每个通道可承担64 GB DIMMs，总容量可达384 GB；2)8个2 GB的MCDRAM设备，共16 GB.其中DDR4的访存带宽是90 GBps，MCDRAM带宽远超DDR4，可达450 GBps；MCDRAM既可做内存也可做缓存，据此，在启动设置时可以有3种模式：1)当MCDRAM做内存使用时，为Flat模式；2)当MCDRAM做缓存使用时，为Cache模式；3)当MCDRAM一部分做内存使用且一部分做缓存使用时，为Hybrid模式；单节点KNL可模拟成多节点，称之为SNC模式，分别是No SNC(All2All,Heimisphere,Quadrant)，SNC-2，SNC-4；支持AVX-512指令集，向量化操作更加完善.

本次研究中使用的是Intel KNL 7250，配置如表1所示：

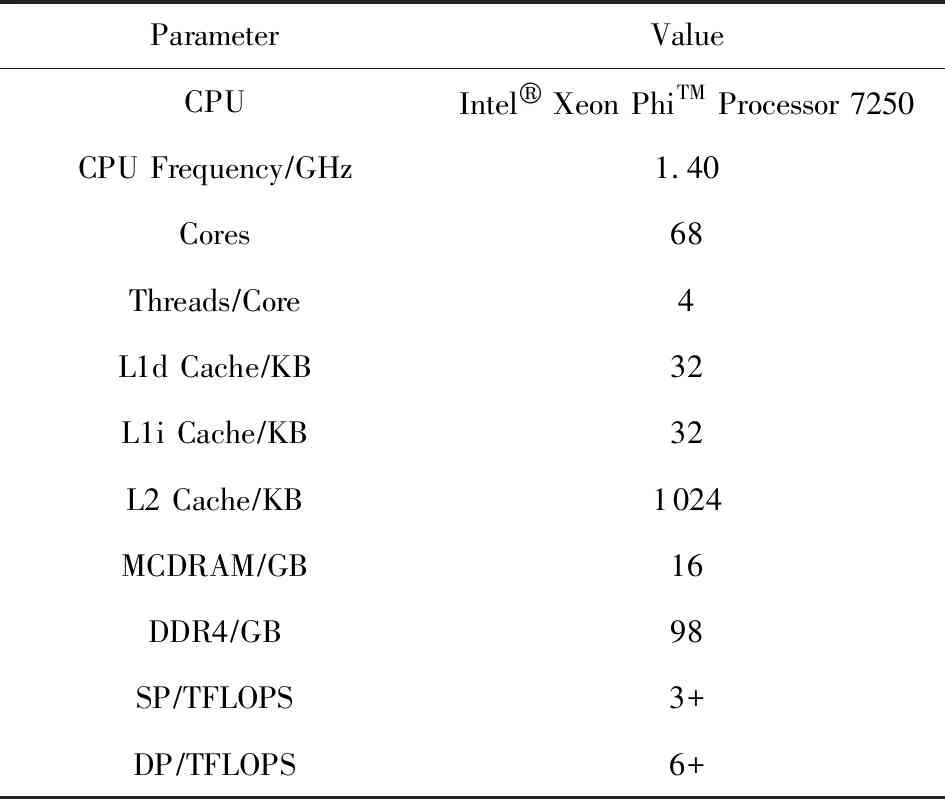
Table 1 Configure Parameters for Intel KNL 7250表1 Intel KNL 7250配置参数

3.2 性能测试

为了更好地验证本文Winograd的实现效果，故将实验过程分为3个阶段：

1) 选择VGG19作为测试网络，验证Winograd各级优化方案累加效果.

2) 同样选用VGG19作为测试网络，测试Intel KNL不同SNC模式和Memory模式对本文Winograd卷积性能的影响.

3) 抽取典型卷积网络模型AlexNet，GoogleNet，ResNet，VGG11，VGG16，VGG19中卷积层的卷积参数，测试本文的Winograd，Intel MKL DNN，NVIDIA cuDNN三者的卷积性能，对比验证本文Winograd对于常用卷积类型的适用性以及是否具有实际使用价值.

3.2.1 各级优化累加

通过测试VGG19中卷积在Winograd算法各级优化累加下的运行时间，对比Intel MKL DNN，如图7所示.其中，柱状图显示的是运行的总时间大小，折线图显示的是Winograd的加速比.

由图7可以看出：虚拟化填充在避免传统填充方式额外内存开销和访存弊端的同时引入大量分支判断，严重破坏了程序的连贯性，使得程序的整体性能很差，加速比仅有0.45；分区填充避免了填充虚拟化造成的大量分支判断，大大提升了程序的性能，使得加速比达到0.91；填充规模策略考虑小规模卷积使用优化后的传统填充方式，此时额外的内存开销和访存不会对程序性能造成太大的影响，通过该策略加速比达到0.92；合并策略通过配置最佳的合并尺度，充分发挥了矩阵乘的性能，加速比达到1.15；不同尺度Winograd算法对于不同规模的卷积具有更好的适应性，通过混合F(3×3,3×3)，加速比达到1.34.通过混合F(4×4,3×3)，加速比达到1.41；分离转换将数据转换分成2部分，使得转换过程具有工整对齐的计算公式，向量化得以充分发挥，加速比达到2.01；理论上，如果将Winograd快速卷积同Intel MKL DNN混合使用，最佳加速比可以达到2.11.

3.2.2 混合模式

Intel KNL新的架构特征，在很大程度上提升了访存的性能.同时，为了进一步提高核与内存、核与核之间的交互效率，加入了Memory模式和SNC模式[18].

Memory模式又分为Flat，Cache，Hybrid，取决于MCDRAM在处理器中的角色(memory还是cache).SNC模式又分为No SNC(All2All，Heimi-sphere, Quadrant)，SNC-2，SNC-4，取决于KNL处理器NUMA后的节点数.

通过混合2种模式，我们期望找出Winograd算法的最适情况.如表2所示：

Table 2 The Performance of Winograd with Different Modes表2 不同模式下Winograd性能 ms

SNC-2以及SNC-4模式下，程序性能均有很明显的下降，其他模式下性能略有差距.对于本文的Winograd算法，Intel KNL的最适SNC模式是Quadrant，对于Memory模式，Flat和Cache差距极小，考虑到误差的可能，可以认为两者皆为最佳模式.

3.2.3 常用卷积类型

为了进一步验证本文的Winograd算法对于常用卷积是否具有实际意义，我们抽取典型卷积网络模型AlexNet，GoogleNet，ResNet，VGG11，VGG16，VGG19中卷积层的卷积参数，测试对比本文Winograd，Intel MKL DNN，NVIDIA cuDNN的卷积性能.

在GPU的选择上，我们选取的是Intel KNL的同代GPU Tesla M40.因此在对比时要综合考虑硬件平台本身性能的差距，其中KNL7250的单精浮点性能是6.1 TFLOPS，Tesla M40的单精浮点性能是7 TFLOPS，所以时间计算为

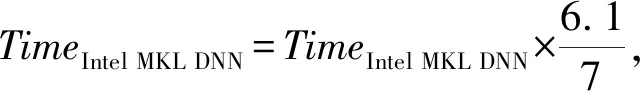
考虑不同卷积运行时间差距太大，可以将Intel MKL DNN的卷积时间作为标准，从而直接对比三者间的性能比

PerformanceIntel MKL DNN=
TimeIntel MKL DNN/TimeIntel MKL DNN，PerformanceNVIDIA cuDNN=
TimeIntel MKL DNN/TimeNVIDIA cuDNN，PerformanceWinograd=
TimeIntel MKL DNN/TimeWinograd.

我们总共抽取了46种不同规模的卷积，并按照计算量从小到大排列，分别就无填充和填充2种情况做测试，结果如图8和图9所示:

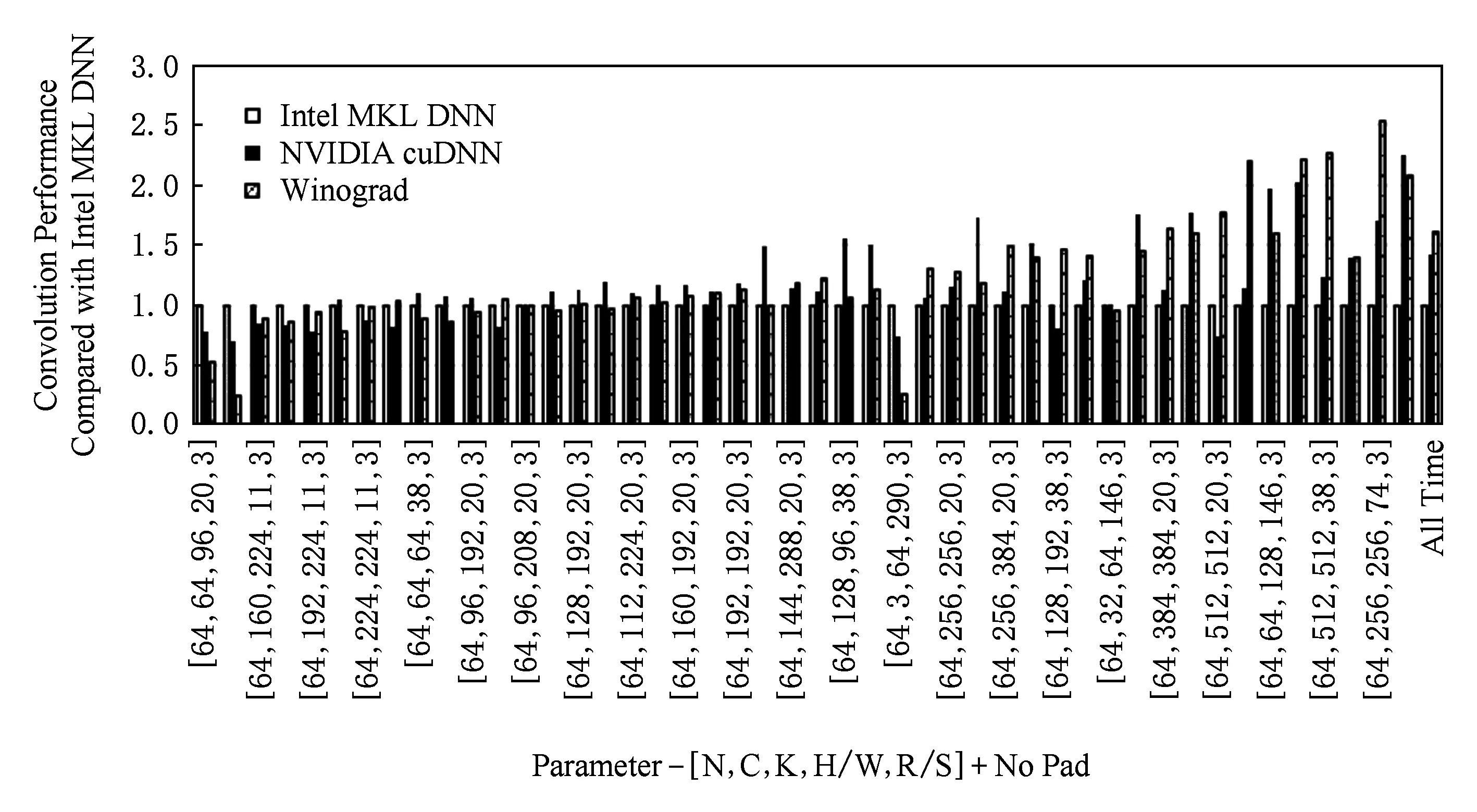
Fig. 8 Different convolution performance comparison with no pad图8 无填充下的不同卷积性能对比

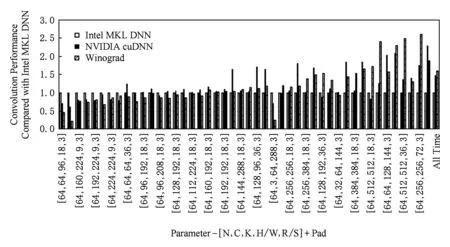
Fig. 9 Different convolution performance comparison with pad图9 填充下的不同卷积性能对比

从总体卷积来看，无填充和填充情况下，本文的Winograd算法相比Intel MKL DNN有61%和60%的性能提升，相比NVIDIA cuDNN也有13%和8%的性能提升.

从单个卷积来看，无填充和填充情况下，有性能提升的卷积占总数的67.4%和58.7%，性能相当的卷积占总数的17.4%和13%；卷积的规模越大，Winograd算法的性能往往越好.

综上可得，本文的Winograd快速卷积对于大多数常用卷积类型具有性能提升，且大规模卷积性能提升最为明显.在对比Intel MKL DNN时具有明显优势，即使对比NVIDIA cuDNN也是略胜一筹，可见本文的Winograd快速卷积具有实际使用价值.

4 总结展望

通过在Intel KNL平台上对Winograd快速卷积的研究与优化，一方面以VGG19作为测试网络，对比Intel MKL DNN，最终提升了1倍多(加速比2.01)的卷积性能；另一方面，测试常用卷积类型性能，对比Intel MKL DNN和NVIDIA cuDNN，证明了本文的Winograd算法对于常用卷积类型具有很好的适用性且具有实际使用价值.但这并不是结束，相反这仅仅是一个开始，未来仍有许多的路要走，比如：提升算法对于小规模卷积的适用性；合并策略在进行尺度判断时，仍需要手动配置，无法自动决定最佳的合并尺度； 统一批处理和分块批处理的判断仍然需要进行大量测试以决定最终的边界，简单地以MCDRAM的大小作为边界并不是最合适的方案；Intel MKL DNN和Winograd最适情况的标准仍需研究界定等.同时，基于算法的角度考虑，不同尺度的Winograd算法对于不同规模的卷积适应性更强，可以从这一方面出发，通过进一步扩大Winograd算法的尺度提升性能；基于Intel平台的考虑，可以从数据预取出发，进一步提升算法性能.未来我们将从这些方面入手，对Winograd算法做进一步的完善.

本文研究工作并不是去优化一个完善的快速卷积算法，更多的是彰显Intel平台在深度学习领域的潜力和价值，为其后续发展提供重要的指导意义，借此为人工智能领域的蓬勃发展贡献一份力量.