一种基于斯格明子介质的高效存内计算框架

刘必成 顾海峰 陈铭松 谷守珍 陈闻杰

(上海市高可信计算重点实验室(华东师范大学) 上海 200062)

当今世界已进入大数据时代，各种现代应用对数据处理速度的要求越来越高.然而在传统的冯·诺依曼架构中，数据的存储和处理各自分离，同时数据量与处理速度之间的差距也在逐步拉大，严重制约了系统效率的进一步提高.为了克服这个困难，文献[1-2]提出了新型存内计算(processing in memory, PIM)架构，并受到广泛关注和研究[3-4].在存内计算架构中，存储单元和计算单元在内存中紧密地结合在一起，使得数据可以直接在内存中就地进行处理，从而极大地减少了数据在内存和处理器之间的频繁移动且增加了数据处理的并行性.

虽然存内计算架构在一定程度上缓解了“数据搬运”的瓶颈问题，然而由于传统存内计算建立在易失性存储器介质之上，其物理特性限制导致整个系统泄漏功耗和动态功耗随着处理数据量的增加而急剧增长.近期各种新型非易失性内存介质(non-volatile memory, NVM)正因其区别与传统介质的低漏电率、高密度等一系列优良的特性而受到广泛关注[5-7].典型的包括相变存储器(phase change memory, PCRAM)、自旋力矩存储器(spin-transfer torque memory, STT-RAM)、赛道型存储器(racetrack memory, RM)等.其中RM通过将多个比特的数据存储在一条类似磁带的纳米线上，提供了比自旋力矩存储器更高的存储密度，比相变存储器更高的写入寿命，以及接近静态随机存取存储器(static random access memory, SRAM)的读写速度[8-10].

赛道型存储的本身物理结构决定了其不但适用于存储数据，也非常容易组成各种逻辑结构来进行数据处理，因此可以用来作为存内计算的介质.第1代赛道型存储器是基于磁畴壁(domain-wall)介质的，文献[11]在此基础上提出了一种较为通用的存内计算架构.然而这种基于磁畴壁介质的存内架构依然需要大量的CMOS(complementary metal oxide semiconductor)外围电路来进行辅助计算，导致了计算单元体积和能耗的增加.

最近新型的基于斯格明子介质的第2代赛道型存储器被提出[12-15].相比磁畴壁介质，斯格明子介质具有密度更高、能耗更低、稳定性更强以及更少受限于材料等一系列优良特性，非常适合作为下一代存内计算的介质.同样这种介质特性也非常适合使用在嵌入式系统中，甚至可以用来构建基于嵌入式系统的移动存内计算框架.然而目前对于斯格明子介质的研究主要集中于硬件存储功能，缺乏关于计算功能的研究，系统层次以及具体应用实现也很少涉及[16].另一方面由于斯格明子-赛道型存储器特有的条带状物理结构，使其具有特有的顺序读写特性，如何用其替代现有存内计算架构下的存储单元也是亟待解决的问题.

针对以上问题，本文提出了一种基于斯格明子介质的存内计算框架，主要贡献有4点：1)结合斯格明子介质本身的物理特性，由斯格明子逻辑门组成加法器、乘法器等计算单元并进行优化，极大地减少了CMOS辅助电路的使用，提高了计算效率；2)在硬件电路层面上对于基本存储单元读写端口数等参数进行探讨，并通过实验优化配置；3)在系统层上对内存的地址映射方式进行改进，提高了整个系统的运行效率；4)以通用的图像锐化程序为例详细说明了程序在内存框架中的工作流程，同时将本文提出的基于斯格明子介质的内存框架与目前最先进的基于磁畴壁的存内计算框架进行实验对比.

1 基于斯格明子介质的存内计算框架

基于斯格明子介质的存内计算主要包含2部分：基于斯格明子介质的存储单元和计算单元，其中存储单元即斯格明子-赛道型存储器，是整个框架的基础.

1.1 斯格明子赛道型存储器件

斯格明子-赛道型存储器[12-13]，区别于磁畴壁-赛道型存储器，是一种基于斯格明子编码的非易失性存储器.如图1所示，数据通过斯格明子编码之后存储在一条单一的铁磁纳米线(nanowire)器件上.纳米线上的斯格明子由电压控制的磁各向异性(voltage-controlled magnetic anisotropy, VCMA)门所隔离，每2个门之间存储一位数据.如果此区间内存在斯格明子则代表数据1，如果不存在斯格明子则代表数据0.斯格明子-赛道型存储器件有3项基本操作：移位、读和写，其中具有移位操作是其最重要的特性.

Fig. 1 Skyrmion based nanowire device图1 斯格明子-赛道型存储器件结构图

斯格明子-赛道型存储器件的移位操作，是指在磁各向异性门打开时纳米线上的斯格明子可以通过在存储器两端移位端口(shift port)施加电流来进行向左或向右移动.为了保证移位操作之后记录在纳米线上的数据不丢失，在纳米线两端应当有冗余的存储位供位移操作使用.整体来说所有比特数据的移位都类似于磁带操作，和移位寄存器类似.

斯格明子-赛道型存储器件读、写操作的基本原理类似.在存储器器件中有读写端口(write/read port)，即沿着纳米线方向放置的一个强磁化铁磁层，但是其和纳米线之间由较薄的绝缘层隔开.这样的三明治结构形成了磁隧道结(magnetic tunnel junctions, MTJs).通过向写端口的MTJ结构中注入自旋极化电流(spin-transfer current)就可以在纳米线上产生一个斯格明子.同样读端口也是一个MTJ结构，通过检测读端口MTJ隧穿电导(tunneling conductance)的变化就可以得知纳米线上当前位置是否存在斯格明子，即数据是0还是1.需要注意的是，由于写和读操作只能在固定的MTJ端口处进行，因此纳米线上比特位数据的操作需要移动到与MTJ固定层对齐的位置才能进行，而移位操作的方向和速度取决于控制电流的方向和幅度.

1.2 基于斯格明子介质的存内计算框架

传统上所有的数据都是保存在和处理器分离的主存中，二者通过总线相连接.因此在程序执行过程中所有的数据都需要迁移到处理器中，并在处理完成之后再次写回.对于以数据为导向的应用，这将产生严重的通信堵塞，从而大大降低总体性能.此外在传统的内存中保存大量的数据也将产生明显的待机能耗.

为了克服上述2个问题，我们使用基于非易失性内存的计算架构.首先存内计算架构在一定程度上解决了数据传输瓶颈的问题，也减少了数据传输的能耗；其次非易失性内存在极大地减少待机功耗的同时也降低了内存的动态功耗.基于斯格明子-赛道型存储器的存内计算平台整体结构如图2所示，其中存内计算单元与存储单元以分布式的方式组合成存储-计算单元组，这样许多频繁处理数据的操作可以在内存内部完成而无需与外部处理器进行通信，从而极大地节省了时间与能耗的开销.同时分布式的内存处理单元也可以提供巨大的线程级并行性，从而极大地提高系统吞吐量.

Fig. 2 The structure of PIM platform图2 存内计算架构

在本文提出的基于斯格明子的存内计算框架中，内存存储单元由基于斯格明子的赛道型存储器构成，从而受益于其低漏电功耗、非易失性以及稳健性等优点.同时存内计算单元纯粹由基于斯格明子逻辑门的加法器、乘法器等组成，只需要极少的CMOS电路辅助，因此总体漏电功耗和处理数据所需的动态功耗和时间消耗都极大地减少.在本文提出的存内计算框架中，存储-计算单元组之间通过H型内部数据通路相连接，这样单元组与单元组之间的数据可以随时根据需要进行传输，而外部处理器(即CPU)主要负责将控制指令传输给内存内部的控制单元，由内部控制单元负责内存中存储与计算单元具体数据的调度处理.由于斯格明子既具有计算功能又具有存储功能，因此在本文提出的存内计算框架中，计算单元得到的结果将直接写入存储单元中，即存储单元本身完成了类似寄存器的时序逻辑功能.

2 基于斯格明子介质的计算单元设计

本节首先从硬件层面考虑，提出基于斯格明子逻辑门的加法逻辑单元和进位逻辑单元设计，再进一步提出整个全加器的设计，最后在全加器设计的基础上提出了基于斯格明子逻辑门乘法器的设计，并进一步对加法器进行了优化.

2.1 基于斯格明子逻辑门的加法逻辑

典型的逻辑和运算由2个异或门组成，然而异或逻辑门无法直接使用斯格明子器件实现.这个问题可以通过斯格明子逻辑门组合来实现[14-15].其中文献[14]实现了基于斯格明子的逻辑与门和逻辑或门，同时包含基于斯格明子的复制(duplication)逻辑，而文献[15]中实现了基于斯格明子的逻辑与非门和逻辑或非门.在此基础上本文构建了基于斯格明子的异或逻辑门.如图3(b)所示，基于斯格明子的异或逻辑门由1个或门，1个与非门以及1个与门组成.需要注意的是，图3(b)中OR2-Gate是与非门NAND-Gate的一部分，输入部分An和Bn分别代表数据A和B的第n位.正如图3(a)所示，A和B是一个存储在斯格明子纳米线上8 b的数据.在斯格明子纳米线上，如果某个位置存在有斯格明子，它就代表数值1；如果没有斯格明子，它就表示数值0.因此图3(a)以二进制形式表示A=10111001，B=10101110.

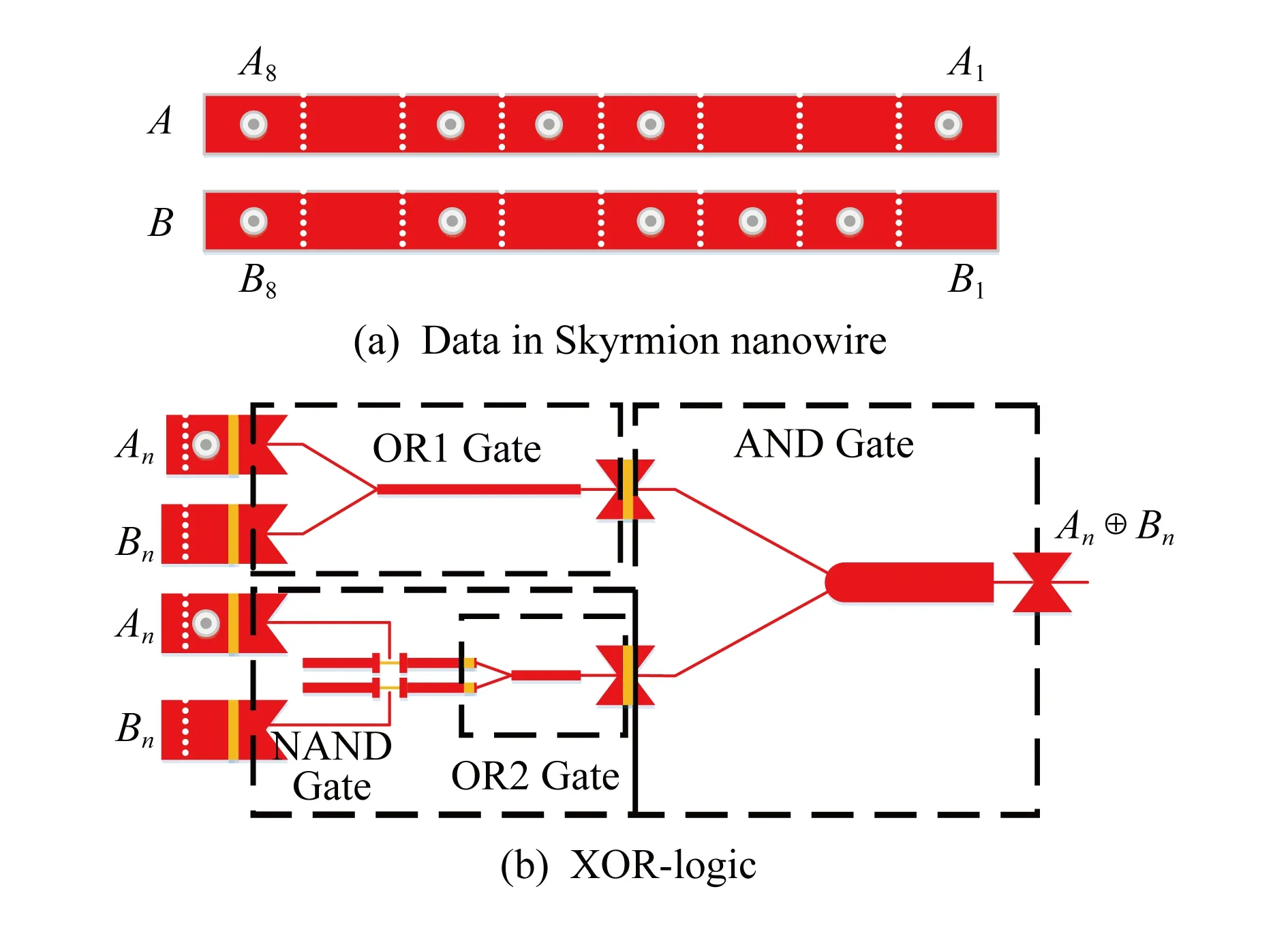
Fig. 3 Skyrmion nanowire-based XOR-logic图3 基于斯格明子的异或逻辑单元

当n=1时异或逻辑单元工作步骤有3个：

1) 操作数A1和B1同时进入逻辑门OR1和NAND.由于A1=1，B1=0也即有一个斯格明子进入逻辑门OR1，一个斯格明子进入逻辑门NAND.

2) 代表A1的斯格明子分别通过逻辑门OR1和NAND并保持不变.

3) 从逻辑门OR1和NAND出来的2个斯格明子同时进入逻辑门AND，最终合并成一个斯格明子,从而可以得到A1⊕B1=1.

通过基于斯格明子纳米线器件的异或逻辑单元我们可以实现带进位的加法逻辑单元(SUM=An⊕Bn⊕Cin，其中Cin为进位).即通过组合2个异或逻辑单元：第1个异或逻辑单元输入是An和Bn，输出是An⊕Bn；第2异或逻辑单元输入是An⊕Bn和Cin，而输出是当前位的进位和SUM.

2.2 基于斯格明子逻辑门的进位逻辑

一个典型的进位逻辑由3个与门和2个或门组成.图4显示了基于斯格明子逻辑门的进位逻辑单元具体设计细节.

Fig. 4 Skyrmion nanowire-based carry-logic图4 基于斯格明子的进位逻辑门

如图4所示，进位逻辑单元有3组输入：An和Bn，An和Cin，Bn和Cin，以及一个输出：Cout.其中输入Cin为第n-1位的进位，输出Cout为第n位的进位.进位逻辑单元具体实现细节有4点：

1) 代表上述3组输入第n位数值的斯格明子粒子分别进入了3个与门，即AND1～AND3.

2) 第1个与门AND1的输出和第2个与门AND2的输出将同时进入第1个或门OR1.第3个与门AND3的输出将在进入第2个或门OR2之前等待OR1的输出.

3) 第1个或门OR1的输出与第3个与门AND3的输出同时进入第2个或门OR1.

4) 第2个或门的输出即进位的值Cout.

2.3 基于斯格明子逻辑门的全加器

Fig. 5 Skyrmion nanowire-based full adder图5 基于斯格明子逻辑门的全加器

基于斯格明子逻辑门的全加器如图5所示，此全加器由3个主要部分构成：第1部分(PART1)是和运算部分，由第1个异或逻辑组成，它的输入是An和Bn，输出是An⊕Bn.同时第1部分还有一个复制逻辑(duplication)以便为第3部分(PART3)提供输入.第2部分(PART2)是进位逻辑，其输入是An-1，Bn-1，Cn-1，而输出是Cn即n-1位的进位.同时Cn会复制4份，其中2份作为第3部分(PART3)的输入，另外2份作为下一位加法的输入.第3部分(PART3)由第2个异或逻辑构成，其输入是An⊕Bn和Cn，即第1部分和第2部分的输出，而输出就是全加器的最终结果：SUM=An⊕Bn⊕Cn.

图5中的针孔形状部分代表一种能量势垒(energy barrier)[15]，这种能量势垒在电压为正的时候可以阻止斯格明子通过，而在电压为0的时候允许斯格明子通过，从而起到类似开关的作用.通过能量势垒的开关可以使得斯格明子同步进入逻辑门的2个输入端以保证逻辑门的正常工作.注意，当n=1时，An代表数据A的第1位，此时An-1不存在即无任何输入，Bn-1与Cn也相同.

不同斯格明子逻辑门的传播时延已在文献[14-15]中给出.基于已知的各种逻辑门的工作时间，当整个系统的工作频率为1 000 MHz时，通过计算得知全加器进行1位的加法需要11个时钟周期.考虑到能量势垒开关在使逻辑门输入同步的同时也使得各个逻辑门之间相互隔离，因此当进行多个位的加法时可以利用此特性对全加器的工作流程进一步优化.受CPU流水线优化技术启发，我们对全加器进行了优化：在1位加法计算完成之前就允许下一位的数据进入全加器，从而极大地提高了整体工作效率.

经过优化后的全加器电路时序图如图6所示.其中横坐标的数字1～19分别代表19个时钟周期，每个时钟周期为1 ns；纵坐标的Gate 1～13分别对应图6所示全加器中对应的13个逻辑门的控制电压，即每个逻辑门输入端口处能量势垒开关的电压.经过优化后的全加器主要时序逻辑为

Fig. 6 Timing diagram of 8-bit full adder图6 全加器电压控制时序图

1) 第1个时钟周期.Gate1～2，Gate5～7对应的控制电压为低电压，因此对应输入 端口的斯格明子(也即An，Bn，An-1，Bn-1，Cn-1)可以进入OR-Gate1，NAND-Gate2和AND-Gate5.为了保证输入同步，Gate3～4，Gate8～9和Gate11对应的控制电压为高电压.其他逻辑门对应的控制电压均保持低电压，因为这些逻辑门还未被使用.

2) 第2个时钟周期.Gate1～2，Gate5～7对应的控制电压变为高电压以阻止斯格明子进入对应逻辑门，同时Gate3～4，Gate9和Gate11的控制电压继续保持高电压以完成逻辑门同步功能.Gate8的控制电压从高电压转为低电压从而使得斯格明子进入OR-Gate8，其他逻辑门的对应控制电压依然保持不变.

3) 第3个时钟周期.Gate9的控制电压转为低电压以便斯格明子进入OR-Gate9，同时后续Gate10的控制电压转变为高电压以完成同步功能，其他逻辑门的控制电压保持不变.

4) 第6个时钟周期.Gate4的控制电压从高电压变为低电压以便斯格明子进入AND-Gate4；同时 Gate2的控制电压变为低电压以便允许下个比特的数据进入NAND-Gate2，后续Gate3依然保持高电压.

5) 第8个时钟周期.Gate10～11的控制电压转为低电压从而An⊕Bn和Cn对应的斯格明子可以进入 OR-Gate10和NAND-Gate11.Gate12～13的控制电压为了保持同步应变为高电压状态.同时Gate5～7的控住电压转为高电压，而Gate8的控制电压转为低电压.

6) 第13个时钟周期.Gate5～7的控制电压转为高电压以阻止斯格明子进入逻辑门，同时Gate8，Gate10，Gate11，Gate13的控制电压转为低电压.

7) 第14个时钟周期.可以通过输出端口是否有斯格明子判断SUM的值是0还是1，从而得到求和运算的第1个位数值.

8) 第15个时钟周期及以后.不断重复第10～14个时钟周期的状态，每隔5个时钟周期就可以读出和的下一位数值.

如图6所示，经过计算可以得知第1位的加法需要14个时钟周期(每个时钟周期1 ns)，而从第2位开始每5个时钟周期全加器就可以完成一个位的加法.这是由于经过优化后全加器内部各个逻辑门之间相互独立运行，从而可以获得类似流水线的优化效果，考虑到在进行大量数据处理时或者随着运行频率的进一步提高优化效果依然可以进一步提高.对于常用的8 b的加法，本文提出的基于斯格明子介质的全加器经过优化后只需要49个时钟周期即49 ns，相比基于磁畴壁的第1代赛道存储内存加法器 (8位加法需要108 ns)[1]快了2.2倍.

2.4 基于斯格明子逻辑门的乘法器

通常来说乘法可以分解为多次移位操作和加法操作，而本文提出的存内计算框架中全加器可以通过纯粹的基于斯格明子逻辑门实现，移位操作又是斯格明子纳米线器件自带的能力，因此本文提出如图7所示基于斯格明子逻辑门的8位乘法器.

在图7中，An代表当对应操作数B的第n位为1时，需要将操作数A左移n-1位.例如当操作数A和B的二进制形式分别为1101和111时，有A0=1101，A1=11010，A2=110100，此时A乘以B就等于A0+A1+A2.由于操作数A存储在斯格明子纳米线上，而纳米线器件本身就支持移位操作，因此An可以通过将操作数A左移n位得到，再直接输入全加器中得到乘法结果.因此基于斯格明子的乘法器可以通过重复利用已有的斯格明子全加器和本身的移位来实现，因此大大减少了计算逻辑单元所需的空间以及时间，同时也减少了实现存内计算框架的复杂程度.

Fig. 7 8-bit Skyrmion nanowire-based multiplier图7 基于斯格明子的8位乘法器

3 基于斯格明子介质的存储单元设计

在存内计算框架中存储单元与计算单元一同对整个系统的性能起着至关重要的作用.而斯格明子-赛道型存储器本身的物理特性决定其与传统的DRAM存储器随机读写的方式并不相同，斯格明子-赛道型存储器具有顺序读写的特性.因此我们无法简单地用斯格明子存储单元直接替代DRAM存储单元.为了进一步提高斯格明子存内计算框架的效率，我们需要根据斯格明子-赛道型存储器的本身物理特性来从底层硬件及系统软件2个层面考虑存内计算框架中存储单元的设计.

Fig. 8 Skyrmion based memory cell 图8 基于斯格明子介质的存储单元

3.1 斯格明子存储单元底层硬件设计

基于斯格明子的基本存储单元具体结构如图8所示.其中存储部分由RT0到RT3共4条基本赛道组成.每条赛道上可能有n个读写端口(图8中圆形部分)，这样每个单元可以一次读写4n(单位为b).典型的赛道型存储器具有3个基本操作即读、写以及移位.由于其中移动数据的移位操作占据绝大部分的时间和能耗，所以如何在不影响系统性能的情况下尽量减少数据的移位操作是亟待解决的问题.

在图8所示结构中，减少移位最直观有效的方法是增加读写端口的数量.但是由于读写端口本身会占用大量的空间，因此增加读写端口会相应降低存储的密度，同时会带来读写延时、能耗的增加以及实现工艺的复杂化，因此需要在增加读写端口与减少数据移位之间寻找一个平衡点.同时每个基本存储单元由几条赛道组成，以及每条赛道的长度(即可以存储的数据量)是多少，都对整个读写单元的性能有着至关重要的影响.文献[10，13]经过大量实验分析得知在多数应用中，每个基本存储单元中由4个条带组成，每个条带存储64 b数据能取得较好性能.这时如果每条赛道的读写端口大于16，单个存储单元占用面积以及读写时延以及功耗都会急剧增加；而当读写端口数小于16时，单个存储单元占用面积随着端口数减少反而会增加，因为此时条带两端需要为移位操作预留的空间也越来越大.同时在后续的实验部分中，本文也分析了在本文提出的基于斯格明子的存内计算框架下读写端口的数量与移位操作数的相应变化，综合考虑我们选择读写端口为16.

3.2 斯格明子存储单元系统优化

由于斯格明子-赛道型存储器不同于传统的DRAM存储器具有顺序读写的特性，因此传统的为随机读写存储器设计的系统地址映射方式并不适用于这种新型的非易失性存储器.图9(a)所示为传统的DRAM的地址映射方式RBC(row bank column)，这种存储系统通常使用一种典型的开放式页面地址映射策略，将所有相邻列的同一行映射到一个连续的区域，使空间局部性最大化.同时，它通过行列交织的方式来管理流水线式的内存请求.

对于斯格明子-赛道型存储器来说，关键问题是传统地址映射方式将每个行作为一个连续区域而不考虑移位的问题，也不考虑这些行可能横跨了许多不同内存存储单元，因此可能会带来非常严重的负面效应.如图10所示，256行依次分布在第1存储单元MC1到第64存储单元MC64，为了简化讨论，假设内存中有64个基本存储单元，每个存储单元只有1条存储赛道，每条赛道只能存储4 b数据且只有1个读写端口.在传统的地址映射方式下由于内存访问都具有很高的空间局部性，导致内存访问可能在不同存储单元之间以及存储单元内部频繁切换.在图10的例子中，应用程序的内存访问序列为R4→R8→R1→R4→R6.这些请求只映射到2个相关存储单元(MC1，MC2)，从而导致了多次移位操作(总移位为14次).考虑到基于斯格明子的存储器存储密度极大化以及内存访问的局部性，再结合存内计算的具体应用场景，本文提出了一种新的地址映射方式,即基于斯格明子介质的地址映射方式(address mapping based on Skyrmion, AMBS).

Fig. 10 An example of using AMBS图10 使用赛道型地址映射的优势1例

我们首先解释这种地址映射方案如何具体实现.AMBS将地址位(第16 b到第31 b)分为3部分：SN，PN，MN，见图9(b).其中SN(shift number)表示初始行和其对应访问端口的距离，即初始数据需要移位多少次才能够被访问.PN(port number)表示的是访问数据对应的端口序列号，即通过第几个端口去访问数据.MN(memory cell number)表示基本存储单元的编号.具体地说，如果每个x位数据共享一个端口，即要将内存中所有的行地址按照SN的数值划分为x组，并将地址相邻的行划为同一组. AMBS策略优先在组内进行数据分配，只有组内整个空间分配完之后，才将后续数据分配给下一组.

通过这种赛道型内存地址映射方式可以极大地减少移位操作，原因主要有2方面：1)在组间来说，假设内存的总容量为8 GB，每32 b数据共享一个端口，此时每组的大小为256 MB(8 GB/32)，此时由于内存读取的局部性，内存访问序列有极大可能属于某一组，因此可以减少由于较小区域的空间局部性导致的频繁移位操作.2)在组内来说，由于延迟和能耗主要来自于移位操作，特别是长距离的移位操作，因此减少移位的距离也能提高系统性能.而赛道型内存地址映射能将大部分内存读写的移位操作距离减少至1，这是因为同一存储单元中相邻2行的地址差距非常大(256 MB).

结合上述说明，我们以图10为例来说明AMBS是如何工作的.内存访问序列为R4→R8→R1→R4→R6，在传统的内存映射方式下，需要14次移位操作才能够读取完这些数据，而在基于赛道内存的操作下不需要进行任何移位任何操作就能完成内存数据的读取，节省了大量时间和能耗的开销.而赛道型内存地址映射方式的实现方式，可以通过在操作系统中使用一个统一的分系统管理物理页，并形成了一个层次结构基于Shift和Port的可用页面列表，类似于页面着色技术[17]，根据应用程序需要的不同存储容量，尽可能地分配一个连续的区域.因此最简单的方式，可以使用一个静态的物理地址的映射系统，在内存控制器中或斯格明子-赛道型存储器芯片内部实现.这样就可以在不改变现有操作系统的存储器体系接口下实现，因此带来的额外开销也基本可以忽略.

4 实验与结果分析

本节分别从硬件层和系统层对基于斯格明子介质的存内计算单元进行性能评估.首先对于硬件层面，探讨了基于斯格明子逻辑门的存内计算单元的性能，其次在系统层面上通过通用的图像锐化程序对于内存存储单元的读写端口个数与数据移位操作数的关系，以及整个存内计算系统的时间及能耗效率进行了评估.

4.1 基于斯格明子的计算单元性能评估

斯格明子逻辑门组成的基本运算单元作为存内计算框架的基础，首先我们需要对其性能进行评估.本实验中所用的斯格明子器件的读写时间与能耗数据来自于文献[18]，同时移位操作的能耗可以通过斯格明子纳米线的热耗散数据计算得出，移位操作的时间可以通过斯格明子在纳米线上的移动速度计算得出.需要注意的是当斯格明子逻辑门的工作状态即输入不同时，纳米线上的驱动电流密度也会随之变化[14-15].例如当逻辑与门的输入为0和1时(即只有一个斯格明子进入与门)，电流密度为7×1012A/m-2；当逻辑与门的输入为1和1时(即有2个斯格明子同时进入与门),电路密度为4×1012Am-2，因此在计算整个计算单元的功耗时我们只能取其平均值.在斯格明子逻辑门中使用的纳米线长约为600 nm，宽度约为100 nm[14]，由此我们可以计算出计算单元占用的面积.基于斯格明子计算单元对比基于磁畴壁计算单元极大地减少了额外COMS电路的使用，不仅使得性能上有所提高，也极大地减少了实现工艺所需的复杂度.

表1中对比了基于斯格明子计算单元和基于磁畴壁计算单元在时间、能耗和面积上的区别.可以看出，本文提出的基于斯格明子的存内计算单元相比目前最先进的基于磁畴壁的存内计算单元节省了54.6%的时间、42.9%的能耗以及23.1%的占用面积.这主要归功于斯格明子介质优异的物理性质：加法计算单元进行的优化，以及乘法计算单元对于加法器的复用.同时相比基于磁畴壁计算单元，大大减少了外围辅助电路的需求，简化了电路设计，使得基于斯格明子计算单元更容易被实现.

Table 1 Performance Comparison of TwoComputing Units

4.2 基于斯格明子的存内计算框架性能评估

4.2.1 实验环境配置

为了更准确评估基于斯格明子的存内计算框架的总体性能，本文采用调整过的基于磁畴壁的存内计算框架[1]来作为比较对象.为了模拟应用程序在存内计算框架中的具体执行过程，我们修改了体系结构模拟器Gem5[19]中内存部分，同时为了获得具体时间和能耗数据，我们结合了功耗和时序建模工具McPAT[20]建立了整个实验平台.

表2列出了实验中的主要参数配置.其中存内计算框架中主存储单元均被设置为1 000 MHz，与计算单元保持同步.对于基于磁畴壁的存内计算框架，时间和能耗参数可以从扩展的NVSim[21]中获取.由于本文提出的内存框架具有加法器和乘法器组成的计算单元，因此理论上任何程序中的加法和乘法操作均可以在此内存框架中完成.特别地,本文选取了主要操作均由加法和乘法组成的图像锐化程序作为实验测试程序，并在4.2.2节中介绍了图像锐化程序的具体执行过程.

Table 2 Configuration Parameters of Experiment表2 实验环境中关键参数配置

4.2.2 基于存内计算框架的图像锐化程序实例

为了详细说明程序是如何在基于斯格明子的存内计算框架中执行的，以及存内计算带来的优势，本节以图像锐化处理为例详细描述程序执行过程.

Fig. 11 The working process of image sharpening in PIM architecture图11 图像锐化程序在存内计算框架中具体执行过程

图像锐化即加强图像中重要信息，使得图像更清晰、更易于处理，在图像处理识别等各个领域都起着非常重要的作用.由于其处理的对象是以矩阵的形式将对应像素点信息存储于内存中的数字化图片，涉及到大量的矩阵操作，特别适合于用PIM进行并行处理.其本质是利用微分等运算加强图像中包含边缘信息的高频部分，代表性算法为拉普拉斯算子.拉普拉斯算子是一种二阶微分算子，一个连续的二元函数f(x,y)其拉普拉斯运算定义为

(1)

对图像处理来说，可以将拉普拉斯算子简化为

g(i,j)=4f(i,j)-f(i+1,j)-f(i-1,j)-

f(i,j+1)-f(i,j-1).

(2)

在数字图像处理中即表示将某个点对应像素的数值乘以4再减去其上下左右相邻像素对应的数值.在图像锐化处理的过程中，拉普拉斯算子可以直接通过模板操作来实现，即用拉普拉斯模板与图像中对应像素数值矩阵进行点乘来得到锐化后的图像数值.如图11所示，其中常用的模板为

(3)

图11以使用拉普拉斯算子模板进行图像锐化的程序为例，说明通用程序在基于斯格明子介质的存内计算框架中执行过程.如图11所示，基于斯格明子的存内计算框架主要包含存储单元和计算单元2部分.

其中存储单元部分由斯格明子-赛道型存储器组成，如图11上半部分所示，灰色部分表示读写端口所在位置.在未使用AMBS策略之前读取2个矩阵的数据需要进行多次移位操作，而在使用AMBS策略之后数据均存储在读写端口的位置，读取这些数据不需要再进行任何移位操作.图11中计算单元部分由基于斯格明子的乘法器(S-MUL)和加法器(S-ADDER)等逻辑运算单元构成.同时存内计算框架不同于传统的使用外部处理器的计算框架，在内存中还应设有专门的控制器来控制程序的执行过程.如图11下半部分所示，图像锐化程序的执行过程可被分解为4个主要步骤：

步骤1. 指令输入.此时控制指令由外部处理器输入到内部的控制器.包含需要处理的数据地址、需要进行的数据处理操作等.在如图11所示例子中即包含存储图片对应像素信息的3×3矩阵的地址、存储拉普拉斯模板矩阵的地址以及需要进行的对应矩阵元素的加分和乘法操作.

步骤2. 取数据.内部控制器根据指令从存储单元对应地址处取出数据，在图11中为一个保存图像像素信息的3×3矩阵以及一个存储拉普拉斯算子模板信息的3×3矩阵.

步骤3. 数据处理.控制器将相应数据分配至各个逻辑运算单元进行数据处理，直至得到需要的结果.图11中进行的是像素与模板的乘法，即2个矩阵的点乘运算.首先将对应矩阵按行、列进行分解，如图11中分解成(5，21，8)与(0，-1，0)；再将对应数值输入相应的基于斯格明子的乘法器分别得到(0，-21，0);最后将结果通过基于斯格明子的加法器多次相加得到最终结果(2).

步骤4. 数据写回.最后将处理的结果(2)再写回到存储单元中.

上述过程不断重复，直至将整个图像的数据进行类似的卷积操作之后，就可以得到锐化后的图像.在这个过程中，图像数据均不需要传输到外部处理器进行处理，从而节省了大量的时间和能耗.

4.2.3 实验结果

本实验主要分为2部分：第1部分主要分析读写端口数与移位次数之间的关系，以确定在斯格明子-赛道型存储器中基本存储单元读写端口数；第2部分将本文提出的基于斯格明子的存内计算框架与目前最先进的基于磁畴壁的存内计算框架进行对比.

如图12所示，我们首先研究了存储单元读写端口对程序执行过程中赛道型内存总移位数的影响.为了便于比较，将总移位以Base-16为基准进行规格化.其中Base-X代表不使用AMBS内存映射策略且每个内存单元具有X个读写端口的情况，AMBS-X指的是使用AMBS映射策略且每个内存单元具有X个读写端口的情况.可以看出，使用AMBS内存映射策略之后移位操作次数极大减少.这主要是由于：1)AMBS映射策略使得同一张图片的数据均被存储在同一组具有相同SN的内存中，因此图片锐化程序读取1张图片数据时就不再需要进任何移位操作；2)AMBS映射策略使得相邻图片的数据存储在同一组或者相邻组内存中，在这种情况下读取相邻图片数据的图片也最多需要进行一次移位操作.同时我们还可以从图12中看出,AMBS-16与AMBS-32差距较小，而与AMBS-8差距较大.这是由于AMBS-16位移操作次数已经较少，再增加端口数也无法大幅减少位移操作次数，但是减少端口数会显著增减位移操作的次数.综上所述，结合占用面积、读写延时等情况考虑，单个基本存储单元读写端口为16时能取得较好性能.

Fig. 12 The impact of the read/write ports on the shift operation compared with Base-16图12 与Base-16对比读写端口对移位操作数影响

在实验的第2部分，我们使用通用的图像锐化程序作为实验程序，同时为了使得实验结果更具有通用性，我们使用一系列不同分辨率的图片集作为实验比较对象.

图13对比了在不使用AMBS策略(Without AMBS)与使用AMBS策略(With AMBS)的情况下，基于斯格明子的存内计算框架与基准性能(基于磁畴壁的存内计算框架)的比较.可以计算得出，使用AMBS策略与不使用AMBS策略相比，存内计算框架平均能节省4.5%的时间和8.7%的能耗.容易观察到，系统整体性能的差距要比图12中位移次数的差距小得多.这主要是因为在基于斯格明子的存内计算框架中计算单元占据了大部分的时间和能耗.同时我们也注意到当测试图片逐步增大时，时间和能耗的减少比例也逐步扩大并趋近一个极限值.这是由于随着数据量的不断增加，斯格明子内存框架内程序运行的并行程度也在不断提高并接近其极限.因此在一定范围内，斯格明子存内计算框架中程序处理的数据量越大越能获得更多优势.

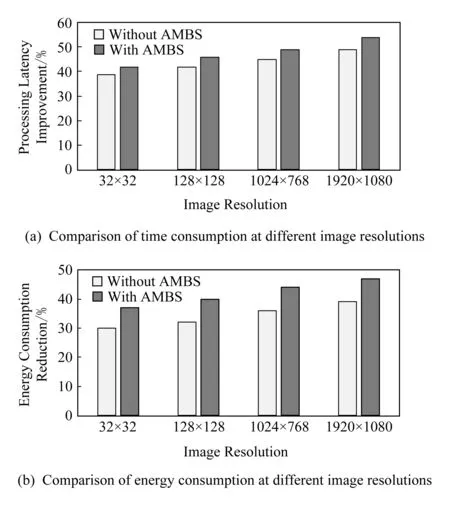
Fig. 13 Performance evaluation of PIM architecture based on Skyrmion图13 基于斯格明子的存内计算框架性能评估

从总体上来说，实验结果表明:在不使用AMBS映射策略下，本文提出的基于斯格明子的存内计算框架相比目前最先进的基于磁畴壁的存内计算单元在时间上平均节省了43.6%，在能耗上平均节省了34.2%.在使用了AMBS映射策略之后，平均节约时间上升至48.1%，同时平均节约能耗42.9%.

5 总 结

本文提出了基于斯格明子逻辑门的加法和乘法计算单元，探讨了斯格明子基本存储单元的设计方式，优化了斯格明子存储单元的地址映射方式，并最终在此基础上建立了基于斯格明子介质的存内计算框架.本文提出的存内计算框架在获得基于斯格明子-赛道型内存的非易失性存储单元优势的同时又获得了基于斯格明子逻辑计算单元的优势.在存储单元方面，本文首先从硬件层面探讨了斯格明子-赛道型存储单元的读写参数优化等问题，再从系统层面提出了基于斯格明子-赛道型存储单元专用内存映射策略，从而在总体上改善了存内计算单元的性能.在计算单元方面，本文提出的基于斯格明子的全加器和乘法器不仅受益于斯格明子本身优异的物理特性，同时计算单元的并行优化设计以及电路的复用也极大地提高了系统整体性能，降低了系统实现的复杂度.实验表明:本文提出的存内计算框架与目前最先进的基于磁畴壁的存内计算框架相比，在时间上平均节省了48.1%，在能耗上平均节省了42.9%.