大跨度板桁加劲梁悬索桥自振频率参数敏感性分析

张翼, 李永乐, 汪斌, 王磊

(西南交通大学 桥梁工程系，四川 成都 610031)

板桁加劲梁由正交异性板和桁架组合成一整体，协调受力，具有自重轻、极限承载力大、抗风稳定性好、跨越能力强等优点。随着近些年桥梁建设的高速发展，板桁加劲梁已成为大跨度桥梁常用的断面形式。采用板桁加劲梁的大跨度桥梁包括德国欧姆里希桥、加拿大狮门桥、平潭海峡公铁两用大桥和安庆铁路长江大桥等。目前，围绕大跨度板桁加劲梁悬索桥各国学者已做了大量的研究。郑宪政利用自编软件SBAP和SBEAP3对大跨度悬索桥加劲梁在架设过程中各个状态进行了静动力分析；刘忠平等建立大跨径自锚式悬索桥有限元模型，从恒载作用和主缆、吊杆内初张力等方面对自振模态进行了分析；何晗欣等利用Ansys有限元软件分析了抗风缆和中央扣等结构对大跨窄钢桁架加劲梁悬索桥抗风性能的影响；美国学者利用SAP2000程序建立了塔科马新桥板桁加劲梁节段的精细化有限元模型，分析了加劲梁的剪力滞效应；苏茂材利用Ansys有限元软件分析了大跨度斜拉桥桁宽和桁高等敏感参数对桥梁动力行为的影响。

但针对大跨度板桁加劲梁悬索桥动力性能的参数敏感性研究还相对欠缺，板桁加劲梁的各组成构件对结构动力特性的影响研究还很少。桥梁抗风研究中，动力特性影响结构的抗风稳定性，控制结构的颤振性能。同时动力特性是桥梁抗震和车桥耦合分析的基础，也是其他动力分析(如反应谱分析)的根本。因此对大跨度板桁加劲梁悬索桥动力特性进行参数敏感性分析具有重要意义。该文以一座大跨度板桁加劲梁悬索桥为背景，建立精细化有限元模型计算动力特性，并选取6种结构参数针对自振频率的敏感性进行分析。

1 工程背景

研究对象是为度1 386 m的单跨双塔板桁结合式悬索桥，为目前西部山区在建最大主跨桥梁。主缆成桥状态垂跨比为1/10，理论矢高为138.6 m，缆中心距为27.0 m。加劲梁包括钢桁架和桥面板两部分，板桁结合，共同承担荷载。

桥面板采用正交异性板，顶板厚度16 mm，U肋厚度8 mm。钢桁架桁宽27.0 m，桁高9.5 m，节段长度10.8 m，主要包括主桁架、横桁架和下平联，其立面图和平面图分别见图1、2。主桁架由弦杆、竖腹杆和斜腹杆组成，横桁架由横梁、竖腹杆和斜腹杆组成，所有钢桁架杆件均采用箱形设计。主桁架采用两片主桁架的方式，上主桁杆横向通过桥面板整体组合式连接，下主桁杆横向通过下横梁及下平联连接，其中下平联采用K形连接的方式。

图1 主桁立面图(单位：m)

图2 主桁平面图(单位：m)

2 精细化有限元模型及动力特性

采用Ansys软件建立全桥精细化有限元模型，韩万水等对大跨钢桁架悬索桥进行分析时采用Beam4单元和Link10单元分别模拟主梁和主缆；张文明等同样只采用梁单元和杆单元对悬索桥进行精细化分析。但针对板桁结构，梁单元不能精确模拟桥面板的受力特点，无法反映桥面板和U肋等对桥梁动力行为的影响效应。因此为了更加精确地对板桁结构进行动力特性参数分析，此次建模中钢桁架采用Beam4梁单元模拟，主缆和吊索采用Link8杆单元模拟，正交异性桥面板采用Shell63壳单元模拟。Shell63单元为弹性壳单元，既具有弯曲能力又具有膜力，可以承受平面内荷载和法向荷载，不仅可以模拟U肋等构造，而且可以很好地模拟桥面板的受力特点，使计算结果更加可靠。

精细化有限元模型中钢桁架部分共采用梁单元4 636个，桥面板部分共采用板单元356 728个。图3为全桥的有限元模型，图4为板桁加劲梁的局部模型。通过动力特性计算分析得到该桥的1阶正对称、反对称横弯振型频率分别为0.052 3、0.134 2Hz、1阶正对称、反对称竖弯振型频率分别为0.147 3、0.093 5Hz、1阶正对称、反对称扭转振型频率分别为0.291 4、0.329 0 Hz。该桥基频为正对称横弯，说明桁架结构的桥梁横向刚度较小。基频值为0.052 32 Hz，符合一般大跨度悬索桥的频率规律。

图3 有限元模型

图4 板桁加劲梁局部模型

3 加劲梁构件参数敏感性

针对板桁加劲梁的构造特点，以建立的精细化有限元模型为基础，分析桥面板参数以及桁架参数对桥梁动力特性的影响，参数主要包括桥面板厚度、U肋厚度、主桁斜腹杆截面积、下平联斜腹杆截面积、弦杆截面积及下横梁截面积，通过主要振型(1阶横弯、1阶竖弯、1阶扭转)频率的变化来反映各参数的影响。

3.1 桥面板厚度变化

该桥桥面板厚度为16 mm，以此为基准，分别取桥面板厚度为12、14、18和20 mm进行比较分析。桥面板厚度变化对板桁加劲梁动力特性的影响见图5。

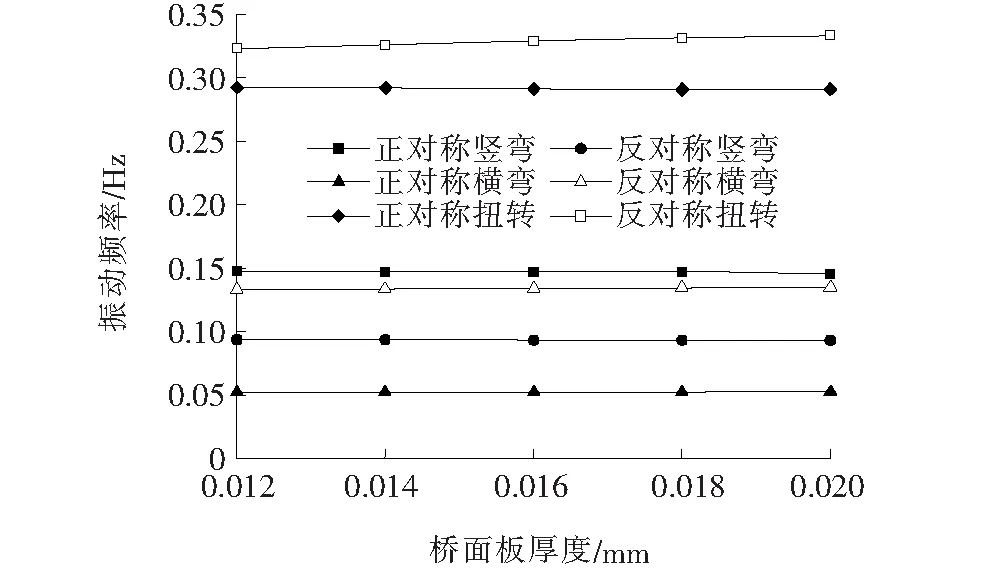
图5 桥面板厚度对基频的影响

由图5可知：总体上随着桥面板厚度的增加，桥梁横弯频率增加，竖弯频率减少。当厚度由12 mm变化到20 mm时，1阶正对称与反对称竖弯频率分别减少了0.37%和0.58%，而1阶反对称横弯频率却增加了1.29%。桥面板厚度的增加使1阶正对称扭转频率有减小的趋势，对1阶反对称扭转频率的增加影响最明显，但变化幅度也只达到3.30%。桥面板作为正交异性板的组成部分，承担并传递荷载才是最主要的作用。因此桥面板厚度的设计主要是满足受力要求，不用考虑通过桥面板厚度的变化来优化板桁加劲梁结构的动力性能。

3.2 U肋厚度变化

U肋作为纵向加劲肋能够提高桥面板的刚度，同时也是板桁结构的一部分，因此研究U肋对整体板桁结构动力性能的影响很有必要。以U肋的设计厚度8 mm为基准，分别改变厚度为6、7、9和10 mm，进行桥梁的动力特性分析，得到U肋厚度变化对结构动力特性的影响如图6所示。

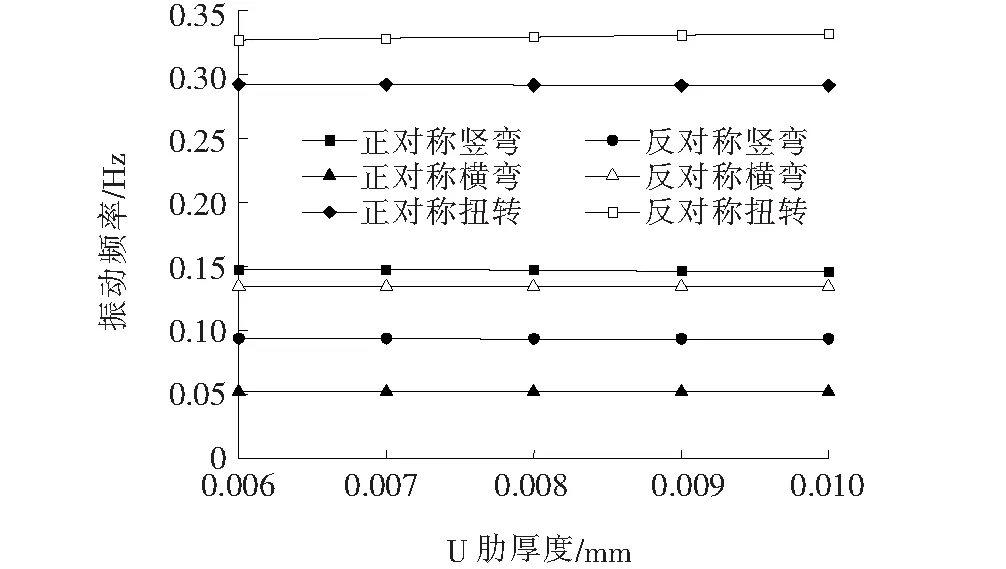
图6 U肋厚度对振动基频的影响

由图6可知：桥梁的1阶反对称扭转频率随着U肋厚度的增加而增加，当U肋厚度从6 mm增加到10 mm时，1阶反对称扭转频率增加了1.53%。桥梁的其他主要振型频率的变化规律则完全相反，随着U肋厚度的增加，桥梁的竖弯振型频率、横弯振型频率以及正对称扭转振型频率呈现减小的趋势，减小幅度最大的振型为1阶正对称竖弯，但也仅仅减小了1.06%。因此可以认为U肋厚度对桥梁整体动力性能基本没有影响，设计U肋时不需要考虑整体的动力效应。

3.3 主桁斜腹杆截面积变化

该桥设计中主桁采用的是华伦式结构，其中斜腹杆可受拉也可受压，与弦杆一起组成主桁，是桁架的主要受力构件。主桁斜腹杆对结构动力特性的影响效应，通过改变斜腹杆截面积的方式进行分析，结果如图7所示。

由图7可知：主桁斜腹杆截面积的变化对桥梁动力特性的影响很小。当截面积由0.021 m2增加到0.037 m2时，桥梁的竖弯振型和横弯振型的频率都有减小的趋势，但均未超过1%；扭转振型频率呈现增大的趋势，其中1阶反对称扭转频率增幅最大，达到了1.23%，1阶正对称扭转频率增幅未超过1%。因此可以认定板桁加劲梁结构中主桁斜腹杆截面积的变化对桥梁结构的动力特性几乎没有影响。

图7 主桁斜腹杆截面积对振动基频的影响

3.4 下平联斜腹杆截面积变化

下平联斜腹杆作为横向联结系的一部分，主要是传递横向水平力。此次设计中下平联斜腹杆截面积为0.023 m2，分别取截面积为0.015、0.031、0.039和0.047 m2，计算结构的动力特性并进行参数敏感性分析，得到结果如图8所示。

图8 下平联斜腹杆截面积对振动基频的影响

由图8可知：下平联斜腹杆截面积的变化对横弯振型和竖弯振型的频率几乎没有影响，但是对扭转振型的频率影响十分明显。当截面积由0.015 m2增加到0.047 m2时，1阶正对称扭转频率增加了11.2%，1阶反对称扭转频率增加了9.18%。因此当需要优化板桁加劲梁结构扭转频率时，可考虑通过改变下平联斜腹杆的截面积来改变扭转频率，从而优化结构的动力性能。

3.5 弦杆截面积变化

弦杆作为桁架的主要组成部分，可分为上弦杆和下弦杆，与腹杆一起构成主桁架。弦杆作为主要构件，也需要考虑其对桥梁动力性能的影响。此次设计中弦杆截面积为0.078 m2，通过计算不同弦杆截面积下的动力响应，得出弦杆对结构动力特性的影响见图9。

图9 弦杆截面积对振动基频的影响

由图9可知：弦杆截面积的增加会使桥梁的竖弯振型和横弯振型的频率呈现增加的趋势，其中对1阶反对称横弯的影响最明显。当弦杆截面积由0.062 m2增加到0.110 m2时，1阶反对称横弯频率增加了7.6%，1阶正对称横弯频率增幅为2.9%。1阶正对称竖弯频率和1阶反对称竖弯频率增幅也能达到2%。但弦杆截面积的变化对扭转振型频率的影响有不同的趋势，当弦杆截面积增加77%时，1阶正对称扭转频率减少了3.97%，但1阶反对称扭转频率却增加了2.16%。因此可以认为弦杆截面积的改变对桥梁结构的动力特性有明显影响，特别是对1阶反对称横弯频率和1阶正对称扭转频率的影响较大。

3.6 下横梁截面积变化

下横梁的设置能够增加桁架的横向刚度，提高整个桁架结构的受力性能。通过改变下横梁截面积来分析其对结构动力特性的影响，得到结果如图10所示。

图10 下横梁截面积对振动基频的影响

由图10可知：下横梁截面积的变化对结构的振动频率没有明显影响。当截面积由0.026 m2增大到0.058 m2时，振动频率变化最大的振型是1阶反对称横弯，但也仅仅是减少了1.6%。因此可以认为下横梁截面积的变化对结构的动力特性没有影响。

4 结论

(1)在大跨度板桁加劲梁悬索桥中，桥面板厚度和U肋厚度的变化对结构动力特性基本没有影响。桥面板和U肋作为正交异性板的组成部分，尺寸变化导致的板桁加劲梁动力特性的改变很小。

(2)通过参数分析发现，主桁斜腹杆截面积和下横梁截面积的变化对板桁结构动力特性没有明显影响。两者只需考虑作为桁架结构的组成部分参与全桥的受力即可，对动力特性影响小。

(3)根据参数敏感性分析发现：在板桁加劲梁悬索桥中，下平联斜腹杆截面积的变化对板桁加劲梁1阶正对称扭转频率和1阶反对称扭转频率的影响十分显著；弦杆截面积的变化对板桁加劲梁1阶反对称横弯频率有明显影响，对1阶正对称扭转频率有相反趋势的影响。因此在设计中可以通过对两项参数的优化调整，使板桁加劲梁悬索桥动力性能达到最佳。