基于非线性M-C准则的圆形基础下伏土洞抗冲切破坏研究
2019-04-16王志斌罗谢鑫夏浩祥
王志斌,罗谢鑫,夏浩祥
基于非线性M-C准则的圆形基础下伏土洞抗冲切破坏研究
王志斌,罗谢鑫,夏浩祥
(湖南科技大学 土木工程学院,湖南 湘潭 411201)
针对土体材料特点,引入非线性Mohr-Coulomb准则及相关流动法则,构建圆形刚性基础下伏土洞冲切破坏模式。采用极限分析上限法推导出其极限承载力的计算公式,得出参数任意组合条件下圆形刚性基础下伏土洞冲切极限承载力。利用Plaxis 3D软件建模分析,并与理论解进行对比,验证本文方法的有效性。研究结果表明:非线性系数对极限承载力的影响较大,在其他参数条件一定的情况下,极限承载力与呈非线性负相关,且趋于稳定。极限承载力随土体初始黏聚力0,顶板厚度以及刚性基础宽度的增大而增大,随土体重度、土体抗拉强度的增大而减小。
非线性Mohr-Coulomb准则;极限分析;极限承载力;圆形基础;冲切
我国岩溶地质分布范围广泛,土洞是发育于可溶岩层上覆土体内的空腔,是岩溶区常见的一种岩溶作用产物[1]。在一些冲积区,第四系土层覆盖厚度较大,可达40余米,土洞深埋于第四系土层中[2]。当桩基或独立基础位于土洞或软弱下卧层上方时,常产生冲切破坏[3]。目前国内外研究重点在于岩溶区桩基抗冲切破坏模式,Hongseob等[4]得出混凝土和岩石等脆性材料在受冲切作用破坏时的冲切破坏体并非标准的圆锥台形,而是以一定曲线为母线所形成的轴对称旋转体。赵明华等[5−6]通过将溶洞简化为梁板结构模型,系统地研究了溶洞顶板的稳定性与安全厚度;张慧乐等[7−8]采用室内模型试验的方法,研究了岩溶区嵌岩桩的承载能力与破坏模式,得出嵌岩桩破坏模式和影响因素;刘善军等[9]基于应力平衡法建立了松散盖层稳定性计算公式。曾中林等[10]采用变分法对岩溶区条形刚性基础下伏孔洞岩体冲切破坏机制进行了研究。雷勇等[11]采用变分法得到岩溶区桩端岩层抗冲切安全厚度计算公式。这些研究指明了地下空洞变形破坏的方向。通过对以上研究现状的总结发现,以往研究对象多集中在岩溶,以岩质材料为主,对土质材料形成的孔洞承受地表荷载的研究甚少。本文采用极限分析上限法,构建圆形刚性基础下伏土洞破坏模式,根据非线性Mohr-Coulomb准则及相关流动法则,推导出其极限承载力的计算公式,在此基础上采用数学软件Matlab进行编程求解,得出非线性Mohr-Coulomb屈服准则[12−17]参数任意组合条件下圆形刚性基础下伏土洞冲切极限承载力,利用Plaxis 3D软件建模分析,并与理论解作了对比,两者吻合较好,验证了本文方法的有效性,具有较强的理论与实践意义。
1 基本理论
极限分析上限定理:对于任意一个有效破坏机构,假定存在1个同时满足速度边界条件和应变−速度相容条件的速度场,根据外荷载功率等于内部能量损耗率的关系条件,能够得到1个不小于实际破坏荷载的极限荷载。具体如式(1)所示。

2 刚性圆形基础下伏土洞冲切上限分析
2.1 水平圆形刚性基础下伏土洞冲切破坏模型计算假定
根据极限分析上限定理,对于任意假定的冲切破坏机制,其速度场必须满足机动容许的要求,即满足如下条件:1) 速度边界条件;2) 几何相容条件;3) 相关联流动法则。通过虚功原理的功率平衡方程,解得的承载力为实际承载力的一个上限解。
由于极限分析上限定理是建立在将土体假想为理想的弹塑性体和忽略了其几何变形的基础上,故在构建破坏模式时作如下假设:1) 圆形刚性基础受冲切作用时,基础下覆土体为理想的弹塑性介质,破坏时服从非线性M-C强度屈服准则及相关流动法则;2) 基础下部的破坏土体为刚性体,且破坏过程中不与刚性基础发生相对滑动;3) 圆形刚性基础直径为2,下覆土层的厚度为,冲切破坏半径为,下伏土洞顶部支护力为。
为求得土洞区圆形刚性基础下覆土体受冲切作用时的极限承载力,必须先假定一种冲切破坏机制。为了使获得的上限解尽可能接近真实解,假定的冲切破坏机制还必须与圆形刚性基础下覆土体的实际破坏模式相同。Hongseob等[4]得出混凝土和岩石等脆性材料在受冲切作用破坏时的冲切破坏体是以一定曲线为母线所形成的轴对称旋转体。这是由于混凝土与岩石等材料的强度屈服准则往往具有非线性的特点,材料破坏面上应力分布不均,从而导致破坏面母线为曲线形式。
根据极限分析上限定理和冲切破坏体自身的特点,构建了图1所示的冲切破坏机制,并对其进行了相应假定:
1) 圆形刚性基础顶部受力的作用时传递到基础底部的作用为圆形均布荷载,破坏时呈三维轴对称破坏,且破坏场与基础对称轴重合。
2) 冲切破坏面方程开始于刚性基础端部边缘,在土体内部连续,其破坏面的母线几何方程为()。
3) 圆形刚性基础下覆土体为理想均质弹塑性体,破坏时服从非线性MC强度屈服准则。
4) 圆形刚性基础在达到极限状态时,下覆土体内部产生的塑性变形必须满足相关联流动法则的要求。

图1 圆形刚性基础三维冲切破坏机制
2.2 水平圆形刚性基础下伏土洞冲切极限承载力变分分析
2.2.1 水平圆形刚性基础下伏土洞冲切三维破坏机制的构建
假设圆形刚性基础下覆土体为理想均质弹塑性体,破坏时服从非线性Mohr-Coulomb屈服准则,刚性基础与土体之间无相对位移,圆形刚性基础极限状态下对应的三维曲线型破坏机制构建过程如下:首先假设有一条关于轴对称的速度间断线(),()自基础底部开始向下,直至土洞顶部,形成一个上部窄而下部宽的破坏面;其次令()绕轴旋转180°,形成一个“漏斗”型的冲切破坏体;该冲切破坏体由半径分别为和的圆和以()为母线的旋转曲面组成。该冲切破坏体的体积和侧表面积均可用解析数学的方法求解,在极限分析上限定理的能耗计算中,可以根据冲切破坏机构的体积和侧表面积算出其破坏机制的内能耗散功率于外力功率。
2.2.2 水平圆形刚性基础下伏土洞冲切能耗计算
将刚性基础下覆土体冲切破坏速度间断面视为薄变形层,其厚度为,作用在变形层上的剪应力为τ,正应力为σ,满足非线性M-C强度屈服准则。屈服函数可表示为:

在主应力空间内,令塑性势函数面与强度屈服面重合,根据相关流动法则,可得塑性势函数为[10]:

根据塑性位势理论[10]:
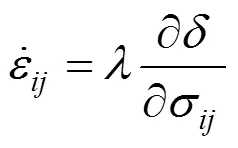
则将式(3)代入式(4)中可得分离薄层上的塑性应变率为:

根据图1中几何运动关系,可得:
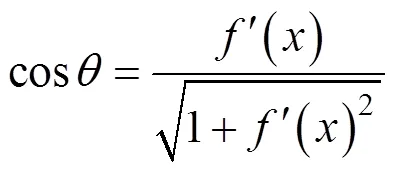
冲切破坏体分离薄层上的塑性应变率也可表示为:
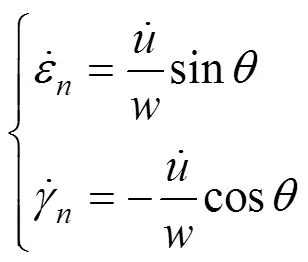
将式(6)代入式(7)中可得:

为满足变形的相容协调,式(5)和式(8)中的塑性应变率分量应相等,故可得分离薄层上的正应力分量和剪应力分量:

冲切破坏时内部能耗仅发生在刚性基础下覆土体的破坏分离面处,故薄变形层上单位体积的耗散功率为:


冲切破坏时,破坏土体的侧面积可以按旋转体的侧面积公式得到:

将式(10)沿冲切破坏体侧面积积分可得速度间断面上内能耗散功率为:


冲切破坏时土体重力的功率为:
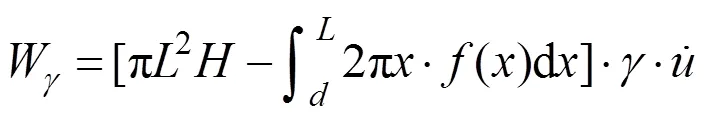
圆形刚性基础极限承载力的功率为:

圆形刚性基础下伏土洞洞顶支护力的功 率为:
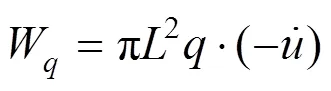
根据虚功率原理建立平衡方程,内能耗散功率等于外力功率,故有:

将式(12)~式(15)代入式(16)中可得圆形刚性基础冲切极限承载力的表达式为:


式中:
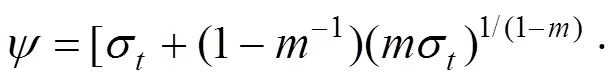

由极限分析上限法可知,求解结果大于真实的极限承载力,其最小值才更接近真实解。极限承载力的极值由式(17)所确定,通过变分运算可以将这一泛函的极值问题转化为求解欧拉方程在满足边界条件下的定解问题。对应的欧拉方程为[10]:

根据欧拉方程对()和()的偏导分别为:

将式(20)代入式(19)并整理可得:

式中:1为积分常数,可由如下边界条件求得。
由于冲切破坏时没有水平外力作用,且冲切破坏为对称破坏,故根据刚性基础端部微元体的平衡可知,水平剪应力分量τ=0。其表达式为:

其中:

故有:

将式(23)代入式(22)并由式(21)可得:

即:
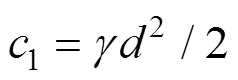
故有:
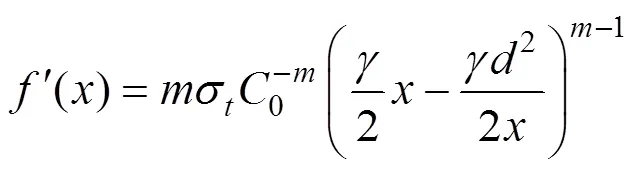
由式(27)可知,只有当−1是整数时,才能积分得到()的精确表达式,根据位移边界条件求得积分常数以及冲切破坏宽度,进而求得刚性基础下覆单层土体冲切极限承载力u的表达式。根据图1可知,位移边界条件如下:

式中:为下伏土洞冲切破坏宽度。
当其不是整数时,无法求得其原函数,但可根据差分原理并结合边界条件分层迭代得到()的函数曲线形状,同理,也可得到固定参数条件下极限承载力u的数值。
2.2.3 差分原理
为获求任意参数条件下圆形刚性基础下伏土洞冲切极限承载力,以下利用差分原理进行冲切破裂面曲线函数()数值求解,得到破裂面曲线函数()和旋转后的三维曲面形状,进一步分层积分迭加可以求得对应刚性基础极限承载力u。
根据差分法的基本概念:

给定式中参数,,σ,0和,可得出任意点x的导数值。假设曲线的每一微段为x+1−x=Δ,则将每点的导数值可视为点(x,(x))和点(x+1,(x+1))连接直线的斜率。将微小直线段近似为实际解析函数的曲线段,根据式(29)可得:
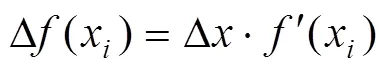
利用式(30)进行迭加计算,可得出每点的(x+1)值,其表达式为:
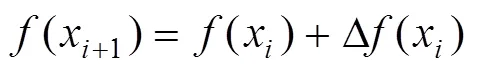
由于无法得到精确的解析曲线表达式,极限承载力u的求解采取同样的思路。首先得出每一微段直线对应的薄层极限承载力u()的积分表达式:

将全部的薄层极限承载力积分进行累加,可得整个破坏机构的极限承载力u的表达式为:

根据以上推导过程,利用数学软件Matlab进行编程求解,可得出非线性Mohr-Coulomb屈服准则参数任意组合条件下圆形刚性基础下伏岩溶土洞冲切极限承载力及其对应三维破坏模式。
2.3 圆形刚性基础下覆单层土体特殊分析模型
当=1.0时,非线性MC准则退化为线性Mohr- Coulomb准则,冲切破坏面退化为理想的圆台面,如图2所示。
由图2可知,破坏直线的斜率为:
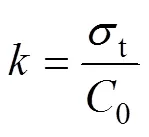
故其破坏直线的函数形式为:

式中:为待定系数,可由如下边界条件确定。

代入可得:

破坏直线方程为:
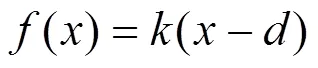
此时冲切破坏时内能耗散功率为:



图2 圆形刚性基础三维冲切直线破坏机制
土体重力的功率为:
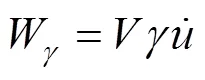
式中:表示破坏圆台的体积。

根据虚功率原理建立平衡方程可得:
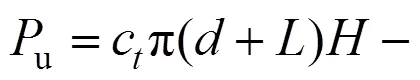

3 对比分析
采用Plaxis 3D建模进行对比分析。在半无限空间中,冲切破坏为圆对称破坏,故取1/4模型进行分析,如图3所示。模型边界尺寸20 m×20 m×20 m,圆形刚性基础半径=1 m,其上作用有均布荷载,即未知的极限承载力,土层厚度=5 m,孔洞半径=4.5 m,洞顶支护力=20 kN/m2,土体容重=18 kN/m3,土体黏聚力为=20 kPa,单轴抗拉强度t=30 kPa,非线性系数=1.0,内摩擦角=33.7°,杨氏模量=10 000 kN/m2,泊松比=0.3,不考虑水的影响。

图3 1/4模型图
利用Plaxis 3D软件进行塑性分析和安全性分析,通过在刚性基础上施加荷载,计算模型的安全系数,当计算得到的安全系数恰好为1时,此时的荷载为极限荷载。通过计算,得到的冲切极限承载力约为177 kN,安全系数s=1.002,其塑性剪切带三维图如图4所示。而本文基于极限分析上限定理所得冲切极限承载力为185.5 kN,孔洞破坏宽度约为4.33 m,其极限承载力和破坏宽度的误差分别为4.58%和3.93%,均不超过5%。同时,将剪切破坏带与理论解的破坏曲线作了对比,并将其展示在同一张图中,如图5所示,两者吻合较好,由此可说明本文方法的可行性和有效性。

图4 塑性剪切带

图5 三维破坏曲面剖面图
4 参数与破坏模式分析
由式(17)可知,影响圆形刚性基础土洞顶板的冲切极限承载力的因素众多。且非线性M-C准则的非线性系数对极限承载力的影响更为显著,以下分析土洞顶板自由冲切极限承载力随单一参数的影响变化情况以及破坏模式的变化。取刚性基础半径=0.5~1.5 m,土体抗拉强度t=40~60 kPa,土体初始黏聚力0=10~30 kPa,土体重度=16~24 kN/m3,顶板厚度=4~8 m,土洞顶板底部支护力=100 kPa,分别绘制出极限承载力随=1.0~3.0之间变化时的影响曲线。如图6~10所示。
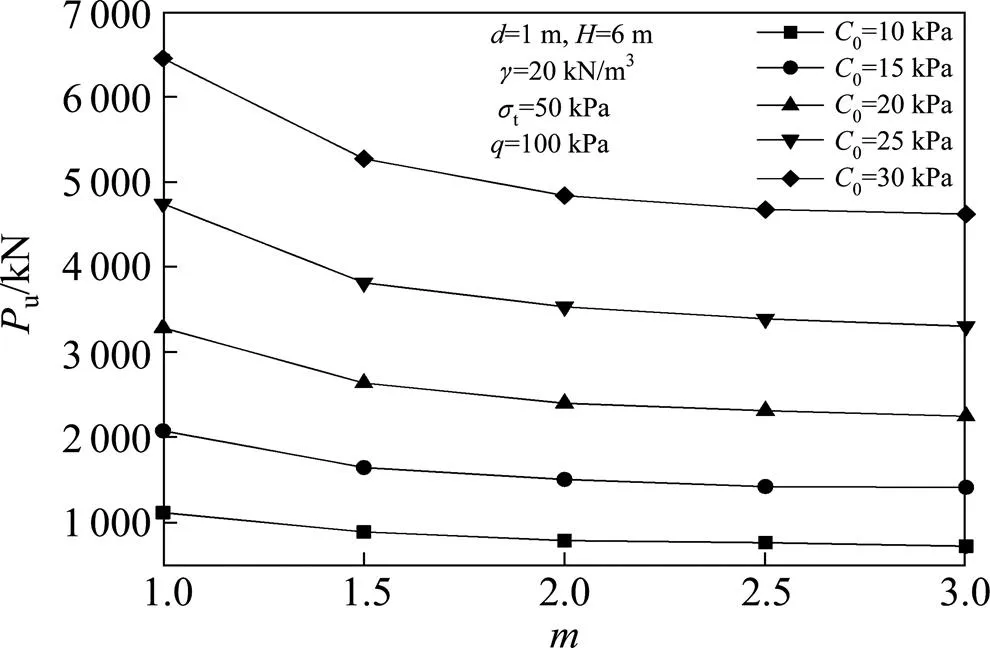
图6 Pu随C0变化曲线
综合图6~10可知,非线性系数对极限承载力的影响较大,在其他参数条件一定的情况下,极限承载力与呈非线性负相关,且趋于稳定。极限承载力随土体初始黏聚力0,顶板厚度以及刚性基础宽度的增大而增大,随土体重度、土体抗拉强度的增大而减小。

图7 Pu随d变化曲线

图8 Pu随γ变化曲线
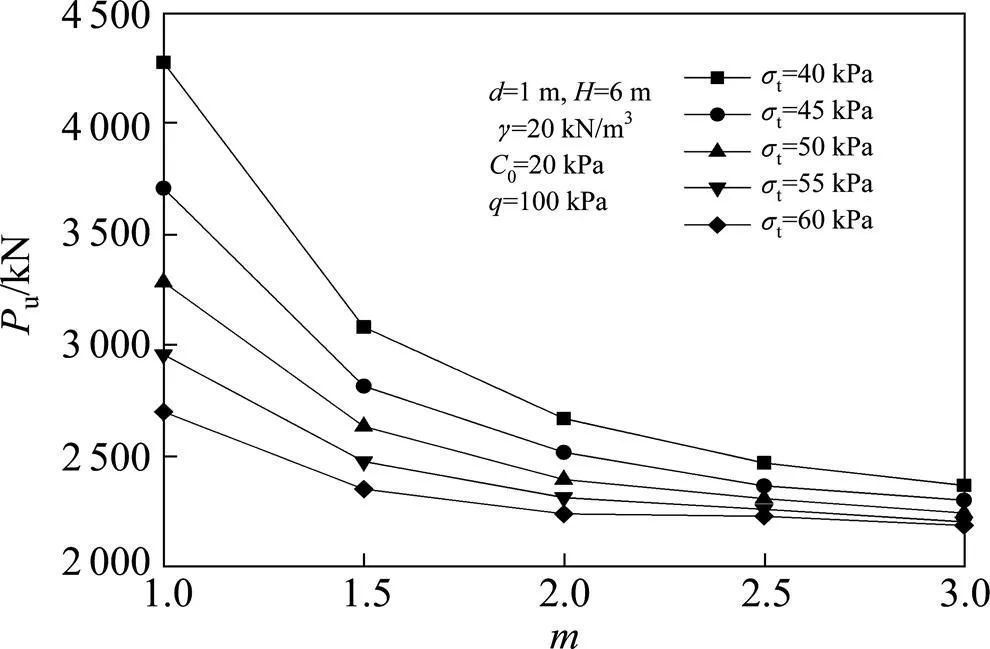
图9 Pu随σt变化曲线

图10 Pu随H变化曲线
5 结论
1) 根据非线性Mohr-Coulomb准则及相关流动法则,构造出圆形基础下伏土洞土体冲切破坏的机动速度场,利用极限分析上限法结合变分原理,推导出圆形刚性基础下伏土洞冲切破坏时的破坏曲面函数,利用差分原理结合边界条件迭代出破坏曲面函数形状及其极限承载力,拓展分析了圆形刚性基础下伏土洞冲切破坏时的特殊模型。利用Plaxis 3D软件建模分析,并与理论解作了对比,两者吻合较好,验证了本文方法的有效性。
2) 对于圆形刚性基础下伏土洞的冲切破坏,非线性系数对极限承载力的影响较大,在其他参数条件一定的情况下,极限承载力与呈非线性负相关,且趋于稳定。极限承载力随土体初始黏聚力、顶板厚度以及刚性基础宽度的增大而增大,随土体重度、土体抗拉强度的增大而减小。
[1] 刘镇, 黎杰明, 杨旭, 等. 考虑邻近土洞影响的盾构掘进速度控制[J]. 工程地质学报, 2017, 25(6): 1633− 1639.LIU Zhen, LI Jieming, YANG Xu, et al. Optimal control of TBM excavation rate considering neighboring soil void[J]. Journal of Engineering Geology, 2017, 25(6): 1633−1639.
[2] 丁春林, 甘百先, 钟辉虹, 等. 含土洞、溶洞的机场滑行道路基稳定性评估[J]. 岩石力学与工程学报, 2003, 22(8): 1329−1333. DING Chunlin, GAN Baixian, ZHONG Huihong, et al. Stability evaluation of airfield runway subgrade containing earth caves and karst[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(8): 1329− 1333.
[3] Wyllie D C. Foundations on rock[M]. London: Chapman and Hall, 1992.
[4] Hongseob O H, Jongsung S I M. Punching shear strength of strengthened deck panels with externally bonded plates[J]. Composites part B: Engineering, 2004, 35(4): 313−321.
[5] 赵明华, 张锐, 胡柏学, 等. 岩溶区桩端下伏溶洞顶板稳定性分析研究[J]. 公路交通科技, 2009, 26(9): 13−16. ZHAO Minghua, ZHANG Rui, HU Boxue, et al. Analysis of stability of cave roof under pile tip in karst area[J]. Journal of Highway and Transportation Research and Development, 2009, 26(9): 13−16.
[6] 赵明华, 雷勇, 张锐.岩溶区桩基冲切破坏模式及安全厚度研究[J]. 岩土力学, 2012, 33(2): 524−530.ZHAO Minghua, LEI Yong, ZHANG Rui. Study of punching failure mode and safe thickness of pile foundation in karst region[J]. Rock and Soil Mechanics, 2012, 33(2): 524−530.
[7] 张惠乐, 张智浩, 王述红, 等. 岩溶区嵌岩桩的试验研究与分析[J]. 土木工程学报, 2013, 46(1): 92−103. ZHANG Huile, ZHANG Zhihao, WANG Shuhong, et al. Experimental study and analysis on rock-socketed pile in karst area[J]. China Civil Engineering Journal, 2013, 46(1): 92−103.
[8] 黄生根, 梅世龙. 南盘江特大桥岩溶桩基承载特性的试验研究[J]. 岩石力学与工程学报, 2004, 23(5): 809− 813. HUANG Shenggen, MEI Shilong. Testing study on bearing behavior of piles for Nanpan River great bridge in karst area[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 809−813.
[9] 刘善军, 宋长斌. 隐伏碳酸盐岩区第四系松散盖层稳定性分析[J]. 中国地质灾害与防治学报, 2003, 14(1): 18−21.LIU Shanjun, SONG Changbin. Stability analysis of Quaternary loose cover in carbonate rock region[J]. The Chinese Journal of Geological Hazard and Control, 2003, 14(1): 18−21.
[10] 曾中林, 曾大艇, 李韬宇, 等. 岩溶区条形刚性基础下伏孔洞顶板冲切极限承载力变分分析[J]. 自然灾害学报, 2018, 27(5): 27−38.ZENG Zhonglin, ZENG Dating, LI Taoyu, et al. Variation analysis of ultimate bearing punching capacity of roof underlying the rigid strip foundation in karst area[J]. Journal of Natural Disasters, 2018, 27(5): 27−38.
[11] 雷勇, 陈秋南, 马缤辉.基于极限分析的桩端岩层冲切分析[J]. 岩石力学与工程学报, 2014, 33(3): 631−638.LEI Yong, CHEN Qiunan, MA Binhui. Punching analysis of rock at pile tip base on limit analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(3): 631−638.
[12] Maksimovic M. Nonlinear failure envelope for soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1989, 115(4): 581−586.
[13] Baker R. Nonlinear Mohr envelopes based on triaxial data[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2004, 130(5): 498−506.
[14] Hoek E, Brown E T. Practical estimate the rock mass strength[J]. International Journal of Rock Mechanics and Mining Science, 1997, 34(8): 1165−1186.
[15] YANG X L, YIN J H. Slope stability analysis with nonlinear failure criterion[J]. Journal of Engineering Mechanics, ASCE, 2004, 130(3): 267−273.
[16] ZHAO L H, LI L, YANG F, et al. Upper bound analysis of slope stability with nonlinear failure criterion based on strength reduction technique[J]. Journal of Central South University of Technology, 2010, 17(4): 836−844.
[17] ZHAO Lianheng, YANG Feng, ZHANG Yingbin, et al. Effects of shear strength reduction strategies on safety factor of homogeneous slope based on a general nonlinear failure criterion[J]. Computers & Geotechnics, 2015, 63: 215−228.
[18] 谭亦高, 左仕, 胡世红, 等. 三维圆形浅埋锚板极限抗拔力非线性上限解析[J]. 铁道科学与工程学报, 2017, 14(6): 1166−1173.TAN Yigao, ZUO Shi, HU Shihong, et al. Study on the ultimate pullout capacity of 3-D shallow circle plate anchors[J]. Journal of Railway Science and Engineering, 2017, 14(6): 1166−1173.
[19] 张佳华, 张标. 非线性屈服准则下浅埋隧道支护参数上限解[J]. 铁道科学与工程学报, 2018, 15(8): 2061− 2071.ZHANG Jiahua, ZHANG Biao. Upper bound solutions of support parameter for shallow tunnels in nonlinear soil masses[J]. Journal of Railway Science and Engineering, 2018, 15(8): 2061−2071.
Punching analysis of soil under circular foundation based on nonlinear M-C criterion
WANG Zhibin, LUO Xiexin, XIA Haoxiang
(School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)
The nonlinear Mohr-Coulomb failure criterion and the associated flow rule have been introduced according to the characteristics of soil mass, and then the punching failure mechanism of the soil with an underlying circular rigid foundation was constructed. Then the calculation formula of the ultimate bearing capacity was established using limit analysis method. Furthermore, the ultimate bearing capacity of the soil with an underlying circular rigid foundation was obtained in the condition of arbitrary combination of parameters. The Plaxis 3D software was used to analyze, and the numerical results were in agreement with the theoretical solutions, which verified the validity of the proposed method. The influence of parameters on ultimate bearing capacity was also analyzed, and the results shows that the influence of the nonlinear coefficienton the ultimate bearing capacity is obvious, and that the ultimate bearing capacity decreases with the increase of, and the decreasing trend tends to be gentle with given parameters,. The ultimate bearing capacity increases with the0of initial cohesive force of soil, the roof thickness and the rigidity foundation width, and decreases with the increase of soil weight and the increase of soil tensile strength.
nonlinear Mohr-Coulomb failure criterion; limit analysis; ultimate bearing capacity; circular foundation; punching
10.19713/j.cnki.43−1423/u.2019.03.011
TU473
A
1672 − 7029(2019)03 − 0637 − 09
2018−04−01
国家重点研发计划资助项目(2017YFB1201204)
王志斌(1975−),男,湖南桃江人,讲师,博士,从事边坡稳定性及隧道围岩稳定性等研究;E−mail:71496933@qq.com
(编辑 涂鹏)
