动车组辅助供电系统健康状态评估
2019-04-16赵峰李渊琴高锋阳陈鲜
赵峰,李渊琴,高锋阳,陈鲜
动车组辅助供电系统健康状态评估
赵峰1, 2,李渊琴1,高锋阳1,陈鲜1
(1. 兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070; 2. 兰州交通大学 光电技术与智能控制教育部重点实验室,甘肃 兰州 730070)
以CRH3型动车组辅助供电系统为例,采用一种基于合作博弈和云模型理论的健康状态评估方法,建立辅助供电系统健康状态评估指标体系,获取各元件指标及元件层的组合权重,确定各元件指标对动车组辅助供电系统各状态等级的隶属度,采用分层评估方法得到评估结果。研究结果表明:本文所采用的方法能够结合辅助供电系统的分层分析模型,直观地给出各指标、各元件以及辅助供电系统整体的健康状态信息,有效完成CRH3型动车组辅助供电系统的健康状态评估。
动车组;辅助供电系统;合作博弈;云模型;健康状态评估
定期检修是目前最常用的检修方式,然而,当设备处于健康状态时,这种检修方式会造成检修过度。近年来,为了提高检修效率,一种新的检修方式——状态检修,被应用在设备或复杂系统的检修中。目前,健康状态评估在许多领域中都有研究,路广勋等[1]将云重心法运用在液压泵的健康状态评估中,验证了该方法的可行性;齐继阳等[2]运用熵权法和可拓层次分析法计算各关键部件和相关指标的权重,运用灰色聚类法和模糊综合评判法分别对液压系统关键部件和整个液压系统进行健康状态评估;雷从英等[3]将云模型运用在齿轮的健康状态评估中,并结合案例证明了该方法的有效性。运用在健康状态评估中的方法主要有层次分析法、熵权法和模糊综合评判法等方法,但传统的单一方法在评估过程中存在一定的问题,郑彦涛等[4−5]在确定权重时采用层次分析法,但其主观性较强,得到的权重精确度不高;Shannon[6]采用熵权法确定权重,熵权法确定权重时,对指标差异程度不大的评估问题,得到的权重准确度不高,具有一定局限性;王玘等[7]在评估航空发动机的健康状态时,采用模糊综合评判法确定航空发动机各指标对各状态等级的隶属度,但模糊综合评判法在确定隶属度时准确度不高。针对以上各单一方法的不足,本文以CRH3型动车组辅助供电系统作为分析实例,基于合作博弈法和云模型理论对动车组辅助供电系统进行健康状态评估,采用将客观方法熵权法和灰关联度法、主观方法层次分析法相结合的合作博弈法,可以得到精确度较高的组合权重,采用云模型理论确定各指标对动车组辅助供电系统运行状态的隶属度,使最终的评估结果更加科学合理。
1 辅助供电系统健康状态评估方法
1.1 确定权重方法
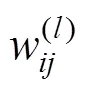
1.1.1 熵权法
熵权法是一种确定权重的客观方法[6],其主要步骤如下。

步骤2:确定信息熵。系统中第个元件第个指标的信息熵定义为:
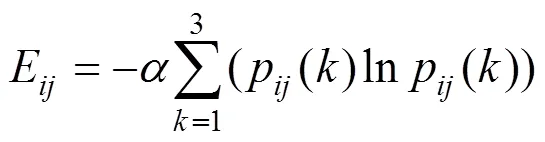
式中:=1/ln。
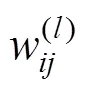
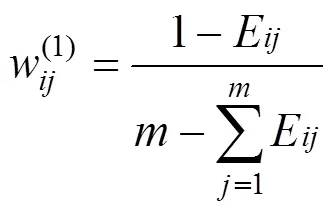
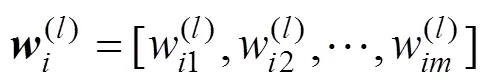
1.1.2 层次分析法
层次分析法是一种在确定权重方面应用很广泛的方法[4]。其主要步骤如下。
步骤1:将复杂系统采用分层分析模型分解成由关键部件和指标组成的递阶层次结构图。
步骤2:根据指标间的隶属关系,进行两两比较,构造出判断矩阵,采用T. L. Sataty1-9标度法表示不同指标两两比较的结果,如表1所示。

表1 T. L. Sataty1~9比例标度法取值及含义
步骤3:利用公式CR=CI/RI对进行一致性检验,其中:CR为的随机一致性比率;CI为的一致性指标,由CI=(max−)/(−1)计算得出;RI为的平均随机一致性指标[7],用以消除矩阵阶数的影响,RI的取值如表2所示。一般,≥3时,当0 表2 1~10阶成对比较矩阵RI的取值 1.1.3 灰关联度法 灰色关联法的主要步骤如下。 步骤2:计算关联度。X()对X()(≠)的关联度系数为: 式中:为分辨系数,其取值一般为0.5[8]。 X()对X()(≠)的关联度为: 步骤3:权重计算。依据步骤2,计算第行两两元素间的关联度,构成关联度矩阵,即 1.1.4 合作博弈法 则对于系统中某个元件基于合作博弈法的权重向量为=[w1,w2, …,w]。 云模型可以实现定性概念与定量数值之间的转换,C(,,e)为云参数[1]。图1为=0.5,=0.166 7,e=0.015的正态云分布图,其中为期望,代表该论域中最典型的样本点;为熵,代表定性概念的模糊度;e为超熵,即熵的熵,反映该论域中所有点的凝聚性,即云滴的厚度[10]。 图1 Ex=0.5,En=0.166 7,He=0.015的正态云分布图 影响动车组辅助供电系统健康状态的因素较多,而动车组辅助供电系统是一个复杂、庞大的系统,其各因素的影响程度不同,各因素之间又存在联系,在进行动车组辅助供电系统健康状态评估时,很难考虑到影响其健康状态的所有因素,因此,本文只选取具有代表性的评估状态量,将整个系统分为系统层、元件层和指标层等3个层次构成,如图2所示。 本文将辅助供电系统的实际健康状态划分为5个等级,具体如下:T={T1,T2,T3,T4,T5}={好,较好,一般,较差,差}。 好:各指标检测值处于最优值附近,系统能安全运行。此时,系统不需要检修,可以延长检修 计划。 较好:个别指标检测值略有下降,但系统无劣化趋势,仍能正常运行。此时,系统可按计划进行检修。 一般:某些指标检测值下降幅度较大,但系统仍能正常运行。此时,可对系统计划安排优先检修。 较差:某些指标检测值下降幅度较大,系统运行状态欠佳,容易发生故障,劣化趋势较明显。此时,应尽快安排系统检修。 差:某些指标检测值严重偏离设计值,系统整体状态欠佳,已无法正常运行,性能劣化趋势非常明显。此时,需立即进行相关处理。 图2 动车组辅助供电系统分层分析模型 以CRH3型动车组辅助供电系统为例进行分析。对于辅助变流器,其指标分别为输入电压(C1)、总谐波失真(C2)、三相负载允许不平衡度(C3)和效率(C4);对于充电机,其指标分别为输入电压(C5)、输入频率(C6)和输出功率(C7);对于蓄电池,其指标分别为容量(C8)、输出电压(C9)和允许环境温度(C10)。 根据文献[13−14]中确定阈值的方法及现场评估经验,辅助变流器、充电机、蓄电池的健康状态评估指标的阈值如表3所示。 某CRH3型动车组辅助供电系统各元件指标在某3个时间段检测到3组相关数据的平均值如表4所示。 表3 辅助供电系统各元件健康状态评估指标阈值 表4 某CRH3型动车组辅助供电系统各元件指标检测数据 由于能反应动车组辅助供电系统健康状态的指标标度类型和量纲都不相同,为将量纲数据变为无量纲数据,需利用规范化公式将原始数据进行处理,将其压缩在[0,1]之间。由于动车组辅助供电系统各元件的指标都为定量指标,故其规范化公 式为: 式中:x()′为第个元件第个指标的第个检测值;x为该指标的极限值,即最差值;x为该指标的最优值;x()为第个元件第个指标的第个检测值的规范化值;原始数据利用式(10)规范化处理后的数据如表5所示。 3.2.1 熵权法确定元件指标权重 表5 辅助供电系统各元件的指标规范化数据 3.2.2 层次分析法确定元件指标权重 以元件层元件之一的辅助变流器为例,通过专家经验给定辅助变流器各指标两两比较时的重要性标度,写成判断矩阵形式,即: 3.2.3 灰关联度法确定权重 按上述步骤,依次求得辅助变流器指标两两间的关联度得关联矩阵1。 表6 辅助变流器指标的绝对差数列 表7 辅助变流器指标的关联度系数 表8 辅助变流器指标的关联度 3.2.4 合作博弈法确定元件指标组合权重 同样,计算得元件层其他元件,即充电机、蓄电池的组合权重向量分别为2=[0.295 1,0.337 1,0.367 8],3=[0.338 8,0.231 5,0.429 8]。 图3为3种计算权重的方法和合作博弈法计算的指标层权重结果,由图3可以看出,合作博弈法下求得的指标权重介于3种单一方法求得的指标权重之间,避免单一确定权重的方法导致权重精确度变差。 图3 辅助供电系统指标层权重值 辅助供电系统各元件的模糊隶属度函数以及云模型函数如表9所示,根据辅助供电系统各元件的云模型参数可以得到其对应的定性评测云发生器,如图4所示。 图4 辅助供电系统各元件的正态云分布图 表9 辅助供电系统各元件的模糊隶属度函数以及云模型参数 因此,辅助变流器各指标对5个等级的隶属度构成了评判矩阵: 用同样的方法得到元件层其他元件,即充电机、蓄电池各指标对5个等级的隶属度构成的评判矩阵分别为: 综合以上结果,求得辅助供电系统的评判矩阵为: 根据最大隶属度法,取与max=max [b|=1, 2,…,5]相对应的评判集元素作为评估结果,从而判断出辅助供电系统的健康状态等级。根据已计算的辅助供电系统的评估向量=·=[0.604 8,0.273 7,0.043 2,0.001,0],再根据最大隶属度法,即max=max[b|0.604 8,0.273 7,0.043 2,0.001,0],则可得max=0.604 8,在评估向量中,0.604 8所对应的状态等级为好,所以可得辅助供电系统的健康状态等级是好,根据评估结果可知该动车组辅助供电系统能正常运行。 1) 以CRH3型动车组辅助供电系统为具体研究对象,验证了合作博弈法和云模型理论评估方法的有效性。 2) 采用合作博弈法计算辅助供电系统元件层及各元件指标权重,可弥补3种单一确定权重方法的不足,得到准确率更高的权重。 3) 研究结果表明,本文所采用的健康状态综合评估方法运用在CRH3型动车组辅助供电系统的健康状态评估中,能得到准确的评估结果。 [1] 路广勋, 李建增, 李鹏俊. 基于云重心法的发射场液压泵的健康状态评估[J]. 计算机测量与控制, 2014, 22(3): 800−802. LU Guangxun, LI Jianzeng, LI Pengjun. State assessment of the hydraulic pump of launch site based on cloud gravity evaluation[J]. Computer Measurement & Control, 2014, 22(3): 800−802. [2] 齐继阳, 王凌云, 李金燕, 等. 液压系统健康状态的综合评估方法[J]. 机械设计与制造, 2016(5): 56−60. QI Jiyang, WANG Lingyun, LI Jinyan, et al. Method of comprehensive health assessment of the hydraulic system[J]. Machinery Design & Manufacture, 2016(5): 56−60. [3] 雷从英, 夏良华, 郝晋峰. 云模型在齿轮健康状态评估中的应用研究[J]. 机械传动, 2013(12): 22−26. LEI Congying, XIA Lianghua, HAO Jinfeng. Research on the application of cloud model in gear health condition assessment[J]. Journal of Mechanical Transmission, 2013(12): 22−26. [4] 郑彦涛. 基于层次分析法的CRH380B动车组维修可靠性分析与研究[D]. 北京: 清华大学, 2013. ZHENG Yantao. Hierarchy analysis based maintenance reliability for CRH380B series electric motor units[D]. Beijing: Tsinghua University, 2013. [5] Mordeson J N, Wierman M J, Clark T D, et al. The analytic hierarchy process[M]. Encyclopedia of Biostatistics, John Wiley & Sons, Ltd, 2013: 19−28. [6] Shannon C E. A mathematical theory of communication [J]. Bell System Technical Journal, 2014, 27(3): 379−423. [7] 王玘, 何正友, 程宏波, 等. 基于多层免疫原理与模糊统计的地铁牵引供电系统健康评估方法[J]. 铁道学报, 2015(12): 31−39. WANG Qi, HE Zhengyou, CHENG Hongbo, et al. Health assessment method for metro traction power supply system based on multi-layer immune principle and fuzzy statistics[J]. Journal of the China Railway Society, Railway Engineering, 2015(12): 31−39. [8] 游桂芝, 鲍大忠. 灰色关联度法在地质灾害危险性评价指标筛选及指标权重确定中的应用[J]. 贵州工业大学学报(自然科学版), 2008, 37(6): 4−8. YOU Guizhi, BAO Dazhong. Gray correlative degree in geological hazard evaluation and election index weights to determine the application[J]. Journal of Guizhou University of Technology (Natural Science Edition), 2008, 37(6): 4−8. [9] Purba J H. A fuzzy-based reliability approach to evaluate basic events of fault tree analysis for nuclear power plant probabilistic safety assessment[J]. Annals of Nuclear Energy, 2014(70): 21−29. [10] ZHENG R, MA Z, WU Q, et al. Numerical characteristics analysis of cloud model and its application to random IOT security risk assessment[J]. International Journal of Applied Mathematics & Statistics, 2013, 48(18): 143− 153. [11] 郑建辉, 王天辉, 张超恒. 基于云重心评判法的装备维修保障效能评估[J]. 舰船电子工程, 2016, 36(3): 115− 117, 129. ZHENG Jianhui, WANG Tianhui, ZHANG Chaoheng. Efficiency evaluation of equipment ervice base on cloud gravity center assessment method[J]. Ship Electronic Engineering, 2016, 36(3): 115−117, 129. [12] 王开铭. 高速铁路牵引变电所可靠性分析与风险评估[D]. 兰州: 兰州交通大学, 2017. WANG Kaiming. Reliability analysis and risk assessment of high-speed railway traction substation[D]. Lanzhou: Lanzhou Jiaotong University, 2017. [13] 刘民. 动车组辅助供电系统研究[D]. 成都: 西南交通大学, 2016. LIU Min. The research of EMU auxiliary power supply system[D]. Chengdu: Southwest Jiaotong University, 2016. [14] 何正友. 复杂系统可靠性分析在轨道交通供电系统中的应用[M]. 北京: 科学出版社, 2015: 224−242. HE Zhengyou. Complex system reliability analysis and application in rail transit power supply system[M]. Beijing: Science Press, 2015: 224−242. Health assessment of EMU auxiliary power supply system ZHAO Feng1, 2, LI Yuanqin1, GAO Fengyang1, CHEN Xian1 (1. School of Automation and Electrical, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. Key Laboratory of Opto-Technology and Intelligent Control Ministry of Education, Lanzhou Jiaotong University, Lanzhou 730070, China) A method based on cooperative game method and cloud model was adopted to evaluate the health status with auxiliary power supply system of CRH3 EMU as an example in this paper. An evaluation index system of auxiliary power supply system health status assessment was established, the cooperative game method was adopted to obtain the combination weights of each component’s index and component layer. Cloud model was applied to obtain the membership degree of each component’s index to each auxiliary power supply system status grade. Hierarchical evaluation was used to assess auxiliary power supply system status. The results show that the adopted method combines the layered analysis model of auxiliary power supply system, and intuitive information on the health status of each index, key components and auxiliary power supply system can be gotten, meanwhile, the health status assessment of CRH3 EMU auxiliary power supply system can also be carried out effectively. EMU; auxiliary power supply; cooperative game; cloud model; health status assessment 10.19713/j.cnki.43−1423/u.2019.03.004 U266 A 1672 − 7029(2019)03 − 0581 − 09 2018−04−02 国家重点研发计划资助项目(2017YFB1201003-020);光电技术与智能控制教育部重点实验室开放课题资助项目(KFKT2016-6) 赵峰(1966−),男,上海人,教授,从事铁道电气化与自动化、电能质量分析及控制方面的研究;E−mail:zhaofeng818@163.com (编辑 涂鹏)
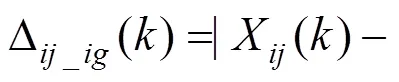
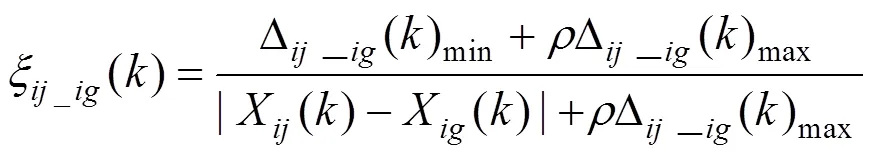
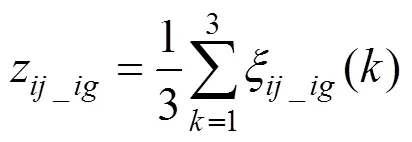



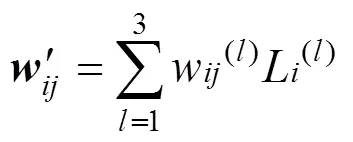
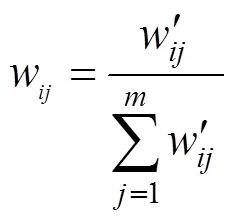
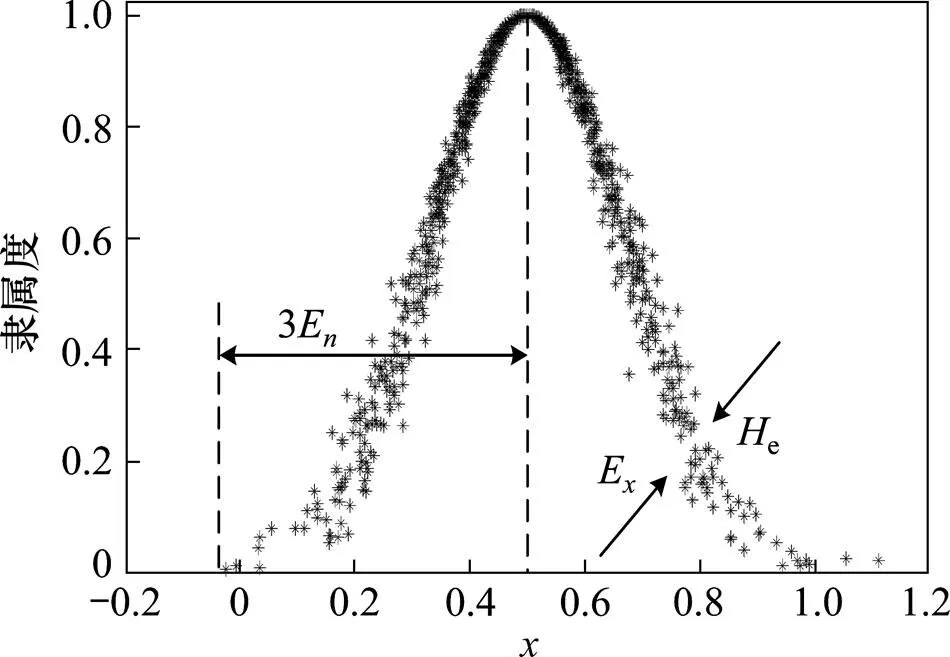
1.2 云模型理论

2 辅助供电系统分层分析模型的建立
2.1 辅助供电系统健康状态等级的划分

2.2 辅助供电系统各元件指标参数
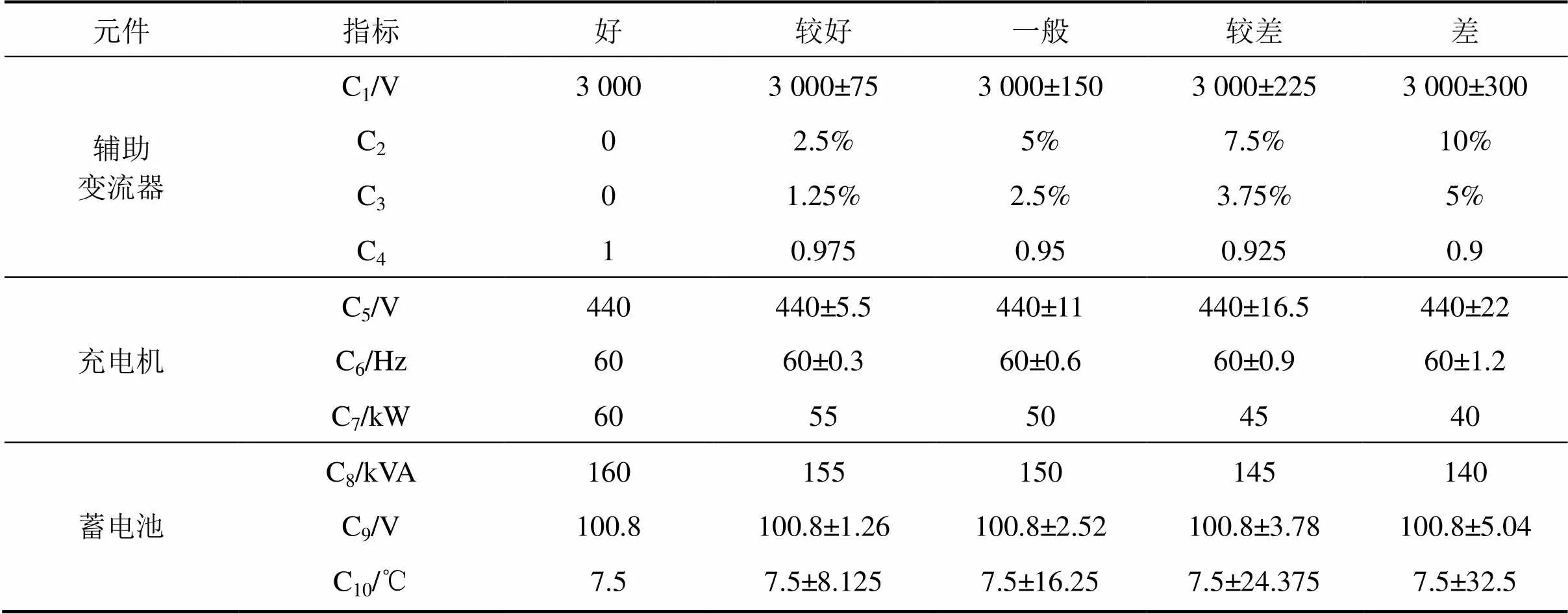
3 CRH3型动车组辅助供电系统健康状态评估实例分析
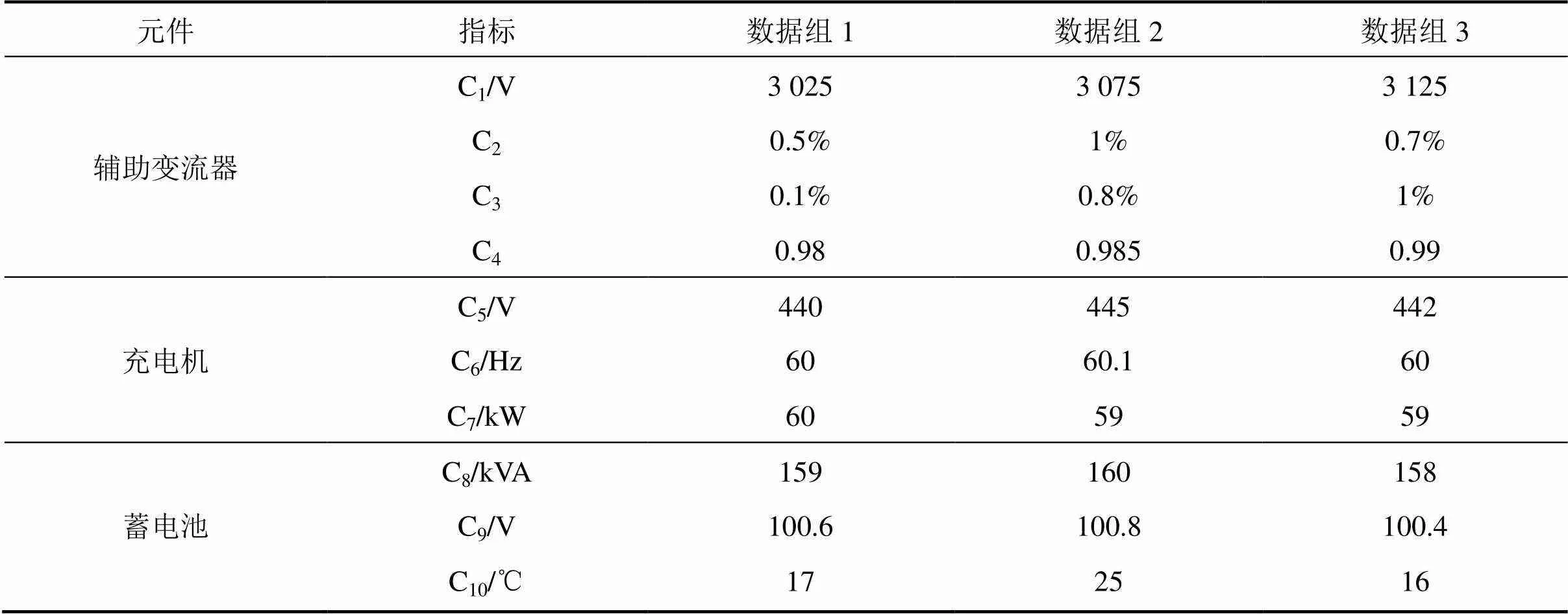
3.1 原始数据处理
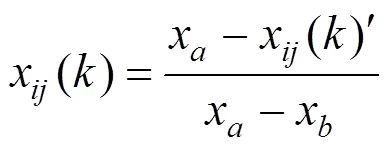
3.2 权重确定

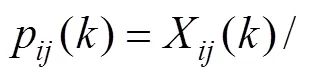
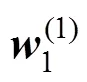





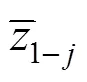



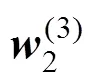

3.3 辅助供电系统各元件隶属度的确定
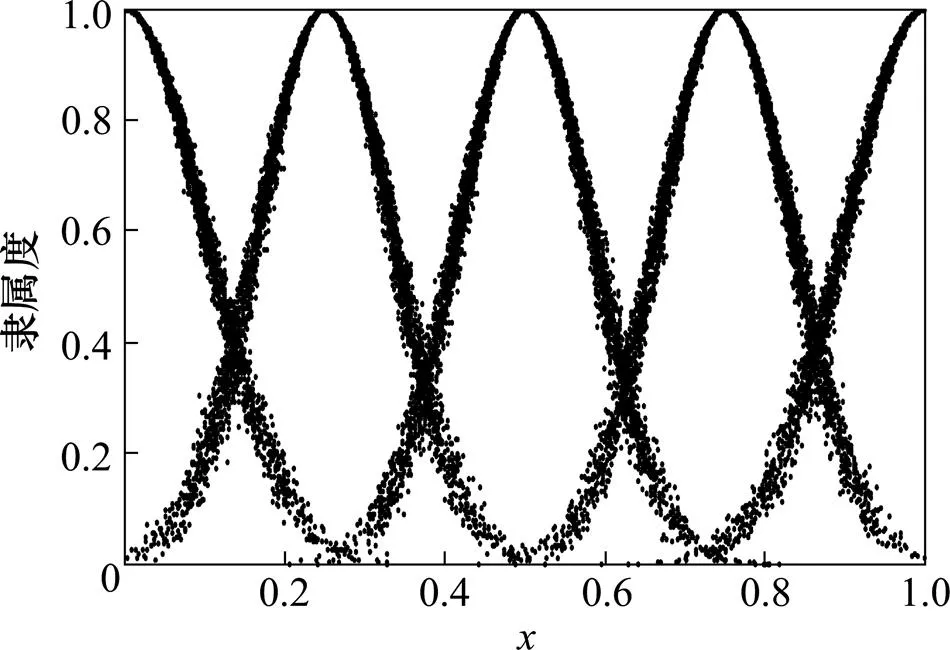


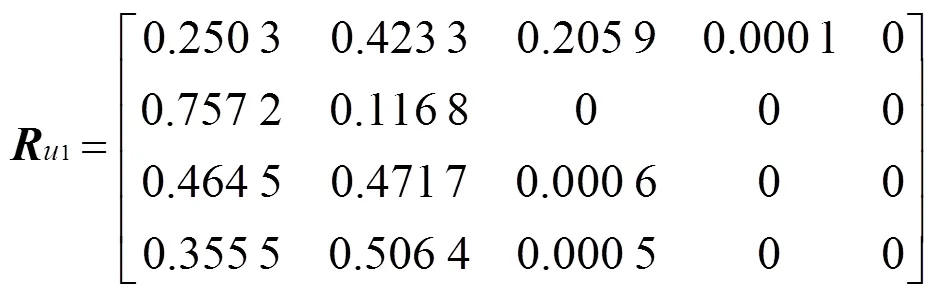

3.4 辅助供电系统健康状态综合评估
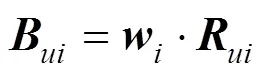

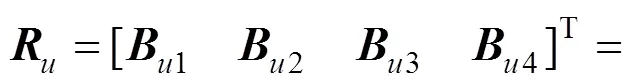
4 结论
