基于简化数值模型的高墩桥梁减隔震性能研究

2019-04-16马振霄贾少敏

中外公路 2019年4期

马振霄，贾少敏

(广州大学工程抗震研究中心，广东广州 510405)

丘陵山区由于地形地质条件复杂，桥梁结构占比大且高墩桥梁日益增多。高墩的长细比和墩身自重通常都比较大，90 m桥墩墩身自重与上部结构自重之比可达2.38。高墩桥梁的结构特点使其与常规桥梁的抗震性能存在较大不同。在地震作用下，高墩震害多表现为墩梁相对位移过大导致的支座移位、活动支座脱落，上部结构位移过大导致的墩台破坏以及墩身的弯矩破坏，其中又以墩身弯矩所造成的破坏最为严重，因此高墩桥梁的抗震性能研究越来越受到设计人员和学者的重视。

高墩桥梁抗震性能研究主要集中在3个方面：① 增加结构自身的强度和变形能力以抗震；② 选择适当的塑性铰位置进行延性设计；③ 引入附加装置进行减隔震设计。相比前两种方法，减隔震措施主要通过特定构件消耗体系中的能量或改变体系的动力特性以减弱结构地震响应，一定程度降低抗震方案设计验算的困难和延性设计方案震后修复的代价。文献[9]主要讨论了高墩桥梁中使用滑动支座、黏滞阻尼器等减隔震装置的必要性；文献[10]通过对采用铅芯橡胶支座、盆式橡胶支座和双曲面滑动支座高墩桥梁的减隔震性能分析表明，减隔震支座具有一定控制震动效果，但与墩高和频谱特性紧密相关，抗震设计中应根据具体情况谨慎分析。

为进一步分析强震区高墩桥梁减隔震装置的适用性及其控制效果，该文结合高墩桥梁基本周期长的特点，着重考虑附加装置的耗能能力，提出摩擦摆支座(FPI)与黏滞阻尼器(FVD)的组合减隔震方案，并进行该组合装置的参数分析和地震动幅值、频谱影响分析。

1 研究方法

文献[6]认为规则梁桥可简化为等效单自由度模型进行抗震设计。对于高墩桥梁而言，墩身质量一般大于上部结构质量，在地震作用下墩身振型和几何非线性贡献必然加大，此时仍采用等效单自由度模型则可能过于简化，不能完全反映高墩桥梁的地震响应。文献[8]均采用单质点悬臂梁(MSC)模型，考虑墩身材料和几何非线性对地震响应的影响，使计算结果更趋合理。该文参考MSC的简化思路建立有限元模型，见图1。

1.1 单质点悬臂梁有限元模型

桥墩采用空间梁单元(Ansys17.0中Beam188单元，网分1 m)模拟，上部结构质量堆积在支座顶点并用集中质量单元(Mass21)模拟，平动质量实常数通过文献[4]提供的质量比确定，考虑绕横轴(图1所示y轴)转动质量的影响。计算模型分别以20、90 m作为低墩和高墩桥梁的代表。两种模型的具体设计参数见表1。

图1 桥梁简化模型

表1 两种模型有限元参数设计表

为达到利用附加装置耗散体系内地震能量的目的，选用以摩擦耗能为主的支座FPI和以黏滞耗能为主的装置FVD。FPI双线性滞回模型如图2所示。

图2 FPI双线性滞回模型

FPI参数参考文献[13]，其中：

(1)

式中：K1和K2分别为屈服前、后刚度；Fy和dy分别为屈服力和屈服位移；μ为摩擦系数(取动静摩擦系数相等)；W为上部结构静重；R为支座半径。

FVD是一种速度型阻尼器，力学模型如下：

F=C|v|nsgn(v)

(2)

式中：F为阻尼力；C为阻尼系数；v为关注点间相对速度；n为速度指数。

研究仅考虑纵桥向地震响应。减隔震装置安装在墩顶和主梁间(即简化模型质点与墩顶之间)。FPI和FVD分别通过非线性弹簧单元Combin40和Combin37模拟。Combin40单元由相互平行的弹簧滑动器和阻尼器组合而成，每一个节点有一个自由度。利用该单元模拟FPI时释放纵桥向自由度，并赋予相应的刚度K1、K2和阻尼系数C。值得注意的是，该单元工作弹性阶段的刚度为K1与K2之和，进入塑性阶段后K1变为0，K2参与工作。K1、K2可根据滞回曲线简单计算得到，C可通过式(3)确定。Combin37单元是具有打开和关闭性能的单向单元，每个节点只有一个自由度。通过适当的参数调节该单元可以模拟黏滞阻尼器。需要的速度可通过控制节点计算得到，该文算例中控制节点为墩梁连接处对应节点。支座竖向通过大刚度法模拟，其转动方向与墩梁对应节点主从约束。参考抗震模型的墩梁连接以固结简化。

体系采用前两阶模态频率确定的Rayleigh阻尼，振型阻尼比为0.05。

(3)

式中：ζeq和Keq分别为等效阻尼比和等效刚度；g为重力加速度，取9.8 m/s2。

1.2 有限元模型精度控制

利用Ansys17.0进行瞬态动力分析时，系统矩阵处理采用完全矩阵法(Full Method)：避免因振型参与程度不同和质量近似产生的误差；方便同时考虑材料和几何非线性。梁单元形函数采用3阶多项式。动力控制方程求解采用Newmark-β法，激活自动计算积分步长选项(AUTOS，ON)。高墩模型在地震作用下的二阶效应不容忽视，激活大变形效应(NLGEOM，ON)。

利用文中研究方法进行非线性时程分析时隐含以下假设：① 墩梁为弹性构件；② 上部结构纵桥向刚度无穷大；③ 被简化桥梁的形制规整且墩高一致；④ 硬土场地条件下土结方式按固结简化。

2 减隔震分析

激励选择EL Centro波，假定峰值加速度为3.124 m/s2，持时31.2 s。在模型纵桥向直接输入该加速度进行时程分析。

2.1 摩擦摆支座

摩擦摆支座(FPI)的本构关系如图2所示。初始支座参数参考文献[13]确定，其中支座初始刚度取dy为2.5 mm时的刚度，减隔震位移量D取100 mm。FPI半径和摩擦系数分别取工程中常见的范围：0.5～2.5 m(以0.5 m为一阶)和0.01～0.09(以0.02为一阶)。

对20、90 m简化模型分别进行纵桥向FPI的减隔震分析，结果如图3、4所示。

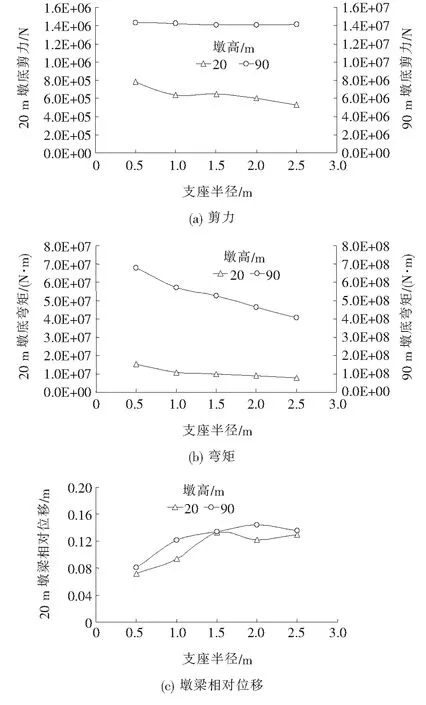
图3 两种模型采用FPI时力学性能随支座半径变化图(摩擦系数0.01)

图4 两种模型采用FPI时力学性能随支座摩擦系数变化图(支座半径2 m)

从图3、4可以看出：采用FPI的两种模型随支座半径的增大，剪力、弯矩存在一定差异：20 m模型单调递减而90 m模型先减小后增大；墩梁相对位移变化相对一致。两种模型随支座摩擦系数的增大变化规律整体相似：剪力、弯矩先减小后增大，墩梁相对位移单调递减。内力与变形存在竞争关系。

2.2 黏滞阻尼器

对20、90 m简化高墩桥梁模型纵桥向采用黏滞阻尼器FVD进行减震分析。20 m模型阻尼系数n分别取1、10、100、1 000和2 000 kN/(m·s-1)n，90 m桥梁分别取200、2 000、4 000、8 000和10 000 kN/(m·s-1)n；速度指数分别取0.25、0.3、0.5、0.7和0.9。

图5、6为20、90 m模型分别采用FVD时力学性能随阻尼系数变化图，图7为两种模型采用FVD时力学性能随速度指数变化图。从图5、6可以看出：采用FVD时随阻尼系数的增大，剪力、弯矩先减小后增大，墩梁相对位移递减；90 m模型随阻尼系数的变化影响更大。从图7可以看出：随速度指数的增大，墩梁相对位移先减小后增大。同样地，内力与变形存在竞争关系。

2.3 摩擦摆支座与黏滞阻尼器组合方案

定义减震率(负数表示减震)：

(4)

根据式(4)计算得到20、99 m桥梁简化模型的减震率见表2。

图5 20 m模型采用FVD时力学性能随阻尼系数变化图

图6 90 m模型采用FVD时力学性能随阻尼系数变化图

从表2可以看出：90 m模型的减隔震控制效率明显低于20 m，与理论判断一致，但墩梁相对位移有所降低。如何有效提升减隔震装置对内力的控制是高墩桥梁减隔震设计的重点之一。为进一步提高高墩桥梁的减隔震效果，该文侧重考虑附加装置的耗能能力，设计了FPI+FVD的组合方案。以下重点研究这种组合方案。

为研究该文提出的FPI+FVD组合减隔震方案的可行性，设计以下研究方法：首先取FVD速度指数为常量0.5，以FVD阻尼系数、FPI支座半径和摩擦系数为变量，分析53=125种工况下响应；在以上优化参数的基础上分析当速度指数分别为0.1、0.3、0.7和0.9时响应的变化趋势。具体计算结果见图8～13(限于篇幅只给出部分图示)。

从图8～10可知：组合工况中FPI支座半径对剪力的影响不甚敏感，阻尼系数较小时支座半径对弯矩的影响较大；随FVD阻尼系数C的增大，摩擦系数对剪力、弯矩的影响趋势由先减小后增大变为单调递增(绝对值逐渐增大)；墩梁相对位移则随支座半径的增加单调递减，与剪力、弯矩形成竞争关系。图11～13亦有类似规律。总的来看，在速度指数为0.5时组合参数存在一定范围的优解。综合考虑内力和位移的减震效果，选择FPI摩擦系数μ=0.03、支座半径R=1 m、FVD阻尼系数C=2 000 kN/(m·s-1)n进行速度指数n的确定(图14)。

图7 两种模型采用FVD时力学性能随速度指数变化图

表2 FPI和FVD减震率统计

从图14可以看出：在其他参数一定的情况下，剪力、弯矩随FVD速度指数的增加先减小后增大，墩梁相对位移则单调递增。整体来看：相对位移得到了有效控制，速度指数为0.7时内力取得极小值；此时剪力、弯矩、墩顶位移和桥面位移的减震率分别为-20.72%、-35.57%、-36.05%和-11.73%。

基于通信的列车控制(communication based train control,CBTC)系统是轨道交通的主流技术[1],目前CBTC开始使用工作在1.8 GHz的LTE-M(long term evolution-metro)技术.多输入多输出(multiple-input multiple-output,MIMO)作为LTE-M的关键技术,在不增加带宽的情况下能有效提升系统容量.因此,研究隧道环境下MIMO无线信道特性对于系统设计和优化至关重要.

图8 90 m模型采用组合装置时墩底剪力随摩擦系数变化图(速度指数0.5)

图9 90 m模型采用组合装置时墩底弯矩随摩擦系数变化图(速度指数0.5)

图10 90 m模型采用组合装置时墩梁相对位移随摩擦系数变化图(速度指数0.5)

图11 90 m模型采用组合装置时墩底剪力随阻尼系数变化图(速度指数0.5)

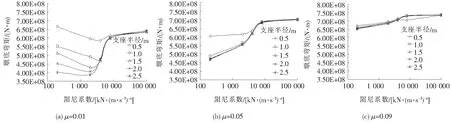
图12 90 m模型采用组合装置时墩底弯矩随阻尼系数变化图(速度指数0.5)

图13 90 m模型采用组合装置时墩梁相对位移随阻尼系数变化图(速度指数0.5)

图14 90 m模型采用组合装置时响应随速度指数变化图

表3为FPI、FVD和FPI+FVD等3种减隔震方案的减震效果对比情况。从表3可看出：除剪力外组合方案在该模型中的优势并不明显。整体而言，FVD方案可能更具竞争性。

表3 3种减隔震方案的减震效果对比表

2.4 地震动幅值和频谱分析

以上节优化后模型为研究对象，另选取具有代表性的KERN波、NORTHR波、DUZCE波和KOBE波进行频谱分析(PGA均调为EL Centro的3.124 m/s2)，一定程度上体现地震动的随机性；以EL Centro原波为底波试算当PGA分别为0.8、0.6、0.4和0.2倍时90 m桥梁模型的地震响应。所选用地震动特性见表4。表5为EL Centro波幅值对90 m桥梁模型响应的影响，表6为不同地震动对90 m模型响应的影响。

表4 选用地震动特性

续表4

选用波地震事件、测站、方向及记录时间PGV/PGA/s卓越周期/tNORTHR_SCS052Northridge-01Sylmar - Converter Sta52, 1/17/19940.1900.75DUZCE_SKR090Duzce TurkeySakarya90, 11/12/19990.2140.10KOBE_KJM000Kobe JapanKJMA0, 1/16/19950.1110.20

从表5可以看出：随地震动幅值的减弱，各响应绝对值降低的同时减震率也下降。幅值对该模型地震响应的影响明显，强震区高墩桥梁采用该文提出的组合方案减隔震效果尚可。

从表6可以看出：不同地震动频谱特性对模型地震响应影响明显，剪力、弯矩、墩顶位移和桥面位移的平均减震率分别为4.19%、-12.53%、-21.19%、4.70%，墩梁相对位移为66 mm。该模型的鲁棒性仍有待提高。