预应力连续钢梁负弯矩区受力性能分析

2019-04-16王宇琪贾艳敏魏皓天王佳伟

中外公路 2019年4期

王宇琪，贾艳敏*，魏皓天，王佳伟,2

(1.东北林业大学土木工程学院，黑龙江哈尔滨 150040； 2.辽宁省交通规划设计院有限责任公司公路养护技术研究中心)

1 前言

在桥梁工程中，预应力钢梁相较于普通钢梁，其承载能力大幅提高，结构整体受力性能有很大改善，连续钢梁不同于简支钢梁，支座截面出现较大负弯矩，对跨中正弯矩有明显卸载作用，故连续钢梁在大跨径桥梁中得以广泛应用。目前对钢梁受力性能分析多为简支钢梁，桑敏对体外预应力简支工字钢梁进行参数分析，包括转向块数量、体外张拉偏心、布索形式等对抗弯性能的影响；段兰分析了混合设计高性能简支工字钢梁翼缘宽厚比、腹板高厚比及不同加载方式对其破坏形态和抗弯承载力的影响；李婷分析了预应力简支钢梁体外索结构的挠度并给出相关参数关系曲线，研究了其在横向均布荷载作用下弹塑性变形并提出钢梁屈服前后挠度计算公式。相较于简支钢梁，连续钢梁在各种荷载作用下，正弯矩区和负弯矩区产生不同的应力状态，负弯矩区受力较为复杂且影响因素较多。王景全通过对预应力组合梁负弯矩区受力性能进行分析，提出了组合梁负弯矩区抗弯承载力计算方法；肖维思利用有限元软件Ansys对四跨连续梁桥进行模拟计算，分析了连接件布置形式及抗剪刚度对装配式组合梁桥负弯矩区结合部受力性能的影响。目前对负弯矩区受力性能研究多为钢-混组合梁结构，而对预应力连续钢梁负弯矩区的研究尚不充分。

该文首先以一片三跨连续钢梁为研究对象，在其两侧布置高强预应力钢束，形成预应力连续钢梁并进行试验，与普通连续钢梁试验结果进行对比，分析预应力对连续钢梁负弯矩区作用效果。在试验梁基础上，利用有限元软件Ansys建立非线性分析模型，对试验梁加载过程进行数值仿真模拟并与试验结果进行对比，以验证模型的正确性，利用模型对连续钢梁进行进一步的极限状态静力分析，并通过控制参数，分析预应力大小、负弯矩区支座位置处钢束距顶板距离对负弯矩区截面受力性能的影响。

2 试验简介

2.1 试验梁简介

设计制作一开口截面三跨连续钢梁。梁长10 m，跨径组合为(3+4+3) m，钢板厚度4 mm，钢梁截面尺寸见图1。纵向沿桥梁中心线每250 mm设置横隔板，每500 mm设置加劲板。梁体采用Q235钢，弹性模量E=2.06×105MPa，剪切模量G=0.81×105MPa，

图1 钢梁截面尺寸图(单位：mm)

体外预应力钢束采用2束7φ5无黏结钢绞线，公称直径15.2 mm、极限抗拉强度标准值为1 860 MPa。

2.2 加载方案与测点布置

试验采用手摇式千斤顶进行6点同时加载，加载位置为距各跨跨中左右各400 mm处，加载等级按5 kN逐级加载，张拉预应力按19.5、39、58.5、78 kN逐级张拉。

选取试验梁左半部分作为试验段，正弯矩区和负弯矩区是结构控制的重要位置，故在跨中和负弯矩区截面位置布置位移计和应变计。负弯矩区选取支座附近1#～6#共6个试验截面，每个截面布置应变片5个，分布在钢梁顶板、底板及腹板位置。负弯矩区立面钢索布置及测点布置如图2所示。

图2 负弯矩区试验截面应变计测点布置图(单位：mm)

3 有限元数值模拟

3.1 单元参数设置

利用有限元软件Ansys对试验梁按实际加载过程进行数值模拟，采用实体力筋法进行建模。为更加准确分析截面沿厚度方向的应力特征，梁体采用实体单元Solid185，预应力钢束采用杆单元Link180，加载位置建立垫块。该模型采用双线性随动强化准则“BKIN”及Von Mises屈服准则，钢板本构关系采用理想弹塑性模型，屈服强度取235 MPa，钢板本构关系曲线如图3所示，钢束屈服强度取1860钢绞线标准抗拉强度85%，即1 581 MPa。

图3 钢板本构关系曲线

3.2 网格划分及荷载定义

对模型进行自由划分网格，共划分单元138 156个，其中Solid185单元138 116个，Link180单元40个。根据实际加载工况，设置荷载步对模型进行逐级加载；将梁体单元与钢束单元进行节点耦合，采用降温法施加预应力。

4 试验结果及分析

4.1 支座截面沿梁高正应力分布分析

分析负弯矩区在各级荷载作用下的受力状态，普通钢梁及张拉力为19.5 kN时预应力钢梁负弯矩区支座截面(3#截面)正应力沿梁高的变化如图4、5所示。

图4 普通连续钢梁正应力沿梁高分布图

从图4、5可以看出：在试验加载过程中，支座截面正应力沿梁高均呈线性变化，说明对连续钢梁施加预应力后，钢梁在弹性工作阶段截面变形仍符合平截面假定。在相同荷载作用下，预应力钢梁相较于普通钢梁沿梁高各截面正应力均有减小。该试验梁预应力采用了折线布索的形式，钢束在支座截面处上调靠近顶板，使支座位置在张拉预应力后产生上缘受压、下缘受拉的初始应力，与外荷载引起的支座截面应力方向相反，对其有抵消作用。预应力引起支座顶板及底板正应力减小值和百分比如表1所示。从表1可见：在同级荷载下，施加预应力后，顶板应力减小值比底板要大，预应力的施加对负弯矩区支座顶板正应力减小效果更明显。从图5可以看出，张拉预应力后支座截面顶板产生的初始应力较底板大，故抵消效果更明显。

图5 预应力连续钢梁正应力沿梁高分布图

表1 支座顶板、底板正应力减小值及百分比

4.2 支座附近顶、底板正应力分布分析

分析负弯矩区支座附近顶、底板正应力分布规律，普通连续钢梁及张拉力为19.5 kN时预应力连续钢梁负弯矩区1#～6#截面顶、底板应力分布随荷载变化图如图6～9所示。

图6 普通连续钢梁顶板正应力分布图

从图6～9可以看出：施加预应力后，支座附近顶板及底板正应力均有所减小，在30 kN荷载作用下，2#截面顶板正应力减小44.6 MPa，底板正应力减小3.0 MPa，3#截面顶板正应力减小54.2 MPa，底板正应力减小9.8 MPa，可见预应力对负弯矩区顶、底板应力减小效果越靠近支座位置越明显。张拉后梁体产生的初始应力与30 kN荷载作用下1#～6#截面顶、底板应力变化值关系如图10所示。由图10可知：顶、底板正应力变化曲线与初始应力曲线趋势吻合，张拉预应力产生的反向弯矩可以有效抵消荷载作用产生的弯矩，可见预应力对支座顶、底板正应力变化影响效果取决于张拉预应力后梁体的初始应力。

图7 预应力连续钢梁顶板正应力分布图

图8 普通连续钢梁底板正应力分布图

图9 预应力连续钢梁底板正应力分布图

5 有限元结果分析

5.1 有限元结果与试验对比分析

根据试验结果分析负弯矩区在试验加载过程中截面的受力性能，该文在一定数量试验的基础上，建立了Ansys有限元分析模型，进而对负弯矩区受力主要影响因素进行分析，对复杂试验过程进行有效简化。Ansys模型计算值和实测的钢梁挠度及负弯矩区支座截面顶、底板正应力值如表2、3所示。由表2、3可知：有限元计算结果与试验结果吻合良好，说明该文利用Ansys对预应力连续钢梁数值仿真模拟方法合理准确。

5.2 极限状态静力分析

利用Ansys模型对连续钢梁进行全过程静力分析，确定其极限荷载，并分析极限荷载作用下负弯矩区受力状态。普通钢梁及张拉力为80 kN时预应力钢梁荷载-位移曲线如图11所示。

从图11可以看出：在加载初期，荷载-位移曲线基本呈线性关系，随着荷载增大，曲线斜率开始变化并逐渐增大，梁体有部分截面进入屈服状态，此时钢梁达到弹性极限抗弯承载力，继续增大荷载，挠度曲线出现明显拐点，位移剧增，当跨中挠度达到计算跨径的1/200时，视其达到承载能力极限状态。普通连续钢梁及预应力连续钢梁所对应弹性极限荷载分别为35、45 kN，利用Ansys模型计算各自在该荷载作用下支座及跨中截面正应力如表4所示。

表2 各控制截面钢梁挠度试验结果与Ansys计算值

表3 支座截面顶板及底板正应力试验结果与Ansys计算值

图11 普通连续钢梁及预应力连续钢梁荷载-位移曲线图

表4 负弯矩区支座及跨中位置截面正应力

由表4可知：支座底板应力先达到屈服强度，此时支座顶板及跨中顶、底板应力均未达到屈服。随着荷载增加，支座截面部分进入塑性，中和轴附近仍处于弹性状态，继续增大荷载截面变形发展较快，实际很难达到全截面塑性，梁体因挠度过大而不能承受更大荷载。预应力连续钢梁负弯矩区应力塑性发展过程如图12所示，支座截面应力图12(d)可由预应力张拉后初始应力图12(b)和裸梁应力图12(c)叠加得到，可见施加预应力后，梁体产生与荷载应力相反的初始应力，改变了结构受荷载前的应力场，通过抵消作用扩大了结构的弹性受力范围，进而提高了结构的承载力。

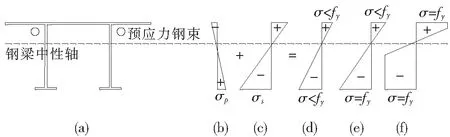
图12 支座截面塑性应力发展过程

5.3 预应力大小对支座截面顶底板正应力影响分析

分析预应力大小对负弯矩区顶、底板正应力的影响，预应力H分别取60、80、100、120 kN，支座截面顶、底板应力-荷载曲线随预应力变化的影响如图13、14所示。当支座底板应力达到屈服极限时，预应力连续钢梁达到弹性极限荷载，利用Ansys模型计算不同初始预应力下预应力连续钢梁的弹性极限荷载如表5所示。

图13 预应力大小对支座截面顶板应力-荷载曲线的影响

图14 预应力大小对支座截面底板应力-荷载曲线的影响

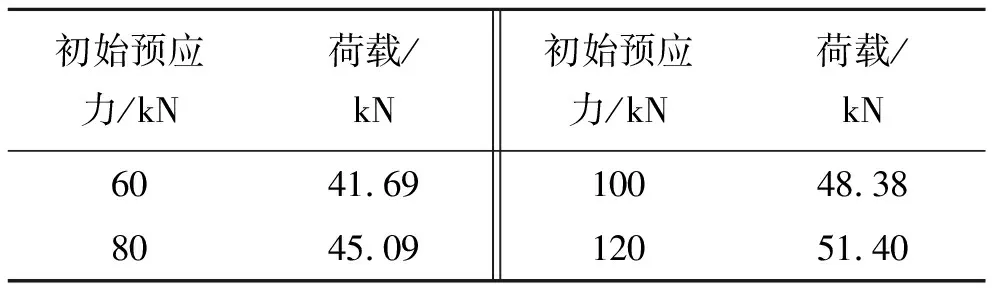
表5 不同初始预应力下预应力连续钢梁弹性极限荷载

从图13、14可以看出：顶板及底板正应力均随预应力增大等比例变化，预应力每增加20 kN，同级荷载下顶板正应力减小约34.4 MPa，底板正应力减小约25.3 MPa，预应力大小对负弯矩区应力变化呈线性正比例关系，且预应力对顶板正应力影响更明显。从表5可知：当预应力由60 kN增大至120 kN时，弹性极限荷载由41.69 kN增大至51.4 kN，提高约23.3%，可见预应力越大，其抵消负弯矩区荷载应力的效果越显著。但同时增大预应力也会导致张拉后截面初始应力相应增大，从表6可以看出：当预应力超过135 kN时，支座顶板应力在张拉阶段即达到235 MPa进入屈服状态，故张拉力有一定限度，不宜过大，在不超过135 kN范围内，合理增大预应力可以线性提高预应力连续钢梁负弯矩区抗弯承载能力。

5.4 支座截面钢束距顶板距离对顶、底板正应力影响分析

预应力钢束的布置对结构受力会产生影响，可通过上调负弯矩区钢束使结构受力更加合理。简支转连续混凝土T梁桥负弯矩束距顶板距离对负弯矩区产生较大影响，随着负弯矩束距顶板距离的增大，预应力引起负弯矩截面次弯矩有减小趋势。分析预应力连续钢梁支座截面钢束距顶板距离h对负弯矩区受力的影响。分别取h=15、20、25、30、35 mm进行计算，支座附近截面顶、底板正应力变化值受h的影响如图15、16所示。从图15、16可见，随着支座截面钢束上调，负弯矩区顶、底板正应力均有减小，顶板正应力变化略明显，且越靠近支座位置正应力减小值越大，最大达到15.2 MPa，负弯矩区顶板受拉段长度也将随之减小，故在支座截面钢束布置越靠近顶板，对负弯矩区受力越有利，这与文献[13]结论相一致。