带电圆面场强公式适用范围的分析与探讨**

王丽娜 赵兴宇

(伊犁师范学院物理科学与技术学院 新疆 伊宁 835000)

1 引言

带电平面的电场场强是电磁学中的一个重要问题，带电平面是理论和实际问题中的一个重要理想模型，也是处理平行板电容器、导体和介质表面附近电场的重要基础[1～4]，对均匀带电平面及其相关问题的研究仍在继续[5～7].均匀圆形带电平面(带电圆面)在其轴线上产生的场强可通过积分求出，任意形状带电平面附近的场强可通过高斯定理求得[3].当分别满足一定条件时，带电圆面可简化为无穷大带电平面或点电荷问题，但是究竟场点到圆面的距离比圆面尺寸小到多少时，才可以把带电平面在其轴线上产生的场强看成无限大均匀带电平面的结果，究竟大到多少时可以简化为圆心处等量点电荷.而且，当场点到均匀带电面的距离趋近于零时，面上的一些电荷到场点的距离将趋近于零，由点电荷的场强公式可知，该点的场强将会是无穷大；然而此时，无论是带电圆面在其轴线上的场强公式，还是无限大均匀带电平面的场强公式，都相同地给出了一个与距离无关的有限值，这与由点电荷的观点得出的结论是相矛盾的；造成这种矛盾的原因又是什么呢？这一矛盾将直接影响面附近场强问题的处理.

为了增强对带电平面问题的理解，便于场强公式的选择运用，本文将采用数值计算的方法对上述问题进行研究，给出定量标准下公式的适用范围，分析产生矛盾的原因.

2 带电圆面模型的构建与理论

在微观上，电荷的分布是离散的、不连续的，所以建立模型时，在微观尺度上电荷是以离散形式进行分布的.假设有一个圆面位于z=0的平面内，圆心位于坐标原点，如图1所示.

由点电荷场强公式可知，格点(ia,ja,0)上的电荷在P(x,y,z)点产生的场强为

(1)

式中ε0为真空的介电常数，π为圆周率，rij为格点(ia,ja,0)到P点的距离，erij为格点(ia,ja,0)指向P点的单位矢量.依据几何关系可以得到

(2)

由场强的叠加原理可知，场点P(x,y,z)处的场强ES(x,y,z)为

(3)

(4)

(5)

(6)

3 计算结果与分析

3.1 带电圆面轴线上场强公式的适用范围

在考察z→0，P(0,0,z)处点电荷公式的直观结果与式(4)、(5)结果相矛盾情况时，考虑到微观上电荷分布不连续，分别模拟计算了n为奇数[轴线过格点(0,0,0)]和n为偶数[轴线过格点(-0.5a,-0.5a,0)和(0.5a,0.5a,0)连线的中点]的两种情况，以便观察微观上电荷分布不连续所产生的影响.

图2所示的是模拟结果ES和理论结果EI随z的变化情况，(a)和(b)分别是n为奇数和偶数的情况，主图是局部放大的结果，插图是全部结果.

图2 模拟结果ES和理论结果EI随z的变化

图3 相对偏差随z的变化

从图2中可以看出，在模拟的所有体系中，在z较小时，ES和EI的差别都比较明显，但是随着z的增加，ES和EI逐渐趋于一致.

为了探究图2(a)中在z较小时，引起较大偏差的原因，这里将n为奇数时，格点(0,0，0)的电荷在P(0,0,z)点所产生的场强EO进行单独计算，并与由式(3)计算所得的整个圆面所产生的场强进行对比，如图4所示.可以看出在z较小时，EO几乎与EI一样，这说明此时其他电荷在P点所产生的场强要远远小于EO，也就是说格点(0,0，0)处电荷的贡献超过其他电荷的总和，EI被格点(0,0，0)处电荷的个体性所主导，而带电圆面的整体性被淹没了.

图4 ES和EO随z的变化

图5 相对偏差随z的变化

所以，ES和EI之间的差别是由微观尺度下电荷的离散分布和单个电荷对场强的贡献过大造成的.通常情况下，所说的“均匀”带电，实际上指的是宏观均匀.以99%相对精度为例，式(4)在z≥a的空间尺度内适用，在z≥1.1a的尺度下可认为电荷是连续均匀分布的；当z=2a时，EI的精度高达99.99%，z在宏观尺度时，式(4)的结果可认为是精确的.

3.2 带电圆面轴线上场强可简化为无限大均匀带电平面场强的条件

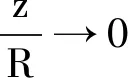
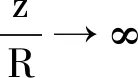
(7)

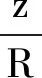
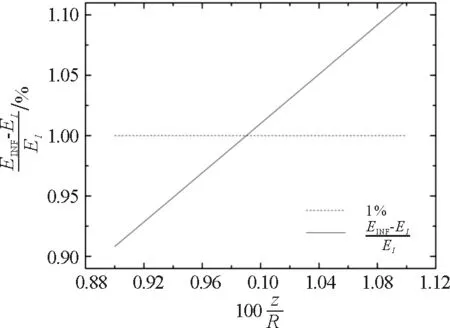
图6 相对偏差随的变化

3.3 带电圆面可以简化为圆心处等量点电荷的条件

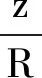
(8)

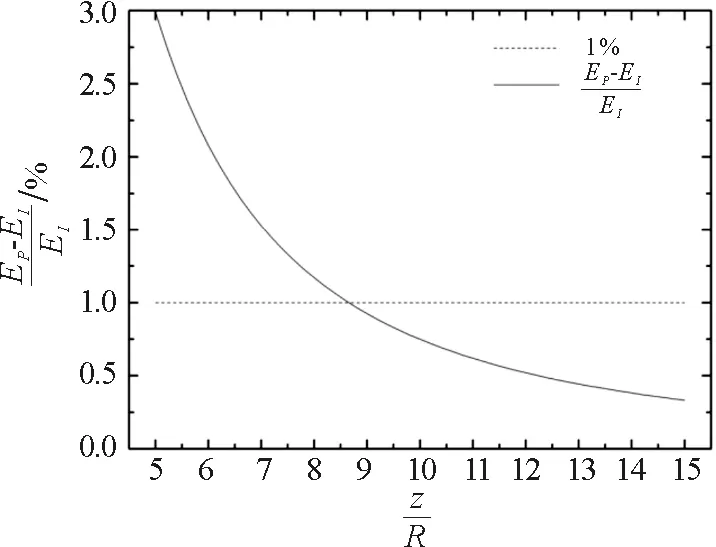
图7 相对偏差随的变化

通过对以上两个方向的分析可看出，为了方便，这里可取场点到圆面圆心的距离大于10R时，将带电圆面产生的电场看成是圆心处等量点电荷，其场强的相对精度可达到99%以上.

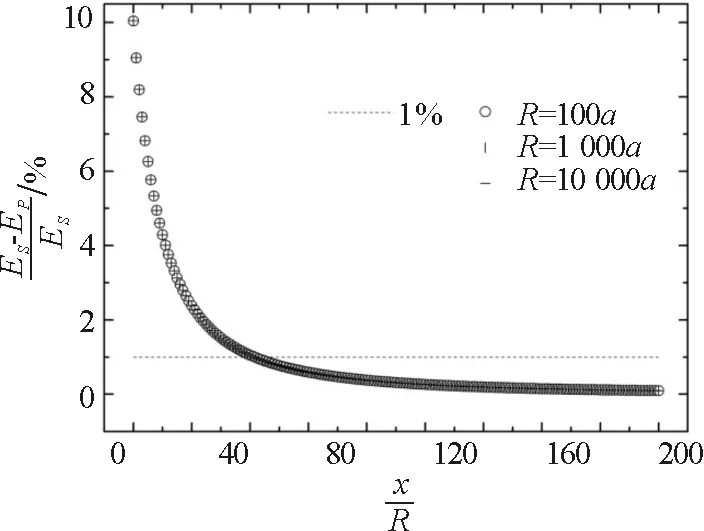
图8 相对偏差随x的变化

4 结论

通过计算分析表明，当场点到圆面的距离在电荷间距的尺度下时，带电圆面轴线上场强公式的相对偏差较大，但随着距离的增加快速减小，逐渐与精确值一致，偏差是由微观尺度下电荷的离散分布和单个电荷对场强的贡献过大造成的.以99%的相对精度为例，场点到圆面的距离大于电荷间距时，带电圆面轴线上场强公式可以适用；场点到圆面的距离大于1.1倍的电荷间距时，可以认为电荷是均匀连续分布的；场点到圆面的距离大于1.1倍的电荷间

距且小于圆面半径的1%时，带电圆面轴线上场强公式可以简化为无限大带电平面的场强公式；场点到圆心的距离大于圆面半径的10倍时，带电圆面可简化为圆心处等量点电荷的结果.本文计算场强的方法和思路，可以推广运用到带电圆面在任意点所产生场强的计算.