一种新的基于脑电信号相似性分析的癫痫性发作自动检测方法

李斯卉, 吕可嘉, 潘 敏, 张 瑞

(1.西北大学 医学大数据研究中心，陕西 西安 710127； 2.西安交通大学 医学部,陕西 西安 710061)

癫痫是最常见的神经功能障碍之一,世界范围内的患病率接近0.9%。其最主要的临床症状表现为癫痫性发作,通常是由大脑内大量神经细胞群异常超同步放电所引起。脑电图(Electroencephalogram,EEG)通过追踪和记录脑电波来呈现大脑的放电活动,是目前用于检测癫痫性发作等神经功能障碍异常脑电模式的有效手段。然而,传统的癫痫诊断往往需要专业医师依据经验对长时程脑电图通过视觉上的检查来完成,这一过程不仅耗时、主观性强,而且大量噪声的存在也使得这一工作极具挑战。因此,近几十年来,越来越多的研究者开始致力于开展癫痫性发作自动检测的研究。

神经学家的近期研究结果表明,人的大脑可以看作是一个非线性动力系统。基于此,各种建立在非线性方法基础上的癫痫性发作自动检测方法被相继提出。从分析系统混沌性的角度出发,Beyli等人计算脑电信号的Lyapunov指数作为特征,并应用多层感知器神经网络(MLPNN)来实现癫痫性发作的自动检测[26]。基于系统复杂性分析,Zhang 等人结合分形维数和梯度增强提出了一种癫痫自动检测方法[28],Song 等人提出了一种基于模糊条件Renyi熵的癫痫性发作自动检测方法[24]。除此之外, Zhou 等人提出了一种基于小波变换的癫痫性发作检测方法,该方法提取残差和波动指数作为特征且应用贝叶斯线性判别分析(BLDA)作为分类器[29]。Li等人在文献[16] 中定义了脑电信号三维相空间表示的核半径,并以此作为所提取的特征结合超限学习机和支撑向量机完成发作的自动检测[16]。在文献[7] 中,Chen等人从EEG子带信号中提取了近似熵、递归量化分析和样本熵三个非线性度量,并将其融合特征作为支撑向量机和超极限学习机的输入以完成癫痫性发作的自动检测。在非线性相互依赖性分析方面,Song 等人提出了基于庞加莱散点图的特征,通过刻画延迟庞加莱散点图的分散程度和分布一致性并结合ELM完成自动检测[23]。为了分析系统的高阶统计特性,Acharya等人用高阶谱(HOS)结合SVM来区分正常、发作期和发作间期的EEG信号[1]。此外,用模糊相似性指数[14]和动力学相似性指数[17]对脑电信号的非线性时空演变进行分析,且被用于分析发掘从非癫痫状态到癫痫发作状态之间的过渡。在文献[22] 中,Song等人提取了基于马氏相似度的特征并进一步结合样本熵进行特征融合,最终采用超限学习机完成癫痫检测。

本文提出了一种新的脑电信号相似性的分析方法,并进一步探讨了其在癫痫性发作自动检测中的应用。首先根据时间延迟方法计算脑电信号的轨迹矩阵(TMS);其次,通过对轨迹矩阵进行奇异值分解(SVD)定义脑电信号的特征表示向量(FRV);进而,基于信号的特征表示向量计算待测脑电与模版脑电之间的最大余弦相似度(MCS),并将其定义为所提取的癫痫脑电特征;最后,将所提取特征输入到分类器中完成癫痫性发作的自动检测。

1 方 法

1.1 相空间和轨迹矩阵

动力系统可以通过一组状态以及状态间的转换规则来描述[13]。系统的状态通常以向量形式表示,而状态向量的集合则定义为系统的相空间。我们可以通过评估其相空间来研究系统的动力学特性[15],然而在大多数情况下,一个系统的相空间很难直接获取。基于此,通过所记录的系统输出信号来重建该系统相空间的不同重建方法被相继提出,其中时间延迟法是应用最为广泛的一类[25]。

给定时间序列s={s1,s2,…,sN},其相空间可以由下式表达:

A={A1,…,Aj,…,AL}T

(1)

Aj={sj,sj+τ…,sj+(m-1)τ}T。

(2)

其中m表示嵌入维度,τ为时间延迟,L=N-(m-1)τ。由于重构的相空间A以矩阵形式表示,因此A也称为信号s的轨迹矩阵(trajectory matrix,TM)。需要强调的是,参数m和τ的选择非常重要。本文采用互信息法(MI)确定参数τ的取值[4],并根据参考文献[5] 中的方法确定m的取值。

1.2 EEG信号的特征表示向量

奇异值分解是最具代表性的一类矩阵分解方法,在机器学习的算法中占有重要地位[20]。

给定EEG信号s={s1,s2,…,sN}。根据式(1)和(2)可得到s的轨迹矩阵

则矩阵A的奇异值分解可表示为

(3)

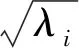
注1除SVD分解外,常用的矩阵分解方法还包括LU分解,Cholesky分解,QR分解和LDLT分解等。其中Cholesky分解和LDLT分解均假设矩阵是正定的,QR分解假设矩阵是方阵且非奇异的。因此,针对本文的研究对象EEG信号,LU分解也可用来获得EEG信号的特征表示向量。数值实验结果表明,奇异值分解在完成癫痫性发作检测方面优于LU分解(见表4)。因此,本文所提方法中采用奇异值分解。

1.3 EEG信号间的最大余弦相似度

余弦相似性(cosine similarity,CS)通过在内积空间中计算两个非零向量夹角的余弦值来度量其相似性。给定两个非零向量x=(x1,x2,…,xn)T和y=(y1,y2,…,yn)T,则x与y之间的余弦相似性定义为:

(4)

其中θ为x与y之间的角度,x·y表示x与y的内积,‖·‖表示向量长度。在此基础上,可进一步将其扩展为度量两个矩阵之间的相似性。具体地,给定两个具有相同阶数q×n的矩阵X=(x1,x2,…,xn)q×n和Y=(y1,y2,…,yn)q×n,其中x1,x2,…,xn和y1,y2,…,yn分别是X和Y的列向量。对于每对列向量xi和yj,根据式(6)计算它们之间的余弦相似性CS(xi,yj),则有

MX,Y=

定义2设X和Y是两个同阶矩阵,定义

(5)

为X和Y之间的行最大余弦相似度(MCS-R),其中

(6)

同理,定义

(7)

为X和Y之间的列最大余弦相似度(MCS-C),其中

(8)

注2在定义2中,行最大余弦相似度MCS-R和列最大余弦相似度MCS-C显然满足MCS(r)(Y,X)=MCS(c)(X,Y)。

注3在定义2中,如果两个矩阵不满足同阶但具有相同的行数(或相同的列数),则可同理定义它们之间的行(列)最大余弦相似度。

结合定义1和定义2,我们进一步刻画两个EEG信号之间的相似性如下。

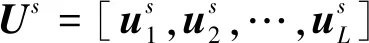
MCS(s,t)=MCS(r)(Us,Ut)

(9)

为s和t的最大余弦相似度,且

MCS(t,s)=MCS(c)(Us,Ut)

(10)

为t和s的最大余弦相似度。

1.4 基于EEG信号相似性分析的癫痫性发作自动检测方法

在上述工作的基础上,本小节提出一种新的基于最大余弦相似度的癫痫脑电特征,并结合有效的分类器以完成癫痫性发作的自动检测。该方法总结为以下TFM-SZ算法。

算法Ⅰ(TFM-SZ算法) 令S={s1,s2,…,sΓ}为脑电信号集合,其中si={si,1,si,2,…,si,N}表示第i个脑电信号,Γ表示S中脑电信号的总数。

步骤2构建参考脑电信号。

1)从S中随机选取p个发作间期脑电信号,记为{si1,si2,…,sip},其中p小于S中的发作间期脑电信号总数;

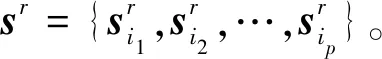
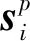
步骤4计算参考脑电信号与每个待测脑电信号之间的最大余弦相似度。

对于i=1:Γ

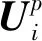
End

步骤5定义癫痫脑电特征(TFM-F)为

(11)

步骤6将提取的特征F输送到某个分类器中。

TFM-SZ算法的流程图如图1所示。

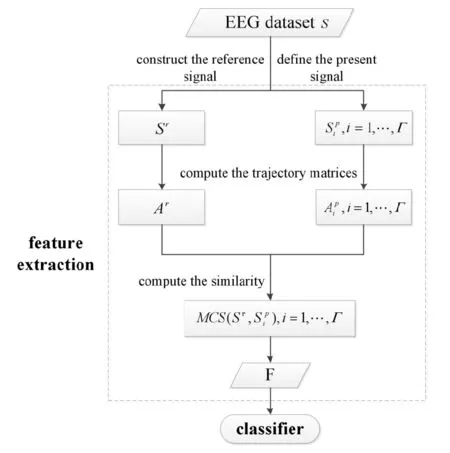
图1 TFM-SZ算法的流程图Fig.1 The flow chart of TFM-SZ Algorithm

2 数值试验结果与分析

2.1 脑电数据

本文数值实验中使用的脑电数据来自两个数据库:Bonn数据库和CHB-MIT数据库。Bonn数据库的详细信息如表1所示,图2展示数据集D和数据集E的两个脑电片段(单通道)。CHB-MIT数据库采集自波士顿儿童医院,采集自22名患有难治性癫痫的受试者(17名女性,年龄为1.5～19岁;5名男性,年龄为3～22岁)。共包含664个脑电图记录,采样率为256Hz,分辨率为16bit,大多数脑电信号为23通道(个别记录为24或26通道)。图3展示了来自CHB-MIT数据库中“记录chb03”的一个23通道的脑电片段。

表1 BONN数据库的详细信息Tab.1 Details of BONN database

注：①BONN数据库取自德国BONN大学癫痫系[2,24];②每个数据集包括100个单通道脑电图,采样率为173.61Hz,每个脑电图段持续23.6s;③所有EGG都没有造假。

图2 BONN数据库的EEG片段Fig.2 Sample EEG recordings from Boon database

2.2 结果与分析

在数值实验中,我们从Bonn数据库的数据集D中随机选择p=30个发作间期脑电信号,再从每个信号中随机选取持续时长为10s的脑电片段(即d=173.6×10=1 736)。在特征值TFM-F的计算过程中,设定嵌入维数m=5和延迟时间τ=1。在超限学习机(extreme learning machine,ELM)[10]中,采用可加性隐节点G(a,b,x)=g(ax+b),隐节点参数(a,b)服从均匀分布随机选取,通过十倍交叉验证选择隐节点个数为80。在支持向量机(support vector machine,SVM)[9]中,使用最新的Libsvm软件包3.22版本,核函数选取径向基函数。根据网格搜索法,正则参数C和宽度g取为(2-4,2)。所有的实验均在Matlab 9.1.0中运行。

图3 CHB-MIT数据库的EEGFig.3 Sample EEG recordings from CHB-MIT databse

2.2.1 Bonn数据库上的性能验证 本文提取了一个新的基于相似性分析的癫痫脑电特征TFM-F,并将其用于实现发作期脑电、发作间期脑电和正常脑电的分类与检测。

首先，验证所提取特征TFM-F分别结合ELM和SVM在完成癫痫性发作自动检测中的性能。在执行SVM和ELM的过程中均进行50次测试,每次测试随机生成个数均衡的训练集和测试集[24]。表2列出了性能的比较结果,包括分类准确率(ACC)、标准差(Std)、训练时间(training time)和参数选择时间(parameter selection time)。从表2可看出,ELM相比SVM,分类准确率略高一点,然而其标准差更小,这表明ELM比SVM的分类性能更加稳定。同时,ELM的训练时间仅为SVM的1/430。由于ELM具有较好的分类性能,因此在进一步的数值实验中我们均采用ELM作为分类器。

其次，比较两种矩阵分解方法以及5种相似性度量在特征提取中的性能。表3,4中结果可展示所提方法的优良性能,包括敏感性(SEN),特异性(SPE),精度(PRE)和准确率(ACC)[22]。从表3可以看出,由“TFM(SVD)+ELM” 方法得到的敏感性,特异性,精度和准确率均远远高于通过 “TFM(LU)+ELM”方法所得到的值。此外从表4可知,与其他4种相似性度量方法相比,“TFM(Cosine)+ELM”的性能表现最好。上述结果表明,本文特征提取算法中所采用的SVD分解和余弦相似性最为有效。

表2 “TFM-F+ELM”和“TFM-F+SVM”的性能比较Tab.2 Performance comparison between "TFM-F+ELM" and "TFM-F+SVM" on BONN database

注:运行时间=训练时间+参数选择时间。

表3 特征提取中两种矩阵分解LU和SVD的性能比较Tab.3 Performance comparisonbetween LU and SVD in extraction the feature TFM-F

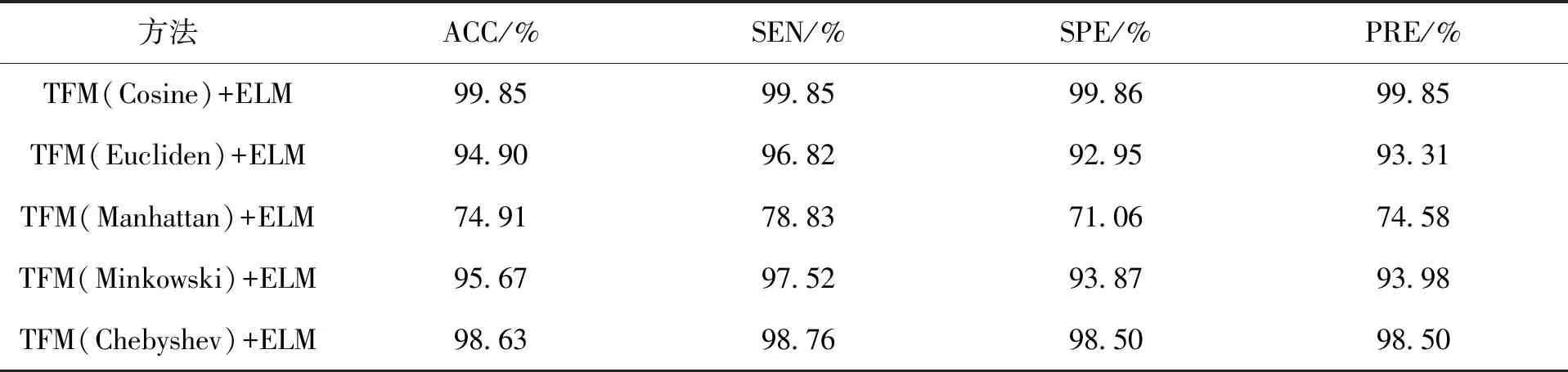
表4 特征提取中5种相似计算的性能比较Tab.4 Performance comparison between consine similarity and other four similarity measures in extracting the feature TFM-F

然后对本文所提取特征TFM-F与模糊相似性指数(FSI)和样本熵(SE)的性能进行系统比较。从表5可以看出,与FSI和SE相比,本文所提取特征TFM-F的性能有明显提高。具体来说, TFM-F的漏检率和误报率均达到0.15%,与 FSI的结果相比分别减少了近55倍和45倍。此外,FSI所耗费的训练时间是本文所提方法的44倍左右。另一方面,虽然SE所耗费的训练时间只有TFM-F的三分之一,但其漏检率和误报率分别比TFM-F升高了近3倍和20倍。此外,本文采用ROC曲线更为直观地比较上述3个特征的性能(见图4),显然TFM-F的AUC(ROC曲线下方包围的面积)最大,表明其检测性能最好。

最后将本文所提出的自动检测方法TFM-SZ和已有6种自动检测方法进行比较(所有结果均采用相同数据集)。从表7可以看出,本文方法将准确率从97.53%提高至99.85%。

图4 3个特征TFM-F,FSI和SE的ROC曲线Fig.4 ROC curves for three features TFM-F, FSI and SE

特征ACC/%SEN/%SPE/%PRE/%TFM-F+ELM99.8599.8599.8699.85FSI+ELM93.6491.7593.1092.03SE+ELM96.9499.6294.2994.51

2.2.2 CHB-MIT数据库上的性能验证 本小节采用CHB-MIT数据库中的头皮脑电数据,验证所提癫痫性发作自动检测方法TFM-SZ的性能。这一数据库中的脑电信号含有大量伪迹并具有严重的数据不平衡现象,因此会给自动检测的有效实现带来更大困难。然而,这样的挑战在临床应用中却具有重大的现实意义。本文选取了来自CHB-MIT数据库中5名患者的脑电数据进行数值实验。表6中详细列出了上述数据的详细信息,包括记录时间、发作次数和发作持续时间。采用小波软阈值法去除伪迹,其中选用4阶Daubechies小波作为小波母函数进行5层分解。通过重叠时长为3s的滑动窗口,把所有去噪后的脑电信号分割成5s长的脑电片段并将这些片段随机分为个数相同的训练集和测试集。考虑到CHB-MIT数据库中发作数据和非发作数据的严重不平衡,本文采用敏感性和误报率(FDR)来评估算法性能,计算公式如下:

敏感性=发作检测正确的次数/发作的总次数,

误报率=发作检测错误的次数/记录总时长。

表6中展示的实验结果包括检测正确的次数、检测错误的次数,敏感性和误报率。可以看出,只有患者“chb03”出现了一次错误检测,其误报率为0.0625。此外,在患者“chb08”(女,3.5岁)8h的脑电图记录中共出现了两次发作,但本文所提方法仅成功地检测出一次发作,敏感性为50%,这一结果很可能是由该患者年龄过小所造成的。

表6 所提自动检测方法TFM-SZ在CHB-MIT数据库上的性能评估Tab.6 Performance evaluation of the proposed method TFM-SZ on CHB-MIT database

表7 TFM-SZ的建议方法和BONN数据库上的其他现有方法的性能比较Tab.7 Performance comparison among the proposed method TFM-SZ and other existing methods on BOON database

3 结 论

本文提出了一种新的脑电信号相似性的分析方法,进而在这一方法的基础上定义了待测脑电与模版脑电之间的最大余弦相似度为癫痫脑电特征,并将其应用于癫痫性发作的自动检测。文中从三个方面验证了所提癫痫检测方法TFM-SZ的性能:①所提取特征TFM-F的性能评估(Bonn数据库),包括两个矩阵分解方法LU 与SVD的性能比较、余弦相似度与其他四种相似性度量方法的比较、以及3个特征间的性能比较;②所提出癫痫性发作自动检测方法TFM-SZ的性能评估(Bonn数据库和CHB-MIT数据库),包括两个分类器ELM和SVM的性能比较,所提方法TFM-SZ与其他6种已有方法的性能比较,以及TFM-SZ针对原始采集的头皮脑电数据上的检测性能验证。所有数值实验结果表明,本文所提出的脑电信号相似性分析方法可以成功应用于癫痫性发作的自动检测。