研读试题 分步递增 跳出题海 提升素养*
——以2018年浙江省温州市数学中考第15题为例
2019-04-15
●
(乐成公立寄宿学校,浙江 乐清 325600)
1 “一题一课”复习课模式的理念与实施
1.1 常规复习课的不足之处和解决办法
常规的一节中考复习课,教师通常是以一个知识板块或章节内容为主题,搜集很多的例题,在复习基础知识时,先让学生解决很多问题,再引出复习的主题.这样的方式开展复习,知识点全面、教学目标指向明确,但是这样的复习课,大量的审题和理解占去了大部分时间和精力,后续的提高部分,时间和精力上就显得捉襟见肘,复习课在低效进行.那么有没有一种既可以全面复习知识点,又有大量的时间和精力进行后续拓展提升的复习课?能不能在知识回顾的阶段融入知识点的“四基”能力培养和提高,在问题解决中提炼数学模型和思想方法,使得复习课更加有效地进行呢?显然,这样的想法是可以实现的,通过“一题一课”复习课的模式,选用一个问题,比如选用一个往年的中考试题进行深入分析,通过条件的分解,从最基础的条件提出第一个问题,然后按顺序逐渐增加条件,不断提出新的问题;每个问题的提出都设置开放结论,学生回答并说明理由,提炼数学模型和思想方法,最后呈现原题,提倡一题多解,对比参考,落实“四基”,提高“四能”,提升核心素养.
1.2 “一题一课”的教学模式
“一题一课”复习课就是教师通过对一道题(或一个材料)的深入研究,挖掘其内在的学习线索与数学本质,基于学情,科学、合理、有序地组织学生进行相关的数学探索活动,从而完成一节课的教学任务,以此达成多维目标的过程[1].在选择“一题一课”的“一题”(本文称之为“原题”)时要注意把握以下选择原则:问题浅入深出,有一定的知识容量,涉及多种数学思想方法,学生思维能得到真正锻炼;问题具有层次性,可以让不同学生在学力上得到不同的发展;问题具有开放性,即探究过程和结果呈开放姿态,让不同层次的学生都能参与,同时又能得到不同的发展[2].
1.3 分步递增条件呈现原题的步骤与方法
通过深入分析原题,把条件进行分解,分清前后顺序,从最简单的条件开始,编制新题,提出开放性问题,并追问结论成立的依据和推理过程;再逐渐添加条件,每一次添加条件后,对应提出新的开放性问题;最后呈现原题.每次问题的解决都提炼基本图形、思想方法和数学模型.
以下选用2018年浙江省温州市数学中考试题第15题,谈谈怎样通过“一题一课”复习课模式开展复习课基础知识回顾部分的复习.
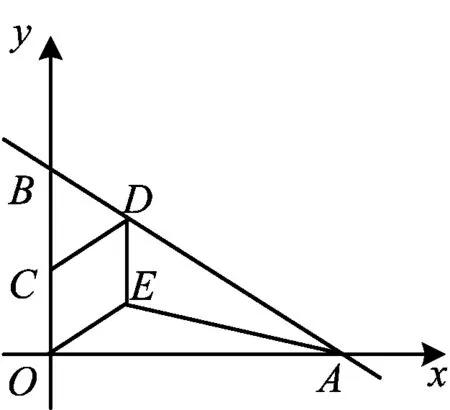
图1
2 中考原题与分析
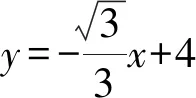
(2018年浙江省温州市数学中考试题第15题)
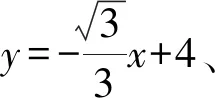
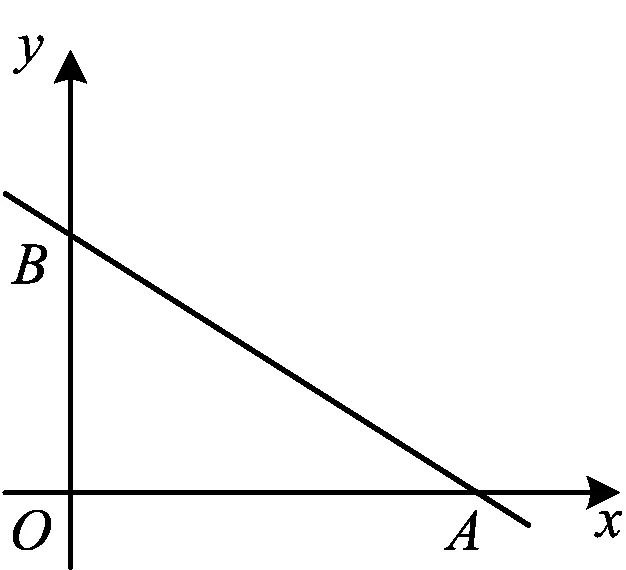
图2
3 教学课例与设计意图
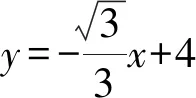
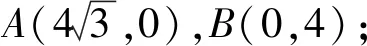
3)角的度数:∠OAB=30°,∠OBA=60°;
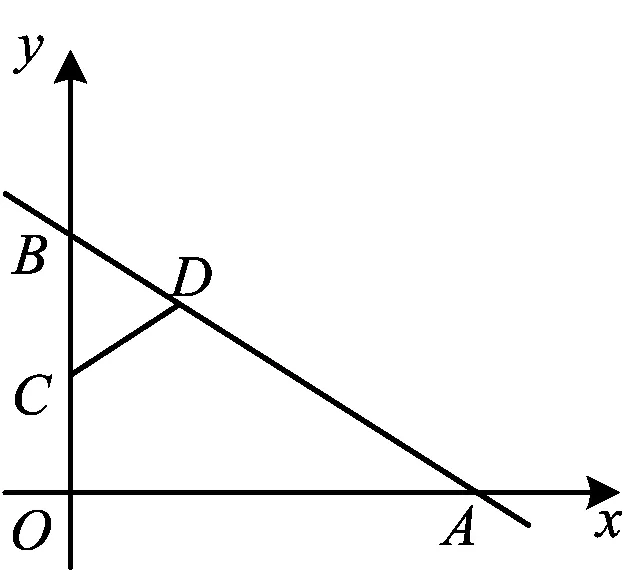
图3
设计意图问题1涉及一次函数性质、交点坐标的求法、特殊角三角函数、勾股定理和直角三角形面积计算等.通过开放性问题,促使学生全方位思考一次函数条件下可以得到的数学结论,并形成坐标体系下从点、线、角、面这4个角度思考问题的习惯;通过追问,学生需要说出每个结论的推理依据和解题思路,形成推理习惯;在计算过程中巩固数学模型、基本图形和基本算法,形成技能,为下一步解决更多问题做好准备.这样低起点、开放性的问题呈现方式,全面开展基础知识复习,有效培养学生各方面的能力.
问题2(增加条件)如图3,C是OB的中点,D是AB上一点,OC=CD,你能得到什么结论?
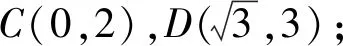
2)线段长度:BD=CD=BC=2,AD=6;
3)角的度数:∠BCD=∠CDB=∠DBC=60°,∠OCD=∠CDA=120°;
设计意图问题2增加了条件“C是OB的中点,D是AB上一点,OC=CD”,涉及等边三角形判定、高及面积计算等数学“四基”能力,还拓展到互补、线段大减小、面积大减小的间接计算等数学计算模型和方法;在等边三角形面积计算的过程中涉及构造辅助高,形成基本图形的提炼与运用.看似只增加了一条线段CD,却能产生挖掘出更多数学能力培养的机会,逐步培养学生的核心素养.
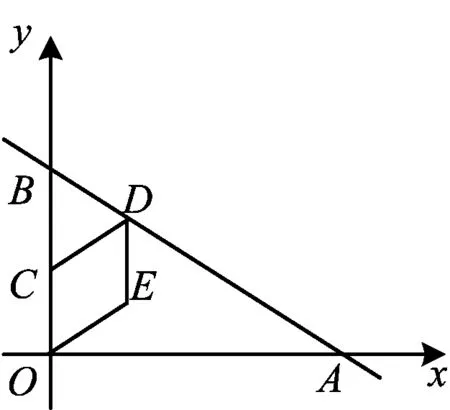
图4
问题3(增加条件)如图4,以OC,CD为边构造菱形OEDC,你能得到什么结论?
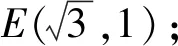
2)线段长度:DE=OE=2;
3)角的度数:∠COE=∠CDE=60°,∠OED=120°;
设计意图问题3增加了条件“菱形OEDC”,涉及菱形的性质、高和面积的计算等数学“四基”和“四能”,还拓展到菱形面积计算等多种计算模型和基本图形.解题方法上提倡一题多解,多角度挖掘数学问题的深层次元素,以学定教,提高复习的有效性.

图5
问题4(增加条件)如图5,联结AE,求△OAE的面积(例1).
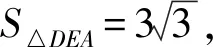
S△OEA=S△ABC-S△BCD-S四边形EDCO-S△DEA=
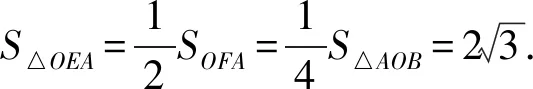
设计意图通过前3个问题的积累和铺垫,学生从开放性结论的问题中逐渐形成思维习惯,自然而然会从点、线、角、面体系中提出问题和进行计算推理,这样递增条件的方式可以尽可能多地涉及“四基”知识、计算和推理的锻炼、基本图形的提炼和构图能力的提升、数学思想方法的培养,从而有效促进核心素养的全面提升.
4 收获与思考
1)研读试题,分析条件构成;结合复习课目标,以学定教;提升教师素养和能力.
“一题一课”既是一种高效的复习课模式,也是一种有效的主题教研活动,教师通过“一题”结合教学目标设计课堂,通过研究和剖析“一题”,理顺问题中的条件构成和相互联系,以学定教,确定条件的分步递增顺序,这样的备课既能促使教师研究试题,又能促进教师研究课堂,是一项很好的校本教研范式,能够有效提高教师的素养和能力.
2)分步递增,一题多变;设置结论开放问题,引领学生夯实“四基”,提高“四能”.
通过递增条件,分步呈现问题,一题变多题,问题层层递进设计,课堂中随着问题的呈现和解决,原有的知识记忆被激活,从而有效开展复习.本文例题涉及一次函数的性质、简单三角函数性质、等边三角形边角关系、勾股定理、一般三角形面积计算等数学知识与应用,促使学生全方位探寻问题结论,不断深化,使学生原有的认知经验转化成学生知识探究的出发点和知识建构的支撑点,夯实“四基”;提出的开放性问题可以让不同层次的学生经历数学知识的形成与应用过程,也能使学生自然地进入自主探索与合作交流学习之中,建立合作与交流、发现与验证、运用与操作的高效课堂,能让学生对问题结论从广度上不断思考、发现,促使学生思维全面发展和“四能”提高.
3)跳出题海,激发兴趣;减负增效,提升复习课课堂效率.
复习课的课堂,大量堆积例题和练习,学生在题海中绞尽脑汁,苦恼不已.但教学的减负增效从来就不是一句空话,通过“一题一课”复习课模式,采取“一题”的引入,省去大量审题和分析的过程,跳出题海,把时间和精力用在开放性结论的寻找和验证中,学生根据自身的基础能力得到对应的数学结论,自身的基础得到对应的发展,自然会激发学生的学习兴趣,增加课堂学习效率,有效落实课堂教学目标.
4)提炼基本图形,归纳数学思想,增强学生的建模能力,提升学生的核心素养.
本文例题中蕴含了一次函数与坐标轴相交、直角三角形基本图形、等边三角形高和面积计算、平行四边形高和面积计算、三角形高和面积计算的基本图形.
例题还涉及了数形结合思想、转化思想、特殊到一般思想、类比思想和数式通性等,学生运用观察分析、数学抽象、逻辑推理、数学建模等综合能力,能有效提升学习能力和思维素养;《义务教育数学课程标准(2011年版)》要求:“数学模型思想寓于具体的概念、法则、现实问题解决以及一般数学问题的学习和探索之中.”随着问题逐渐深入,学生从不同的角度入手,分析思考问题,激活思维,领会数学模型的含义和作用,感受数学模型思想,体会数学的应用价值,树立数学的应用意识,积累解决问题的经验[3].
陶行知说过:“教师的职责不在教,而在于教学生学.”在“一题一课”的实施过程中,采取分步递增条件呈现原题,让一题变多题,并通过开放性问题涉及数学结论,促使学生主动、全面和深入学习,真正做到“做一题,会一类,通一片”,使得课堂教学更加高效,学生的数学核心素养得以培养和提升.
