基于烟叶物理属性的烟叶出片率模型研究

李新锋，徐小红

(福建省龙岩金叶复烤有限责任公司，龙岩 364102)

出片率是指烟叶原料经过打叶复烤后，成品片烟(含2.36 mm以上的碎片)质量占净投料质量的百分比[1]。出片率的高低能侧面反映出企业的加工水平，决定企业的经济效益。长期以来，对烤烟出片率的研究，侧重于烟叶物理属性与烟叶出片率的相关性研究[2，3]，或打叶工艺设备、工艺参数对出片率的影响[4～9]，很少根据烟叶物理属性建立出片率回归模型。本研究根据烟叶物理属性的各个指标，通过逐步回归、主成分回归、基于网格寻优法、遗传算法、粒子群算法寻找最优参数c、g的支持向量机回归方法建立回归模型，通过回归模型预测出片率，为在线工艺参数设定及技术经济指标合同的谈判和签订提供依据。

1 材料与方法

1.1 材料

2016～2017年共选取烟叶模块73个，采用随机分布抽样法选取58个模块样品作为训练集，15个模块样品作为验证集。

1.2 测定项目与方法

1.2.1 烟叶物理属性的测定

烟叶物理属性[10]测定包括原始含梗率(x1)、原始含水率(x2)、单叶重(x3)、长度(x4)、宽度(x5)、单位面积重量(x6)、叶片厚度(x7)、密度(x8)。

1.2.2 烟叶出片率的测定

烟叶出片率(y)的测定参考《打叶烟叶质量检验》[1]标准进行。

1.3 模型构建与验证

1.3.1 逐步回归法建模

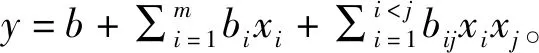
1.3.2 主成分回归法建模

主成分分析是将原来具有一定相关性的自变量，通过线性组合的方式重新组合成一组较少的线性无关的综合指标代替原来的指标，新变量能反映出原变量的绝大部分信息。主成分回归中第一主成分x1对应于数据变异(贡献率e1)最大的方向，对x2，x3，…xm依次有e2≥…≥em。主成分回归以m个新变量中的前k个贡献比较大的新变量作为自变量建立回归方程。

1.3.3 支持向量机回归法建模

支持向量机通过用内积函数定义的线性变换到一个高维空间，在这个空间中寻找最优回归超平面[11]，使样本数据到该平面的距离最小以实现回归。本研究希望通过寻找这样的超平面，找出自变量与因变量在高维空间中的定量关系[12～16]。

假设在出片率回归试验中共得到n组样本(X1，Y1)，(X2，Y2)…(Xi，Yi) …(Xn，Yn)，且每个Xi都是一个8维向量，可表示为

Xi=[xi1，xi2，xi3，xi4，xi5，xi6，xi7，xi8]’

(1)

式中：xi1，xi2，xi3，xi4，xi5，xi6，xi7，xi8分别表示为第i个样本中的原始含梗率、原始含水率、单叶重、长度、宽度、单位面积重量、叶片厚度、密度。

通过映射函数Φ(X)将Xi映射到高维的特征空间，建立线性回归模型来估计回归函数，公式如下：

f(X，w)=w×Φ(X)+b

(2)

式中：w为权向量，X为输入向量，b为阈值。

对于给定样本集，采用ε不敏感函数，对应的支持向量机为ε-支持向量机，其约束优化问题可表示为：

i=1，2…n

其中

(3)

式中：c是惩罚因子，本研究采用网格寻优法、遗传算法、粒子群算法找出最佳参数c。

式(3)的优化问题引入拉格朗日函数将其转化为对偶问题，通过解对偶问题得到式(2)的解：

(4)

令g=1/δ2，采用网格寻优法、遗传算法、粒子群算法找出最佳g参数。

任何烟叶物理属性组合对应的输入向量Xi通过式(4)都可以得到出片率预测结果，从而实现烟叶出片率的回归与预测分析。

1.4 模型评价方法

采用绝对系数R2、校正标准偏差SEC、预测标准偏差SEP作为模型精度的评价方法。对于建模集而言，R2越大，SEC越小，建模精度越高，模型越稳定；对于预测集而言，R2越大，预测标准偏差SEP越小，模型预测精度越高。

2 结果与分析

2.1 烟叶出片率与烟叶物理属性总体情况

由表1可知，烟叶出片率变幅为62.48%～73.85%，变幅较大；原始含梗率(x1)、原始含水率(x2)、长度(x4)、宽度(x5)变异系数较为稳定，而单叶重(x3)、单位面积重量(x6)、叶片厚度 (x7)、密度(x8)变异系数在12.38%～17.92%，较不稳定。叶片厚度(x7)标准偏差最小，密度(x8)标准偏差最大，其余指标标准偏差居于中间。

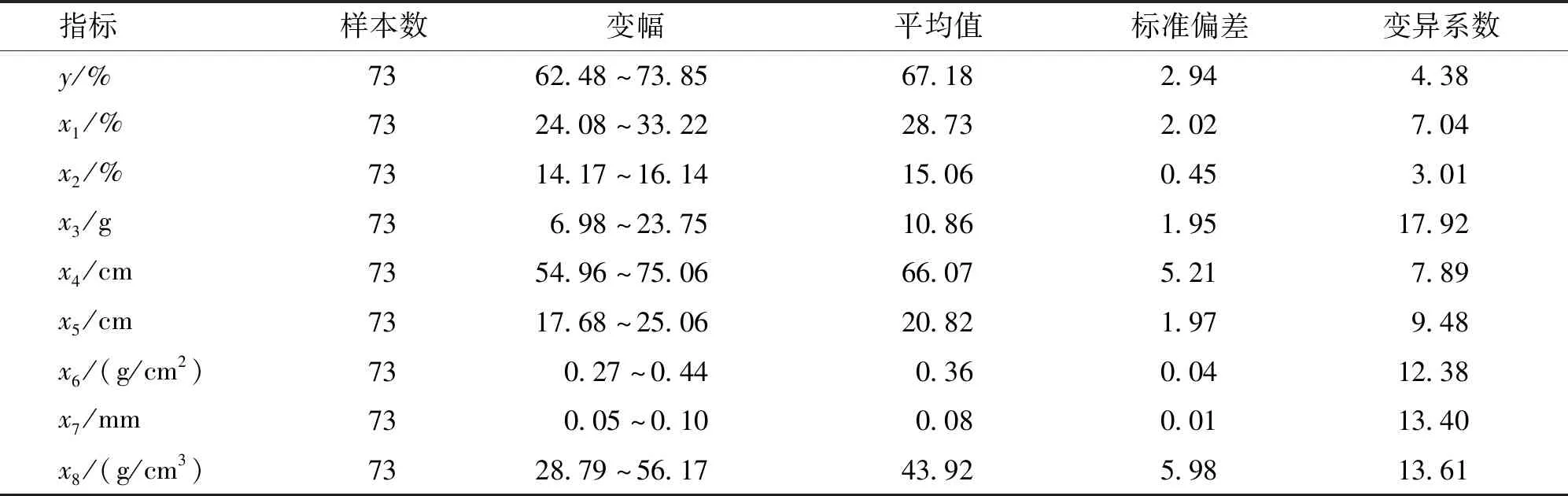
表1 烟叶出片率与烟叶物理属性的描述性统计

2.2 烟叶出片率预测模型的构建

2.2.1 逐步回归法建模

采用Matlab做逐步回归分析，结果如表2所示。建立包含含梗率(x1)、原始含水率(x2)、长度(x4)、叶片厚度 (x7)、密度(x8)等指标的估计出片率的最优回归方程：

y=199.270+4.582x1-17.874x2-3.654x4+1417.1x7+1.157x8-47.774x1x7-0.039x1x8+0.242x2x4。

对各偏回归系数显著性进行检验，结果显示：含梗率(x1)、原始含水率(x2)、长度(x4)、叶片厚度(x7)达到极显著水平(p<0.01)、密度(x8)达到显著水平(p<0.05)，对截距的检验结果为显著(p<0.05)，可以认为所得的逐步回归方程成立。采用F检验方法对构建的逐步回归方程进行显著性检验，检验结果显示达到极显著水平(F=47.400，p<0.01)，说明该方程具有统计学意义。

表2 逐步回归方程偏回归系数和回归常数显著性检验结果

2.2.2 主成分回归法建模

采用Matlab软件做主成分回归分析，提取前8个主成分(累积贡献率达到95.096%)参与建模，回归方程为：

y=104.029-0.426x1-1.378x2+0.045x3-0.149x4-0.157x5+12.232x6+59.578x7-0.014x8

2.2.3 支持向量机回归法建模

采用Matlab软件中的map min max函数进行数据的归一化，同时采用网格寻优法、遗传算法、粒子群优化法寻找最佳参数c和g，对比各参数下SVR的训练与回归结果(图1～3)。

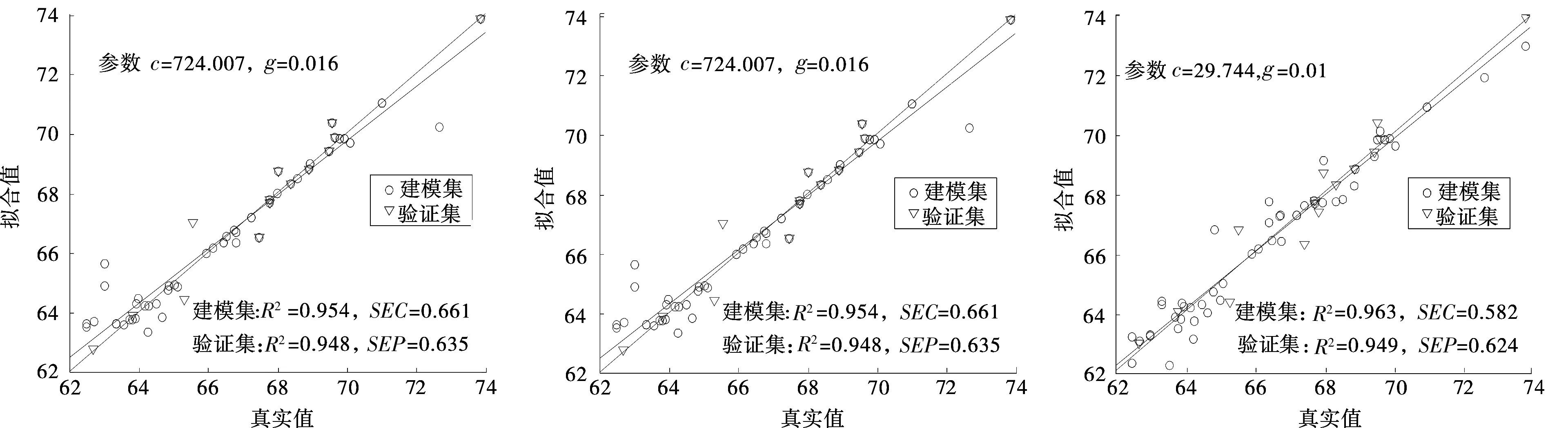
图1 网格寻优法 图2 遗传算法 图3 粒子群优化法

对比3种参数优化法，粒子群优化法建模集和验证集的决定系数R2均大于其他2种方法；同时，粒子群优化法建模集的校正标准偏差和验证集的预测标准偏差均小于其他2种方法；因此选择粒子群优化法确定最佳参数c=29.744，g=0.01。在此参数下进行SVR的训练与回归，结果如表3所示。训练过程中共迭代53次。回归过程中校正标准偏差和决定系数分别为0.582和0.963。

表3 支持向量机回归结果参数表

2.3 模型对比分析

对逐步回归、主成分回归、支持向量机回归3种方法构建的出片率模型进行比较，建模集采用决定系数和校正标准偏差(SEC)判定，验证集采用决定系数和预测标准偏差(SEP)判定，得出不同模型的建模和验证精度(表4、5)。可以看出：支持向量机建模集和验证集的决定系数(R2)比其他两种建模方法大，同时建模集的校正标准偏差(SEC)和验证集的预测标准偏差(SEP)比其他两种建模方法小，表明采用支持向量机方法建模和验证较其他两种建模方法好。

表4 不同模型建模的验证精度

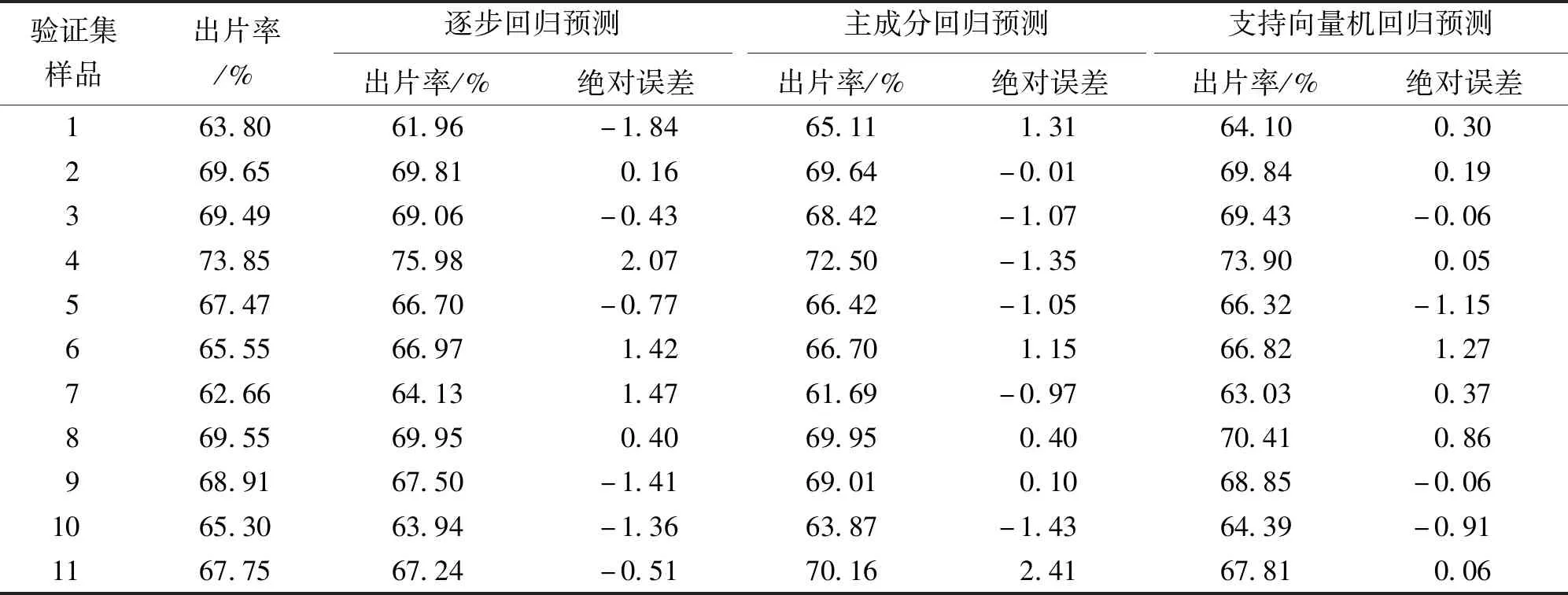
表5 不同模型预测结果对比

续表5

验证集样品出片率/%逐步回归预测主成分回归预测支持向量机回归预测出片率/%绝对误差出片率/%绝对误差出片率/%绝对误差1268.3867.84-0.5468.29-0.0968.33-0.051368.0268.200.1869.101.0868.710.691467.7668.180.4267.75-0.0167.71-0.051567.8866.69-1.1966.14-1.7467.44-0.44

3 小结与讨论

3.1 小结

(1)逐步回归分析结果显示，影响出片率的主要烟叶物理属性指标为含梗率、原始含水率、长度、叶片厚度、密度。

(2)网格寻优法、遗传算法、粒子群优化法均有良好的泛化能力，可以用于出片率预测，其中粒子群优化法出片率预测结果优于其他两种方法。

(3)逐步回归、主成分回归、支持向量机回归3种方法模型预测精度都较高，说明3种方法对出片率的预测是可行的。其中，对出片率预测最好的模型为粒子群优化法选择的最佳参数所对应的支持向量机回归模型，其次是逐步回归模型，预测能力最低的是主成分回归模型。

3.2 讨论

本研究从烟叶的物理属性分析烟叶出片率，如果将烟叶的物理属性与在线工艺参数结合在一起，更全面地分析烟叶的出片率，可能会有新的突破。