平抑算法对风电并网平滑度判据标准研究

王战栋，陈 洁

(新疆大学电气工程学院，新疆 乌鲁木齐 830047)

0 引 言

近些年来，能源资源消耗严重，且化石燃料所造成的环境污染对生态环境和自然环境造成不可磨灭且不可逆的影响。风力发电作为新一代的清洁能源，具有无污染，可再生等优点，因此日益受到世界各国的重视。截止2017年中国的风电装机容量已经达到1.95 GW[1]，由于大规模的风力发电并入电网，风力发电出力的随机性、波动性等问题。因此为解决这一问题，各国专家研究通过装配储能系统用于平滑风力发电的有功功率曲线平抑风电的有功功率波动，提高风电的并网质量，减少风力发电的弃风限电现象。

储能系统对风力发电的有功功率波动平抑算法主要有：

(1)一阶低通滤波算法，其将风电场有功功率出力数据经过由两个时间常数控制的一阶低通滤波器平抑后，得到高频与低频的有功功率平抑信号，由低通滤波器特性可知时间常数越大，有功功率出力平抑效果越好。文献[2]采用两个一阶低通滤波器来平滑风电输出的波动，并建立了反映混合储能参数的长期数学模型。

(2)小波滤波算法，由于是自适应滤波算法，对风电出力这种波动不平稳信号处理具有很大的优势。文献[3]利用小波滤波算法对风电有功功率的高频信号和低频信号进行提取，分别使用超级电容器与蓄电池进行平抑。

(3)模型预测控制算法，文献[4]提出一种双层控制模型，并建立专家信息库。由风电功率和储能的荷电状态依次检索专家信息库，得到相应的控制算法控制储能系统充放电，平抑风电功率波动。

这3种算法在风电输出功率波动性平抑上有着各自的优缺点，但却没有进行相应的对比与分析，且文献中大多没有对平抑算法在平滑风电功率波动后满足国家电网并网标准进行定量的分析。

1 一阶低通滤波算法

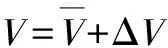
(1)

由式(1)的风速分解结果可得

PW=Pave+Pvar

(2)

式中，PW是风力机的实时输出功率；PW可以分解为平均风速产生的功率Pave和瞬时风速产生的功率Pvar。一阶低通滤波器可以过滤掉风电出力的高频部分，使风力发电场能够获得相对平滑的风功率并入电网[6]。由PW产生的平均风速分量Pave一阶低通滤波关系为

(3)

为了评价一阶低通滤波器对有功功率的平滑效果，满足国网1 min和10 min的并网标准，令Δt=1 min，在一天24 h将其分为24×60个分断点，设定采样点为1 440个点，则每个采样分段点的波动率Δδi为

(4)

式中，Pave(i)为第i分钟连接到电网的功率；Q是发电场的装机容量。如果发电系统1 min的限定功率变化量为Δδ，则第i分钟波动率的特征量L(i)可定义为

(5)

因此表示有功功率输出平滑性的函数LOS表示为

(6)

根据风电场并网技术规范，给出了风电场最大功率波动的推荐值。在1 min内，最大功率波动率通常低于装机容量的5%，而γ是1 min内的最大功率波动率[6]。根据新疆某装机容量为50 MW风电场数据分析得出：风电场装机容量小于5%的概率分布与一阶低通滤波器时间常数的关系如图1所示。

图1 最大功率波动率小于风电场装机容量5%的概率分布

当t1小于10 min时，在5%的装机容量以下1 min 内最大功率输出变化率变化的概率增长缓慢。当t1=10 min时，最大功率变化率在1 min内达到装机容量的5%以上，达到100%。因此，时间常数t1的取值范围需要10 min。1 min下满足风电场并网标准，最大功率变化率在装机容量的5%以下，10 min时最大功率变化率在装机容量的15%以下，计算过程如上所示相同。

2 小波滤波算法

2.1 小波滤波算法简述

小波滤波算法是小波技术的一种重要应用，小波变换的窗口面积固定，函数的形状随时可以改变的时域局部化信号的一种分析方法，其时频局部化和多分辨率性质使得小波滤波可以在滤除高频噪声的同时保留信号的突起和边缘。利用小波变换对风电瞬时功率中的高频干扰部分进行滤除，从而保留功率阶跃的高频部分[7]。从实际应用来看，超级电容器平滑有功功率波动高频部分，电池跟踪功率的阶跃信号以减少延迟。原始信号S经过小波分解得到低频信号A1和高频信号D1，对上层得到低频信号A1再次通过小波分解得到低频信号A2和高频信号D2，则低频信号A3和高频信号D3可对A2进行小波分解得到。因此三层小波分解树变换图如图2所示。

图2 三层小波分解树变换示意

由上图知小波变换只是每一层对上一层分解的低频信号进行小波变换，没有对每一层分解的高频信号进行小波变换，从而导致对局部高频信号的时频域分析产生问题。因此小波包变换随之而生，其在小波变换的基础上对每一层分解的高频信号再次进行分解，分解程度更加精细。小波包数学定义为

(7)

式中，{hk}k∈z是低通滤波器的系数；{gk}k∈z是高通滤波器系数；μ0(t)、μ1(t)为正交尺度函数。μ0(t)、μ1(t)、hn、gn定义小波包函数为

(8)

则小波包分解算法可表示为

(9)

小波包重构算法为

(10)

如图3所示可以看出小波包分解对每一层的高频信号进行了分解，H和L分别是信号进行小波包分解后的高频信号和低频信号。N层信号进行分解可以得到2n个信号。

图3 三层小波包分解树结构示意

利用储能系统对风电场输出有功功率进行平抑，对风电输出功率进行小波包分解，得到风电有功功率并网目标曲线、能量密度型储能平滑风电输出功率的低频波动目标曲线和功率型储能平滑风电输出功率的高频波动目标曲线。

通常对风电有功出力进行小波包分解时，分解层数越多，则得到的并网目标功率曲线越平滑，储能系统对风电场输出有功平抑效果越好。但不同的小波包分解层数得到的有功功率目标曲线不一定能够满足国家电网并网的技术标准，经过n层小波包分解，第一次出现的满足国网并网技术标准的低频信号作为小波包分解最佳层[8]。对风电有功功率信号较大层数的小波包分解更能满足国网并网技术标准，使并网功率目标曲线更平滑，提高风电并网质量，但相应的需要的储能装置将增多，不符合经济性要求。

2.2 小波包最佳层数分析

风电场有功功率信号经过小波包分解，得到低频功率信号、中频功率信号、高频功率信号，其中低频功率信号幅值与风电场并网目标功率信号相似，则低频功率信号可以直接并入电网，而中频功率信号可以由能量密度大、功率密度小且充放电时间长的储能来平抑，高频功率信号可以由功率密度大、可以频繁充放电的储能来平抑[9]。风电功率分解层数越多，并网目标功率曲线就越平滑，但储能设备的增多加大了风电场的投资，不利于可再生能源风力发电的建设。

风电历史有功功率出力曲线经过5层小波包分解得到1 min和10 min功率波动量如图4、5所示。

图4 5层小波包分解10 min波动量与时间t关系

图5 5层小波包分解1 min波动量与时间t关系

《风电场接入电力系统技术规定》中对风电场接入电力系统的有功功率最大功率变化率推荐值如下：风电场装机容量为30～150 MW时，风电场10 min最大功率变化量和1 min最大功率变化量分别为装机容量/1.5(3) MW和装机容量/5(10) MW。

对图中5层小波包分解风电有功功率得到1 min和10 min的输出目标功率波动量曲线知，分解层数为5层时，1 min和10 min的最大功率变化量均能满足国家《风电场接入电力系统技术规定》，虽然能够继续增大分解层数且能使风电场1 min和10 min最大功率变化量更少，使有功功率输出目标功率曲线更加平滑，更能满足接入电力系统技术规定，但分解层数的增大必然使储能设备增多，加大投资，使整个系统的经济性变差，不利于风电的大规模建设与发展[5-9]。因此将小波包分解层数n=5作为平抑风电场有功功率的最佳分解层数。

3 模型预测控制

3.1 模型预测控制算法简述

模型预测控制是基于过程预测模型的一种方法，是一种使用回退视界且在线考虑系统约束条件的控制方法，具有安全约束和方便处理系统设备的特点，在风电领域得到了广泛应用[10]。由于模型预测控制算法具有良好的约束处理能力，将风电输出目标有功功率波动率作为安全约束条件，提出基于风电并网波动率的模型预测控制算法。将一天的控制时间段中1 min的有功功率波动率最小作为优化目标，对于有功功率波动率的一阶低通滤波器和模型预测控制算法比较分析。

考虑到风电场有功功率并入电力系统的稳定性与经济性，设定1 min和10 min的时间段中的平抑波动率指标，一天中任意1 min内有功功率目标最大值与最小值之差小于y1(1 min最大功率变化量)

3.2 控制系统模型分析

风电功率PW和储能系统输出功率PB合成P0经过升压变压器并入电网，储能系统控制器实时监控风电功率PW，综合平抑功率波动指标向储能系统双向变流器释放充放电功率指令。则

P0(k+1)=PW(k)+PB(k)

(11)

式中，PW(k)为k时刻风电有功功率;PB(k)为k时刻储能系统输出功率;P0(k+1)为k+1时刻风电并网功率。

储能系统在k时刻的储存能量EB(k)如式(12)

(12)

式中，EB(0)为储能系统在0时刻的储存能量;PB(j)为储能系统在第j时刻的输出功率。

有功功率波动功率1 min和10 min约束条件如下

(13)

(14)

(15)

(16)

(17)

风电场额定容量Prated为50 MW，选取1 d内24 h的风电输出功率历史数据，在1 d内任意1 min的经过算法平抑风电功率曲线如图6所示。

图6 任意1 min最大波动量与时间t关系

原始风电功率波动较为剧烈，经过算法平抑之后任意1 min的波动率显然低于2 MW，任意10 min的波动率计算与上面相同不做赘述。通过计算知1 min和10 min的功率波动率都低于国家对风电场的并网技术要求，满足《风电场接入电力系统技术规范》。

4 三种平抑算法的结果分析

通过应用上述3种平抑算法得到1 min和10 min的功率波动数据结果表明：模型预测控制算法在对风电进行平抑得到的功率波动数据更低，更加符合并网标准，且采用一阶低通滤波算法对风电有功功率进行平抑，计算得到储能系统的最大功率和容量分别为11.120 8 MW和21 264 kW·h。应用小波滤波算法对风电有功功率进行平抑，计算得到储能系统的最大功率和容量分别为10.783 9 MW和163 761 kW·h。采用模型预测控制算法对风电有功功率进行平抑，计算得到储能系统的最大功率和容量分别为10.276 3 MW和12 674.9 kW·h。由配置储能系统的最大功率及容量结果可知，模型预测控制算法平抑得到储能系统最大功率更小，容量配置结果最低，则储能出力更加平滑，对储能容量需求较小，大大节省了成本，经济性更优。

5 结 论

本文对提出的3种主要常用平抑风电功率波动的算法：一阶低通滤波算法、小波滤波算法、模型预测算法分别进行分析，这3种平抑算法均能够平抑风电有功功率波动，使风电目标有功功率满足并网技术要求。对其进行定性定量的计算分析可知，模型预测控制算法在平滑风电输出功率中，功率波动数据和储能系统最大功率及容量最低，提高系统的经济性。模型预测控制算法对以用储能系统平抑风电功率波动有较好的指导意义。