闸室抗滑稳定的模糊随机可靠度分析

陶永霞，秦净净，于 洋

(黄河水利职业技术学院，河南 开封 475000)

闸室是水闸的主体结构，其安全性直接关系到整个水闸工程的安全稳定[1]。全国病险水闸除险加固专项规划调查表明，全国共有大型水闸486座，中型水闸3 278座，小型水闸4.6万多座，其中大中型病险水闸1 782座，包括大型水闸260座，中型水闸1 522座[2]。在对各类节制闸进行病害评估的过程中发现，水闸失事的主要原因是材料强度难以控制，土工参数选取误差较大，并且闸室稳定和失稳之间存在着一个模糊过渡区[3]。因此对于节制闸稳定性的分析，应当综合考虑其随机性和模糊性的特点。

随着我国GB 50199—2013《水利水电工程结构可靠度设计统一标准》的颁布实施[4]，闸室抗滑稳定计算方法也正由单一的安全系数转变为基于可靠度理论的极限状态。针对闸室传统抗滑可靠度上，很多学者已经作了一些相关性研究工作，并取得了一定成就。齐艳杰等[5]利用蒙特卡罗法等对水闸闸室进行稳定分析，并研究不同变量的均值、变异系数、分布类型对其可靠度指标的不同影响；王成[6]利用ANSYS软件的PDS模块，结合蒙特卡罗法与随机有限元法对闸墙结构进行可靠性分析；刘庆晶等[7]利用模糊点估计法对水闸渗流可靠度进行探讨。纵观有关节制闸可靠性评估研究工作可以发现考虑工程参数的模糊性以及失效准则模糊性所引起的结构失效概率计算结果的变化深入研究的不多。

模糊随机可靠度理论考虑了地基参数的模糊性和随机性，已在边坡可靠度分析中得到应用，而此方法在水闸工作中应用较少[8-9]。鉴于此，本文对水闸闸室抗滑稳定可靠度分析中涉及的土体的摩擦系数和粘聚力等几个主要随机变量的统计特征进行分析研究，模糊随机变量采用模糊截集，将闸室失稳状态和稳定状态之间的界限采用隶属度函数模糊化，对某闸室抗滑稳定可靠性进行探讨，得到相应的模糊随机可靠度指标和失效概率，与传统可靠度理论方法比较，并分析随机模糊参数水平截集、负相关性、隶属函数取值界限以及隶属函数形式对模糊可靠度指标的影响，计算结果具有一定的工程应用价值。

1 闸室抗滑稳定性模糊可靠度

1.1 参数的模糊截集处理

土质参数服从正态分布，其模糊性可用拟正态分布隶属函数进行描述[10]，即

(1)

式中，μx为变量x的均值；σx为变量的x的方差；k为模糊隶属函数的取值界限，取值范围0.5～3.0[11]。

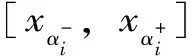
(2)

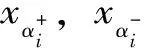
(3)

式中，Zj为截集αi上第j种组合对应的功能函数值；Pj为该参数组合的权重系数；ρrt为模糊随机变量xr和xt的相关系数。取xr在αi水平截集上区间右端点时，er=1，否则er=-1，et规定同er。

利用普通加权平均法得到功能函数Z的总均值和总方差μ(Z)和方差σ2(Z)，即

(4)

1.2 失效准则界限模糊的隶属函数

实际工程中的节制闸闸室稳定与否不存在严格的界限，即不能简单地用储备函数Z>0，Z=0，Z<0来判别闸室抗滑的稳定状态。根据模糊概率理论，99.73%的数据落在(μ-3σ，μ+3σ)区间内，因此，本文功能函数失效准则不清晰的隶属函数采用岭形分布中的偏小型分布函数，形式为

(5)

式中，σZ为Z的标准差，该隶属函数的图像如图1所示。

图1 偏小型岭形分布隶属函数

2 工程实例

某开敞式节制闸，总长101 m，5孔，每孔净宽4 m，闸孔总净宽20 m。中间3孔一联，两侧各一孔一联，中墩厚1.0 m，边墩厚0.7 m，缝墩厚1.42 m。闸底板高程57.40 m，底板厚1.0 m，上下游端各设置一个深0.7 m的浅齿墙，闸室顺水流方向长12 m。闸墩顶部高程62.00 m，长12 m。闸墩以上设置排架，排架高5.1 m，排架上设置梁式工作桥，工作桥上设置砖混结构启闭机房，闸室两岸设置砖混结构桥头堡。闸室下游侧设置交通桥，为钢筋混凝土预制板桥，桥面净宽4.5 m，总宽5.0 m。结构形式为钢筋混凝土板式结构，剖面如图2所示。

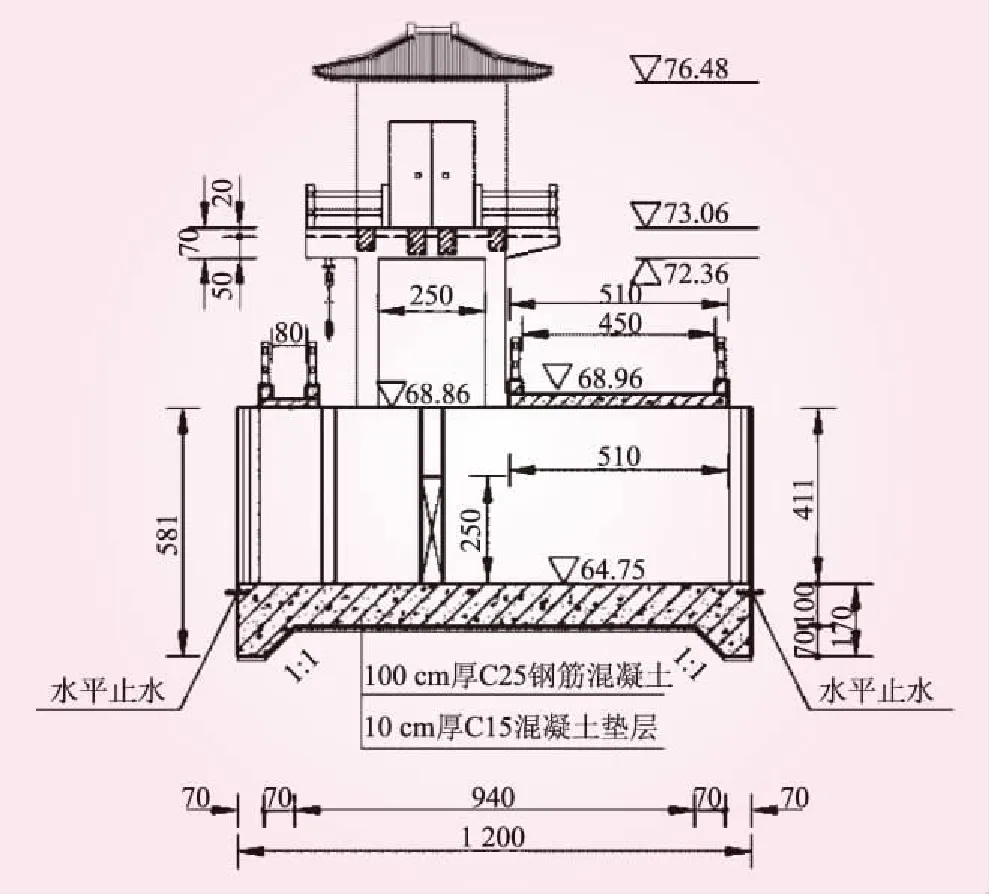
图2 闸室剖面(尺寸单位：cm)

根据地质勘探报告，闸底板高程为56.40 m，位于中粉质壤土内，土质参数服从正态分布，闸下土基的参数见表1。

表1 节制闸闸室随机变量特性

注：粘聚力和摩擦系数均服从正态分布．

2.1 模糊随机可靠度分析

对该水闸闸室的挡水工况(正常蓄水期上游水位为59.82 m，下游无水)进行抗滑可靠度分析，考虑到实际土质力学参数的最大可能取值区间，取模糊取值边界k=3，即用μ±3σ表征拟正态隶属函数取值界限，为了尽可能地减小计算结果的离散性，采用9个水平截集，即αi=0.1～0.9，对不同水平截集加权得到总均值和总方差，然后根据失效准则隶属函数求解水闸闸室抗滑稳定模糊随机可靠度为3.107，根据自适应重要抽样MC[12]计算结果为2.998，误差为3.634%，因此本文的计算方法是可行的。为了便于和以往的可靠度指标相对比，本文增加传统可靠度和不考虑稳定系数隶属函数以及不考虑参数模糊性情况下的可靠度指标计算，各方法的结果对比如表2所示。

表2 各方法可靠度指标计算结果对比

从表2可以看出，模糊随机可靠度的失效概率偏小，传统的节制闸可靠性分析方法由于没有考虑随机变量和失效准则模糊性对失稳概率的影响，得出的可靠指标过小，过大地估计了节制闸的稳定可靠状态。因此，模糊随机得出的破坏概率结果更符合工程实际，有利于决策者判断闸室的安全状态，具有一定的工程应用价值。

2.2 参数负相关性对可靠度影响

考虑抗剪断参数f和c的负相关性对可靠性计算结果的影响，当k=3时，取不同的相关系数进行模糊可靠性计算，计算结果见表3。

表3 参数相关性对计算结果的影响

从表3可以看出，土基抗剪断参数f和c从独立到完全负相关，模糊可靠度指标由3.107增加至3.213，增加率为3.411%。因此，参数的负相关性对闸室抗滑模糊随机可靠性指标的影响并不大，随负相关系数绝对值的增大，可靠性指标稍有增大，可以忽略不计。

2.3 模糊隶属函数取值界限表征参数对可靠度影响

模糊隶属函数取值界限表征参数k的取值大小受参数变异性、样本数大小等影响在 0.5～3.0 范围内选取[11]。为了研究k对闸室抗滑可靠度影响，本文取k=0.5，1.0，1.5，2.0，2.5，3.0，计算结果如图3所示。

图3 模糊变量不同取值界限对应的可靠指标

从图3可以看出，水闸抗滑稳定模糊随机可靠度随着取值边界的增大而减小，这是由于取值界限k越大，抗剪断参数f和c的置信度越低，导致模糊随机可靠度指标值越小。因此，当参数变异性越大，为安全考虑建议k取值为3。

2.4 失效准则隶属函数构造对可靠度影响

隶属函数的构造在模糊分析中的作用至关重要，模糊随机可靠性分析评价的合理性很大程度上取决于失效准则隶属函数确定的正确性，其形式主要为半梯形分布、岭形分布等。为考虑隶属函数的形式对计算结果的影响，本文失效准则隶属函数分别选取降半岭型和降半梯型和分布函数，半梯型分布函数形式为

(6)

两种形式的模糊可靠度随模糊隶属函数取值界限表征参数k变化趋势如图4所示。

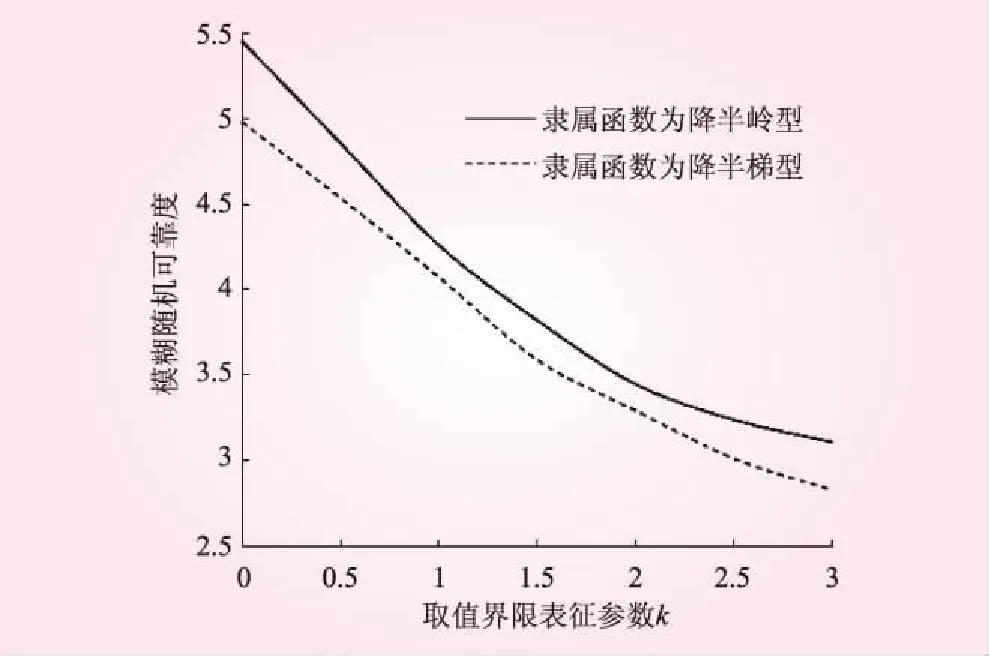
图4 不同失效准隶属函数在模糊变量不同取值界限对应的可靠指标

从图4可以看出，失效准则选取降半岭型和降半梯型分布函数，模糊随机可靠度指标均随模糊变量隶属函数取值界限的增大而减小，失效准则隶属函数为降半梯型的模糊随机可靠度指标均比失效准则隶属函数为降半岭型大，因此，隶属函数的选取很重要，应结合模糊统计实验和专家经验选取。

3 结 论

本文以某节制闸为研究对象，以Matlab为分析平台，考虑闸基土质抗剪断参数f、c的模糊随机性以及闸室失稳失效准则模糊性，采用模糊随机理论对该闸基抗滑稳定性进行计算和分析，得到以下结论：

(1)传统可靠度的失效概率比模糊可靠度的失效概率小，因其没有考虑模糊随机可靠度考虑随机变量和失效准则模糊性对失稳概率的影响，没有使工程信息尽可能多地反映出来，得出的可靠度指标过大地估计了闸室的稳定可靠状态，故模糊可靠度算出来的结果更加符合实际。

(2)模糊变量的隶属函数取值界限越大，参数的不确定性越大，导致模糊可靠度指标值越小。因此，为安全考虑当参数变异性比较大时，建议k取3。

(3)土基抗剪断参数f和c随负相关系数绝对值的增大，模糊随机可靠性指标稍有增大，可以忽略不计。

(4)失效准则隶属函数为降半梯型的模糊随机可靠度指标均比失效准则隶属函数为降半岭型的结果大，失效准则的隶属函数选取很重要，然而隶属函数的准确确定不太现实，闸室稳定隶属函数表达式仍然包含很多人为因素，应结合模糊统计实验和专家经验选取，同时需要工程实例的检验和修正。