基于改进的最优分割法的不同论域对汛期分期影响研究

许钰沐，牛秀岭

(1.山西冶金岩土工程勘察有限公司，山西 太原 030024；2.山西水务交口供水开发建设管理有限公司，山西 太原 030024)

0 引 言

科学合理的汛期分期对于流域的防洪减灾及水资源合理利用与保护具有十分重要的意义[1]。不同年份降雨量在不同时间段变化较大，汛期在不同年份都具有随机性、模糊性等变化规律[2]。目前，针对这些特点，现行的分期方法中仅Fisher分割法既能处理多指标的聚类问题，又能同时考虑样本时序性，在汛期分期中应用广泛[3-4]。但Fisher分割法在处理多指标聚类问题时缺乏对指标权重的考虑，即便唐莉等人将主成分分析法(PCA，principal component analysis)[5]与Fisher最优分割法结合，称之为PCA-Fisher最优分割，对水库进行汛期分期，克服了Fisher最优分割法视各指标等权重的不足[5]，但以往人们在运用Fisher分割法汛期分期时，存在人为确定汛期研究域与汛期分期的研究论域的问题，对于汛期的界定及汛期分期基本时间单元的选取都带有强烈的主观性与不确定性[6-7]。为此，本文以张家庄水库为例，首先定量确定汛期研究域，再分别以旬与候为研究论域，采用PCA-Fisher最优分割法，对水库进行汛期分期。

1 方法理论

1.1 Fisher最优分割法

Fisher最优分割法是将样本分成若干类，对一列有序样本进行分割，其分割原则是各类间的差异最大，各类内部的差异最小。具体分割步骤如下：

(1)样本数据处理。设n个有序样本，各有m项评价指标，xij即为第i个样本的第j个指标特征值，构造指标特征值矩阵X，对各指标无量纲化，得标准矩阵X′。即

xij′=xij/xmaxj

(1)

式中，xmaxj为第j个指标中的最大值，xij′是无量纲化后的值。

(2)定义类直径。设某类Gij={yi,yi+1,…,yj}j>i)的样本离差平方和为其直径D(i，j)V，即

(2)

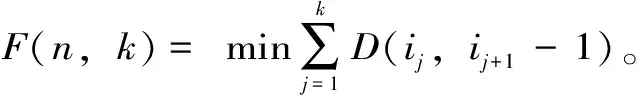
(4)最优解的确定。Fisher最优分割法具有如下递推定理

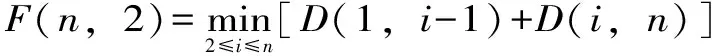
(3)

(4)

当分k类时，找ik分割点使得式(4)的值最小，即F(n，k)=F(ik-1，k-1)+D(ik，n)；从而求出第k类。然后再求ik-1分割点，使F(ik-1，k-1)=F(ik-1-1，k-2)+D(ik-1，n)，以此类推得出所有分割点求出最优解。

(5)最优分类数的确定。F(n，k)～k曲线的转折处的k值即为最优分类数；或当β(k)较大时则表示分k类较优,β(k)=|F(n,k)-F(n,k-1)|,一般以β(k)最大值时对应k值为最优分类数目。

1.2 均值变点分析

王贺佳等提出可以采用均值变点分析将寻找非汛期与汛期转化为寻找降雨-径流相关系数强度的变点[6]。均值变点分析的步骤如下：

对于有序相关系数数列{λθ}(θ=1，2，…，12)，以λt为端点将{λθ}划分为两列：λ1，λ2，…，λt和λt，λt+1，…，λ12，其中λt=max(λ1，λ2，…，λ12)。

假定{λθ}在第θ个月与第θ+1个月处断开，则可计算统计量Dt和D，即

(5)

(6)

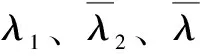
β=D-Dt

(7)

式中，最大β对应的第θ个月为变点，从而可以求出汛期开始的月。

同理，对有序数列λt，λt+1，…，λ12进行上述演算，也就可以得到汛期结束的月。根据汛期开始与结束的月，可以对汛期与非汛期进行划分。

2 实例分析

张家庄水库位于山西省孝义市城西2.5 km的孝河上，是一座综合利用的中型水库，兼有防洪、农业灌溉、生态供水等综合效益。

2.1 研究期确定

本文以张家庄水库1994年～2014年共21 a的月降雨-径流资料为基础，得到了月降雨P和径流R的平均相关系数矩阵X=[0.02 0.24 0.22 0.39 0.64 0.72 0.73 0.67 0.75 0.50 0.29 0.01]T，可得最大相关系数为0.75；以0.75为端点，可将月降雨P和径流R的平均相关系数矩阵划分两列，即1月到9月和9月到12月两列，分别使用式(5)～(7)对两列相关系数矩阵计算β。结果见图1及图2。由图1、2可知，第1变点为第4个月，第2个变点为10月，即4月到10月为张家庄水库汛期。

图1 β随 θ变化第1变点

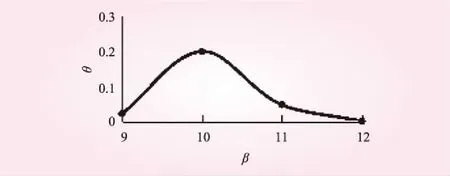
图2 β随 θ变化第2变点

2.2 基于旬的汛期分期

2.2.1样本指标选取及指标权重计算

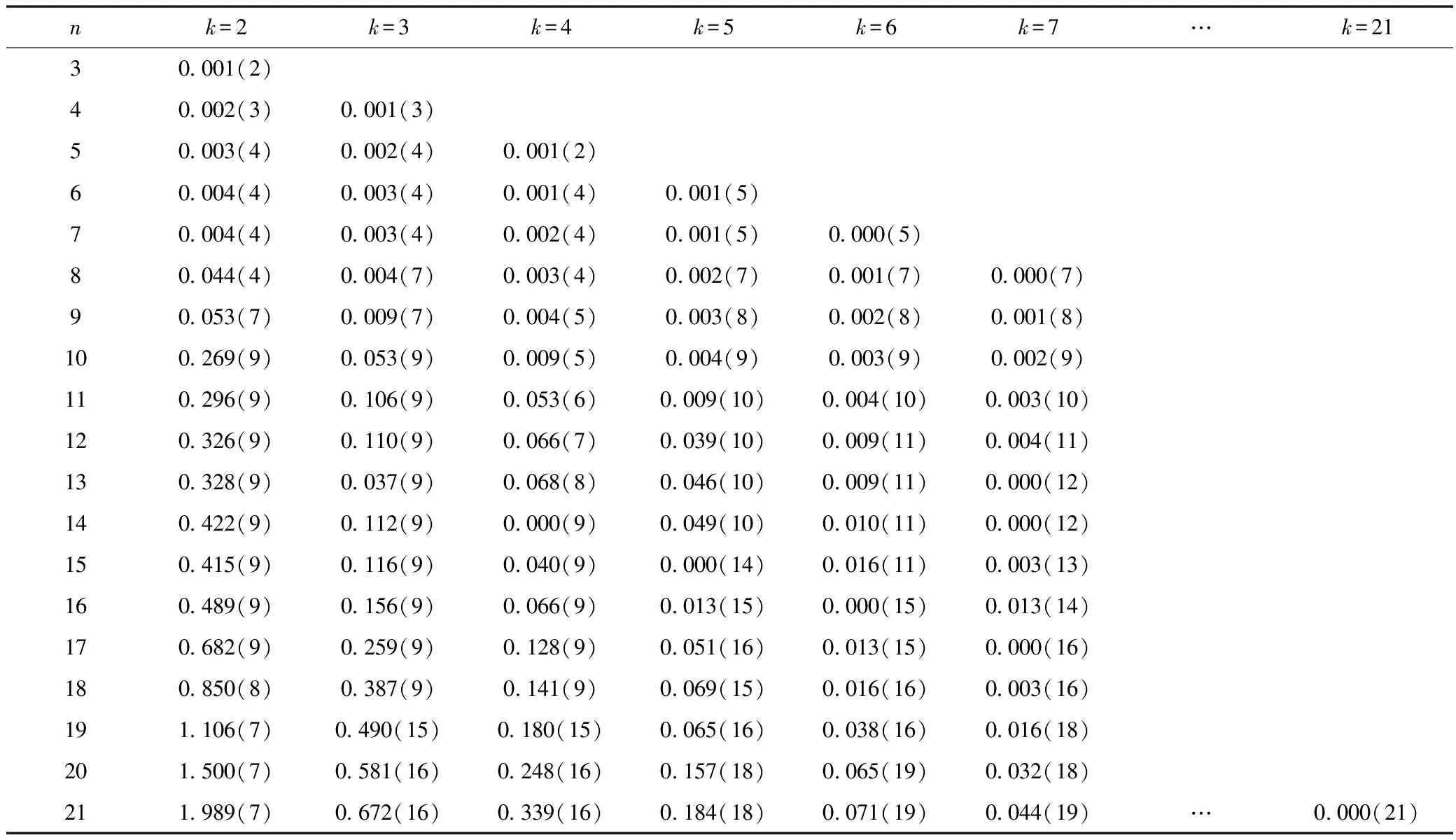
表3 以旬为基本单元的F(n,k)计算结果

以4月～10月为汛期研究域，可将整个汛期研究时段划分为21个旬。以张家庄水库1962年～2014年共53 a的逐日降雨资料为基础，选取表1中能反映张家庄水库流域范围内暴雨洪水特征的4个指标作为研究对象。运用SPSS软件对标准化的样本数据进行主成分分析[8]，可得表1及表2。

表1 成分矩阵(成分1)

表2 解释的总方差 %

由表2可知，主成分1特征累积方差贡献率≥80%。因此，其能够反映各指标的大部分信息。

各指标的权重ω=(0.745，0.188，0.035，0.032)。

2.2.2分期计算

由于各指标间的单位不同，首先要将各指标进行无量纲化处理。再利用上面求得各指标的权重系数，对无量纲化的结果求加权平均值。最后计算得出初始分类样本Y=[0.18 0.22 0.26 0.21 0.35 0.40 0.38 0.61 0.71 1.27 0.94 1.18 1.17 1.16 1.08 0.92 0.76 0.68 0.54 0.36 0.25]T；再计算各截断样本的目标函数F(n，k)值，计算结果见表3。

绘制目标函数F(n，k)～k、β(k)～k曲线如图3所示。从图3可以看出，在k=3处F(n，k)～k曲线最陡并出现拐弯，且β(k)～k曲线，k=3时，取值最大。所以可确最优定分类数k=3。从表4可以得出{1，2，3，4，5，6，7，8}、{9，10，11，12，13，14}和{15，16，17，18}3类。即，4月1日到6月20日为前汛期，6月21日到8月20日为主汛期，8月21日到10月30日为后汛期。

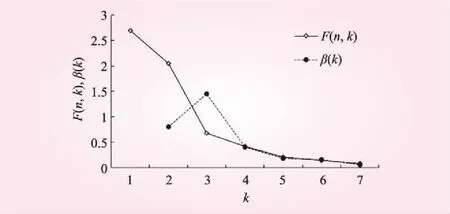
图3 以旬为论域的F(n，k)～k和 β(k)～k曲线

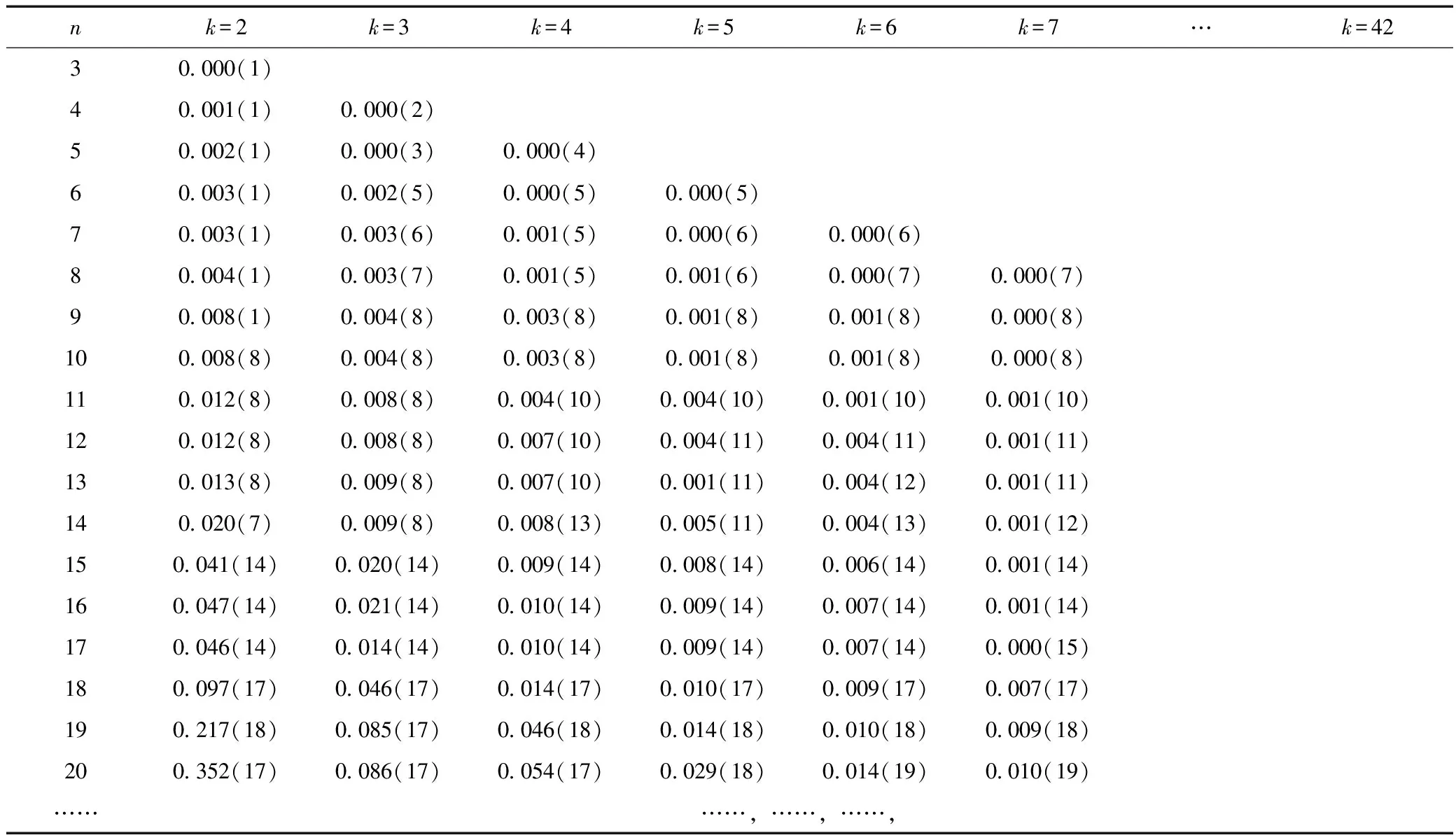
表4 以候为基本单元的F(n，k)计算结果

2.3 基于候的汛期分期

2.3.1样本指标选取及指标权重计算

以4月～10月为汛期研究域，可将整个研究时段划分为42个候。资料指标选取同上。运用SPSS软件对标准化的样本数据进行主成分分析[9]，得到各指标的权重ω=(ω1，ω2，ω3，ω4)=(0.865，0.073， 0.056， 0.005)。

2.3.2分期计算

以候为论域，对各样本指标无量纲化后，得出初始分类样本向量为：Y=[0.10 0.16 0.16 0.19 0.21 0.14 0.18 0.15 0.24 0.23 0.31 0.23 0.28 0.23 0.38 0.33 0.34 0.58 0.86 0.69 0.52 0.59 0.52 1.00 0.90 0.43 0.84 0.50 0.54 0.76 0.53 0.52 0.41 0.47 0.39 0.51 0.33 0.31 0.28 0.18 0.20 0.14]T。

再计算各截断样本的目标函数F(n，k)值，计算结果见表4。

图4 以候为论域的F(n，k)～k和 β(k)～k曲线

绘制目标函数F(n，k)～k、β(k)～k曲线(见图4)。由表4可得{1～17}、{18～29}和{30～42}3类，即4月1日到6月15日为前汛期，6月16日到8月31日为主汛期，9月1日到10月30日为后汛期。

3 结果与分析

张家庄水库现行的汛期研究域为6月～9月，而采用均值变点得到张家庄水库汛期研究域为4月～10月。其中，4月、5月和10月虽然不是北方地区公认的入汛期；但张家庄的降雨数据显示，4月份降雨总量于1994年首次超过7月，1994年后4月份降水总量频繁偏大。在1963年与1980年5月降水总量为全年最大值，其余年内有时5月比6月的降雨量还要多。研究期内多年10月与9月的降雨量相当，因此考虑气候变化和极端天气这两个因素，将4月、5月和10月划分到汛期里是合理的。

以旬与候为基本的研究论域分别对张家庄主汛期进行划分，得到主汛期时间段差异较大，以候为基本的时间单元，得到张家庄水库主汛期较以旬为基本时间单元长15 d，表现为主汛期提前到来且推后结束。究其原因，以候为基本的时间单元，汛期分期更为精细，样本间差异更为微小。在采用PCA-Fisher最优分割法进行汛期分期时，主汛期的时间跨度会变大，实际中主汛期变长有助于流域的防洪减灾，更有利于保障下游城镇居民的安全。因此，在进行流域汛期分期时，需要对比不同研究论域的汛期分期结果，尽可能地进行科学合理的汛期分期，以保障下游人民生产及生活安全。

4 结论与建议

(1)采用PCA-Fisher最优分割法可考虑各类指标权重，有效进行汛期分期。

(2)4月、5月和10月虽然不是北方地区公认的入汛期，但采用均值变点分析将4月、5月和10月纳入张家庄水库汛期合理。在不同流域对于汛期研究域的确定需要客观的分析降雨-径流的相关性，充分考虑气候变化和极端天气这两个因素。

(3)以旬与候为基本的研究论域分别对张家庄主汛期进行划分，得到主汛期时间段差异较大，研究论域越小，样本间差异更为微小，汛期分期更为精细。在进行流域汛期分期时，需要对比不同研究论域的汛期分期结果，尽可能的科学合理的进行汛期分期。