Tunable Weyl fermions and Fermi arcs in magnetized topological crystalline insulators∗

Junwei Liu(刘军伟) Chen Fang(方辰),and Liang Fu(傅亮)

1.Introduction

Weyl semimetals have doubly degenerate band crossings at isolated points(Weyl points)in Brillouin zone(BZ),with linear energy-momentum relation at low energy similar to Weyl fermions in high-energy physics.[1]These Weyl points in the band structure are the source or sink of Berry curvature in momentum space,and their presence gives rise to exotic phenomena such as topological Fermi arcs on the surfaces,[2]the chiral anomaly[3–5]and unusual quantum oscillations,[6]thus attracting tremendous interest.[7]

Weyl semimetals can be realized in two classes of materials,with broken inversion or time-reversal symmetry respectively.[8]Recently,the inversion-breaking Weyl semimetal phase has been predicted and observed in the TaAs class of materials,[9–15]and similar Weyl points have been found in photonic crystals.[16–18]On the other hand,although long sought after.[2,19–28]a time-reversal-breaking Weyl semimetal phase has yet be definitively found in real materials.The challenge is to find strong exchange coupling between magnetic order and itinerant electrons in a low(ideally zero)carrier density system.Among other things,magnetic Weyl semimetals are predicted to exhibit a unique anomalous Hall effect resulting from a nonzero net Berry curvature in momentum space,[29]and very large simultaneous anomalous Hall conductivity and the anomalous Hall angle have been observed in a very promising magnetic Weyl semimetal candidate Co3Sn2S2very recently.[30,31]

The recently discovered Sn1−xPbx(Te,Se)class of topological crystalline insulators(TCIs)[32–36]offer an ideal material base for realizing magnetic Weyl semimetals.These materials are IV-VI semiconductors with a simple rocksalt structure.The nontrivial topology originates from the band inversion at four L points in the BZ,[33]which has been experimentally demonstrated by varying the Pb/Sn composition[35–38]or the temperature.[34]At the gap closing point,the low-energy band structure consists of a massless Dirac fermion at each L valley,which is equivalent to a pair of Weyl fermions with opposite chiralities.This Weyl pair can in principle be separated in momentum space by spin splitting in a Zeeman field,[39]resulting in the desired magnetic Weyl semimetal.In this regard,it was established decades ago that very diluted magnetic doping can induce ferromagnetic order in SnTe and other IV–VI semiconductors.[40,41]Numerous following experimental and theoretical studies have shown that the exchange coupling between magnetic moments and itinerant electrons is strong and the resulting spin splitting is relatively large.[42–53]These unique properties make IV–VI semiconductors,especially those near the topological phase transition,attractive in pursuing magnetic Weyl semimetals.

In this work,based on k·p theory and realistic tight binding(TB)calculations,we report the theoretical discovery of the Weyl semimetal phase in magnetized IV–VI semiconductors Sn1−xPbx(Te,Se).The pair of Weyl points near each L point are widely separated in momentum space by as large as 0.05˚A−1,and all Weyl points have nearly the same energy due to the high crystal symmetry.In addition,by tuning Pb/Sn composition or applying magnetic field,external pressure or strain,one can create,manipulate and annihilate Weyl points in momentum space,and achieve a sequence of topological phase transitions between Weyl semimetals and ferromagnetic insulators in both trivial and TCI phase.

PbxSn1−x(Te,Se)are narrow-gap semiconductors with band gap minima at L points.The low-energy properties near Lj(j=1,2,3,4)can be well described by the massive Dirac fermions and the k·p Hamiltonian is[54]

where{ aaaj, bbbj, eeej}is a local orthogonal coordinate system at Ljwith eeejalong ΓLjdirection and aaajperpendicular the plane containing Γ and Lj(see Fig.1),and kkk is the momentum relative to Lj.σz=±1 represent the p-orbital on the cation and anion respectively,and szlabels the total angular momentum jz=±1/2 along eeejdirection.Based on symmetry analysis of point group D3d,one can deduce the general form of exchange couple between conducting electrons and local magnetic moment SSS[47,48]

where gk,g0k,g⊥and g0⊥are the exchange coupling parameters,andare the components of magnetization along aaaj,bbbj,and eeej.WecansetA=so that A and a1(B and b1)represent the exchange coupling between conduction bands(valence bands)and the out-of-plane and in-plane components of the magnetic moments,respectively.Since there is continuous rotation symmetry C∞zin H0j( kkk)to the linear order in k,we can safely assume Sy=0 without loss of generality.One should be reminded that the k·p model to the linear order in k has more symmetries than the real system:the little group at L is enhanced from D3dto D∞h,generated by rotation along eee,Cn,a vertical mirror plane,Mx( aaa→− aaa)and a mirror plane that flips ke,Mz( eee→− eee).This entails,as we will later see,that some band crossings in this effective model are not protected when higher-order terms are included.

In the presence of ferromagnetic ordering,both the conduction and the valence bands become spin-split and the splitting increases with the exchange field(or the magnetization)as shown in Fig.2,and the top valence band and the bottom conduction band approaches each other,until the gap closes at a critical point If we further increase the exchange coupling,a band inversion between the top valence band(TVB)and bottom conduction band(BCB)occurs.It is well known that two non-degenerate bands cannot fully anti-cross each other in a 3D BZ after band inversion,but cross each other at an even number of discrete Weyl points in general.[55]

Fig.1.(a)Bulk Brillouin zone(BZ)with four equivalent L points and(b)schematic show of all the phases:normal insulator(NI),topological crystalline insulator(TCI),and Weyl semimetal,varying with the mass m and magnetization| SSS|.

Below, we discuss two special cases where the magnetization is along some high-symmetry directions.When SSS k[111],the rotation symmetry Czand the mirror reflection Mzare preserved.IfAB>0,we find TVB and BCB transform differently under Czrotation symmetry but identically under Mzmirror symmetry.Since two bands can only cross when they have different quantum numbers,we know that the crossing points in aaa bbb plane will be come anti-crossing and the gapopens,while the crossing along eee persists to form a pair of Weyl points(Fig.2(a)).Instead,for AB<0,the crossing bands have the same Czeigenvalue but different Mzeigenvalues,resulting in a nodal line crossing on the ab-plane(Fig.2(b)).It should be noted,however,that the mirror symmetry Mzis an artifact of the lineared k·p theory,instead of a crystal symmetry in a real rocksalt structure.Therefore,the nodal line on ab-plane will generically degrade into two Weyl points.Next we discuss the case where SSS k aaa.Similarly,there could either be two Weyl points along aaa (a1b1<0)or a nodal line in the bbb eee plane(a1b1>0)protected by Mxmirror symmetry.Different from the previous case is that Mxis an exact symmetry of the rocksalt structure,and hence the nodal line in this case is robust against all high-order terms.For a generic magnetization not along any high-symmetry line or plane,the band crossing points are two Weyl points.Firstly we ignore in-plane magnetic moment,and we should get a pair of Weyl points along eee or nodal lines in aaa bbb-plane;then,we take into account of the effect of in-plane magnetic moment.Based on the mirror symmetry,it will only shift the location of Weyl points along the in-plane magnetic moment direction or change the nodal line into a pair of Weyl points located in the plane spanned by eee and SSS.

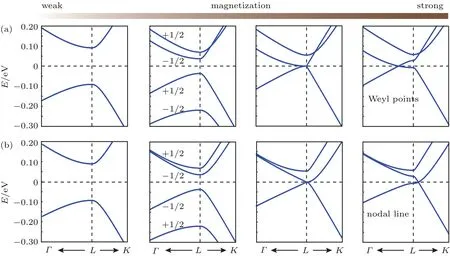
Fig.2.Bands evolution with the increase of out-of-plane magnetization along Γ L direction.There could be Weyl points along Γ L line with AB>0(a)or nodal lines in kz=0 plane with AB<0(b).±1/2 label different eigenvalues of total angular momentum jz=±1/2.

Now we turn to the analysis for all the four L points in the whole BZ.Since these materials have rock-salt structure with high cubic symmetry,the easy magnetic axes could be h111i,[51,52]h110i or h001i.As shown in Fig.1 and Fig.3,if the magnetization is along[001]direction,all the four L points are equivalent,related by the rotation and mirror symmetry,setting all the Weyl points at the same energy and located in the Γ L0L2or Γ L1L3plane based on the previous analysis;if the magnetization is along[111]direction,the four L points will be divided into two groups:L0and L1,2,3.Near L0,there is a pair of Weyl points along ΓL0direction,while near L1,2,3,there is a pair of Weyl points in the ΓL0L1,2,3plane;if the magnetization is along[1¯10],the four L points will also be divided into two groups,L0,2and L1,3.More interesting,if a1b1>0,we simultaneously obtain two nodal lines around L0,2points in ΓL0L2plane and two pairs of Weyl points around L1,3points.

Based on the k·p analysis above,we obtain a schematic phase diagram as shown in Fig.1(b).Without exchange field,the materials could be a normal insulator(m>0)or a topological crystalline insulator(m<0).At the phase transition point m=0,there will be Dirac points at L points,and any finite exchange field will generically separate the Dirac points into pairs of Weyl points with opposite Chern number and thus drive the materials into Weyl semimetal phase.For finite m,either inverted or not,when the exchange coupling is sufficiently strong to make mc>|m|,the Weyl semimetal phaseis realized.It was well known that the mass term can be well tuned experimentally by varying temperature,[34]changing the Pb/Sn composition,[35–38]or under internal distortion[56]or external strain,[57]while magnetization,both direction and magnitude,can be tuned by an external magnetic field.[51,52,58]All those properties make these materials have high tunability and thus potentially suitable to study the creation and annihilation of Weyl points.

One of the most interesting properties of Weyl points is that there will be the presence of Fermi arcs ending at the projections of two Weyl points with opposite Chern number.The Fermi arcs are the energy contour of the helicoid Riemann surface states.[59]We can deduce the Fermi arcs based on the locations of Weyl points in the bulk BZ from the bulk-boundary correspondence as shown in the Fig.3.If magnetization is along[001]direction,all the four L points can be related by rotation and mirror symmetry,and hence there is a strong confinement for the four pairs ofWeyl points. For example,L0and L2are related by reflection symmetry Z→−Z,and therefore the two Weyl points that are projected to the same momentum on(001)surface BZ must carry opposite Chern number as shown in the Fig. 3(a). In this case, there will be no open Fermi arcs on(001)surface,but only closed Fermi loops compose of two Fermi arcs.All these loops can,in principle,shrink to discrete points after adjusting the surface potential;for the(111)surface,all the four pairs of Weyl points are projected to different surface momenta,and there will be robust gap less surface states(Fermi arcs)against any local perturbations.If the magnetization is along[111]direction,for(001)surface,X¯1and X¯2are no longer equivalent,thus all the Weyl points are projected to different surface momenta,leading to four different Fermi arcs as shown in Fig.3(b).However,for(111)surface,the pair of Weyl points around L0are projected to the sameΓ¯point,and there will be no topological protected surface states,but other pairs of Weyl points around L1,2,3points will be projected to different surface momenta alongand connected by the nontrivial Fermi arcs.

To further study the material realization and detailed Fermi arcs in the surface BZ,we employed the realistic TB calculations[60]by adding additional exchange coupling in the p orbital fitted to previous experimental and theoretical studies.[42–48]Here,we take Sn1−xPbxTe as examples,which could be a Dirac semimetal at topological phase transition critical point x≈0.65.This TB model was widely used in the past,[60–62]well reproduced experimental bulk electronic structure,[63,64]and predicted nontrivial topological surface states[65]recently confirmed by experiment.[37]In all previous experimentally studied materials,[47]A and B always have the same sign,thus we will always got four pairs of Weyl points.In addition,the distance between a pair of Weyl points in momentum space can reach as large as 0.05˚A−1,within the ARPES resolution.To calculate the Fermi arcs,we employed the recursive Green function method[66]to simulate the semiinfinite slab,and the corresponding results are shown in Fig.3.It is clear that the calculated Fermi arcs are consistent with the k·p analysis.If magnetization is along[001]direction,it is indeed that only(111)surface exhibits Fermi arcs and for[111]magnetization,both(001)and(111)surface states have Fermi arcs.Moreover,the whole Fermi surface is from the non-trivial gapless surface states,which implies that the material is indeed a clean Weyl semimetal with Fermi energy at or very close to the energy of the Weyl points.

Fig.3.Schematic show of Weyl points in the whole BZ and Fermi arcs on(001)and(111)surface with magnetization SSS along[001]direction(a)and[111]direction(b).Red circle and blue dot represent the Weyl points carrying+and − Chern number.Panels(c)–(h)are the Fermi arcs directly calculated based on realistic TB model based the previous experimental parameters.Panels(c),(e),(g)and panels(d),(f),(h)are the results for magnetization SSS along[001]direction and[111]direction.

The topology analysis can only tell us that there will gapless Riemann surface states and unclosed Fermi arcs on certain surfaces,but the details of those states depend crucially on surface conditions in real materials.For example,there are dramatic differences between the Fermi arcs on the Teterminated and Sn-terminated(111)surface as shown in the Fig.3.This suggests the possibility of using surface perturbations to disconnect and reconnect the Fermi arcs.As shown in Fig.4,by adding a local potential on the surface,we can successfully break the original Fermi arcs connecting Wi+and Wi−(i=1,2,3,4),and rewire the Fermi arcs to connect other Weyl points.Specifically,when U=0.30V,the Fermiarcs between the pairs ofW2+,4and W2−,4are disconnected,and the new connections between W2±and W4∓are established.When we further increase U to 0.34 V,the connection between W3+and W3−is broken and new Fermi arcs are formed between W3+(W3−)and W4−(W2+).Similar rewiring of Fermi arcs can be achieved by tuning the magnetization.As far as we know,the disconnection and reconnection of Fermi arcs have never been experimentally observed or even theoretically studied before,and our results may guide further exploration.

In general,the magnetic doping would increase the trivial gap,thus to realize the Weyl points,it is easier to start from TCI phase with inverted band ordering.However,it should be emphasized that the emergence of Weyl points does not rely on whether the bands are inverted or not,but only depends on the gap size and the exchange coupling of magnetization(Fig.1(b)).Therefore our analysis and conclusion can be safely applied to other IV–VI semiconductors such as GeTe.Remarkably,it was experimentally found Mn/Crdoped GeTe are very good ferromagnetic materials[67,68]and the Curie temperature could be even higher than 180 K.[69–72]Our analysis strongly suggests that Mn-doped GeTe could be Weyl semimetals under pressure.

Fig.4.The evolution of Fermi arcs varying with the local surface potentialspoints and(i=1,2,3,4)are connected by the Fermiarcs.Under different potentials,the Fermi arcs can be disconnected and rewired between different Weyl points with opposite Chern number.

In conclusion,we proposed that magnetic Weyl semimetal can be realized in magnetically-doped(Mn,Eu,Cr)PbxSn1−x(Te,Se)class of TCIs or the similar IV–VI semiconductors such as GeTe.Depending on the direction of magnetic polarization,the(001)and(111)surfaces exhibited rather different Fermi arcs.And those Fermi arcs can be rewired under local surface potential or external magnetic field,to realize the disconnection and reconnection between different Weyl points, which has not been observed in any experiment. All the results are based on the well-studied experimental parameters,and the separation of Weyl points in momentum space is as large as 0.05˚A−1.We,therefore,believe that it is highly possible to realize and detect the magnetic Weyl points in those materials.

Acknowledgements

We thank Günther Bauer,Tomasz Story and Tomasz Dietl for helpful discussions.J.Liu was supported by the MRSEC Program of the National Natural Science Foundation under Award No.DMR-1419807 and the Start Up Funding from HKUST.C.Fang was supported by the National Thousand-Young-Talents Program of China.L.Fu was supported by the DOE Office of Basic Energy Sciences,Division of Materials Sciences and Engineering under Award No.de-sc0010526.

[1]Weyl H 1929 Zeitschrift für Physik 56 330

[2]Wan X,Turner A M,Vishwanath A and Savrasov S Y 2011 Phys.Rev.B 83 205101

[3]Nielsen H and Ninomiya M 1982 Phys.Lett.B 130 389

[4]Son D T and Spivak B Z 2013 Phys.Rev.B 88 104412

[5]Liu C X,Ye P and Qi X L 2013 Phys.Rev.B 87 235306

[6]Potter A C,Kimchi I and Vishwanath A 2014 Nat.Commun.5

[7]Witten E 2015 arXiv preprint arXiv:1510.07698

[8]Young S M,Zaheer S,Teo J C Y,Kane C L,Mele E J and Rappe A M 2012 Phys.Rev.Lett.108 140405

[9]Weng H,Fang C,Fang Z,Bernevig B A and Dai X 2015 Phys.Rev.X 5 011029

[10]HuangSM,XuSY,Belopolski I,Lee CC,ChangG,WangB,Alidoust N,Bian G,Neupane M,Bansil A,et al.2015 Nat.Commun.6

[11]Xu S Y,Belopolski I,Alidoust N,Neupane M,Zhang C,Sankar R,Huang S M,Lee C C,Chang G,Wang B,et al.2015 Science 349 613

[12]Xu S Y,Alidoust N,Belopolski I,Yuan Z,Bian G,Chang T R,Zheng H,Strocov V N,Sanchez D S,Chang G,et al.2015 Nat.Phys.11 748

[13]Lv B Q,Weng H M,Fu B B,Wang X P,Miao H,Ma J,Richard P,Huang X C,Zhao L X,Chen G F,et al.2015 Phys.Rev.X 5 031013

[14]Lv B Q,Xu N,Weng H M,Ma J Z,Richard P,Huang X C,Zhao L X,Chen G F,Matt C E,Bisti F,et al.2015 Nat.Phys.11 724

[15]Yang L X,Liu Z K,Sun Y,Peng H,Yang H F,Zhang T,Zhou B,Zhang Y,Guo Y F,Rahn M,et al.2015 Nat.Phys.11 728

[16]Lu L,Fu L,Joannopoulos J D and Soljacic M 2013 Nat.Photon.7

[17]Lu L,Joannopoulos J D and Soljaˇci´c M 2014 Nat.Photon.8 821

[18]Lu L,Wang Z,Ye D,Ran L,Fu L,Joannopoulos J D and Soljaˇci´c M 2015 Science 349 622

[19]Burkov A A,Hook M D and Balents L 2011 Phys.Rev.B 84 235126

[20]Burkov A A and Balents L 2011 Phys.Rev.Lett.107 127205

[21]Xu G,Weng H,Wang Z,Dai X and Fang Z 2011 Phys.Rev.Lett.107 186806

[22]Fang C,Gilbert M J,Dai X and Bernevig B A 2012 Phys.Rev.Lett.108 266802

[23]Witczak-Krempa W and Kim Y B 2012 Phys.Rev.B 85 045124

[24]Kim H J,Kim K S,Wang J F,Sasaki M,Satoh N,Ohnishi A,Kitaura M,Yang M and Li L 2013 Phys.Rev.Lett.111 246603

[25]Bulmash D,Liu C X and Qi X L 2014 Phys.Rev.B 89 081106

[26]Dubˇcek T,Kennedy C J,Lu L,Ketterle W,Soljaˇci´c M and Buljan H 2015 Phys.Rev.Lett.114 225301

[27]Borisenko S,Evtushinsky D,Gibson Q,Yaresko A,Kim T,Ali M N,Buechner B,Hoesch M and Cava R J 2015 arXiv preprint arXiv:1507.04847

[28]Chang G,Xu S Y,Zheng H,Singh B,Hsu C H,Belopolski I,Sanchez D S,Bian G,Alidoust N,Lin H,et al.2016 arXiv preprint arXiv:1603.01255

[29]Yang K Y,Lu Y M and Ran Y 2011 Phys.Rev.B 84 075129

[30]Liu E,Sun Y,Kumar N,Muechler L,Sun A,Jiao L,Yang S Y,Liu D,Liang A,Xu Q,et al.2018 Nat.Phys.14 1125

[31]Wang Q,Xu Y,Lou R,Liu Z,Li M,Huang Y,Shen D,Weng H,Wang S and Lei H 2018 Nat.Commun.9 3681

[32]Fu L 2011 Phys.Rev.Lett.106 106802

[33]Hsieh T H,Lin H,Liu J,Duan W,Bansil A and Fu L 2012 Nat.Commun.3 982

[34]Dziawa P,Kowalski B J,Dybko K,Buczko R,Szczerbakow A,Szot M,Lusakowska E,Balasubramanian T,Wojek B M,Bernsten M H,et al.2012 Nat.Mater.11 1023

[35]Tanaka Y,Ren Z,Sato T,Nakayama K,Souma S,Takahashi T,Segawa K and Ando Y 2012 Nat.Phys.8 800

[36]Xu S Y,Liu C,Alidoust N,Neupane M,Qian D,Belopolski I,Denlinger J D,Wang Y J,Lin H,Wray L A,et al.2012 Nat.Commun.3 1192

[37]Yan C,Liu J,Zang Y,Wang J,Wang Z,Wang P,Zhang Z D,Wang L,Ma X,Ji S,et al.2014 Phys.Rev.Lett.112 186801

[38]Zeljkovic I,Okada Y,Serbyn M,Sankar R,Walkup D,Zhou W,Liu J,Chang G,Wang Y J,Hasan M Z,et al.2015 Nat.Mater.14 318

[39]Cho G Y 2011 arXiv preprint arXiv:1110.1939

[40]Story T,Ga?la?zka,Frankel R B and Wolff P A 1986 Phys.Rev.Lett.56 777

[41]Bauer G 1986 in MRS Proceedings,Vol.89(Cambridge:Cambridge University Press)p.107

[42]G´orska M and Anderson J R 1988 Phys.Rev.B 38 9120

[43]Pascher H,Röthlein P,Bauer G and von Ortenberg M 1989 Phys.Rev.B 40 10469

[44]Rothlein P,Pascher H,Bauer G and Tacke M 1990 Semicond.Sci.Technol.5 S147

[45]Galazka R R,palek J,Lewicki A,Crooker B C,Karczewski G and Story T 1991 Phys.Rev.B 43 11093

[46]Hofmann W,Fichtel U,Pascher H,Frank N and Bauer G 1992 Phys.Rev.B 45 8742

[47]Bauer G,Pascher H and Zawadzki W 1992 Semicond.Sci.Technol.7 703

[48]Dietl T,´Sliwa C,Bauer G and Pascher H 1994 Phys.Rev.B 49 2230

[49]de Jonge W J M,Swagten H J M,Eltink S J E A and Stoffels N M J 1990 Semicond.Sci.Technol.5 S131

[50]Story T,Grodzicka E,Witkowska B,Gorecka J and Dobrowolski W 1992 Acta Physica Polonica A 82 879

[51]Eggenkamp P,Story T,Swüste C,Swagten H and de Jonge W 1993 Acta Physica Polonica A 84 641

[52]Eggenkamp P,Swagten H,Story T and de Jonge W 1995 J.Magn.Magn.Mater.140–144 2039

[53]Geist F,Herbst W,Mej´ıa-Garc´ıa C,Pascher H,Rupprecht R,Ueta Y,Springholz G,Bauer G and Tacke M 1997 Phys.Rev.B 56 13042

[54]Mitchell D L and Wallis R F 1966 Phys.Rev.151 581

[55]Murakami S 2007 New J.Phys.9 356

[56]Okada Y,Serbyn M,Lin H,Walkup D,Zhou W,Dhital C,Neupane M,Xu S,Wang Y J,Sankar R,et al.2013 Science 341 1496

[57]Qian X,Fu L and Li J 2014 Nano Res.8 967

[58]Brodowska B,Dobrowolski W,Arciszewska M,Slynko E and Dugaev V 2006 J.Alloys Compd.423 205

[59]Fang C,Lu L,Liu J and Fu L 2015 arXiv preprint arXiv:1512.01552

[60]Lent C S,Bowen M A,Dow J D,Allgaier R S,Sankey O F and Ho E S 1986 Superlattices and Microstructures 2 491

[61]Liu J,Hsieh T H,Wei P,Duan W,Moodera J and Fu L 2014 Nat.Mater.13 178

[62]Liu J,Qian X and Fu L 2015 Nano Lett.15 2657

[63]Wojek B M,Buczko R,Safaei S,Dziawa P,Kowalski B J,Berntsen M H,Balasubramanian T,Leandersson M,Szczerbakow A,Kacman P,et al.2013 Phys.Rev.B 87 115106

[64]Safaei S,Kacman P and Buczko R 2013 Phys.Rev.B 88 045305

[65]Liu J,Duan W and Fu L 2013 Phys.Rev.B 88 241303

[66]Sancho M P L,Sancho J M L and Rubio J 1985 J.Phys.F:Metal Phys.15 851

[67]Fukuma Y,Asada H,Nishimura N and Koyanagi T 2003 J.Appl.Phys.93 4034

[68]Dziawa P,Knoff W,Domukhovski V,Domagala J,Jakiela R,Lusakowska E,Osinniy V,Swiatek K,Taliashvili B and Story T 2007 Narrow Gap Semiconductors(Springer)pp.11–14

[69]Fukuma Y,Asada H,Moritake N,Irisa T and Koyanagi T 2007 Appl.Phys.Lett.91 092501

[70]Fukuma Y,Asada H,Miyawaki S,Koyanagi T,Senba S,Goto K and Sato H 2008 Appl.Phys.Lett.93 252502

[71]Dietl T 2010 Nat.Mater.9 965

[72]Hassan M,Springholz G,Lechner R,Groiss H,Kirchschlager R and Bauer G 2011 J.Crystal Growth 323 363