Quantum interferometry via a coherent state mixed with a squeezed number state∗
2019-04-13LiLiHou侯丽丽YongXingSui眭永兴ShuaiWang王帅andXueFenXu许雪芬
Li-Li Hou(侯丽丽),Yong-Xing Sui(眭永兴),Shuai Wang(王帅),†,and Xue-Fen Xu(许雪芬)
1School of Mathematics and Physics,Jiangsu University of Technology,Changzhou 213001,China
2Department of Fundamental Courses,Wuxi Institute of Technology,Wuxi 214121,China
1.Introduction
Nonclassical resources,such as squeezed states and Fock states,are mainly resources and can improve the sensitivity of the phase estimation of the optical interferometer.The Mach–Zehnder interferometer(MZI)is an important optical interferometer,and with solely classical light,its phase sensi√tivity is bounded by the shot-noise limit(SNL)∆ϕSNL=1/N¯(N¯ is the mean number of photons used to perform the estimation).This limit can be surpassed by using nonclassical states of light,such as squeezed state,[1–8]N00N states,[9,10]and Fock states.[11–15]With the help of the nonclassical states,the phase sensitivity can approach the Heisenberg limit(HL)∆ϕHL=1/.[16,17]
The ultimate phase sensitivity achievable in an MZI with a generic input state ρinis given by the quantum Crame´r–Rao bound(QCRB),[14,18]∆ϕmin=FQis the quantum Fisher information.For an MZI,the quantum Fisher information depends only on quantum input states.[18]It is known that,for a lossless MZI,the N00N state in principle achieves the ultimate HL.[9,10]Unfortunately,these states are extremely fragile.[19,20]Another possible way to approach the HL sensitivity is through the injection of the twin-Fock state,|nia⊗|nib,into the first beam splitter of an MZI.[12]Actually,for n=1 and n=2,the twin-Fock state does produce an N00N-like state on the other side of the beam splitter.Thus the twin-Fock inputs for n=1 and n=2 have the same quantum Fisher information as the N00N state.[21]But the twin-Fock state is hard to generate.Therefore,in the current technology,it is still useful to consider the interferometer with a high-intensity classical state in one input port and a low intensity nonclassical state in the other input,as Cave’s original scheme of mixing the coherent state with the squeezed vacuum state(SVS)at the input of an MZI.[1]In 2008,Pezz´e and Smerzi[2]revived Cave’s original scheme.They showed that,based on the quantum Fisher information,when the coherent state and the SVS have a roughly equal intensity(ӣ/2 photons on average in each state),the phase sensitivity reaches the HL independently of the actual value of phase.Later,Seshadreesan et al.[4]proved that such an HL can be achieved by the parity measurement[22]in the case of the phase shift ϕ→0.Recently,Birrittella et al.used the Fock state instead of the SVS to improve the phase sensitivity,and they found that the phase sensitivity can also approach the HL for increasing n.[13]In addition,comparing with the mixing coherent state with the SVS,Birrittella et al.further found that the mixing coherent states with the squeezed single photon state(|r,1i)yield higher sensitivity in phase-shift measurements for the same squeezing parameter.[13]On the other hand,for fixed total mean photon number and squeezing parameter,Olivares et al.[23]found there is a threshold of the coherent amplitude interfering with the squeezing single photon state above which the squeezed single photon state can outperform the performance of the SVS(showing the highest quantum Fisher information).
In this paper,following the work in Ref.[13],we consider the mixing of a coherent state and squeezed number state(SNS)with arbitrary photons n as the input state of an MZI,i.e.,

where|ziais a coherent state and|r,nibis an SNS.And then,based on the quantum Fisher information and parity measurement,[22,24]we investigate the prospect of performing phase estimation with such an input state in detail.Different from those studies in Refs. [13] and [23], for a fair comparison,within a constraint on both the total mean photon number ӣ of the input state|ini and the mean photon number of the SNS(or SVS),we re-examine whether the SNS can indeed improve the phase sensitivity for all values of phase shift?Our work is also enlightened by Lang and Caves’s work.[25]Via the analysis the quantum Fisher information,Lang and Caves have proved that the SVS is the optimal state to inject the other input port for achieving high-sensitivity phase-shift measurements within a constraint on the mean photon number,when one input of an interferometer is entered by coherent light.Theoretically,an SNS is obtained by performing the squeezing parameter(r)on an initial Fock state|ni,that is,

where

with the squeezing parameter r.[26]An SNS can be generated in experiment when the Fock state is entered into a squeezed generating device,such as a parametric amplifier.For squeezed single photon state(ˆS(r)|1i),it also can be generated starting from an SVS by means of the photon subtraction technique[27,28]or photon addition technique.[29,30]Mathematically,the scenario under our consideration covers two special cases of significance.(i)When n=0,|r,0ibis an SVS,then|ini reduces to the input state in Ref.[1].(ii)When r=0,|0,nibis a number state,and then this produces a special case of the state investigated in Refs.[13]and[14].
The paper is arranged as follows.In Section 2,for an MZI with the SNS-coherent input state,we obtain the quantum Fisher information.We find that,for a given fixed total mean photon number and the mean photon number of the SNS(or SVS),SVS-coherent state indeed gives a larger quantum Fisher information than SNS-coherent state.In Section 3,we analytically prove that the classical Fisher information for parity measurement saturates the quantum Fisher information when the phase shift approaches zero.Thus,the phase sensitivity can saturate the QCRB at ϕ=0 via parity measurement.For a given fixed total mean photon number and the mean photon number of the SNS(or SVS),we show that SNS-coherent state can offer better phase sensitivity via the parity detection only when the phase shift deviates from the optimal phase ϕ=0.
2.Quantum Fisher information in an MZI
The balanced MZI considered here is mainly composed of two 50:50 beam splitters and two phase shifters.As was shown by Yurke et al.,[31]the first beam splitter BS1 is described by the transformation

And the operator representation of the second beam splitter BS2 is taken as

The operatorUˆ(ϕ)=exp?iϕ?2?denotes the two phase shifters,the angle ϕ is the phase shift between the two arms to be estimated.According to the work in Ref.[31],the unitary transformation associated with such balanced MZI can be written as
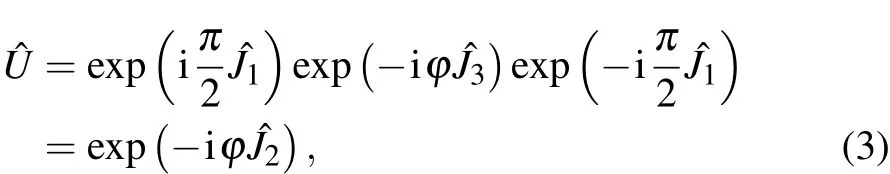
where these operators consisted of two sets of Boson operators

are the angular momentum operators in the well-known Schwinger representation.They satisfy the commutation relationand commute with the Casimir operatorFor an input state propagating through the MZI,the resulted output state can be written as

Applying the following transformation relations

and the relationin principle,one can obtain the explicit form of the output state the MZI.
Here,we first give the quantum Fisher information for the interferometer state|ini=|zia⊗|r,nib.The ultimate limit of phase sensitivity is given by the QCRB[18]

For pure states injected into an MZI,the quantum Fisher information FQcan be obtained by[32]

where

is the state just before the second beam splitter of the MZI,and|ψ0(ϕ)i= ∂ |ψ(ϕ)i/∂ϕ.In terms of the input state,the quantum Fisher information becomes
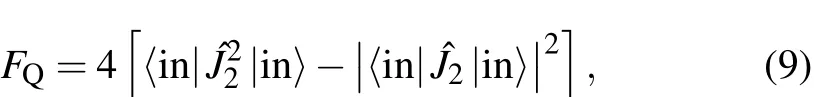
and thus the quantum Fisher information is,up to factor of 4,the variance of the operatorWhen the SNS-coherent state is considered as the input state,the quantum Fisher information can be directly obtained as

where=|z|2(z=|z|eiθthe amplitude of the coherent state and we have set θ=0 in order to obtain the maximized Fisher information).In Eq.(10),¯nSNSis the average photon number of the SNS,i.e.,

For an ideal MZI,the total mean photon number(ӣ=)is a conserved quantity.For a constraint on the total mean photon number,it is easily proved that the quantum Fisher information given by Eq.(10)is maximized by splitting the photons equally between the two modes,i.e.,Obviously,when n=0,one can obtain the quantum Fisher information for the input state with SVS-coherent state(|zia⊗|r,0ib),[2]
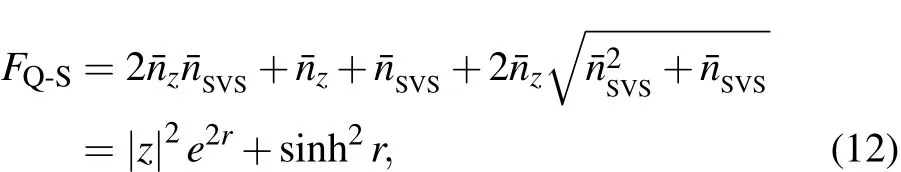
where=sinh2r the mean photon number of the SVS.On the other hand,in the case of r=0,the input state reduces to a coherent state mixed with a Fock state(|zia⊗|0,nib)and one can directly obtain the quantum Fisher information for this input state[14]

In addition,based on Eq.(10),one can see that,for a given fixed total mean photon numberN¯ and the mean photon number of the SNS(or SVS),the SVS-coherent input state gives a larger quantum Fisher information than SNS-coherent one.In order to obtain large quantum Fisher information,one would like to enhance the squeezing factor r as much as possible.However,this experimentally challenging.[33–35]The maximum reported squeezing parameter was about r≈2.3(i.e.,15 dB).[34]Therefore,in order to enhance the mean photon number of squeezed states for a given r,SNS may be an alternative resource in quantum metrology.Especially,squeezed single photon state S(r)|1i can be generated by applying photon subtraction on an SVS in experiment.[27,28]
3.Parity measurement and phase sensitivity
Up to the present,people have known that the quantum CRB ∆ϕmincan be reached at particular values of the phase shift by detecting the photon number parity on one of the output modes.For the detailed discussion of the parity detection in quantum optimal metrology,one can review that in Refs.[22]and[24].Actually,the parity measurement is to obtain the expectation value of the parity operator in the output state of the MZI.For mode b,the parity operator can be written as

where|γi is a coherent state.Then the expectation value of the parity operator can be obtain by
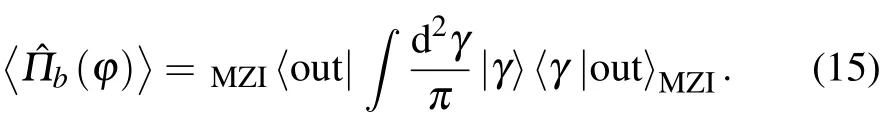
Thus,if one knows the output state of the MZI, one can present the parity-based phase estimation scheme with calculation of the average signal?ˆΠb?and phase sensitivity.
When the product state|zia⊗|r,nibis injected into the MZI,we obtain the expectation value of the parity operator in the output state[See Appendix A]

where
is the corresponding expectation value of the parity operator for the input state with SVS-coherent state,[4]

In the following,we shall mainly investigate the corresponding phase sensitivity with parity measurement.
Now we turn to the discussion of the phase sensitivity.The classical Fisher information FCis given by[36,37]

where i denotes the outcome of the measurement and P(i|ϕ)is the probability of the measurement resulting in the i-th outcome conditioned on a specific value of the phase shift ϕ.For parity measurement,there are only two outcomes,+for even and−for odd,and the corresponding probabilities of even and odd counts

Then notingˆΠ2=1,and substituting Eq.(19)into Eq.(18),one can obtain the classical Fisher information for parity measurement[24]

Therefore,according to the CRB theory,the phase sensitivity of parity measurement can be directly determined from the average signal?ˆΠ?

Compared Eq.(20)with Eq.(10),for the small values of n and by the Taylor expansion of Eq.(16)around ϕ=0,we can analytically prove that the classical Fisher information indeed equals the quantum Fisher information in the case of ϕ=0.For the general values of n,we can numerically prove this conclusion is still ture.Therefore,the phase sensitivity can saturate the QCRB at ϕ=0 via parity measurement.
By Eqs.(16)and(21),for some values of n and given the amplitude of the coherent state z=10,we firstly investigate the hΠbi as a function of the phase shift ϕ.From Fig.1(a),one can see that,for a given initial squeezing parameter r,the central peaks of the hΠbi of the SNS-coherent input states are narrower than that of the SVS-coherent input state.This is because,for a given parameter r,the SNS carries more photons.For a fair comparison between SNS and SVS,settingwe repeat these graphs in Fig.1(b).Figure 1(b)shows that,in the case of,the distributions of these central peaks of the hΠb(ϕ)i near ϕ =0 are almost identical.But,for somewhat large values of the phase shift, figure 1 also shows that the average signal hΠbi of the SNS-coherent state blows up and is more sensitivity to the phase shift than that of the SVS-coherent one,which may be benefit to improving the phase sensitivity for somewhat large values of ϕ as shown in the following.

Fig.1.The expectation value of the parity operator versus the phase shift ϕ for both SNS-coherent and SVS-coherent as input states of the MZI,respectively.(a)Given the initial squeezing parameter r=0.6 and z=10;(b)givenn¯SNS=n¯SVSand z=10.For a more obvious comparison,we have adjusted the negative central peak value to a positive value.

Fig.2.Plots of the phase uncertainty versus total average photon at ϕ=10−4for both the SNS-coherent state and the SVS-coherent state,along with the corresponding curves for the SNL and the HL limits.Only the parameter z is being changed.(a)Given the initial squeezing parameter r=0.6;(b)Given
Secondly,we investigate how the phase sensitivities change with the total mean photon number based on Eqs.(16)and(21).Obviously,for given an initial squeezing parameter r,the phase sensitivity increases with the number n as shown in Fig.2(a).This is also because,for a given parameter r,the SNS with large number n can carry more photons.However,for given the same ratios of¯nSNS/ӣ and¯nSVS/ӣ,we can obtain almost the same phase sensitivity for all values of n as shown in Fig.2(b).Although,within a constrain on the total mean photon number,the SVS is the optimal state when one input of an interferometer is entered by coherent light,[25]one can see from Fig.2(b)that the difference among those phase sensitivities coming from both the SNS-coherent and the SVS-coherent is very small,especially when they carry many photons.Thus,SNS may be considered an alternative resources in the quantum metrology.
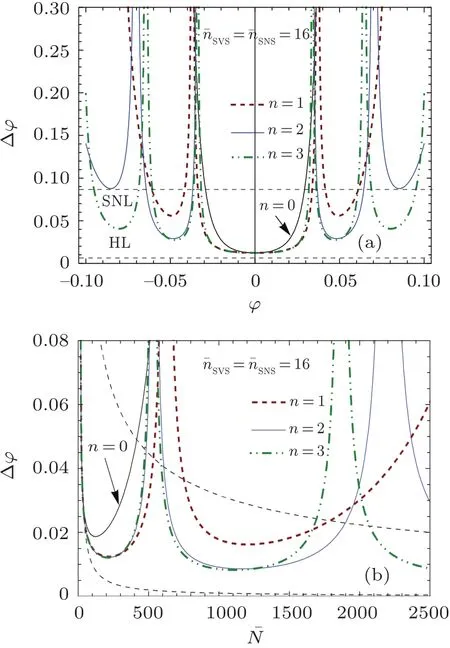
Fig.3.(a)For give=16 and z=10,the phase sensitivity∆ϕ as a function of the phase shift ϕ when the SNS-coherent state,and the SVS-coherent state as interferometer states;(b)For given=16 and ϕ=0.15,the phase sensitivity∆ϕ as a function of the total mean photon number.Only the parameter z is changed.
From the above discussion,we can see that our results obtained via both the quantum Fisher information and the parity measurement support Lang and Caves’s work.[25]However,as pointed in Ref.[4],the parity measurement scheme(or the Ono–Hofmann detection scheme)is highly affected by the deviation of the optimal phase shift ϕ.Here,we also investigate how the phase sensitivity varies with ϕ via the parity measurement.Based on Eqs.(16)and(21),we plot the phase sensitivity as a function of the phase shift ϕ in Fig.3(a).Obviously,when the phase shift somewhat deviates the optimal phase ϕ=0,the SNS can give better sensitivity than the SVS via parity measurement.In addition,SNS-coherent input state provides sub-SNL for a much broader range of the accumulated phase shift ϕ,especially for large number n.In Fig.3(b),for somewhat large value of the phase shift,we show that how the phase sensitivities change with the total mean photon number.In the latter case especially,we see that the SNS-coherent state indeed give better sensitivity when the phase shift deviates ϕ=0.When the total mean photon number increases,the phase uncertainties blow up due to the periodic nature of the average signal of hΠbi,but there are other photon numbers where the phase sensitivity is still below the SNL for for SNS,especially when the number n increases.
Since parity measurement achieves maximal phase sensitivity at particular values of phase ϕ,its applicability,in general is restricted to estimating “local”phase.[24]Local parameter estimation is concerned with detecting small changes in parameter that are more or less known,as opposed to the“global”one,wherein a complete lack of knowledge about parameter is initially assumed.[38]Therefore,performing phase estimation starts with SNS-coherent input state is a alternative choice,which can offer roughly knowledge about the value of the accumulated phase.And then,one can move the accumulated phase closer to the optimal phase ϕ=0 and improve phase sensitivity.
4.Conclusions
In summary,we have studied the quantum optical interference by mixing a coherent state with a SNS.Given a total mean photon number and the mean photon number of the SNS(or SVS),our results show that the quantum Fisher information of the SNS-coherent is almost equals to that of the SVS-coherent one,although SVS-coherent provides somewhat large quantum Fisher information.We prove that the classical Fisher information for parity measurement saturates the quantum Fisher information when the phase shift approaches zero.Thus,the quantum Cram´er–Rao bound can be reached via the parity measurement in the limit ϕ → 0.We also show that,for fixed a total mean photon number and the mean photon number of the SNS(or SVS),SNS-coherent can offer better phase sensitivity via the parity detection only when the phase shift deviates from the optimal phase ϕ=0.
Appendix A:Deriving of Eq.(16)
For convenience,we adopt the following form of the

SNS[39]where Hn(x)is a Hermite polynomials.It can be seen from Eq.(A1)that the SNS can be actually considered as a Hermite polynomial excited SVS.In the basis of the coherent state,the SNS can be further expressed by
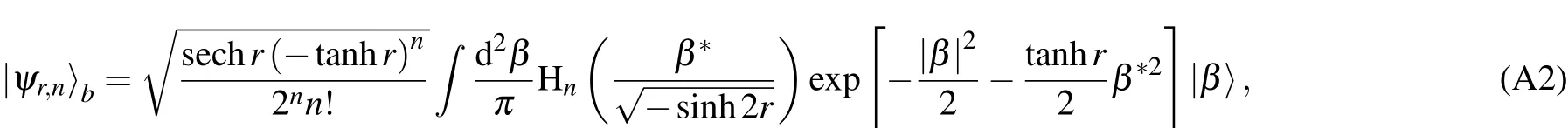
where|βi=exp?−|β|2/2+βb†?|0i is a coherent state.When the product state|ini=|zia⊗|ψr,nibis injected into the MZI,by Eqs.(5)and(6),the resulted output state can be written as

which is the state of light at the output of the MZI.Then substituting Eq.(A3)into Eq.(15),and applying the integral formula[40]
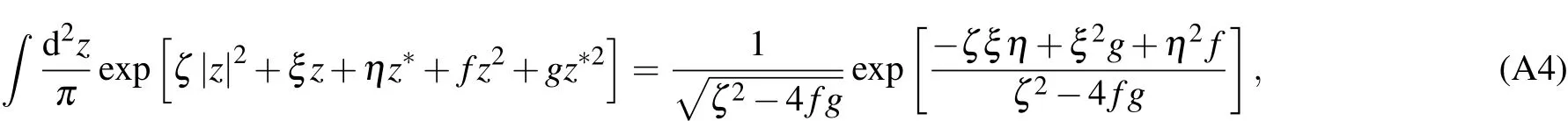
whose convergent condition is Re(ξ± f±g)<0 andAfter a long calculation,we obtain the expectation value of the parity in the output state of the MZI as shown in Eq.(16).
On the other hand,noting that the generating function of Hermite polynomial Hm(x)[41]

and the well-known differential relations of Hm(x)
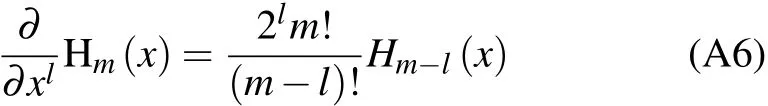
we can also rewrite Eq.(16)in a compact form,i.e.,

where

[1]Caves C M 1981 Phys.Rev.D 23 1693
[2]Pezz´e L and Smerzi A 2008 Phys.Rev.Lett.100 073601
[3]Anisimov P M,Raterman G M,Chiruvelli A,Plick W N,Huver S D,Lee H,and Dowling J P 2010 Phys.Rev.Lett.104 103602
[4]Seshadreesan K P,Anisimov P M,Lee L,and Dowling J P 2011 New J.Phys.13 083026
[5]Oh C,Lee S Y,Nha H,and Jeong H 2017 Phys.Rev.A 96 062304
[6]Yu X D,Li W,Zhu S Y,and Zhang J 2016 Chin.Phys.B 25 020304
[7]Li H M,Xu X X,Yuan H C and Wang Z 2016 Chin.Phys.B 25 104203
[8]Xu L and Tan Q S 2018 Chin.Phys.B 27 014203
[9]Lee H,Kok P and Dowling J P 2002 J.Mod.Opt.49 2325
[10]Dowling J P 1998 J.Mod.Opt.45 2233
[11]Kuzmich A,Manning D,Mandel L,and Walmsley I A 1998 J.Mod.Opt.45 2233
[12]Campos R A,Gerry C C and Benmoussa A 2003 Phys.Rev.A 68 023810
[13]Birrittella R,Mimih J,and Gerry C C 2012 Phys.Rev.A 86 063828
[14]Pezz´e L and Smerzi A 2013 Phys.Rev.Lett.110 163604
[15]Wang S,Wang Y T,Zhai L J and Zhang L J 2018 J.Opt.Soc.Am.B 35 1046
[16]Ou Z Y 1996 Phys.Rev.Lett.77 2352
[17]Holland M J and Burnett K 1993 Phys.Rev.Lett.71 1355
[18]Braunstein S L and Caves C M 1994 Phys.Rev.Lett.72 3439 Braunstein S L and Caves C M 2007 Phys.Rev.Lett 40 2799
[19]Rubin M A and Kaushik S 2007 Phys.Rev.A 75 053805
[20]Jiang K,Brignac C J,Weng Y,Kim M B,Lee H and Dowling J P 2012 Phys.Rev.A 86 013826
[21]Lang M D and Caves C M 2014 Phys.Rev.A 90 025802
[22]Gerry C C and Mimih J 2010 Contemp.Phys.51 497
[23]Olivares S,Popovic M and Paris M G A 2016 Quantum Mean.Quantum Metrol.3 38
[24]Seshadreesan K P,Kim S,Dowling J P and Lee H 2013 Phys.Rev.A 87 043833
[25]Lang M D and Caves C M 2013 Phys.Rev.Lett.111 173601
[26]Kim M S,de Oliviera F A M and Knight P L 1989 Phys.Rev.A 40 2494
[27]Wenger J,Tualle-Bouri R and Grangier P 2004 Phys.Rev.Lett.92 153601
[28]Olivares S and Paris M G A 2005 J.Opt.B:Quantum Semiclass.Opt.7 S616
[29]Dell’Anno F,De Siena S and Illuminati F 2006 Phys.Rep.428 53
[30]Kim M S 2008 J.Phys.B:At.Mol.Opt.Phys.41 133001
[31]Yurke B,McCall S L and Klauder J R 1986 Phys.Rev.A 33 4033
[32]Ben-Aryeh Y 2012 J.Opt.Soc.Am.B 29 2754
[33]Vahlbruch H,Mehmet M,Chelkowski S,Hage B,Franzen A,Lastzka N,Goßer S,Danzmann K and Schnabel R 2008 Phys.Rev.Lett.100 033602
[34]Vahlbruch H,Mehmet M,Danzmann K and Schnabel R 2016 Phys.Rev.Lett.117 110801
[35]Schnabel R 2017 Phys.Rep.684 1
[36]Hall M J W 2000 Phys.Rev.A 62 012107
[37]Uys H and Meystre P 2007 Phys.Rev.A 76 013804
[38]Durkin G A and Dowling J P 2007 Phys.Rev.Lett.99 070801
[39]Meng X G,Wang Z,Fan H Y and Wang J S 2012 J.Opt.Soc.Am.B 29 1835
[40]Puri R R 2001 Mathematical Methods of Quantum Optics(Berlin:Springer-Verlag,2001),Appendix A
[41]Rainville E D 1960 Special Function(New York:MacMillan)
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Effect of carrier mobility on performance of perovskite solar cells∗
- Plasma electrolytic liquefaction of sawdust∗
- Insight into band alignment of Zn(O,S)/CZTSe solar cell by simulation∗
- Effect of terahertz pulse on gene expression in human eye cells∗
- Ultraviolet photodetectors based on wide bandgap oxide semiconductor films∗
- A primary model of decoherence in neuronal microtubules based on the interaction Hamiltonian between microtubules and plasmon in the neurons
