Entangled multi-knot lattice model of anyon current∗
2019-04-13TieyanSi司铁岩
Tieyan Si(司铁岩)
Physics Department,School of Sciences,Key Laboratory of Microsystems and Microstructures Manufacturing-Ministry of Education,Harbin Institute of Technology,Harbin 150080,China
1.Introduction
Anyons in quantum many-body systems are exotic quasiparticles that bear special statistical character beyond that of fermions and bosons.It is the elementary unit for constructing fault-tolerant quantum computation.[1,2]An anyon can exist as a Majorana fermion or vortex core in a topological superconductor,and has been classified into the widespread existence of topological matter in recent years.[3]However,solid experimental manipulation of non-Abelian anyons remains a challenge so far.One promising candidate for experimental implementation of anyons is electron gas in a strong magnetic field.[4]Exchanging two Abelian anyons generates an arbitrary phase upon the wave function,[5]φ(r1,r2)=eiθφ(r2,r1),where θ ∈ [0,2π].The statistical phase can be controlled by the enclosed magnetic flux within the exchanging path loop.The interference fringes between Laughlin quasi-particles provide a controversial experimental signal of non-Abelian statistics[6]that is predicted by fractional quantum Hall theory.[4,7]Meanwhile,the experimental operation of Ising anyons suggested by conformal field theory of the critical two-dimensional(2D)Ising model[8]is still a difficult challenge for experiments.[9]
The plaquette vortex excitation in Kitaev’s toric code model[1]and honeycomb model[10]is a typical anyon in quantum lattice models,as is Wen’s toric code model and topological color code model on a 2D lattice.[11]Anyons also exist as fractional quasi-excitation states in the 1D optical superlattice.[12–14]In the toric code model,the plaquette excitation and vertex excitation form a dual pair of Abelian anyons.The exchanging of the two anyons is performed on a loop of lattice squares.Non-Abelian anyons exist in the gapless phase of the Kitaev honeycomb model.[10]In reality,it is difficult to find a solid material correspondence to the toric code model and honeycomb model,even though the physics of the Kitaev honeycomb model show relevance to certain transition metal compounds,such as(Na,Li)2IrO3iridates and RuCl3.[15]
Here we propose another different approach to anyons:periodically entangled knot current of hopping particles on lattice.The over-crossing points of many entangled knots are placed on a periodical lattice.The over-crossing states are mapped into the spin state.In this model,anyons exist as running particles in these entangled wires.For the anyon knot model on a square lattice,anyons are conventional positrons(or electrons)and magnetic monopoles.For the anyon knot model on the honeycomb lattice,we refer to three colors of anyons:red,blue,and yellow.These anyon knot models have exact correspondence with the 2D Ising model and Kitaev hon-eycomb model,as well as the Heisenberg model.Each eigenstate of the anyon knot model corresponds to a knot configuration.Each knot configuration bears a topological invariant Jones polynomial,which is related to the non-Abelian Chern–Simons field theory.[16]

Abelian Chern–Simons field theory suggests that many entangled knots are classified by the linking number,self-linking number,and writhing number.[17]The fusion rules of anyons have an explicit demonstration in this anyon knot model with the assistance of braiding operations.Unlike the braiding operation along the time lines,the braiding operation on a knot lattice is implemented on a spatial lattice.
The paper is organized into two sections.In the first section,we explore the anyon states and fusion rules on the square knot lattice model with long-range coupling interaction,which incorporate the two-state and three-state block spin to demonstrate the integral and fractional filling quantum Hall state,long-range hopping model,spin Hall model,and convective fermion current pairing model.In the second section,we construct a knot lattice on a honeycomb lattice to study non-Abelian anyons in quantum states in various long-range coupling quantum models.In the approximation of nearest neighbor coupling,this knot lattice model reveals the topological order in the conventional transverse Ising model,Kitaev honeycomb model,Haldane model,and topological flat band model.The topological change from one ordered state to another is distinguished by the variation of topological linking number.
2.Entangled anyon current knot on square lattice
2.1.Dual anyon pairs in long-range coupling knot lattice model of two-state spins
A knot is a closed loop in a 3D manifold that can map into a unit circle.Many entangled knots together define a link.We take M knot current that projects a horizontal current and N knot current that projects a vertical current,and entangle them to project a 2D M×N lattice of over-crossing(or under-crossing)points.If both the horizontal knots and vertical knots bend upward(downward),the base manifold of the over-crossing lattice is a sphere in the thermal dynamic limit(M,N→∞)(Figs.1(a)and 1(c)).If the horizontal knots bend upward and the vertical knots bend downward,the knot lattice is equivalent to a torus(Figs.1(b)and 1(d)).
The horizontal knot(black lines in Figs.1(a)and 1(b))could be implemented by electrical conductor wires,such as super-conducting wires.Only electrons or positrons run in the horizontal knot,while the vertical knot(purple lines in Figs.1(a)and 1(b))are currents for running magnetic monopoles with positive or negative magnetic charges.According to the electromagnetic induction effect,a running positron induces a circular magnetic field around the electric current.There exists an electromagnetic interaction between positrons and magnetic monopoles at each over-crossing point.If the magnetic current lies in the same direction as the induced magnetic field by the electric current according to the right-hand rule,then the energy of the system would increase by one unit.This is the case for Fig.1(e)(S=+1),where the upward magnetic current is above the left-moving electric current.On the contrary[Fig.1(e)(S=−1)],both the magnetic current and electric current are slowed down,and the energy of the system drops one unit.Each over-crossing point can be mapped into an effective Ising spin with two states,|↑i and|↓i.Under the action of the effective Hamiltonian Hz=Sz,the eigenvalues with respect to these two spin states are S=±1(Fig.1(e)).

Fig.1.(a)The lattice of over-crossing points with spherical periodic boundary condition.(b)The lattice of over-crossing points with torus periodic boundary condition.(c)Multilayer sphere of many layers of entangled knots.Each layer corresponds to a square lattice above.(d)Multilayer torus of many layers of entangled knots.(e)The mapping from over-crossing states of electric current and magnetic current to the two states of Ising spin.
The electromagnetic induction effect also introduces the long-range coupling interaction between different crossing sites,because if any one of the local crossing sites along the loop is cut,it would induce a global magnetic field that acts on the rest of the crossing sites.The magnetic monopole current generates a global electric field in the direction parallel to the electric current.The same phenomena occur for the electric current.Whenever an electric loop is cut into segments,the total magnetic flux loses one flux.All of the positrons along this electric current become static and lose their interaction with the magnetic monopole at the crossing point.Thus there exists a topological correlation between Ising spins in each loop.Therefore,we introduce a long-range coupling between spins along the same loop,
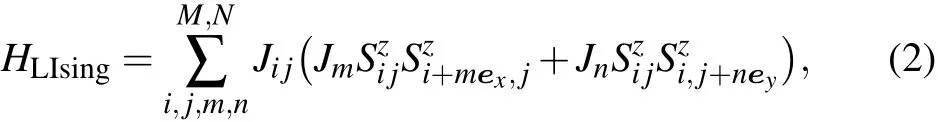
where Sz=±1.The correlation length is proportional to the length of the loop.This long-range coupling Ising model assigns different flipping probabilities on the crossing state from that assigned by the nearest-neighbor coupling Ising model.Non-Abelian anyons exist in this long-range coupling Isinglike knot model.
Every knot lattice configuration can be classified by a topological number called the linking number,which is defined as the total number of positive crossings minus the total number of negative crossings,Llink=(N+−N−)/2.This linking number is equivalent to the total magnetization of spins in the magnetic system,
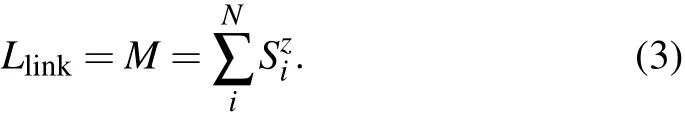
Thus,total magnetization is a topological invariant for one knot lattice configuration in this lattice model.Since every current segment is confined on a local lattice site,here the Reidemeister move in knot theory is strictly confined within one lattice site.Total magnetization is not a knot variant,because different knot configurations may share the same linking number.In physics language,different degenerated spin configurations may have the same magnetization value.Suppose the over-crossing state has the probability to flip from+1 to−1(or vice versa)under random cutting and reunite.A temperature T can be defined as a number that is positively correlated to this flipping probability.Then different knot lattice configurations have different existence probabilities with respect to the total energy and temperature.We assume that the knot lattice with lower total energy has a higher probability to exist at a fixed temperature,i.e.obeying the Maxwell distribution.Then this probability weight of a certain knot lattice configuration A follows the same rule as spins in statistical mechanics,

where Z is the partition function which summarizes the total probability of all possible configurations.As we know,each spin state flipping indicates a topological change of knot lattice,where the entanglement between two knots either increases or decreases by 1.Since the partition function is the summation of all possible knot lattice configurations,it is a topological invariant under arbitrary flipping operations.When the knot lattice configuration is exposed to an external electric field(or magnetic field)that is perpendicular to the knot lattice plane, the electric current of positrons (or magnetic current of monopoles)tends to stay above(or below).The probability of a certain knot configuration is determined by its linking number,which is equivalent to the effective Hamiltonian

here hirepresents the strength of the external field.Obviously the ground state knot configuration corresponds to the highest linking number,L=M×N.With the torus boundary condition,all the magnetic currents are above the electric currents at every over-crossing site.The magnetic monopole generates an electric field to propel the positrons in electric currents that pass through the inner zone enclosed by the magnetic loops.These magnetic loops cannot separate from electric loops without cutting.For the spherical boundary condition,it is equivalent to making a copy of the lattice and connecting it with the original lattice on the boundary point by point,but the magnetic current is below the electric current in the copied lattice.This case is equivalent to that of the torus boundary condition but with a larger linking number L=2M×N.The eigenvalue corresponds to the Hamiltonian Hzis Ei=−hLi,where Lirepresents the linking number with respect to the ith excited states.There are(MN−1)-fold degenerated first excited states with respect to L1=(MN−2).The average linking number reads,

where Z(h)is the partition function for the free spin Hamiltonian Eq.(5)with homogeneous external field h.
For a classical knot lattice of elastic wires,we introduce the coupling interaction between two nearest-neighbor crossing points.Two neighboring sites with opposite crossing states generate a kink between them that increases the elastic energy by one unit,while neighbors with the same over-crossing states bear a smooth crossover between them that decreases the elastic energy by one step.Thus the total energy of the knot lattice is
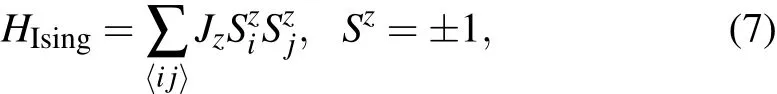
where Jz<0.Usually the coupling strength Jzbetween two spins,Jz=Jz(i,j),decreases if the distance between two spins(Sziand Szj)increases.The conventional Hamiltonian is not a topological invariant which is invariant under continuous transformation of the knot lattice.However,for this knot lattice model,the coupling strength between two spins within the same loop is induced by an electromagnetic wave which fills in the conducting channel at the speed of light.The coupling strength Jz(i,j)is independent of the separation distance between the two spins.In this case,the knot Hamiltonian is still a topological invariant,as is the partition function as well as other thermodynamic observables.In the ground state of this ferromagnetic ally coupled system,all over-crossings are oriented in the same direction.The transition from disordered orientation to this uniform ordering occurs at critical temperature Tc.[18]Since the topological linking number changes during this transition,we can also call this transition a topological phase transition.
The ground state of the ferromagnetic Ising model has two-fold degeneracy,i.e.,all spins either point up or down,|gi=|↑↑↑···↑↑↑i+|↓↓↓···↓↓↓i.For this knot lattice model,the ground state can be represented by two layers of multiknot sphere or multi-knot lattice(Figs.1(c)and 1(d)).The first excited state is generated by flipping one spin,thus|ei1=|↓↑↑ ···↑i+|↑↓↑ ···↑i+···+|↑↓↓ ···↓i+|↓↑↓ ···↓i+···.There must be 2MN layers of knot lattice in total to represent the first excited state(Figs.1(c)and 1(d)).Different knot configurations of the eigenstate can transform into each other by braiding anyons,i.e.,the positron and magnetic monopole.
The positron and magnetic monopole in this knot lattice model are dual anyons to each other.Each spin state is a collective wave function of two open fermionic strings of electric current or magnetic current.Since the two open strings are controlled by the four ending points at the middle point of each edge,the spin states here are also a collective wave function of four anyons on the interface(Figs.2(a)and 2(b)).The|↑i state can transform into|↓i by braiding the positron(e+)No.3and magnetic monopole(m+)No.4twice in a clockwise direction(Fig.2(a)),

Fig.2.(a)Flipping|↑i to|↓i by braiding the positron(e+)and magnetic monopole(m+)twice in a clockwise manner.(b)Flipping|↓i to|↑i by braiding e+and m+in a counterclockwise manner.

Since the spin state after braiding gains a phase factor eiπ,the statistical phase factor for e+and m+is=.Thus,the positron and magnetic monopole are dual anyons.Following the same process,braiding e+and m+in a counterclockwise direction leads to the same statistical phase(Fig.2(b)),i.e.,=eiπ/2.This braiding operation generates an intermediate vacuum state.The two strings(the green arc in Figs.2(a)and 2(b))in this state are forbidden from touching each other,which is why they are fermionic strings ψs.Since the monopole only runs in the vertical current,while the positron only runs in the horizontal current,the two fermionic strings are an effective converter that transforms a monopole into a positron,or vice versa.The vacuum state physically implemented the fusion rules of anyons(see the following Figs.2(a)and 2(b)),

and the trivial fusion rules:e×e=I,m×m=I,ψs×ψs=I.However,this braiding operation is only focused on one spin in one layer;it is not the eigenstate of the Ising model.
Braiding anyons in the eigenstate of the Ising model leads to more complicated statistical behavior beyond an Abelian phase factor.We consider a synchronous braiding of two anyons in the bilayer knot configuration of the Ising ground state(Figs.1(c)and 1(d)).The two layers of knot lattice keep conformal invariance,thus one can draw two lines out of their common center to locate the two anyons at the same projected position on the base manifold.Suppose the upper layer represents spin up|↑↑↑ ···↑↑↑i,while the bottom layer represents spin down|↓↓↓ ···↓↓↓i.If we flip one spin at the same site of the two layers,it would generate a quasi-particle in the first excited state.This spin flipping can be implemented by the braiding operation.At a given lattice site,we braid anyons of(|↑i+|↓i)in the two layers synchronously(Fig.3(a)).Upon one braiding in the clockwise direction,the upper layer spin transforms into a vacuum state,while the fermionic string in the bottom layer becomes non-trivially entangled with one crossing.The sum of these two knot configurations are not the eigenstate of the system.Furthermore,one more braiding brings the spin-up state in the upper layer to a spin-down state,while the spin in the bottom layer now becomes entangled electric current and magnetic current with two crossings on one site.The sum of the two layer states is still not the eigenstate of the system.That means these states are not physically accessible.In order to find the right knot configuration for the eigenstate,we have to introduce a Majorana fermionic operation(ψ)on the internal crossings within one site(Fig.3(a)).The output of this Majorana fermion is to flip the crossing state,performing the same action as Sxwhich is formulated into the Jordan–Wigner transformation,

Here,the raising operator and lowering operator have the familiar form,S+=(Sx+iSy)/2,S−=(Sx−iSy)/2.Here c is a conventional annihilation fermion,obviously ψ is the Majorana fermion,ψ†=ψ.In fact,the spin-string operator representation of fermions has a geometric implementation in this knot lattice.First,each isolated horizontal loop on a chosen edge is cut and one ending point at the cutting edge of one loop is connected with the ending point of another loop,then the two loops fuse into one.Repeating this operation unites all the horizontal loops into one global loop.Thus the Jordan–Wigner transformation has a natural implementation in this knot lattice model.We require that the flipping operation of the spin operator Sxonly acts on spin states,i.e.,Sx|↑i=|↓i and Sx|↓i=|↑i,to avoid its undefined operation on the crossing of two fermionic strings.

Fig.3.(a)Braiding two anyons of knot state(|↑i+|↓i)twice in clockwise direction.(b)Performing a Majorana fermion operator on the redundant crossing points.(c)Mapping the eigenstate Sxto its eigenstate by braiding.(d)Mapping of the eigenstate Syto its eigenstate by braiding.
Here,the Majorana operator ψ acts on both the crossing of the electric/magnetic current and the two fermionic strings.After the first braiding operation Rm?+e+,two crossings appear in the bottom layer.In order to bring it back to the vacuum state,the Majorana operator could act on either the first crossing or the second crossing to disentangle the two fermionic strings,then perform a Reidemeister move[19]to reach the exact vacuum state of the upper layer(Fig.3(b)).For the|↓i acted on by the braiding operator Rm?+e+twice,two more Majorana fermion operators(ψ1ψ3)have to be performed to map it back to the eigenspace on different crossing points(Fig.3(a)).Thus,the magnetic monopole and positron obey non-Abelian fusion rules in the ground state of the Ising model,[2]

Moreover,the statistical factor of braiding two Ising anyons twice at one lattice site is no longer eiπ;it reads now

Here,i represents the i-th lattice site.The final state after this operation is the first excited state of the ferromagnetic Ising model.The quasi-particle(or kink excitation around a lattice site)on the upper layer is a vacuum-like excitation,while the quasi-particle in the bottom layer is a Majorana fermion pair excitation.If the braiding operation was performed in the counterclockwise direction,the two types of quasi-particles simply exchange their layer levels.Note that the fermionic strings and unpaired Majorana fermion only exist for an odd number of times of braiding(Fig.4).For instance,three clockwise braidings on the eigenstate,(|↑i+|↓i),generate one Majorana fermion and one Majorana fermion pair,

Furthermore, five clockwise braidings generate one Majorana fermion pair ψ1ψ3and a triplet cluster of Majorana fermions ψ1ψ3ψ5(Fig.4).Thus the magnetic monopole and positron fused into a pair of Majorana fermions on the S=+1 sector,and fused into three Majorana fermions on the S=−1 sector.When the Majorana fermion operators act on an even number of crossing sites,the overlapped vacuum state flips its sign.The fusion rule for the magnetic monopole and positron passing through the two fermionic strings which is braided(2n+1)times is as follows:

This fusion rule is a natural output of the multi-knot lattice model,but almost invisible in the conventional Ising model.

Fig.4.The knot configuration after braiding anyons an odd number of times.Here,three and five times of braiding are shown as examples.
2.2.Dual anyon pair in knot lattice model of block spin-1
The knot lattice model for two-state spin,S=±1,does not admit fermionic string state as its eigen-knot state.In fact,the vacuum state generated by the braiding operation can be naturally defined as the spin-zero state(Figs.2(a)and 2(b)),i.e.,Sz=0.The complete Hamiltonian of the knot lattice model includes the long-range coupling along the loop current,

where Sz=(+1,0,−1).If only the nearest-neighbor coupling terms are included,this knot lattice model is reduced to the conventional Ising model of spin-1 spins,

The block spin-1 Ising model is not exactly solved so far.For ferromagnetic coupling Jz<0,the minimal energy state is a magnetically ordered state with spins pointing up collectively or pointing down collectively.However,the Hilbert space is highly enlarged due to the two degenerated spin-zero states.Upon one braiding operation of,the vacuum state and Majorana fermion state can coexist in the Hilbert sub-space with a zero eigen-energy.More braiding operations generate more Majorana fermions in other excited states.The knot configuration of the zero-energy states is made of many entangled loops with different sizes.
Even though the lattice model is confined in two dimensions,the knot configuration is in fact in 3D space.Topological quantum field theory offers a method to calculate the Jones polynomial and partition function of these links.[16]For a chosen common lattice site,i,of the multi-layer knot lattice,the knot configuration of the rest of the lattice sites(except the lattice site i)is first fixed.For each fixed spin state,for instance Szi=0,the partition function(or Feynmann path integral)of this layer could be computed as Z(Szi=0)0,where 0 denotes the ground state.The partition function of Z(Szi=+1)0and Z(Szi=−1)0is obtained following the same procedure.Repeating the same computation on all of the other knot lattice layers of eigenstates leads to the partition function,

where r represents eigen-energy levels.The partition function of the three states satisfy the familiar linear relation in topological quantum field theory and knot theory,[16]
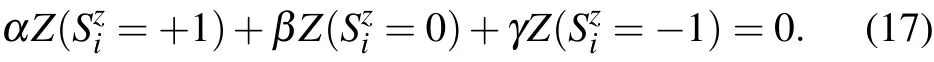
The three coefficients(α,β,γ)in this Skein relation are computable for an explicit knot lattice state.Since the partition function is a topological invariant,the linear combination of them is also a topological invariant.Here the partition function depends on the spin coupling strength and temperature.This topological relation is solid for finite systems.It is convenient for quantum gate manipulations even though it is far from the thermal dynamic limit.The single-spin Hamiltonian,H=hSzi,has four knot states:one over-crossing,two zero crossings,and one under-crossing(Fig.5).The corresponding partition functions with respect to the four knot states are,

The two degenerated zero states are not distinguishable by partition function.The coefficients of the knot invariant Jones polynomial reads,

Here the abstract variable t is a familiar Boltzmann factor in physics.Repeating this Skein recursion relation across the whole knot lattice generates a global knot-invariant polynomial.Then the transition between different crossing states is manipulated by the braid group.The braiding operation can be performed upon the ground state,which has the same bilayer knot configuration as the two-state Ising model.The braiding generates one vacuum and one Majorana state,with both the two spins of the two layers at the i-th lattice flipped to the Szi=0 state.Note that the zero-crossing state has two-fold degeneracy.The Jones polynomial now depends on the external field strength and temperature.Combining the average linking number Eq.(6)with the Skein relation Eq.(17)generates the average linking number for the vacuum state Siz=0 This equation offers one method for computing the average linking number in the spin-zero state as well as that of the spin-up state and spin-down state.It is also useful for exploring topological phase transitions in quantum systems of block spin-1 particles.


Fig.5.The four knot states of single-spin operator Szi.Obviously the two Szi=0 states are not topologically equivalent.
2.3.Electronic anyon states with integral and fractional filling factors in block spin-1 knot lattice model
The knot lattice exposed to a homogeneous external magnetic field demonstrates the same integral and fractional quantum Hall effect.Replacing the magnetic monopole and positron in the knot lattice(Fig.1)with electrons is a natural implementation of 2D electron gas.If a magnetic monopole with magnetic charge Qmis placed at the center of the spherical lattice to exert a magnetic field perpendicular to the knot lattice plane(Fig.6),this electron gas knot lattice shows a similar quantum Hall effect with quantized Hall resistance.The Hall voltage is defined on the four virtual edges in Fig.1.The Hall resistance tensor increases as the magnetic field strength increases.[20]A series of plateaus shows up for certain magnetic field strength,[20]

where ν is the filling factor which counts how many electrons are filled into each magnetic flux quanta.(ν=1,2,...,n)corresponds to the integral quantum Hall effect.ν=n/(2pn±1)leads to the fractional quantum Hall effect.[20]If the electronic current in this knot lattice is either oriented along the horizontal direction or the vertical direction(Fig.1),the off-diagonal terms of the Hall resistance vanish,because electrons have no chance to bend their velocity from the X direction to the Y direction.This kind of knot lattice state only exists for a zero magnetic field,i.e.,the external magnetic charge is Qm=0.A non-zero magnetic field bends the electric current.A finite value of Hall resistance Rxyexists for a knot lattice state with zero-crossing states,i.e.the vacuum knot configuration in Fig.2 and red arcs shown in Fig.6,which are called turning arcs in the following.These turning arcs only appear for an odd number of braiding operations(Fig.4).The output effect of the braiding operator of Eq.(13)is physically equivalent to an effective magnetic field operator,

Wherever one unit of magnetic fieldˆB is applied,the two anyons at the ending points of the electric current are exchanged in a clockwise direction.The inverse operator ofˆB,i.e.,ˆB−1,braids the two anyons in a counterclockwise direction(Fig.2).The three lowest Landau levels of the electron gas in a strong magnetic field can be equivalently mapped into the three quantum states of block spin-1.Only an odd number of braiding times by magnetic field operators upon the state|+1i generates turning arcs in the vacuum state(Fig.2,Fig.3,and Fig.4).The number of crossing points of these entangled turning arcs within one unit cell increases by one for each braiding operation.In order to unknot a pair of entangled arcs with 2n+1 crossing points back to the trivial vacuum state,there must be n Majorana fermion operators acting on the crossing points alternatively.This geometric operation is summarized as the following algebra,
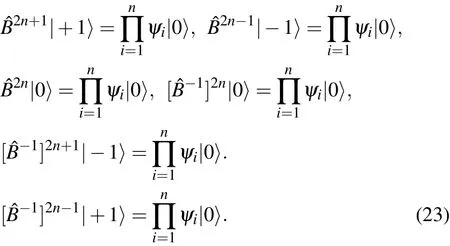
These Majorana fermion operators can be effectively implemented by electrons filled into a magnetic flux bundle which is denoted by the number of operations of the magnetic field operator.Since the magnetic field is homogeneously distributed,all lattice sites are braided simultaneously.The filling factor at one lattice site is the same as for other lattice sites.Then we arrive at the composite fermions attached by the magnetic field.The filling factor for these quasi-particles excited out of vacuum state is the same as that for the fractional quantum Hall system,[20]

Llinkis the linking number.N(ψ)and N(B)are the number of Majorana fermion operators and the number of magnetic field operators,respectively.This is a reasonable physical result,because the two entangled electric currents are equivalent to two solenoids,which generate a magnetic field passing through their interior.These highly entangled knot vacuums are a different implementation of composite fermions.[21]

Fig.6.Electron gas runs through a spherical lattice of knots.A magnetic monopole is placed at the center of this spherical lattice to exert an external magnetic field.The blue circle indicates magnetic flux.The blue triangle and red square indicate the far-separated initial and final anyon,respectively.The red arrow sequence brings the initial anyon to the final location.The blue arrow sequence brings the initial anyon back to its original location.
As for the state transitions from|+1i to|−1i(or vice versa)by a number of braiding operations of the magnetic field operator,it is equivalent to injecting one electric current through the interior center line of the solenoid of the other electric current(Figs.7(a)and 7(b)).The magnetic flux exists by pairs in this case.This state transition can exist at some lattice sites and can be generated from vacuum states which correspond to resistance plateaus similar to the quantum Hall effect.2n number of braiding operations on|+1i generates n Majorana fermions as its eigen-excitation,

and so does the|−1i state.The filling factor for the quasiexcitations from|+1i to|−1i(or vice versa)obeys the following filling factors,
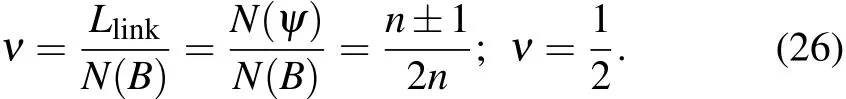
The filling factor in the eigen-energy level of|+1i or|−1i state is ν=n/2n=1/2.One unpaired Majorana fermion maps a|+1i to|−1i(or vice versa).If the total number of Majorana fermions approaches infinity,the fractional filling factor also reaches this half- filling state.However,this unpaired Majorana fermion always exists due to topological braiding.

Fig.7.(a)Two anyons are exchanged within|±1i states with three crossings.(b)The equivalent solenoid helix scheme for the same braiding operation with respect to panel(a).(c)An odd number of many writhing loops generated on square lattice.(d)One writhing loop generated on one arc.(e)The twisted free arcs generated by one braiding.(f)The output of one braiding on the crossing point of the writhing loop leads to one untwisted free arc and one free loop.
The fractional filling factor above only appears for a local knot without self-linking.According to the White formula,[22]the self-linking number is the sum of the twisting number(Tt)and writhing number Ww,i.e.,Slink=Ww+Tt.The writhing number counts the number of loops made by the loop itself(Fig.7(c)),while the twisting number counts the number of twists around its circular column section center(assuming the wire here has finite thickness).The physical implementation of this twisting wire is an electric current generated by a running electron which carries a rotating spin.The twisting number and writhing number can transform into each other,but the sum of the two keeps a conserved self-linking number.Suppose the electric current is twisted during the braiding operation,then this twist would induce the writhing of current and form loops.For instance,there exists a writhing loop on the block square covering four unit squares around local site no.3 in Fig.6.Suppose there are two such writhing loops in a 3×3 block square covering nine unit squares(Fig.7(d)).Applying one braiding on the local crossing point unknots the writhing loop into two different types of free arcs:one is a twisted free arc(Fig.7(d)),the other is an untwisted arc together with a free writhing loop(Fig.7(e)).For the first case,Ww=0,Tt=2,the self-linking number is Slink=2.For the second case,Ww=2,Tt=0,then Slink=2.Thus each twist or each writhing loop is equivalent to one fermion.For a turning arc with many writhing loops or twisting units,it was born together with many fermions.One braiding by the magnetic flux operator is filled with many Majorana fermions(Figs.7(c)and 7(d)).The filling factor for this case demonstrates similar filling factors to the integral and half-integral quantum Hall effect,

The linking number Llink=Ni(ψ)counts the number of Majorana fermion operators to unknot entangled vacuum strings.Ni(B)counts the total number of magnetic field operators.Wwcounts the number of writhing loops.Ttcounts the number of twists.For example,there are two fermions encoded by the writhing loops in Fig.7(d).After two braiding operations B2,it turns into a vacuum state with two crossing points plus the two writhing loops.Then one Majorana fermion must be added to unknot this state,i.e.,Ni(ψ)=1.In total,there are three free fermions in two magnetic fluxes,thus the filling factor is ν=3/2.The writhing number Wwis an independent topological number for counting fermions,Ww=0,1,2,....In mind of the additional twisting numbers on the ending points,the self-linking number could be even or odd.If the total number of fermions is odd,it reaches a half-integral filling factor,ν =n/2.Otherwise,the filling factor is integral ν =n.This integral or half-integral filling factor only exists at the eigen-energy level of the vacuum state,|+1i and|−1i.The quasi-particle excited out of these eigenstates obeys similar fractional filling factor equations[Eq.(24)or Eq.(26)]by replacing N(ψ)with(N(ψ)+Ww+Tt).The braiding algebra is independent of space scale,thus it is quite robust under renormalization.For example,if the two free turning arcs in the vacuum state generate writhing loops in the same way,then the total writhing number is an even serial,Ww=0,2,4,6,....If the twisting number is zero,the even writhing number leads to the half- filling serial for filling factors in eigen-energy levels,ν=(2n+1)/2.For the quasi-particle or quasi-holes excited out of the vacuum,an even writhing number generates ν=(n+Ww)/(2n±1).For instance,n=1 leads to the serial,ν=(n+Ww)/(2n+1)=1/3,1,5/3,7/3,3,....n=2 leads to the serial,ν=(n+Ww)/(2n−1)=2/3,4/3,8/3,10/3,4,....An odd number of writhing loops only exists for the case that the two turning arcs generate different numbers of writhing loops.The linking number of the crossing current within one unit square could be equivalently viewed as the writhing number of a larger current crossing covering many unit squares.This equivalence induced one-to-one mapping between the integral filling factor and fractional filling factors.This knot lattice model offers a topological explanation to Jain’s composite fermion theory.
If the external magnetic field distribution is not homogeneous but has a fluctuating strength distribution within the scale of a few lattice sites,the filling factor would be more continuous.Even though it is quite hard to confine a magnetic field in a nanoscale circle,inhomogeneous doping of magnetic particles still provides a possible way. In this case, the crossing states in different block squares would be acted on by different times of braiding operators at the same time and generate Majorana fermions at different locations simultaneously.In that case,the renormalized filling factor is computed by direct summations,

The linking number is Llink=Ni(ψ).These filling factors are mostly likely shown as plateaus in Hall resistance,but fit in the continuous straight lines.The writhing free loop in the counting above is equivalent to free fermions,while the free loop without self-crossing is simply a vacuum.It takes four fermionic turning arcs to form a vacuum loop.Thus the vacuum loop behaves as a boson.An even number of electrons is trapped in the vacuum loop and cannot move freely in the whole space.If the whole lattice is covered by free vacuum loops without any exception point,the total linking number of this insulating state is zero.The Hall resistance of this insulating phase depends on the oddness or evenness of the length of the virtual edge.If the total number of columns is even,then the local in-and out-current pair cancel each other to reach a zero Hall current.If the total number of columns is odd,there always exists one unpaired in- or out-current on the edge.Thus the Hall conductance has an odd–even dependence on the finite size of the lattice.
The quantum Hall effect for the knot lattice model of electrons is intrinsically originated from the Chern–Simons field theory:the non-Abelian Chern–Simons action is a topological invariant of many entangled knots,[16]while the Abelian Chern–Simons theory determines the topologically quantized Hall resistance in the fractional quantum Hall effect.[23]Here the Hamiltonian of electrons moving along the tangential vector of the horizontal loop or vertical loop can be formulated as the same for quantum Hall systems,[20]

where the potential termV=Vi+Vij+V(S).Vi=e2/dε is the on-site repulsive interaction at each over-crossing point with d the distance between the upper current and lower current.Vijis the column interaction between electrons.Since the on-site distance between electrons is much smaller than the distance between electrons at different lattice sites,then Vi?Vij.The on-site repulsion prevents two electric currents from touching each other,which results in knot current.V(S)indicates the interaction between the twisting spin 1 of the composite electron and magnetic field,which encodes the topological filling factors of the quantum Hall effect.The gauge field vectors,Ai,xand Ai,y,are induced by the magnetic field and obey a symmetric gauge(Ai,x=eBy/2,Ai,y=eBx/2).Since electrons are still moving in continuous channels,the continuous Hamiltonian theory for fractional quantum Hall effect also works here.Note here that the on-site repulsion potential Vihas periodical distribution.acsis the Chern–Simons gauge field.2p flux quanta is attached to the electron under Chern–Simons transformation.In the knot lattice model,each ending point is attached by a flux quanta assigned by the Chern–Simons field.The collective wave function of electron currents in the knot lattice can be described by an extended Laughlin wave function,

zi,arepresents the coordinates of the four ending points at the middle point of the edge of the unit square,which is the ending point of two crossing strings.Here a=|0i represents the vacuum state.b=|−1i or b=|+1i represent the spin-up state or spin-down state.This Laughlin wave function indicates that two fermionic strings in the same unit square cell obey fractional statistics.The composite fermions in different unit square cells also obey fractional statistics.For instance,suppose the ending point at the i-th unit cell(the blue square in Fig.6)exchanges its position with one point in the j-th unit cell(the red triangle in Fig.6).It takes three braidings to bring the blue square to the position of the red triangle,but it takes only two inverse braidings to bring the red triangle to the home of the blue square(Fig.6).As a result,there is only one braiding survived at the j-th unit cell.Thus,braiding two fermions in different unit cells obeys the same statistics as that within one unit cell.
The collective wave function of other filling factors can be constructed by Jain’s composite fermions theory,[21]since these electrons are always running in a closed loop which bears non-zero vorticity.Each loop of electric current also generates a magnetic field.The Abelian Chern–Simons action counts the total helicity of these entangled knots.When the knot configuration fluctuates from one pattern to another,some knots inevitably will be cut and reunite,which induces some opposite magnetic fields against the external magnetic field due to Lenz’s law in electromagnetism theory.Thus the fractional quantum Hall effect can still exist in this knot lattice model even if there is no external magnetic field.In that case,the total phase flux in different sub-lattices must cancel each other.
2.4.Anyons in long-range hopping insulator model and quantum spin Hall model on square knot lattice
The presence of the magnetic field in the square knot lattice breaks the time reversal symmetry.Without the external magnetic field but introducing spin–orbital coupling into the Hamiltonian results in the quantum anomalous Hall effect.[23]The knot configurations provide a geometric representation of the fermion filling states of the anomalous Hall Hamiltonian.On the square knot lattice in Fig.1,we define the crossing state that the blue wire is below the black wire as the zero filling state of the fermionic operator,i.e.,|0i=|S=−1i.The output of annihilation fermion operator cion|0i is zero.The creation fermion operator,c†i,generates one fermion out of the zero filling state,c†i|0i=|1i.The one-fermion state is defined as the opposite crossing state of|0i,i.e.,|1i=|S=+1i(Fig.1(e)).For a spinless particle,the Pauli principal forbids the existence of two fermions at the same site,thus c†ic†i|1i=0.The annihilation operator brings the one-fermion state to a vacuum,ci|1i=|0i.If the fermions bear an intrinsic spin state,each current at the crossing point has to be oriented as the four crossing states(Fig.1(e))to match the coupling between the different spin states.We first focus on spinless fermions in the following.One long-range fermion hopping model on the knot lattice model in Figs.1(a)and 1(b)can be constructed as
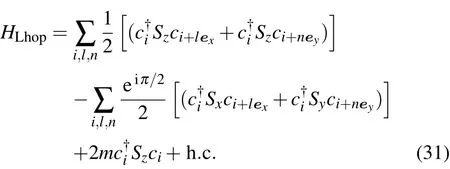
The spin-1/2 operators(Sx,Sy,and Sz)are global spin operators which couple to the horizontal(or vertical)fermion current.The Fourier transformation of fermion operators on this knot lattice is naturally anisotropic,

This two-band topological insulator model reduces to the diagonal Hamiltonian in momentum space,

For the nearest-neighbor coupling case,this knot lattice model naturally reduces to a conventional topological insulator model,[24]
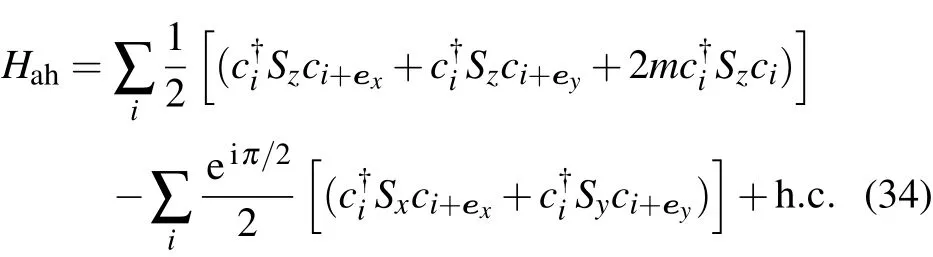
Non-zero Chern numbers exist for the energy spectrum with respect to different polarization degrees.[24]The Chern number in momentum space is not solely determined by the real space topology,since the same knot configuration acted on by different Hamiltonians maps out different energy spectrums.Different Hamiltonians organize the knot lattice layers in different ways.However,topological physics in real space are still encoded in momentum space.The linking number is defined as the total number of positive crossings minus the total number of negative crossings.Here,the negative crossing is represented by the zero filling state,ni=c†ici=0.The positive crossing is counted by the one-fermion filling state,ni=1.Thus the linking number in this fermion–spin coupling model is in fact the total number of fermions,

The total number of fermions is a topological number in this knot square lattice.The diagonal electronic conductance of this knot lattice model is quantized by the number of unbroken channels in the X direction or Y direction.The global spin component Sxis coupled to running fermions in X loops∑ksin(kx)nkx.Syis coupled to running fermions in Y loops∑ksin(ky)nky.However,the Szcomponent is not only coupled to the on-site occupation,but also coupled to the fermion current in X andY loops.As long as the fermion numbers in X or Y loops are not zero,they will contribute to the Szcomponent.
The real-space Hamiltonian equation(34)assigned a spin Szcomponent on each crossing point.The loop currents along the X direction carry Sx.The loop currents along the Y direction carry Sy.The evolution of each spin component is governed by the Heisenberg equation,

In the continuum limit,the right-hand side of Eq.(36)is equivalent to Rashba spin–orbital coupling.For a constant polarization∂tSz=0,then∑kxsin(kx)nkxhSyi=∑kysin(ky)nkyhSxi.In the classical representation of spin,Sxcan be expressed as the projection of a total spin,

Then the stable configuration of spin components obeys equation,

The orientation of spin in plane is labeled by the projection angle θ.Obviously hSyi increases when hSxi decreases.In order to fulfill the balance Eq.(38),the total number of fermions in X loops has to be reduced;in the meantime,the total number of fermions in the Y loop must increase.Since the total fermion number is a conserved number,there must exist turning arcs in the knot square lattice to fuse the X loop into the Y loop,driving the fermions from the X loop into the Y loop.In this sense,the output effect of spin–orbital coupling is equivalent to an external magnetic field.Since the global spin performs the same action at every lattice site,the turning arc shows up around every lattice site.
The Hall conductance of this two-band model is quantized by the first Chern number in momentum space.[24]As we all know,the energy function derived in the real-space model is exactly the same as its equivalent model in momentum space,even though sometimes it is quite difficult to get the formulation of the energy spectrum in real space.Fourier transformation does not change the intrinsic topology of the energy manifold,except for a coordination transformation from the space index into the wave vector index.The momentum space is the reciprocal space of real space.However,the wave vector in the thermal dynamic limit turns into a continuum variable,while the space index for the Hamiltonian in real space is still discrete.Next,we consider a finite system with finite particle number and lattice size.A knot in real space can still map into a knot in momentum space;maybe it is expressed in different geometries,but its topology should remain the same.As an explicit example to support the above conjecture,we study the extremely simple case that both the fermion occupation in the X loop and Y loop are single occupied,nkx=nky=1.For a general consideration,the lattice constant axin the X loop is controlled at a different value from that of the Y loops,i.e.,ax6=ay.A vector in real space,R=nxax+nyayis a dual vector of the reciprocal vector in momentum space,K=kxbx+kyby,here(bx=2π/ax,by=2π/ay).The two dual vectors obey the unit relation,ai·bj=2πδij.The coupling current of the three spin components are listed as follows:
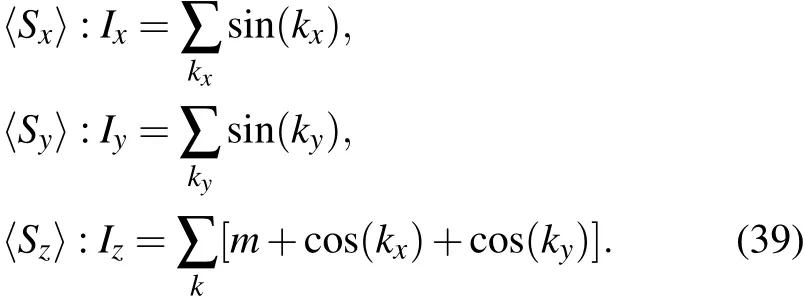
In order to encode the lattice constants into the equations above,we reformulate the wave vector components as

where ω is the spatial oscillation frequency of the current defined by(ωx=1/ax, ωy=1/ay),which counts the lattice length covered by one wavelength.For a general consideration,a phase factor φiis introduced into each current,then the three coupling fermion currents read,

The three current functions above define a Fourier knot in momentum space.[25]One familiar example of Fourier knots for physicists is Lissajous knots,[26]which are usually visualized by an oscilloscope.Inputting two sinusoidal electric currents into the vertical and horizontal channels at the same time,the oscilloscope displays different closed loops with respect to the different frequency ratios.
The Fourier knot is not always a closed knot.A closed knot only appears if the wavelength ratio(ωx:ωy)is a rational number.For instance,if(ωx:ωy=1:1,φx= φx=0),the Lissajous curve is a circle and projects a straight line in the kx−kyplane.The knot for ωx:ωy=1:2 is a wave circle in three dimensions but projects a∞shape in the kx−kyplane(Fig.8).For a higher number of ratios,the Lissajous knot demonstrates more fluctuations(Fig.8).The Fourier knot configuration of the original fermion current Iiis independent of the value of polarization m.Different m simply shift the whole knot upward or downward.However,this is not the case for a normalized fermion current.

Fig.8.The Lissajous knots in momentum space for original fermion current Iiwith different frequency ratios ωx:ωy.
The topological Chern number is defined by normalized fermion current in momentum space.[17,24]Here we choose a formulation of three fermion currents similar to Ref.[24]for simplicity but with adjustable frequency,(Ix=sin(ωxk),Iy=sin(ωyk),Iz=[m+cos(ωxk)+cos(ωyk)]),then use the total energy spectrum
to normalize the fermion currents,

This normal fermion current also demonstrates 3D knots in momentum space.We first study the special case,ωx:ωy=1:1.The knot configuration shows different geometries with respect to the different polarization degree m.For m=0,it is two parallel lines instead of a closed loop.For 0 The normal fermion current for other frequency ratios shows more fluctuating knots in momentum space.Different values of magnetization m classify the knots or unknots into different zones.For m=0,there only exist parabola curves instead of closed loops.For most cases,the total number of these parabola curves equals the sum of the two frequency numbers.As shown in Fig.9,there are two branches for ωx:ωy=1:1,three branches for 1:2,and five branches for 1:4.However,this rule does not hold for all cases;there are only two branches for 1:3,six branches for 3:5,and ten branches for 5:7,but only twelve branches for 7:9.The physical reason for this serial is not fully understand yet.However,the output of extremely high frequency ratios is the same,and it all leads to two separated bands with different edge branches(in Fig.9,1:100,m=0). Fig.9.The Lissajous knots in momentum space for normalized fermion current niwith different frequency ratios ωx:ωyand magnetization degree m. The Lissajous curves for a magnetization m<3.5 are always a collection of parabola curves for arbitrary frequency ratio ωx:ωy.For example,the output curve of ωx:ωy=1:2 with m=2 is two upward parabola curves with double wells,which turn into downward parabola curves for m=−2(Fig.9),while the ratio 1:3 with m=2 generates one parabola curve with three wraps(Fig.9). ωx:ωy=1:6 results in four deformed upward parabola curves(Fig.9).The high frequency ratio with m=2 finally converges to a cup-like network with four touching points on the bottom(Fig.9,1:100,m=2). The closed Lissajous knot only exists for m>3.5.The 1:1 case is a loop without self-writhing loops,while 1:2 and 1:3 generate a loop with two writhing loops and three writhing loops,respectively(Fig.9).For high magnetization m=40,the Lissajous knot forms a tent-like knot with many writing loops(Fig.10),3:7,m=40),which turns into a tent-like network cage,as shown by the case of 3:100,m=4(Fig.10).These Lissajous knots approach the tent-like parabola network for high magnetization m→∞;one example is shown in Fig.9,1:1,m=100. The topological quantum field theory of the non-Abelian Chern–Simons action provides a topological invariant for many entangled knots,while the Fourier knot is only a special case of a general link with many entangled knots.Thus we could introduce the Chern–Simons action[16,17]to quantify the Fourier knots here.Another topological invariant for the collection of all of these knots is partition function.The partition function for knots in real space shares the same formulation as that for knots in momentum space.These topological invariants are globally topological invariants,and sometimes the local topological invariant for a special eigenstate is really relevant to experimental measurement.For instance,the ground state and the first excited state are of most concern for physicists.For any knot configuration of ground state,the Euler number is always a topological invariant.The Euler number of a closed curve which is homotopic to a circle is always zero.The Euler characteristic number for a continuous closed curve can be computed by Morse theorem.For a given knot in momentum space,there always exist some critical points at which the fermion current satisfies∂ksns=0.For instance,the∞-shaped knot in the kx−kyplane(Fig.8)has six critical points.The local curve of two critical points on the upper boundary is approximated by n(kx)=−ak2x,and n(kx)=ak2xis for two points on the bottom boundary.The critical point on the left boundary is n(ky)=bk2y,and n(ky)=−bk2yfor the right one.Then the Euler characteristic number is computed by the Morse theorem,[27] q is an index counting the independent directions in which the current decreases.For the∞shaped knot,there are two points with q=1 above,two points with q=0 on the bottom,one q=0 for the left boundary,and one q=1 for the right boundary.cqcounts the total number of points with index q.The Euler characteristic number of this∞shaped knot is χ =(−1)03+(−1)13=0.For the Lissajous knot,the number of critical points of the horizontal critical point to that of the vertical point is directly readable by the frequency ratio on the oscilloscope,cxq:cyq=ωx:ωy.For the magnetization m>3.5 or m<−3.5,the fermion currents are closed curves,thus the Euler number is zero. Fig.10.The energy spectrum E(k)with respect to different frequency ratios and magnetization value m.The bottom row shows the Lissajous knots of normalized fermion current nifor large frequency ratios ωx:ωy,i.e.,(3:7,3:100). The fermion current for the other two cases is not homotopic to knots anymore.In that case,the Euler–Poincare equation is more effective for computing the topological numbers,[27] where bqis the Betti number,which counts the number of the q-dimensional simplex.For instance,the 0-dimensional simplex is a point.A 1-dimensional simplex is a line segment.A 2-dimensional simplex is a 2D surface.For the zero magnetization case,m=0,the fermion current in different frequency ratios is composed of curves.In that case,these curves approach a parabola curve for an infinite wave vec-tor.For this knot lattice system,the momentum wave vectors have a cut-off at the unit lattice space,kx=1/axand ky=1/ay.In that case,there always exist two ending points(b0=2)and one line(b1=1)for each branch,thus the Euler number is χ =(−1)02+(−1)11=1.This Euler number has the same value for the parameter range,0 The energy spectrum shows that closed knots in momentum space only exist for a gapped two-band model(Fig.10).If the two bands form a periodic closed spectrum loop,its corresponding current knot in momentum space is a collection of parabolas with double wells.The two bands intersect each other for zero magnetization m=0.The corresponding current knot is a pair of separated flat branches.For a larger magnetization m=40,the two bands in the spectrum become almost flat with a fine wavy structure,which is induced by the interference between the waves with two frequencies,3 and 7.A reversed magnetization induces a phase flip of the spectrum wave.In the meantime,the corresponding knot in momentum space switches to an opposite direction.For a larger frequency ratio,3:100,the spectrum wave becomes a modulated composite wave with many fine waves in each macroscopic wave section(Fig.10),and the corresponding knot in momentum space is a tent-like network(Fig.10).For a finite lattice,there exists a gapless edge state on the boundary. The topological insulator model only considers the coupling between the orbital of a spinless fermion and a global spin operator.[24]Thus the knot square lattice implementation of the topological insulator model only incorporates undirected fermion current in the X and Y loops. The j0i state is defined as vertical current above horizontal current,while the opposite setup defines|1i.The spin-up and spin-down fermions have a natural implementation by directed fermion currents in the knot lattice.For charged spin fermions in the loop channel,an electric field confined in the x–y plane could induce the quantum spin Hall effect.[28]Here,the electric field is oriented along the the y-axis to drive electrons running in the Y loops.Then the spin-up state|↑0i is defined as a state where the positive Y current is above the X current,|↑0i corresponds to the Y current being below the X current(Fig.11(a)).The negative Y current defines the spin-down states correspondingly(Fig.11).The direction of spin is perpendicular to the electric current and electric field,following the equation Jij= σsεijkEk.The action of spin fermion operators obeys the following rules,c†↑|↑ 0i=|↑ 1i,c†↑|↑ 1i=0,c↑|↑ 1i=|↑ 0i,c↑|↑ 0i=0.The operation of the spin-down fermion operator follows similar rules.The effective Hamiltonian for this spin Hall system is composed of two topological insulator models,Eq.(34),but incorporates an opposite Y current, Here the Hamiltonian Hs(k)shares the same formulation as the topological insulator model Hamiltonian Eq.(33)in momentum space.This Hamiltonian reduces to the effective Hamiltonian of the quantum spin Hall insulator near the Γ point.[29]The spin Hall current also turns from the Y loop into the X loop due to the spin–orbital coupling interaction(Fig.11(a)).The gapless edge current runs along the edge without dissipation.The spin current on the upper edge carries the opposite spin and runs in the opposite direction to that of the spin current on the bottom edge(Fig.11(b)),and so does the left edge and right edge.However,if the number of Y loops is an odd number,the spin current on the left edge runs in the same direction as the spin current on the right edge that carries the same oriented spins(Fig.11(b)). Fig.11.(a)The four crossing states with respect to different spin states.The red arrow indicates spin.(b)The spin current on the edge with even number ofY channels.(c)The spin current on the edge with odd number of Y channels. The anyon current model above only considered continuous current without any local confliction.If we consider the conflicting patterns of directed anyon current at each local crossing point,this knot lattice model demonstrates topological fermion pairing phenomena.For the nearest-neighbor hopping case,the knot lattice model reproduces a similar momentum pairing Hamiltonian with respect to the well-known Bardeen–Cooper–Schrieffer(BCS)fermion pairing model for the conventional superconductor.[30]Electrons with opposite spin and momentum are coupled into pairs as the main carrier of superconductor current.If we only consider the pairing pattern between the nearest-neighbor crossing sites,the self consistent construction of fermion pairing in the knot square lattice has only two possible configurations(Fig.12(a)).An alternative distribution of the|+1i and|−1i crossing states constructs one stable fermion pairing state.Flipping|+1i to|−1i(or vice versa)on the whole lattice is another equivalent pairing state(Fig.12(a)).Thus the fermion pairing on the knot square lattice has two-fold degeneracy.The fermion pairing Hamiltonian in the 2D bulk area reads, The Fourier transformation of fermions has separate wave vectors in the X loops andY loops correspondingly, and Substituting this Fourier transformation into the Hamiltonian Eq.(46)in real space leads to This Hamiltonian bears the same structure as the BCS Hamiltonian in momentum space.Following the usual mean- field approach,we define the same energy gap function for exciting a Cooper pairing,∆ =∑kVhckc−ki.Usually this energy gap is a complex function,∆ = ∆1+i∆2,∆∗= ∆1−i∆2.The bulk pairing Hamiltonian can be formulated as a fermion spinor ψ†k=[c†k,c−k]Tcoupled to a pseudo-spin vector,σ, Here I is a 2×2 unit matrix.Sxand Syare conventional Pauli matrices.For different pairing states,[30]this pairing Hamiltonian defines different Fourier knots in momentum space.For instance,the p-wave pairing gap function defines a typical Fourier knot,[25] However,here there is no σzcomponent.Thus the pairing gap function defines 2D Lissajous curves in momentum space.The fermion pairing state here is in fact a single plaquette state in each unit square.It is an antiferromagnetic order state for the block Ising spin|+1i and|−1i(Fig.12(a))in real space.The self-consistent pairing state is the two-fold degenerated ground state of the Ising Hamiltonian for coupling block spin,Hpair=JSz iSzj,with J>0.The eigenstate of Sziis the blockspin states shown in Fig.12(a).Two neighboring unit squares with the same block spin cannot match each other self-consistently.Two fermions with opposite spins would collide with each other on the square boundary where no channel exists for them to continue the current without turning back.Inside each unit square,the two incoming fermions of the X loop could tunnel up into the Y channel and split up to fit into the continuous current loops without frustration.This convective fermion current actually conserves the total number of fermions(Fig.12(b).The tunneling current from bottom current to upper current is also a fermion pairing Hamiltonian, where the bottom current(upper current)is denoted by b(u).A normal state is not a fermion pairing state,and the local crossing state may be randomly distributed over the whole lattice.Then we have to use a multi-layer knot lattice to represent the superposition of quantum states.For a periodically located multi-layer knot lattice,the pairing Hamiltonian Hbzulkmaps onto four-fermion interaction in momentum space by Fourier transformation.Because the fermion pair only moves upward along the Z-axis,the time-reversal symmetry is broken.The tunneling Hamiltonian under mean- field approximations reads, Here,denotes the average occupation number difference between the positive wave vector and negative wave vector.Because only the fermion moving to the positive Z-axis reduces energy,an oppositely moving fermion would increase the total energy.In order to match the formulation of Hamiltonian Eq.(47),we replace k with−k in the fermion operator ck,↓.Since the spin-up and spin-down move upward together as a pair,n↑(k0)should have the same occupation as n↓(k0).The Hamiltonian for Z current reduces to a brief formulation, Szis the Pauli matrices. Then the total Hamiltonian of fermion pairing is a 3D spin-coupled to fermions, Hbulk(k)=ψ†k[εkI −∆1Sx+∆2Sy+∆N(k)Sz]ψk.(53) The gap function and the occupation number together define a Fourier knot in 3D momentum space, I =[Ix=∆1,Iy=∆2,Iz=∆N].The energy spectrum of this mean- field Hamiltonian isFollowing Duan’s topological current theory of the magnetic monopole,[31]a topological particle sits at the singular point of the normalized energy current,The topological current of the magnetic monopole is Here, εijlis the Levicivita symbol, εijl= −εjil. Nontrivial topological particles exist in the gapless mode,i.e., In this fermion pairing model,the gapless points are located along a centerline passing through the center of a string of vortices in momentum space.However,this topological vortex is also visible in real space on a knot square lattice.The complete vortex only exists in the bulk area,while a half-vortex and a quarter-vortex could both exist in the bulk and edges. Fig.12.(a)The two different fermion pairings with respect to two crossing states,and the corresponding four vacuum states.(b)The crossing currents as a projection of the two edges of the Mobius strip.(c)The spin current on the edge of the pairing square lattice with an even number of Y channels.(d)The spin current on the edge of the pairing square lattice with an odd number of Y channels. The fermion current of unpaired fermions running on one edge is always in the opposite direction to its opposite edge.The edge current in this fermion pairing model does not show the same odd–even effect as that in spin Hall current.For an even number of Y loops,the spin of the fermion flips sign when the Y current enters its neighboring opposite Y current(Fig.12(b)),but keeps the same orientation of electric field, E/|E|=( J × s )/|J||s|,where J is the fermion current vector,and s is the spin vector.Meanwhile,for an odd number of Y loops,the Y current fuses into X current by flipping the orientation of spins in a certain way so that the electric orientation also flips(Fig.12(c)),i.e., E →− E.The effective Hamiltonian of the edge current for both the two cases reads, The equivalent Hamiltonian in momentum space is Hedge=2tijsin(kx)c†kx↓ckx↑,which reduces to a gapless dispersion near kx→0.The edge current on the upper boundary moves to the opposite direction of the bottom current,as does the left edge current and right edge current.This phenomenon holds both for an even number and odd number of Y loops(Figs.12(b)and 12(c)). The global pairing state has only two consistent patterns which place the two local pairing patterns alternatively on the whole lattice;any local flipping of one block spin results in contradiction.However,if one block spin of current crossing is braided into a vacuum state,the rest of the pairing states can still exist consistently.In other words,breaking a local Cooper pair on one lattice does not destroy the super-conducting states on other lattice sites.For the block spin state|+1i,there are two braiding operators to break the Cooper pair.One is counterclockwise braiding which turns an angle of π/4 away from the X loop,which is denoted as Bt?(Fig.12(a)).It results in a vacuum state with positive chirality following the righthand rule,|+0i.The other braiding operator turns an angle of 3π/4 away from the X loop,which we denote as Bn?.This clockwise braiding disentangles the crossing of pairing current into a vacuum state with negative chirality,|−0i.The clockwise braiding Bt?turns|−1i into a negative vacuum state|−0i,while counterclockwise braiding Bn?braids|−1i into a positive vacuum state|+0i.Four neighboring vacuum states with the same chirality can form a minimal loop.Electrons run through this minimal loop to go around a magnetic flux(Fig.13(a)).Each minimal loop represents a vortex in a superconductor.This knot square lattice for the fermion pairing pattern is equivalent to the overlap of two square sub-lattices,denoted by the black discs and white circles respectively in Fig.13(a).These two sub-lattices are the dual lattice of the unit cell,on which the magnetic fluxes with opposite chirality are distributed.A negative chiral vortex around a negative flux only exists at the black sites,while positive vortices only sit on the white sites.Each flux site is surrounded by four unit cells.Since each braiding over a unit cell only generates two arcs with the same chirality,opposite vortex loops cannot coexist as nearest neighbors.However,a vacuum current can separate two vortex loops to prevent them from annihilation(Fig.13(a)). Fig.13.(a)Vortices with opposite chirality locate on different square sublattices.The vacuum vortex lines entangle with other vacuum arcs.(b)The unoriented Seifert surface for fermion pairing state. Each vortex loop confines two electrons.One electron vanishes from the unit cell at site(i,j)and is generated at site(i−1,j−1);this process only draws a half-circle.In the meantime,another electron must annihilate at(i−1,j−1)and generate at(i,j).The fermion pair current is topologically quantized.The complete vortex loop carries an integral winding number W=±1,while the half-vortex loop carries a half winding number W=±1/2.A quarter-arc carries a fractional winding number,W=±1/4.The complete vortex loop carries two electric charges.A quarter-arc has only half-charge,e/2.If more braiding operations are performed over the two vacuum arcs within one unit cell,the vortex would entangle with the super-current of the fermion pair,or two vortex lines may also entangle each other(Fig.13(a)).This non-trivial entanglement is characterized by linking number.Helicity is an effective topological quantity of entangled vortex lines, where Jis the familiar super-current of fermion pairs, where∆is the gap function for fermion pairs.Since the Cooper pair is a composite boson of an electron pair with opposite spins,∆is also a bosonic operator after the second quantization.ˆD=∇+i2πφ0is the covariant derivative.The spin of the electron flips by the accumulated phase factor of the magnetic flux(Fig.12(a)),φ0=HAdl=R∇×Adx2=RBdx2.The helicity equation(56)is actually equivalent to the Abelian Chern–Simons action,which is the topological number of many knots.[17]If there are 2N crossing points between the vortex lines over the whole vortex lattice,it takes N Majorana fermions to bring an entangled vacuum state to a free vortex state.Similar to the fractional quantum Hall state,the fractional filling state also exists for two entangled vortices in a superconductor. Besides the linking number of entangled knots,the Euler characteristic is also an effective topological characterization of the knot square lattice of the fermion pairing model.The Euler characteristic for an oriented,connected compact surface is χ(S)=2(1−g),where g is the number of genuses(holes).It is in fact the first Chern number.The Seifert surface has to be constructed in order to compute the Chern number of a knot.For an arbitrary knot,Seifert’s algorithm first colors the projected plaquette alternatively into a checkerboard state,then lifts up the plaquette with the same color and views the plaquette with opposite color as a hole.At each crossing point,each in-arrow must connect to its nearest-neighboring out-arrow.Then the knot is decomposed into oriented loops.Filling these loops with color to generate a disk and then connecting them by a twisted Mobius strip whose boundary projects the original crossing states in the 2D plane creates the so-called Seifert surface.[32]To apply the Seifert algorithm on this knot square lattice,we first choose the plaquette on the white sub-lattice as the filled surface(represented by the green spherical surface),while those on the black sub-lattice are holes(represented by the white blank zone in Fig.13(b)).Then we connect the in-arrow to the out-arrow at every crossing site.It finally reduces to periodically distributed vortex loops(the green spheres in Fig.12(b)).We fill these loops and connect them by a Mobius strip in such a way that the original current crossings are the projection of the two edges of the Mobius strip(Fig.12(b)),which are represented by the green belt that connects two green spheres in Fig.13(b).Then the knot square lattice of pairing states maps into a lattice of periodically distributed Mobius strips(Fig.13(b)).However,this Seifert surface is still not an oriented manifold due to the opposite arrows of fermion pairing in this special model.In order to construct a closed current loop,we introduce two more currents that connect the two in-arrows to the two out-arrows in the middle waist of the Mobius strip(Fig.12(b)).Then it leads to an oriented current network on an unoriented Seifert surface.In fact,the Euler characteristic for this case cannot distinguish an oriented surface from an unoriented one.The Seifert surface in Fig.13(b)has a Euler characteristic of χ=2(1−5)=−8,since it has five genuses.For a square lattice with(2N+1)×(2N+1)unit squares,the total number of genuses is g=[(2N+1)2+1]/2.The corresponding Euler characteristic is χ =1−(2N+1)2. The Euler characteristic is an effective topological number for classifying different fermion pairing patterns on a square lattice.The ferromagnetic ordering of current crossing is the minimal self-consistent lattice model for fermion pairings.Strip ordering and ferromagnetic ordering could show up if a local crossing flips under thermal fluctuation.In that case,two out-arrows (or in-arrows) may collide on the boundary of a unit cell,on which there is no outgoing current existing.In order to construct self-consistent continuous current loops,extra current perpendicular to the two out-arrows on the boundary has to be introduced(the red arrows in Figs.14(b),14(c),and 14(d)).For the ferromagnetic order state, each one of the original four unit cells is divided into four small unit cells with halflattice constant(Figs.14(c)and 14(d)).Thus the total number of unit cells increased to 16.While the current of strip ordering on the boundary between|+1i and|−1i is consistent,any extra current would result in contradiction(Fig.14(b)).Thus extra current is only introduced on the boundary between|+1i and|+1i(or|−1i and|−1i)(Fig.14(b)).The corresponding 2D surface with respect to different ordering states can also be constructed following the Seifert algorithm.The Seifert surface of a(2N+1)×(2N+1)knot square lattice has a Euler characteristic χ =1−(2N+1)2genus,while this to po-logical number increases to χ =1−4(2N+1)2for a homogeneous ferromagnetic ordering state.The strip ordering has an intermediate Euler characteristic number.The ferromagnetic ordering of current crossing in real space can actually be mapped onto separated current loops by Reidemeister moves,while the antiferromagnetic ordering of current crossing requires the maximal number of flipping operations on certain crossing points to map it into separated loops.The total number of flipping operations to map many entangled knots into free loops can be used to quantify the topological entanglement of a link.In this sense,the antiferromagnetic ordering of block spin for fermion pairing has the maximal topological entanglement.Thus a superconductor should have maximal topological entanglement. Fig.14.(a)The current crossing states for antiferromagnetic ordering,|ψi=|↑↓↑↓↑↓ ···i.(b)The current crossing states for strip ordering,|ψi=|↑↑↑ ···↓↓↓i.(c)and(d)The current crossing states for ferromagnetic ordering,|ψi=|↓↓↓↓ ···i and|ψi=|↑↑↑↑ ···i. The Seifert surface provides mathematical mapping of a knot square lattice into a 2D surface with genus. If we consider the physical implementation of the Seifert algorithm,the filled plaquette is physically implemented by a magnetic flux in the vortex loops.The connection of an in-arrow to an out-arrow is physically implementable by a local braiding operation on each crossing point,which can be realized by a physical magnetic field in the plane.However,in this knot square lattice,the filled vortex loop cannot connect to its four neighbors at the same time to construct a 2D surface with many holes.A vortex either exists as an isolated loop or connects only to one of its four nearest neighbors to construct a dimerized lattice of vortex pairs(Fig.15).Only vortices with the same chirality can form a dimer by coupling to the crossing super-currents(Figs.15(a)and 15(c))or vacuum state(Fig.15(b)).Different dimer lattices have different Euler characteristic numbers.We make an inverse filling of the Seifert surface of the dimer lattice.Then each filled vortex loop becomes a hole of the continuous surface.For a lattice with 2N×2N unit cells,there exist N2isolated vortex loops,and N2/2 possible vortex dimers.The Euler characteristic of the isolated vortex lattice is χ =2(1−N2).The vacuum vortex dimer phase has a Euler characteristic χ =2(1−N2/2),as does the positive and negative vortex dimer phase.The Euler characteristic cannot distinguish a Mobius hole from a trivial hole. Fig.15.(a)The dimer lattice of negative vortex pairs.(b)The dimer lattice of vortex pair coupled to vacuum.(c)The dimer lattice of positive vortex pairs. These vortex loops behave as fermions in the vortex dimer lattice,which is originated from the fermionic string arc in this knot lattice model.Each fermionic string arc can be represented by a Grassmann number.The Grassmann number obeys the following algebra,ηiηj= −ηjηi,ηiηi=0.We place a Grassmann number,ηi,at the center of each vortex loop.These vortex loops are regularly distributed on the square lattice.For a dimer lattice of the same chiral vortex loops,the total number of all different covering patterns can be computed by the Kasteleyn matrix,[33]which is equivalent to the square root of the determinant of quadratic fermion action,S= ∑i Note here that the vacuum vortex dimer admits a self consistent coexistence with the positive vortex dimer or negative vortex dimer.But the positive vortex dimer and negative vortex dimer cannot perfectly coexist without introducing geometric frustrations(Fig.13(a)).The effective action for vortex dimers on the square lattice bears the same formulation as classical dimers[34]but with rotated wave vectors, This effective action holds for a lattice covered by pure dimers.If we consider the hybrid dimer lattice covered by a positive vortex dimer and a vacuum vortex dimer(or a negative vortex dimer and vacuum dimer)together,then the total number of all possible covering patterns is the product of two equal partition functions for pure dimers,Z2.In that case,the effective action for the vortex dimer lattice is The gap closing points are periodically distributed in momentum space.This dimer counting does not take into account the internal state of the dimer.If the vortex lines between two vortices were braided many times(Fig.13(a)),the vortex dimer couples to the anyon with fractional statistics,which is characterized by the Laughlin wave function.The vortex loop can appear at any local site in the gapless mode of the pairing model but still constructs self-consistent current loops.Thus a fermion pairing lattice with vortex loops is still in a super-conducting state,but the pairing energy gap closes at the vortex arcs.These vortex arcs caused the Fermi arc in the pseudogap state of the unconventional superconductor. The complete Hamiltonian for a positive vortex dimer around the∞shaped loop reads(Fig.15(c)), This Hamiltonian can be further simplified by the string operator,which is a serial product of the particle number operatoralong the track, Each vortex dimer is pinned down by a free fermion pair confined at local site(i,j),on which the energy spectrum is gapped.The unit cell covered by the pure vortex loop is in a gapless state.The global gapless phase only exists for a lattice of isolated vortex loops and vacuum vortex dimers.In mind of the anti-commuting character of fermionic arcs,each fermonic arc can be represented by a composite Grassmann operator, The path integral of gauge potential expdl]=exp[iφ]is only carried out along the fermionic string arcs.The string operator is the product of six Grassmann operators, whereis the product of three fermion arcs around the first vortex of the dimer,andrepresents the second vortex inside the vortex dimer.The ordered Grassmann string operator switches to negative if the order of the six operators is reversed.The string operator of an isolated vortex is equivalent to a Wilson loop operator;it is the product of four Grassmann operators,which is equivalent to a boson.The effective Hamiltonian for a vortex dimer coupled to a fermion pairing state is In the mean- field approximation,the corresponding Hamiltonian in momentum space becomes a dressed fermion pairing Hamiltonian after integration of the Grassmann variable L(k)is the vortex dimer spectrum in the action Eq.(60).The original fermion pairing gap closes at the gapless point of the vortex dimer spectrum,kx=ky,or kx=−ky.This gapless equation induces the Fermi arc in momentum space.The gapless superconducting resonance vortex dimer state along the nodal and anti-nodal line of the energy spectrum offers a theoretical explanation of the pseudogap state of an unconventional superconductor.[35]The energy current of each spin component defines the location of a point of a knot in momentum space.The current knot square lattice is still in the superconducting state in the presence of the vortex.If the two crossing super-currents between two vortices are braided more than three times in the same direction,a Majorana fermion will be generated to raise the local energy,but does not break the pairing states.The fractional statistics of this Majorana fermion can be described by the Laughlin wave function. Fig.16.(a)The two equivalent crossing states with respect to the positive pairing pattern,|+π/4i,|+5π/4i.(b)The two equivalent crossing states with respect to the negative pairing pattern current,|−π/4i,|−5π/4i. When the long-range pairing pattern between two farseparated crossing sites is taken into account,the selfconsistent construction of fermion pairing patterns on the knot square lattice includes four more degenerated patterns(Fig.16),which are denoted as(|+π/4i,|+5π/4i)with respect to|+1i and(|−π/4i,|−5π/4i)with respect to|−1i.The generation of a positive spin with positive momentum is equivalent to the annihilation of a negative spin with negative momentum.This equivalent correspondence obeys the same Feynmann diagram rule for particles and anti-particles in conventional quantum field theory.Within this enlarged crossing state space,one fermion could travel across many unit lattice spaces to meet at the local pairing sites.In that case,the fermion pairing Hamiltonian carries a long-range pairing interaction that shares the same formulation as Eq.(46).The fermion–antifermion pair forms a conserved continuous current without vertical convection current. The multi-knot lattice model can be extended to a honeycomb lattice,triangular lattice,and so on.In order to implement spinors for quantum spins,we have to use double current along each bond as a geometric representation of spinors.The complete Hamiltonian for the multi-knot lattice model of spins includes long-range spin–spin coupling terms, The conventional Ising model,Kitaev model,and other spin–spin coupled quantum models are special cases of the knot lattice model for the nearest-neighbor coupling interactions.The non-commutative character of spin operators induced nontrivial quantum physics beyond classical Ising spin. When the two-state Ising model or block spin-1 Ising model contain more than two different spin component operators,the Ising spin Szcomponent is non-commutative with the other spin components,which induces a more complicated geometric implementation of the eigenstate of quantum spin models.We first take the 1D Ising spin chain model as an example to explore the knot lattice configuration for entangled quantum states.The short-range transverse- field Ising chain model includes both Szand Sx, Replacing Sxiwith Syileads to an equivalent quantum model under duality transformation.The knot representation of this model is two loops periodically entangled with each other(Fig.17).For a vanished transverse field hi=0,the spin chain reduces to the classical Ising model.For the antiferromagnetic coupling Jz>0,the ground state is two loops with the maximal winding numbers;one loop wraps around the other at every lattice site(Fig.17(a)).For ferromagnetic coupling Jz<0,its ground state is two separated loops,i.e.,one loop is above the other everywhere on the whole chain of the lattice(Fig.17(d)).A weak transverse field acts as a perturbation on the ground state by flipping the crossing states from over-crossing to under-crossing(or vice versa)upon a certain number of lattice sites instead of the whole lattice.Meanwhile,if the coupling strength between the nearest neighboring spin drops to zero,Jz=0,the eigenstate of the spin chain is determined by the eigenstate of the spin operator Sxalone,(|↑i±|↓i),i.e.,Sx(|↑i±|↓i)= ±1(|↓i±|↑i).The eigenstate knot lattice of the transverse Ising model is a bilayer knot lattice,the bottom layer carrying|↑i plus(or minus for a positive hi)the upper layer carrying|↓i.If Sxiis replaced by Syiin Hamiltonian Eq.(68),a phase factor eiπ/2must be added to the upper knot lattice layer with|↓i(Fig.3(d))in order to fulfill the eigen-equation of Syi,i.e.,Sy(|↑i± i|↓i)= ±1(|↑i±i|↓i).The transverse Ising model admits a quantum phase transition when the neighboring coupling strength equals the transverse field strength Jz=h.This critical point is derived by the exact solution of this Ising chain model,which maps spin coupling onto the fermion pairing Hamiltonian[36]by Jordan–Wigner transformation Eq.(10), This pairing Hamiltonian can decompose into a coupling type between pseudo-spin and complex fermions similar to Eq.(48), where εk=2[h−Jzcos(k)],∆ =iJzsin(k).ψk=[ck,c†k].The critical point of this conventional transverse Ising model lies at the gapless point,where the exact spectrum vanishes, For the ferromagnetic coupling at the critical point,Jz=h<0.The Ising coupling drives the ground state of each layer into a state with two separated loops(Fig.17(d)).The transverse field prefers a superposition state of two layers of knot chains with opposite global crossing states and a plus sign between them.Thus the ground state of this quantum Ising model is composed of four separated loops.In order to reach the gapless state,an odd number of spins must be flipped on the two layers simultaneously.This inevitably increases the winding number of the four loops.Another operation is to add a exp[iπ]phase factor to certain lattice sites in one layer,but keep the other layers the same.This operation increases the energy by units of the transverse field.Adding a exp[iπ]phase to a spin state is equivalent to flipping its state to the opposite,i.e.,from(|↑i+exp[iπ]|↓i)=(|↑i−|↓i)to(|↑i+|↑i).The decreased energy in the output of Sxis transferred to the increased part in the output energy of Sz.The neighboring coupling and transverse field compete with each other to reach a balance point of energy output,which is the critical point of the quantum phase transition.The energy carrier here is actually kink excitation.The total winding number is the total number of kinks in the loop chain.The maximal number of kinks on a chain of 2N spin is N.The maximum winding number is also N.The total winding number at the critical point is zero.The total winding number above the critical point has the opposite sign to that be low the critical point.The total winding number here is the linking number of the four entangled knots.In this sense,this quantum phase transition is also a topological phase transition.Since the effective spin component has only one wave vector,it cannot draw a 2D loop in momentum space.However,if auxiliary parameters and the next-nearestneighbor interaction are introduced in an extended transverse Ising model,the closed loops in the auxiliary parameter can still characterize the quantum phase transition.[37] The spin flipping in this 1D chain can be implemented by the same braiding operations for Ising spin in a 2D lattice(Fig.3(a)).One spin flipping is realized by at least two braidings in the same direction.Single braiding could result in a vacuum state that is not the eigenstate of the two-state Ising spin.Thus we extend the two-state Ising spin to block spin-1 operator,Siαhas three eigenstates,|±1i and|0i.For a spin chain oriented along the X direction,there are two independent braidings.One iswhich generates one up and one down Majorana fermion arcs(the green arcs in Fig.17).The other is,generating a left and a right Majorana fermion arc.These braiding operators are implementable by magnetic field.If the spin chain is acted upon only by,the resulting vacuum state is composed of N unit circles for N lattice sites.This is the dimerized insulator state(Fig.17(b)).For the other global braiding operation of,the generated vacuum state is two separated loops(Fig.17(c)).Particles can run through the whole lattice but split into two bands.If there are only twobraidings on the left and the right edge correspondingly,andbraiding over the whole inner section,the two separated loops can fuse into one.This leads to the gapless vacuum state.Different vacuum states can be distinguished by the topological numbers. Similar to the 2D block spin-1 Ising model,this block spin-1 Ising chain also has non-Abelian anyons in the eigenenergy level.The superposition of the vacuum state and Majorana fermion state is naturally embedded in the Hilbert space.The eigenstate in the vacuum state is a natural quantum qubit for topological quantum computation.[1]Repeating the braiding operations drives the Majorana fermion to jump from the bottom layer to the upper layer(or vice versa).The topological correlation for this block spin-1 chain is easier to calculate than the 2D lattice model.The Jones polynomial for a given quantum state here is exactly computable by the Skein recursion relation,which views the vacuum state as the superposition of|↑i and|↓i.Thus every quantum state is associated with a Jones polynomial.However,different states may share the same Jones polynomial;we call it topological degeneracy,which fulfills the requirement for topological quantum computation. Fig.17.The two entangled loops as eigenstate representation of 1D transverse Ising model. Since there are three currents intersecting at one lattice site,we abandon the magnetic monopoles and positrons to avoid local frustrations.Here we introduce three colors of anyons,red(σR),yellow(σY),and blue anyons(σB).A pair of anyons is running in two currents oriented by one arm of the local tribein which has three arms separated by 2π/3.One possible implementation of σRis an electron attached by a flux phase factor expA,so does σYand σB.An overcrossing occurs on each arm of the tribein which is enveloped by an hexagonal unit cell(Fig.18).Three sequential braidings at the three intersecting squares obey the Yang–Baxter equation(Figs.19(a)and 19(b)), Here Rσpσqare the braiding operators on the over-crossing points.Thus a rotated tribein or its mirror configuration is equivalent to the original coupling tribein.We first input Ising coupling between neighboring unit cells, The local crossing state of each arm in the i-th unit cell is only acted on by Siz.The conventional Ising spin on the lattice is represented by a single↑ior↓i.Here,every unit cell has three internal spin components that have the freedom to point up or down.In order to implement the classical Ising model,we only choose two block spin configurations,|⇑ii=|↑↑↑iiand|⇓ii=|↓↓↓ii.The knot configuration in Fig.19(a)corresponds to|↑↑↑ii.Flipping all of the three crossing states of Fig.19(a)results in|↓↓↓ii,which indicates the generation of the statistical phase exp[iπ].Each spin flip is performed by braiding one pair of anyons twice.Three spin flips requires six times of braiding anyons on the three arms.Thus each anyon carries a statistical phase factor,exp[iπ/6]. Fig.18.One layer of the multi-layer knot patterns for effective mapping of Ising model and Kitaev model on honeycomb lattice. Fig.19.(a)Three-color anyon currents entangled with each other to implement the local tribein for the Ising model on a honeycomb lattice.The three braidings satisfy the Yang–Baxter equation.(b)Three-color anyon currents entangled with each other to implement coupling style in the Kitaev honeycomb model.(c)The fusion rule of the three-color anyons into two-color Majorana fermions in the Hilbert section of Sz,and the fusion of two Majorana fermions.(d)The fusion rule of the three-color anyons into three-color Majorana fermions in the Hilbert section of Sz. The coupling interaction between crossing points within the hexagon unit cell can also be introduced to construct an Ising model on a Kagome lattice.[38]The three frustrated spins within the triangle lattice either generate three kinks or one kink.The block up-spin/down-spin above represents three kinks running in the clockwise/counterclockwise direction.The single kink state exists for the case that one current is above the other two,which always have one current lifted in the opposite direction.These frustrated states are generated by spin flipping upon|⇓iior|⇑ii, They are in fact frustrated triple spin states on a triangle lattice,obeying the following Hamiltonian, The coupling term within the unit cell has an equivalent formulation by the sum of three arm spins, The ground state requiressince the sum of the three arm spins cannot reach zero.The frustrated spin configurations Eq.(73)are the ground state.The first excited state of the single hexagonal unit cell is E=3Jz,which corresponds to the three kink states.E=−Jzcorresponds to the six degenerated single kink states(Eq.(73)).Only flipping one spin could transform the ground state with a single kink to the first excited state with three kinks.One spin flip contributes a exp[iπ]phase factor to the block spin.Here,a spin flipping is performed by braiding two anyons twice.Thus each anyon carries an Abelian phase factor exp[iπ/2].Each braiding costs an energy unit 2Jz. For a single triangular unit cell,braiding anyons within the ground state shows other statistical phases.For instance,in order to map|↑↓↑iito|↓↓↑ii,only the spin in exis flipped by braiding anyons twice.The collective wave function acquires a phase exp[i2π].Thus the anyon in excarries a phase exp[iπ].Meanwhile,mapping state|↑↓↑iito|↓↑↓iirequires three spin flips,which is carried out by six braidings on local tribein.Thus each anyon carries a statistical phase exp[iπ/3].The statistical factors of anyons are not uniformly distributed along different mapping paths from one eigenstate to another.Thus we call the anyons within these frustrated states non-Abelian anyons. These highly degenerated frustrated states have an exact one-to-one mapping to multi-layer knot lattice configurations similar to what we showed before.Thus each state could be labeled by a topological linking number of those entangled loops.This topological linking number is in fact equivalent to the total magnetization of spins.One special topological character of these frustrated states is that there exists at least one current that can be disentangled from the other two without cutting at each local triangle.Repeating this operation for all of the other five triangles around the hexagon plaquette,we can always find a free loop current around the local hexagon plaquette.Anyons keeps running in this loop around the hexagon plaquette without losing energy or charges,but generate a magnetic flux passing through the center of the hexagon plaquette.As shown in the last section,electrons running in the knot lattice model bear the quantum Hall effect.For this two-state Ising spin on a Kagome lattice,it only implements the quantum Hall effect with an even number of magnetic fluxes.The two-state Ising spin Szi=±1 on this Kagome lattice must be replaced by three-state Ising spin Szi=±1,0 in order to implement the fractional quantum Hall effect. This knot lattice model can also be constructed to explore non-Abelian anyons in the gapless phase of the Kitaev honeycomb model.[10]The knot patterns for constructing a honeycomb lattice are shown in Fig.18;here the local tribein is acted on by different spin operators on each arm, Different ferromagnetic coupling strengths are assigned in each direction of the local tribein,i.e.,Jl<0,(l=x,y,z).Here(Sx,Sx,Sx)are spin-1/2 operators.In the knot lattice model(Fig.18),we introduce three colors of anyons,red(σR),yellow(σY),and blue anyons(σB),to implement this anisotropic coupling type.The knot pattern generated by the red and blue anyons is only acted on by spin operator Sx.Syacts on the red and yellow anyons,while Szacts on the yellow and blue anyons(Fig.19(a)).The Yang–Baxter equation still holds for this knot lattice(Fig.19(a)).Extending this anisotropic coupling tribein over the whole honeycomb lattice,it naturally leads to an equivalent model to the Kitaev model on a honeycomb lattice,except here every local coupling tribein has been rotated for consistency(Fig.18). The three color anyons carry topological color charges.A running red anyon generates a yellow and blue field to drive the motion of the yellow anyon and blue anyon,respectively.In the gapped phase of this knot lattice model,these anyons obey Abelian anyon fusion rules(Figs.19(b)and 19(c)), When the three tribein all fuse into Majorana fermions,a triplet of Majorana fermions is left in the middle,ψRψYψB,which is a fermionic cluster(Fig.19(c)).The knot lattice model has three conserved plaquette operators around three adjacent hexagon plaquettes(Fig.18), Here,(1,2,3,4,5,6)indicates the six lattice sites around each hexagon.WRdraws a closed loop around the red loops in Fig.18,as do the blue loops and yellow loops for WBand WYon other hexagon plaquettes.The plaquette operator is in fact a Wilson loop,which can be viewed as a generalized magnetic flux.A conserved color anyon runs in each Wilson loop.These Wilson loop operators commute with the Kitaev Hamiltonian,[Wp,Hk]=0,(p=R,B,Y).Thus the Wilson loop and the knot lattice share the same ground state.The minimum energy state of the knot lattice model is reached at a vortex-free state,i.e.,Wp=+1.A vortex is generated in the plaquette if Wp=−1. The knot lattice pattern of the ground state in each plaquette consists of(26−1)layers of link lattice,since each Wilson loop operator is constructed by six effective spin operators.The eigenstate of the Wilson loop operator is a superposition state of six spin values,which is either|↓i or|↑i.The ground state of this Wilson loop is a spin-liquid state,which does not show a magnetically ordered state.We denote the spin configuration at the ground state of the Wilson loop operator as, For example,the eigenstate of the Wilson loop operator,WR,is the superposition state of every possible spin configuration with an even number of|↓i, Flipping one spin at any one of the six sites generates a plaquette vortex.For the other two plaquette operators,WBand WY,the spin configuration of the ground state consists of a bilayer knot lattice,so that the spin operator fulfills the eigen-equation at every lattice site, One exemplar bilayer knot pattern that fulfills the equations above is the sum of two layers(Fig.20).The eiπ/2phase factor on the Syisector is assigned by its eigenstate construction Eq.(81),while the eiπ/2phase factor on the Szisector is assigned by the commutator relation of spin operators,SaSb=iεabcSc.For the negative eigenvalue of Sip,Sip|↓ii= −1|↓ii,we introduce a minus between the two layers.The Sxand Sysector state spontaneously flipped a sign.To avoid the vanishing of the eigenstate of Szi,we add an eiπphase upon the the sector of Sziin the second layer.At the same time,to satisfy the equation SaSb|gi=iεabcSc|gi,the product of the eigenvalues of Sxand Symust be negative to be consistent with the eigenvalue of Szi.Thus we add an eiπphase shift to the sector of Sy.Repeating this knot lattice construction process for the six spins of the plaquette,we can derive the superposition state of 62 layers of the knot plaquette as the eigenstate of the Wilson loop operator. Fig.20.(a)The knot configuration of positive eigen-energy state of spin operator.(b)The knot configuration of negative eigen-energy state of spin operator. Braiding the color anyons in the knot lattice with respect to the eigenstate of the Kitaev model follows the same fusion Eq.(12)as that for the Ising model.Unlike the bilayer configuration of the Ising ground state,the ground state of one plaquette in the Kitaev honeycomb model has 62 layers.Braiding two anyons across the 62 layers synchronously in a clockwise(or counterclockwise)direction would generate either a vacuum state or a Majorana fermion state in each layer following the basic fusion rules, The anyon braiding in the Sxand Sysectors carries phase factors due to the commutator relations of spin operators and the eigenstate construction. The knot lattice in real space also maps out the knot configuration in momentum space,since the energy of the system is independent of representation parameters.The fermion operator on the knot lattice has periodical distribution in real space,thus it has a natural mapping into momentum space by Fourier transformation.Then the huge number of knot lattice layers in which electronic waves propagate could reduce to a statistical distribution of oscillating frequency in the wave vector space.This distribution is summarized by the spectrum of the interacting system.The spin-1/2 Kitaev Hamiltonian was mapped into a quadratic fermion Hamiltonian,which is equivalent to a complex fermion pairing Hamiltonian.[10,39,40]In Kitaev’s Majorana fermion pairing representation of one spin operator,[Sα=ibαc,(α =x,y,z)],the spin–spin coupling Hamiltonian is mapped into a fermion coupling Hamiltonian in momentum space,[10] here α,β represent the local tribein[ex,ey,ez]inside each unit cell.The spectrum matrix has an off-diagonal representation, where the spectrum function f(k)=2(Jxeik·r1+Jyeik·r2+Jz).riare the translational invariant unit vectors on the hexagonal lattice,which point to the next nearest neighbor unit cell,.The energy spectrumThe Kitaev Hamiltonian in momentum space can also decompose into a fermion–spin coupling formulation, where Sxand Syare conventional Pauli matrices.The currents along the direction of the x-spin and y-spin components are These two currents depict the Fourier knot in momentum space,which usually express the variable kxby spatial frequency and a free parameter,i.e.,(kx=ωxk,ky=ωyk).These two currents are actually the projection of the energy spectrum to X spin and Y spinIn the exact solutions by Jordan–Wigner transformation,Iy= εkrepresents the kinetic energy of the free fermion.Ix=∆is the energy gap for exciting a fermion pair.The energy spectrumhas a similar form to the p-wave BCS pairing model.If we consider the evolution of a time-dependent knot lattice state with eigen-energy E(k),its final state oscillates as a matter wave,|ψfi=Aexp[(i/ħ)Et]|ψii.A higher E(k)indicates a faster oscillation with higher energy.In the mean time,the energy current also oscillates in space.ωxcounts the number of oscillations in unit space along the X direction.The Kitaev model in momentum space is an effective coupling model between a fermion and pseudospin vector.When the pseudospin vector rotates in momentum space,the fermion current in the color channels also fluctuates following the time-dependent Heisenberg equation.In the gapless phase E=0,the Majorana fermion in each unit hexagon cell has a constant existence probability even though it still oscillates from site to site.The flipping probability of the current crossing state of the multi-layer knot lattice has a static value.The gapless spectrum exists when the three coupling coefficients satisfy the following inequalities,[10] In this case,the three coupling bonds of the local tribein reach a balance,then the non-commutative characteristic of the three component spin operators dominates the system.The gapless phase is an ordered phase of spin liquid which shows up after the quantum entropy generated by oscillating Majorana fermions is suppressed.The gapless phase in the Kitaev model corresponds to a vanishing spectrum of the fermion pairing system,which is in fact the locations of vortices in momentum space. The Fourier knots of current and the corresponding normalized current in momentum space have different topologies for different phases(Fig.21,Fig.22).In the gapless phase(with parameter setting(Jx=40,Jy=10,Jx=40)),the serial knots for different frequency ratios draw different knots around a forbidden hole in the middle.For the equal frequency,1:1,the knot is a simple circle(Fig.21(a)1:1).It draws a trefoil knot for 1:3 and an overlapping trefoil knot for 6:1.For other ratios,ωx:ωy=1:ωy,the knot wraps ωyrounds with a winding number W= ωy(Fig.21(a)).For other ratios,ωx:ωy= ωx:1,the winding number is W=ωx.For arbitrary frequency ratios,the winding number is W=ωx+ωy−1.As the frequency goes higher to ωx:ωy=1:100,the knot in momentum space approaches to a toroid plate(Fig.22(e)).The corresponding normalized currents(nx=Ix/E(k),ny=Iy/E(k))depict an open band(Fig.22(f)).In the meantime,the two oscillating bands touch each other periodically along k=0(Fig.22(d)).For the gapped phase,the energy current draws serial knots which pass the interior of a circular area without a forbidden hole(Fig.21(b)).It winds ωyclosed loops for frequency ratio ωx:ωy=1:ωy.The trefoil knot also appears for the frequency ratio ωx:ωy=3:1(Fig.21(b)).The energy spectrum shows two separated bands with many oscillations enveloped in one wave package(Fig.22(a)).The energy current knot turns into a filled disc at the high frequency ratio of ωx:ωy=1:100(Fig.22(c)).The corresponding normalized current also depicts a complicated knot which winds into a closed half-moon shape(Fig.22(c)).Thus the energy current of the gapless phase has a Euler characteristic χ=0,while the gapped phase has a nonzero Euler characteristic,χ=2.This knot lattice implementation of the Kitaev model has a straightforward extension into a knot lattice in 3D by the anyonic loop model.[41] Fig.21.(a)The Fourier knot serial in momentum space for the gapless phase of the Kitaev model with respect to different frequency ratios,ωx:ωy.The parameter setting is[Jx=40,Jy=10,Jx=40].(b)The Fourier knot serial with respect to different frequency ratios in the gapped phase of the Kitaev model.The parameter setting is[Jx=10,Jy=10,Jx=40]. The block spin-1 Kitaev honeycomb may also demonstrate the fractional quantum hall effect.Most crossing lines become turning arcs that transform one type of anyon into another.The conserved plaquette operators still exist for this block spin-1 Kitaev Hamiltonian due to the same commutator relation of spin operators.The three plaquette operators,[Wp,(p=R,B,Y)],bear the same formulation as Eq.(78).The ground state of this block spin-1 plaquette operator is the same as that of the spin-1/2 Kitaev Hamiltonian.However,the plaquette excitations are completely different from that of the spin-1/2 Kitaev model.The first excited state is determined by Wp=0,(p=R,B,Y).If any one of the six unit cells of the hexagon plaquette joins in the vacuum state of the zerocrossing state,then it generates one plaquette excitation that we call vacuum excitation.There exist 62 possible vacuum excitations in total.The topological operation of these vacuum excitations is to disentangle two neighboring loops.The vacuum excitation is generated by braiding two anyons once(Fig.18(d)).Braiding anyons twice upon the ground along the same direction leads the plaquette to the second excited state.The three states of S=±,0 are eigenstates of the Szsector,while in the Sxor Sxsector,an even number of braidings plus Majorana fermion flipping does not generate the eigenstate of Sx.In that case,the bilayer knot of eigenstates for Sxor Syhave to be acted on synchronously. Fig.22.(a)The energy spectrum of the gapped phase,with[Jx=10,Jy=10,Jx=40],and frequency ratio,ωx:ωy=1:100.(b)The Fourier knot of current in momentum space in gapped phase. (c) The knot of normalized current in momentum space of gapped phase with the same parameters as panels(a)and(b).(d)The energy spectrum of the gapless phase,with[Jx=40,Jy=10,Jx=40],and frequency ratio,ωx:ωy=1:100.(e)The Fourier knot of current in momentum space of gapless phase.(f)The knot of normalized current in gapless phase with the same parameters as panels(d)and(e). For a finite lattice without periodic boundary condition,the boundary coupling types have to be carefully arranged in order to map the Kitaev model consistently.Because there are always three color string branches on the upper boundary or bottom boundary,there is no way to connect the strings with the same color without over-crossing or under-crossing another current.The only consistent connection pattern is fusing color anyons into colored Majorana fermions(Fig.23).Two edge currents of mixed anyons and Majorana fermions exist both on the upper boundary and bottom boundary(Fig.23).However,if the lattice structure is not a perfect hexagonal lattice,instead containing certain plaquettes formed by the odd number of edges,then the anyons in the edge current do not obey Abelian fusion rules.There must exist some fermionic vacuum state and unpaired Majorana fermions.For instance,the minimal extension of the spin-1/2 Kitaev model on a lattice with odd plaquettes is the tetrahedron lattice,which is constructed by four triangles.[42]The Hamiltonian simply reads(Fig.24(a)), The tribein of each lattice cannot directly connect to its neighboring sites without introducing extra crossings(Fig.24(a)).If extra over-crossings are introduced for consistency,the tetrahedron lattice model finally turns into a honeycomb lattice model again.If a vacuum and an exotic Majorana state are introduced on the edge bonds,the Kitaev-type tetrahedron model can also be constructed consistently(Fig.24(b)).However,the anyon on the edges obeys exotic fusion rules Thus Abelian anyons run in the inner land current channels and obey the conventional fusion rule Eq.(77).Non-Abelian anyons run on the edge and generate Majorana fermions and a fermionic vacuum(grey bonds in Fig.24(b))simultaneously.There are three unpaired Majorana fermions running in the edge loop.Odd loops break the time-reversal symmetry under the transformationThus the three running Majorana fermions run in one direction,either in the clockwise direction or in the counterclockwise direction. Fig.23.The consistent existence of edge current on the upper and bottom boundary of Kitaev model on honeycomb lattice. Each spin operator in the Kitaev honeycomb model is expressed by a pair of Majorana fermions,[10]Sαj=ibαjcj.In the vacuum state of this knot lattice model,bxjrepresents a yellow arc,byja blue arc,and bzja red arc.cjcorresponds to the fermionic arc forming the closed loop around the j-th lattice site.The effective Majorana fermion Hamiltonian of the gapless current reads(Fig.24(b)), whereˆojis a fermionic vacuum operator,which has an effective representation by Clifford algebra.The product of the three bond operators,uij=cyicyj,constructs a Wilson loop operator,W=WaWbWcu24u23u34,with(Wa,Wb,Wc)as the other part of the three independent loops.This Wilson loop operator commutes with the bulk Hamiltonian.The edge Hamiltonian reduces to a single fermion operator under a fixed gauge,uij=+1, Thus the coupling type between spins on the edge is translated one step back along the coupling parameter sequence.The fermionic vacuum exists as a quasi-excitation coupled to an unpaired Majorana fermion. Fig.24.(a)The knot lattice of four spin’s tribein mismatch each other on each bond. (b) The knot configuration of edge states with exotic fusion rules.The grey arcs indicate fermionic vacuum strings. To generate chiral anyon current on the boundary of the honeycomb lattice,we can introduce a pentagon or triangular plaquette on the upper boundary or bottom boundary.For an extension of the Kitaev model on a lattice with odd plaquettes,[43,44]this chiral edge current was born to exist on the boundaries.The most general Hamiltonian for the edge current of the non-Abelian anyon chain model reads, Here b is a general Majorana fermion.ˆo is a fermionic vacuum operator.One usual construction of Majorana fermions by a conventional fermion operator is The ground state of this Majorana fermion is|gi=(|0i−while the vacuum fermion has no conventional construction.The only self-consistent construction of a vacuum fermion and Majorana fermion simultaneously is based on the knot lattice chain model(Fig.17).The creation operator can be defined as the product of two clockwise braiding operators(Fig.25),while the annihilation operator is the product of two counterclockwise braiding operators.The vacuum operator is also a product of braiding operators(Fig.25(a)), The creation operator,annihilation operator,and vacuum operator have two different representations by braiding operators in different directions(Fig.25(a)).In order to match the conventional symbol of quantum operators,we replace the symbols(?and?)with(−and+), The indices n and t indicate the normal and tangential direction along which the braiding is performed.The fermion chain model of non-Abelian anyons is expressed by pure braiding operators, where the fermionic vacuum operator is The non-commutable characteristic of braiding operators is consistent with non-Abelian anyon statistics.The eigenstate of this non-Abelian anyon Hamiltonian can be constructed by the sum of two knot chains(Fig.25(b)),i.e.,Htc|ψi= ±|ψi.For an isolated crossing state,the single braiding operator is neither fermion nor boson.Since exchanging two pairs of double braiding operators contributes exp[iπ],each braiding is equivalent to an anyon which bears an effective statistical factor exp[iπ/2].However,if there exist many connected neighboring zero-energy states and only a few crossing states,the statistical phase factor from collective spin-up to spin-down is not exp[iπ]anymore.In that case,the statistical phase is determined by the filling factor, where N(B)is the total number of braidings to transform one collective state into another one.This number has a straightforward counting from a Hamiltonian in real space.An equivalent counting can also be performed in momentum space under Fourier transformation, The anyon fermion pair model is mapped into a coupling model of four braiding operators.The braiding operator in momentum space braids different energy levels.The spin currents with opposite spin in the quantum spin Hall effect cannot cross each other in the energy spectrum;this defines an over-crossing state or under-crossing state.The level crossing avoidance point defines the different vacuum state.Higher excited knot states of energy levels in momentum space also exist for non-Abelian anyon models. Fig.25.(a)Two sequential braidings map one spin state to another state,and one vacuum state to another.(b)The eigenstate of knot lattice for the gapless edge current Hamiltonian. The gapless edge current is actually a 1D Majorana fermion chain including vacuum state.A 1D quantum chain of ordinary fermions with long-range hopping terms is a more general case of non-Abelian anyon. Here m is the distance number that counts the number of lattice sites between two lattice sites that are connected by continuous long-range channels.In the presence of the long-range hopping Hamiltonian Eq.(100),long loops covering many sites would show up in the eigenstates.For the exemplar strip ordering phase in Fig.26,the long-range hopping Hamiltonian reads, Suppose there exists a string of gapless modes covering four neighboring unit cells(Fig.26(a)).Under one braiding operation at the first sites(Fig.26(a)),it generates one|+1i state.This knot maps to a trivial circle by Reidemeister moves.The output state under two braidings is|+1,−1i(Fig.26(b));this knot has a linking number Llink=1,which results in a filling factor ν=1/2.The output knot under three same braidings is|+1,+1,+1i.It takes one flip on the second or two flips on the first and third sites to map onto a trivial knot state,thus the filling factor here is 1/3 or 2/3.The strip knot has eight alternative crossings(Fig.26(d))after eight braidings,and has a linking number of Llink=4.In order to map the maximal linked state onto a trivial circle,it takes four flipping operations at the second,fourth,sixth,and eighth crossing sites.Then the ferromagnetic phase of this strip loop could be mapped onto a trivial circle by Reidemeister moves.This defines a collective vacuum state(Fig.26(e)).Each flipping operation is equivalent to a Majorana fermion operator.The four flips require eight braiding operators.Thus the filling factor of this collective vacuum state is ν=4/8=1/2.This is a local filling factor.It turns into a global filling factor for a periodical distribution of strip knots over a 2D knot lattice(Fig.29).If the strip vacuum state covers 2n unit cells,the filling factor could reach(n±1)/2n.In this sense,the fractional filling state is essentially a topological finite-size effect. Fig.26.(a)One vacuum strip knot covering four neighboring unit cells.(b)and(c)The strip knot under one and two braidings.(d)The strip knot after eight braidings.(e)The disentangled strip knot after four flipping operations by Majorana fermion ψ. The Haldane model on a honeycomb lattice demonstrates a quantum Hall effect without Landau levels.[45]The honeycomb knot lattice can also construct the eigenstate of the Haldane model(Fig.17,Fig.27).The honeycomb lattice is composed of two triangular sub-lattices.In the Haldane model,besides the hopping of fermions between nearest neighbors,the hopping of fermions among the next-nearest-neighbor sites is also introduced,[45]The phase factor is φ =2π(2φa+φb)/φ0.If the next-nearestneighbor sites are directly connected by continuous current channels(for instance,the knot lattice in Fig.27),the nextnearest-neighbor hopping terms in Hamiltonian Eq.(102)can be directly performed on the knot lattice to flip the local crossing state.However,every lattice site must be an over-crossing state or under-crossing state in order to keep a continuous channel connecting any next-nearestneighbors.If there exist some block spin|0i states on certain lattice sites,there would not exist a minimal channel to connect certain nextnearest neighbors(Fig.19(c)).Thus a superposition state of many honeycomb knot lattices with only crossing states can construct the eigenstate of the Haldane model.Since the braiding operator is only allowed to perform on two states,|+1i or|−1i,the dominator of the filling factor can only be an even number.The opposite writhing current(Fig.7)can implement the two opposite magnetic fields on the renormalized sublattice.The Hall resistance in the integral quantum Hall effect is quantized by the first Chern number of the Berry phase.The first Chern number is equivalent to the Euler characteristic on a discrete lattice.In order to map the Chern number to the Euler characteristic,the energy current in momentum space must be triangulated into a grid.How to derive an exact mathematical mapping is still an unsolved problem in mathematics. Fig.27.One of many layers of honeycomb knot lattice implementation of the Haldane model with the next-nearest-neighbor hopping terms for integral quantum Hall effect. As shown in the last section,the fractional filling factor in the quantum Hall effect is essentially quantized by the linking number of crossing current.The block vacuum state in the block spin-1 knot lattice is inevitable to produce fractional quantum Hall states.As we have already seen in the knot square lattice model,more braiding within one unit square inevitably creates more lattice sites within the unit square.This means the fractional Hall effect only exists for long-range hopping dynamics to derive a higher linking number.Since the fractional filling factor only depends on topological braiding operations,it is independent of a specific lattice structure.Each lattice site must admit a block spin-1 state, i.e., two crossing states(|+1i,|−1i)and two vacuum states(|0ti,|0ni).A global vacuum state is a set of minimal loops around the center of each unit cell;there is no next-nearest-neighbor hopping.The global vacuum state does not match the Haldane model with next-nearest-neighbor hopping terms.If all of the vacuum states are placed on B lattice sites and none on A lattice sites,the next-nearest-neighbor hopping still survives to construct the Haldane model(Fig.27).It takes three braidings to bring the trefoil knot around A into vacuum states,and the corresponding writhing number decreases from three to zero.Three crossings were eliminated during this braiding process.Thus the filling factor of the vacuum excitation is one. Fig.28.(a)and(b)The energy spectrum and knot of the Haldane model in momentum space with respect to different phases φ and on-site energy M=1.(c)The knot of the Haldane model in momentum space on-site energy M=0.The frequency ratio for the figures above is ωx:ωy=1:100 and t2=−2. The energy spectrum of the Haldane model in momentum space[45]can be decomposed as a function of the Fourier knot drawn by the three energy currents with respect to the three spin components, The Hall conductivity σxyis quantized at the Fermi level,ν(e2/h). The integer here ν =+1(ν = −1)for φ >0(φ<0).[45]This integer measures the sign of the winding number of knots in momentum space.The circular trefoil knot in momentum space for φ =−3.14 and φ =−1 turns into the opposite direction of that for positive phases,i.e.,φ=3.14 and φ=1(Figs.28(b and 28(c)).The phase φ only modifies the initial phase of the oscillating energy spectrum wave,but does not change the gap characteristic between two bands,except here the energy gap reaches the maximal value at zero phase(Fig.28(a)).The trefoil knot in momentum space here is the dual mapping of the trefoil knot in real space(Fig.27). Fig.29.The square knot lattice of double currents for implementation of Haldane model and Kane–Mele model. The Haldane model is a topological band model with Chern number C=1.A topological flat band model with Chern number C=2 could be constructed on a square lattice with third-nearest-neighbor hopping.[46]This square knot lattice is a natural implementation of the Kane–Mele model,[47]which induces spin–orbital coupling in the Haldane model.[45]Each unit cell here is composed of four unit squares with internal crossing currents.Fermions with opposite spin run in separate channels(the purple channel and black channel in Fig.29).For those channels turning left(right)to reach the next nearest neighbors,µij=+1(µij= −1).The eigenstate of the Kane–Mele model can be constructed by multi-layer knot configurations without block vacuum state.In order to implement a higher order of fractional quantum Hall states,the Kane–Mele model must be extended to include long-range hopping terms.A multi-layer generalization of the Haldane model with third-nearest-neighbor hopping is the topological flat band model with arbitrary Chern numbers.[46]The same physics hold for the Haldane model on a honeycomb lattice with third-nearest-neighbor hopping, Three layers of knot lattice construction of the Haldane model on a honeycomb lattice generates a topological band model with Chern number C=3,[46]as well as Chern number C=2.[48]Note that inter-layer hopping does not exist in this construction.A straightforward construction of the topological flat band model with Chern number C=N consists of an N-layer Haldane model with third-nearest-neighbor hopping.[46] Fig.30.Examples of elementary knot patters for different long-range hopping terms for a topological band model of fractional quantum Hall states. One exemplar knot lattice for the fractional quantum Hall state of 1/3 filling is a topological flat band model with Chern number C=2.The local knot pattern on the 2D square lattice visualizes the hopping distance of particles.For instance,the next-nearest-neighbor hopping on a square lattice runs through a small knot(Fig.30).The next-next-nearestneighbor hopping runs along the big cross channel. The fourth-neighbor hopping terms run along two entangled loops covering many unit cells either along the horizontal line or vertical line(Fig.30).The vacuum state within one unit cell acts as a cut-off of a long knot pattern.To construct a knot lattice with respect to the fractional quantum Hall state,a combination of these basic knot elements is arranged periodically on the whole lattice.Similar to the 1D strip knot,the initial state of the big crossing-knot could be set to the vacuum state or ferromagnetic state.The filling factor for a given knot state is determined by its linking number and the number of braidings to reach that state from the initial state.The fractional quantum Hall effect exists naturally in this knot square lattice since electrons that run in the channel always turn from the X direction to the Y direction or vice versa.The long-range hopping terms in the Hamiltonian also expand the energy spectrum of free particles into extra parameter space.Each energy level in the conventional model containing only nearest-neighbor hopping terms now expands to many hyper fine levels.The conventional fully filled energy levels now become partially filled,which results in fractional filling states.Fractional filling states bear a topological origin;they do not depend on the specific lattice structure.A triangular knot lattice can also be constructed for the topological flat band model with Chern number C=3(as shown in Fig.31). Fig.31.The knot triangular lattice for implementing topological flat band model with Chern numberC=3. The minimal vacuum loop excitation in the square knot lattice model is different from that of the honeycomb knot lattice.There are four Majorana arcs surrounding one lattice site to form the minimal loop in the vacuum excitation of the square knot lattice(Fig.29).Thus each vacuum loop excitation behaves as a boson.Meanwhile the minimal vacuum loop around the center of each hexagon unit cell is formed by three Majorana fermion arcs,thus the vacuum loop behaves as a fermion(Fig.19(d)).Every pair of Majorana fermion arcs indicates the existence of one magnetic flux.Similar to the block spin-1 Ising model,if the crossing state is braided many times,it would generate extra crossing points within one unit cell.Then the Majorana fermion operator as a crossing state flipper has to be introduced to bring the crossing back to the Hilbert space. A more direct implementation of the fractional quantum Hall effect on a honeycomb knot lattice is to introduce an external magnetic field by placing one Dirac magnetic monopole at the center of a sphere lattice,or one magnetic monopole ring around the center line of a torus lattice.Then the input electrons carrying different gauge phases flow into different knot channels.Its Hall resistance bears the fundamental character of the fractional quantum Hall effect.The partition function of the knot lattice is still a topological invariant.However,every hexagon unit cell is attached by a complex coefficient.The total linking number of the knot lattice is now a complex number as well.We could start with the vacuum state without crossing at any lattice site and use the Skein relation and Jones polynomial repeatedly to compute the partition function. The entangled multi-knot lattice model is essentially a new geometric representation of a quantum many-body system with long-range coupling interaction.It naturally encodes Abelian anyons,non-Abelian anyons,integral and fractional quantum Hall states,and so on.Under exact one-to-one mapping between the over-crossing or under-crossing states of two current lines and the eigenstate of quantum operators,an arbitrary eigenstate of the quantum many-body model can be exactly represented by knot lattice patterns.Then each quantum state bears a topological character due to the topological field theory of many knots.In the case of short-range coupling interactions,this multi-knot lattice model spontaneously reduces to a conventional quantum spin model.The eigenstate is a collective wave function of many entangled loop currents.The integral and fractional filling factors for the collective eigenstate of this knot lattice model originate from the topological linking number of many knots,which can be computed by Chern–Simons field theory.The fractional statistics of anyons are explicitly demonstrated by the braiding operation on crossing states.The anyon physics revealed by this knot lattice model have widespread existence in conventional fermion and spin models,such as the Ising model,quantum Hall system,topological insulator model,[49,50]BCS fermion pairing model,Kitaev model,Haldane model,and Kane–Mele model.It offers knot representation on Ising anyons,an exact computation of integral and fractional Hall conductance by linking number com,Lissajous knot representation in the momentum space of the topological insulator,and a new explanation to the pseudo gap state by vortex dimer state.This knot model also predicts two edge currents moving in the same direction on an odd width of lattice,and fractional filling states in the vortex dimer state as well as the multi-vortex state in unconventional superconductors.Different quantum phases can be quantified by different topological linking numbers.For instance,the linking number shows different values in the disordered phase of the Ising model from those of the magnetically ordered phase.The linking number is computable by the Jones polynomial and non-Abelian Chern–Simons field theory,[16]as well as the Abelian Chern–Simons action,[17]which includes the self-linking number,writhing number,and twisting numbers. The multi-knot lattice model has spontaneous extension to 3D lattice models, such as the Ising model, extended Kitaevtype model,[41]and so on.Since the Chern–Simons action is also a topological action of 3D knots,[51]a periodical lattice of 3D knots can be extended to study the 4D quantum Hall effect.[52]The multi-knot lattice also has many theo-retical extensions in Chern–Simons field theory and superstring theory.[53–57]Besides these theoretical extensions,it is also more realistic to experimentally implement the knot lattice model by a network of optical fibers,in which spinning photons demonstrate the optical spin Hall effect.[58]This optical network may provide a different approach to topological quantum computation[2]by constructing braiding on graphene.[59,60] [1]Kitaev A Y 2003 Ann.Phys.303 2 [2]Nayak C,Simon S H,Stern A,Freedman M and Das Sarma S 2008 Rev.Mod.Phys.80 1083 [3]He J and Kou S P 2016 Chin.Phys.B 25 117310 [4]Moore G and Read N 1991 Nucl.Phys.B 360 362 [5]Wilczek F 1982 Phys.Rev.Lett.49 957 [6]Camino F E,Zhou W and Goldman V J 2005 Phys.Rev.B 72 075342 [7]Wen X G 1991 Phys.Rev.Lett.66 802 [8]Georgiev L S 2009 J.Phys.A:Math.Theor.42 225203 [9]Stern A 2010 Nature 464 187 [10]Kitaev A 2006 Ann.Phys.321 2 [11]Bombin H and Martin-Delgado M A 2008 Phys.Rev.A 77 042322 [12]Lang L J,Cai X M and Chen S 2012 Phys.Rev.Lett.108 220401 [13]Hu H P,Cheng C,Luo H G and Chen S 2015 Sci.Rep.5 8433 [14]Hu H P,Cheng C,Xu Z H,Luo H G and Chen S 2014 Phys.Rev.B 90 035150 [15]Hermanns M,Kimchi I and Knolle J 2018 Ann.Rev.Condens.Matter.Phys.9 17 [16]Witten E 1989 Commun.Math.Phys.121 351 [17]Duan Y S,Liu X and Fu L B 2003 Phys.Rev.D 67 085022 [18]Yang C N 1952 Phys.Rev.85 808 [19]Wu F Y 1992 Rev.Mod.Phys.64 1099 [20]Murthy G and Shankar R 2003 Rev.Mod.Phys.75 1101 [21]Jain J K 1989 Phys.Rev.Lett.63 199 [22]Pohl W 1968 J.Math.Mech.17 975 [23]Zhang S C,Hansson T H and Kivelson S 1989 Phys.Rev.Lett.62 82 [24]Qi X L,Hughes T and Zhang S C 2008 Phys.Rev.B 78 195424 [25]Soret M and Ville M 2015 arXiv:1507.00880v1[math.GT] [26]Bogle M G V,Hearst J E,Jones V F R and Stoilov L 1994 J.Knot Theory and Ramilcations 3 121140 [27]Nash C and Sen S 1983 Topology and Geometry for Physicis(Academic Press) [28]Bernevig B A and Zhang S C 2006 Phys.Rev.Lett.96 106802 [29]Konig M,Wiedmann S,Brune C,Roth A,Buhmann H,Molenkamp L W,Qi X L and Zhang S C 2007 Science 318 766 [30]Tsuei C C and Kirtley J R 2000 Rev.Mod.Phys.72 969 [31]Duan Y S 1984 SLAC-PUB-3301 [32]Adams C 2001 The knot book,American Mathematical Society [33]Kasteleyn P W 1963 J.Math.Phys.4 287 [34]Fendley P,Moessner R and Sondhi S L 2002 Phys.Rev.B 66 214513 [35]Scalapino D J 2012 Rev.Mod.Phys.84 1383 [36]Sachdev S 1999 Quantum phase transitions(Cambridge:Cambridge University Press) [37]Zhang G and Song Z 2015 Phys.Rev.Lett.115 177204 [38]Paddison J A M,Ong H S,Hamp J O,Mukherjee P,Bai X,Tucker M G,Butch N P,Castelnovo C,Mourigal M and Dutton S E 2016 Nat.Commun.7 13842 [39]Feng X Y,Zhang G M and Xiang T 2007 Phys.Rev.Lett.98 087204 [40]Chen H D and Nussinov Z 2008 J.Phys.A 41 075001 [41]Si T and Yu Y 2008 Nucl.Phys.B 803 428 [42]Si T 2012 arXiv:1205.1052v4[quant-ph] [43]Yao H and Kivelson S A 2007 Phys.Rev.Lett.99 247203 [44]Yang S,Zhou D L and Sun C P 2007 Phys.Rev.B 76 180404 [45]Haldane F D M 1988 Phys.Rev.Lett.61 2015 [46]Yang S,Gu Z C,Sun K and Das Sarma S 2012 Phys.Rev.B 86 241112 [47]Kane C L and Mele E J 2005 Phys.Rev.Lett.95 226801 [48]Yu H L,Zhai Z Y and Bian X T 2016 Chin.Phys.Lett.33 117305 [49]Qi X L and Zhang S C 2011 Rev.Mod.Phys.83 1057 [50]Hasan M Z and Kane C L 2010 Rev.Mod.Phys.82 3045 [51]Si T 2005 J.Math.Phys 46 122301 [52]Zhang S C and Hu J P 2001 Science 294 823 [53]Marino M 2005 Rev.Mod.Phys.77 675 [54]Dilao R and Schiappa R 1997 Phys.Lett.B 404 57 [55]Babaev E 2002 Phys.Rev.Lett.88 177002 [56]Faddeev L and Niemi A J 1997 Nature 387 58 [57]Si T 2005 JHEP 07 060 [58]Bliokh K Y,Niv A,Kleiner V and Hasman E 2008 Nature Photonics 2 748 [59]Xu H and Wan X 2008 Phys.Rev.A 78 042325 [60]Hu Z X,Bhatt R N,Wan X and Yang K 2011 Phys.Rev.Lett.107 236806

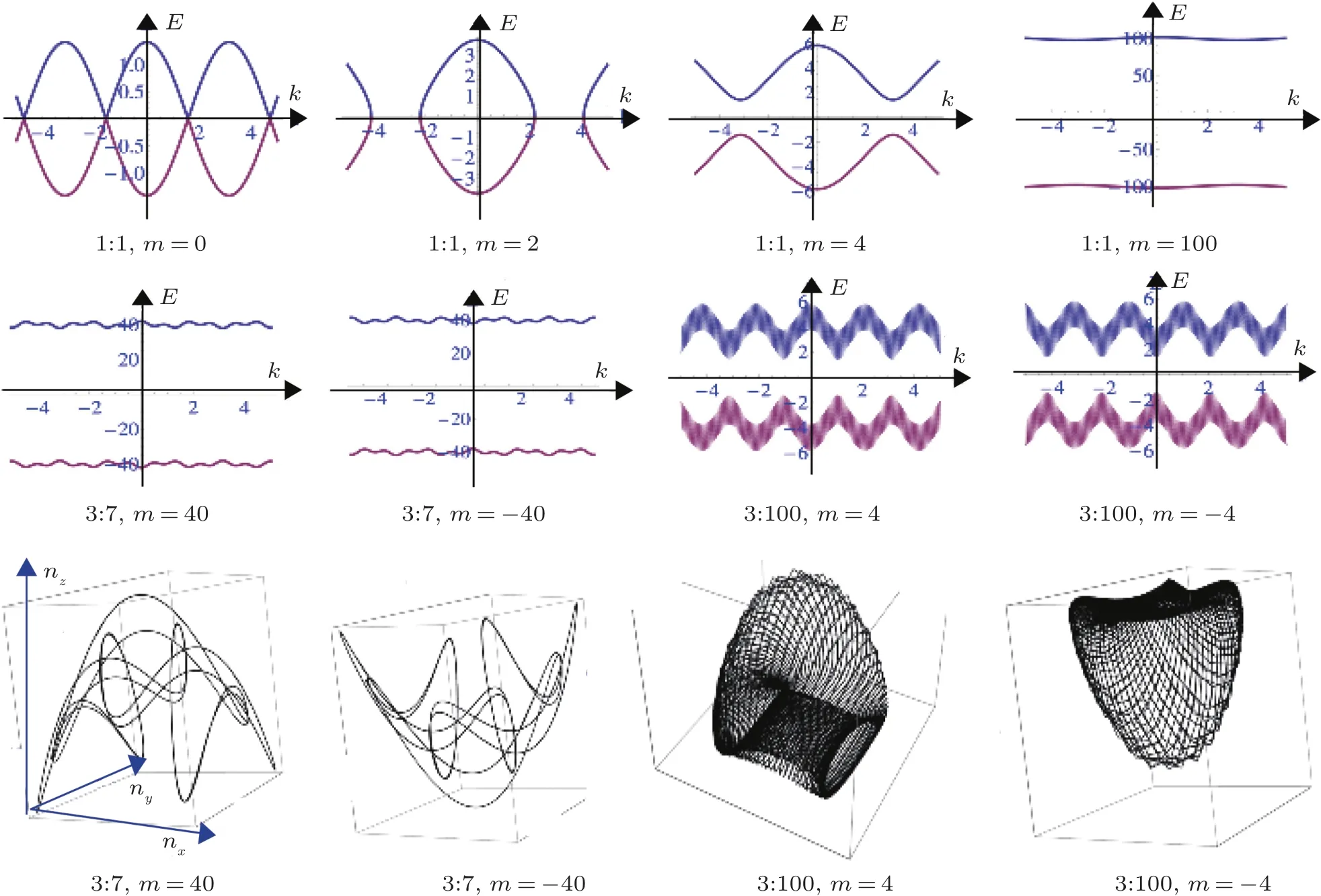



2.5.The long-range fermion pairing model on knot square lattice














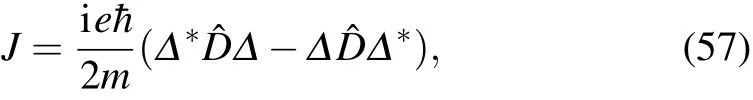





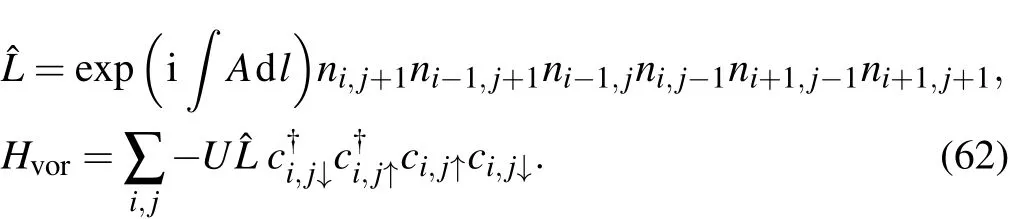
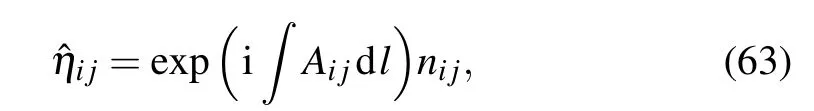



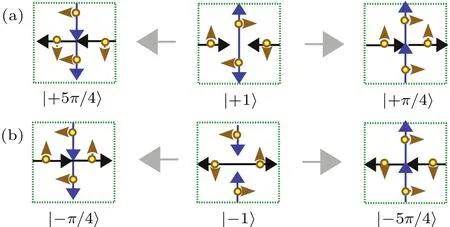
3.Anyons of quantum knot lattice model on honeycomb lattice

3.1.The knot lattice model of transverse- field Ising chain model

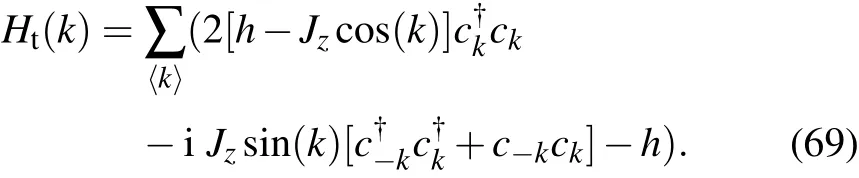
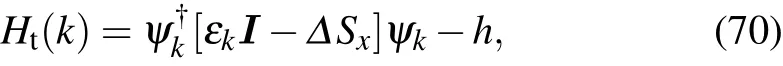


3.2.The knot lattice of spin-1/2 Ising model on honeycomb lattice


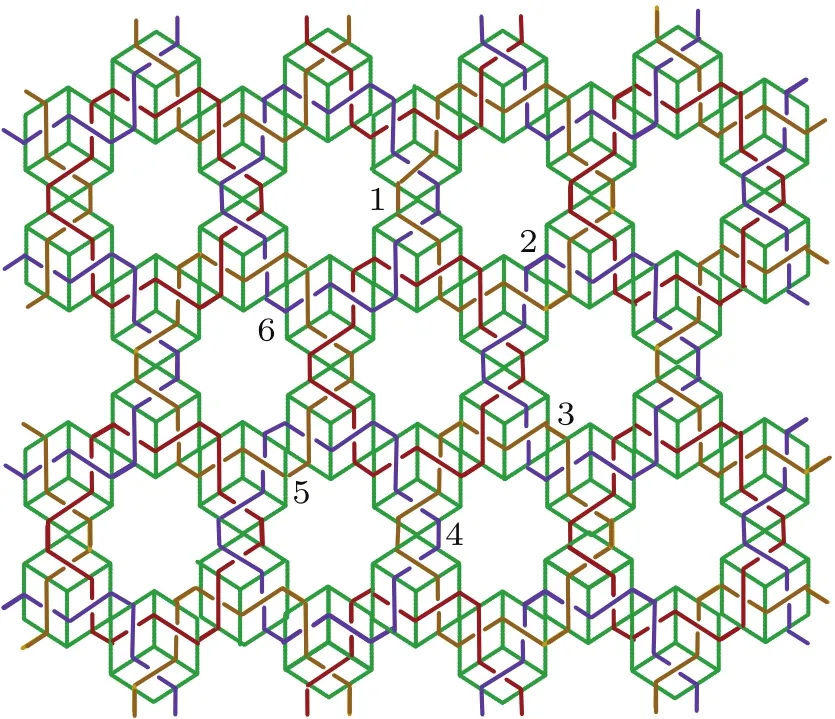


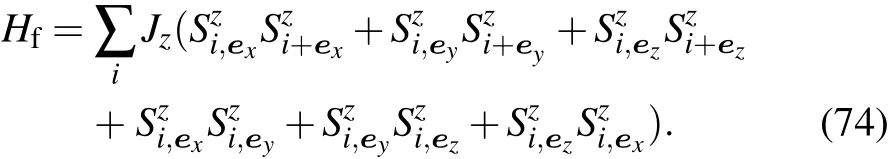
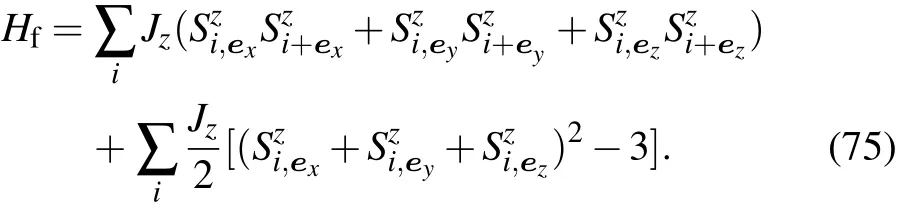
3.3.The knot lattice of spin-1/2 Kitaev honeycomb lattice model

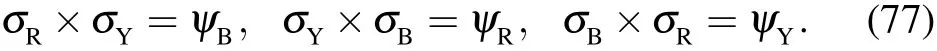










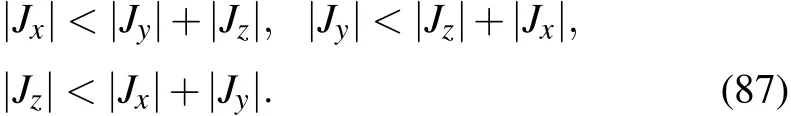

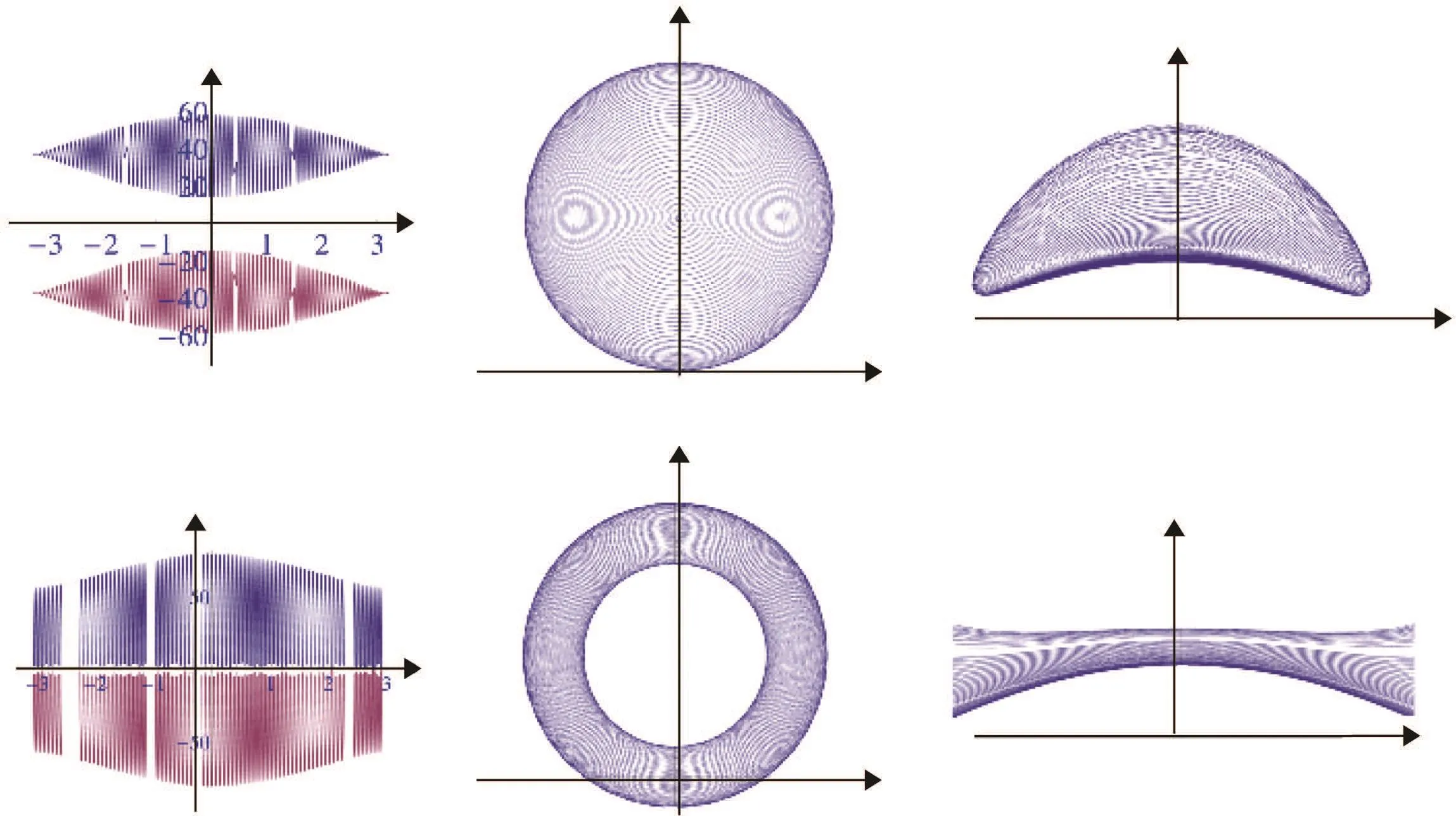
3.4.The gapless edge current of non-Abelian anyon in a finite knot lattice

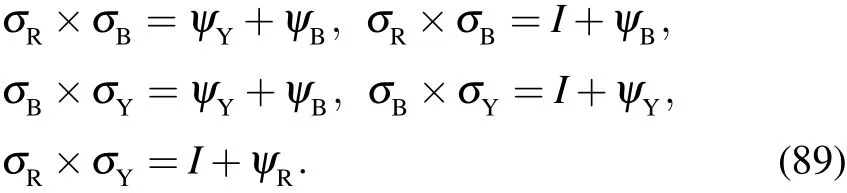

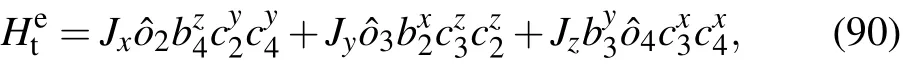
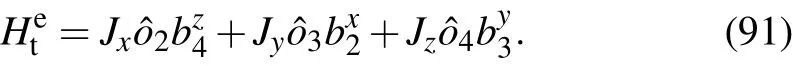

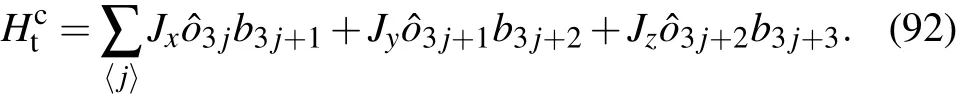


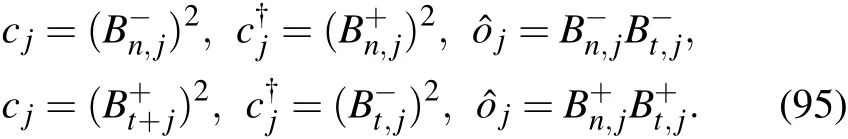



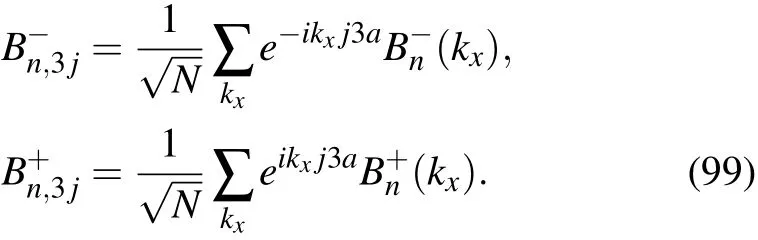

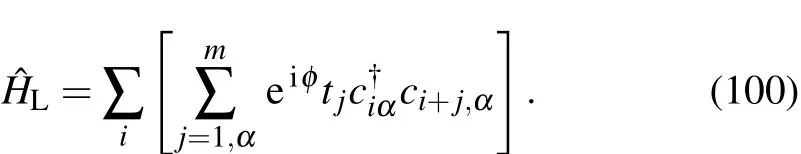


3.5.Knot lattice implementation of quantum lattice model with quantum Hall states
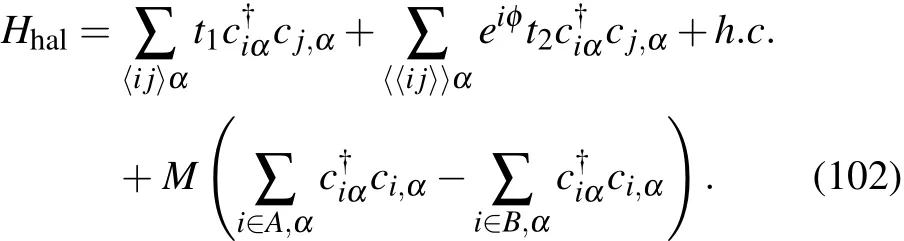


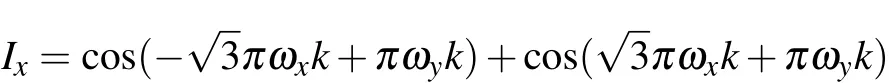





4.Conclusion
杂志排行
Chinese Physics B的其它文章
- Miniature quad-channel spin-exchange relaxation-free magnetometer for magnetoencephalography∗
- Observing the steady-state visual evoked potentials with a compact quad-channel spin exchange relaxation-free magnetometer∗
- Quantum interferometry via a coherent state mixed with a squeezed number state∗
- Cavity enhanced measurement of trap frequency in an optical dipole trap∗
- 7.6-W diode-pumped femtosecond Yb:KGW laser∗
- Anisotropic stimulated emission cross-section measurement in Nd:YVO4
