基于边信任度的混合参数自适应重叠社区发现算法
2019-04-13顾春妹赵建军洪文兴徐文静
汪 清,顾春妹,赵建军,崔 鑫,洪文兴,徐文静
基于边信任度的混合参数自适应重叠社区发现算法
汪 清1,顾春妹1,赵建军1,崔 鑫1,洪文兴2,徐文静2
(1. 天津大学自动化与信息工程学院,天津 300072;2. 厦门大学航空航天学院,厦门 361005)
网络中的社区结构有助于简化网络拓扑结构分析,揭示系统内部的规律,能够为信息推荐和信息传播控制提供有力的支撑.网络重叠社区结构与真实生活更加接近,但其分析较非重叠社区结构更加困难.因此,针对重叠社区发现问题,在对网络的边进行峰值聚类的基础上提出了一种基于边信任度的混合参数的自适应重叠社区发现算法.定义了网络边的邻居边集合及与其邻居边之间的信任度函数,通过信息传递获取边的总信息量,并且基于此引入混合参数的概念.基于k-means算法使用混合参数对网络中的边进行聚类,即将网络中的边划分为核心边集与非核心边集,每个核心边作为一个聚类中心.根据非核心边到核心边的距离将所有非核心边划分至距离其最近的聚类中心所在社区.再根据网络中边与节点的关系实现重叠节点发现,最终实现重叠社区的发现.该算法的优点是每条边通过独立地完成信息扩散找到社区的结构,相比于传统的峰值聚类算法,不需要人为设置相关参数,实现重叠社区的自适应发现.为验证算法的可行性,对算法复杂度进行了分析,并且使用两种社区划分评价指标——标准化互信息和模块度,分别在人工数据集及6种真实数据集上进行实验,通过与其他算法进行对比分析,实验结果表明该算法更具可行性和有效性.
峰值聚类;边信任度;混合参数;重叠社区发现;自适应算法
网络与我们的日常生活息息相关,如交通系统、通信系统和社交网络等.众所周知,社区在揭示网络隐藏结构方面发挥着重要作用,并且现实问题中节点可能属于多个社区,这些节点称为重叠节点.如果社区包含重叠节点,则称该社区为重叠社区.重叠社区在现实世界中很常见,如一个人可能对几个主题感兴趣并加入多个社交圈,即重叠的社交网络.网络的重叠社区结构很好地反映了真实的网络结构.研究重叠社区结构具有重要的现实意义,不仅有助于揭示复杂系统的内部规则,理解拓扑结构,而且能简化网络分析.但是,由于网络中的节点具有多重身份,使得获得准确的社区结构的难度加大.因此,重叠社区发现已成为该领域中广泛研究的问题,其主要目的是识别由内部密集连接的节点和外部稀疏连接的节点组成的社区.
Chen等[1]于2016 年基于密度峰值聚类和节点局部信息提出一种线性复杂度的社区发现算法. Huang等[2]提出了一种基于密度峰值法的重叠检测算法,并获得了良好的性能.Zhou等[3]利用蚁群算法和标签传播检测重叠社区.该算法首先初始化节点标签和蚂蚁的位置,再按照预先设置的概率进行随机游走并更新节点的标签.当满足条件后,对网络节点所含的标签序列进行处理并为节点分配标签,从而完成网络的重叠社区发现.上述社区发现算法本质上是对网络中的节点进行分类,但是仅仅对节点集进行划分并不能获得网络的重叠社区.因此,相关学者将网络中的边当作数据对象进行聚类研究,即将边分配到不同的社区完成社区发现.Ahn等[4]提出的算法计算了每对边缘之间的相似度,然后使用具有相似性的层次聚类来确定边缘属性由于是层次聚类,因此算法可得到不同分辨率下的社区结构.Shi等[5]基于遗传算法对网络中的边进行聚类,针对网络边定义网络社区结构的基因表达以及交叉和变异算子,从而得到网络的重叠社区.Zhang等[6]在标签传播算法(label propagation algorithm,LPA)的基础上引入边缘聚类系数用于更新标签,而不是随机地进行邻居节点标签的更新,有效地抑制了标签的随机传播,但该算法仅能用于非重叠社区结构及小规模重叠社区的网络,并且不能达到自适应.
本文从边的角度出发,利用网络比边与点之间的关系,提出了一种基于边信任度的混合参数(mixing parameter with trust degree of edge clustering,MPTD-EC)自适应重叠社区发现算法.该算法自动选择核心边,引入边之间信息传递,利用边的总信息量代替峰值聚类中密度,不需要人为地设置截断距离.
本算法不需要人为设定参数,实现了自适应.为了评估提出的方法,将其应用于合成和真实网络.实验结果证明了该算法的有效性.
1 基于边信任度的混合参数自适应重叠社区发现算法
首先,定义邻居边之间的信任度函数,在网络中进行边信息传递获得边信息矩阵,在此基础上计算出边距离矩阵.然后进行核心边的选取,根据边距离矩阵将非核心边进行分配,获得边社区,再将其转换为网络重叠社区.
1.1 信息扩散
利用信息扩散,可以获得每条边的信息量,利用边的信息量去标识边在网络中的重要程度.


(1)

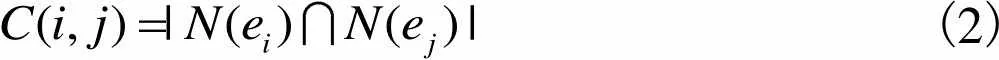
(2)

(3)
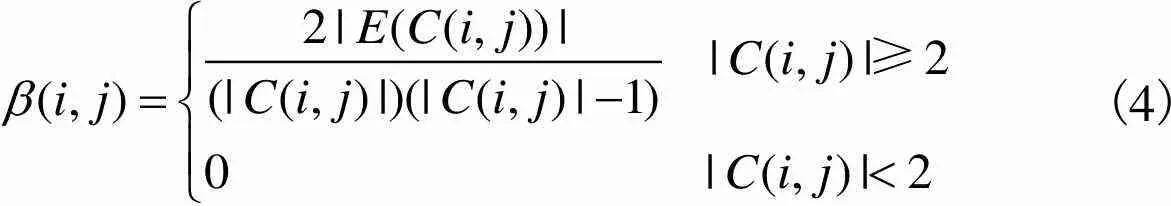
(4)
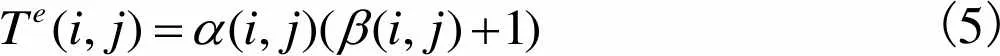
(5)
步骤2遍历网络中的边,每条边依次作为信息源,将其原始信息1用广度优先算法扩散到网络所有边,且当以该边为信息源时,并不考虑其他边所含信息量的大小.
在本算法中,用边的总信息替换峰值簇中每个节点的密度,以避免选择截止距离.
1.2 核心边获取
本文利用改进的k-means算法进行核心边选取.通过获取核心边可以获取整个网络社区的核心集及网络所包含的重叠社区的数目.
k-means算法利用质心(不同聚类的中心)来表示不同类别,具体步骤如下.
步骤1随机选取个初始聚类中心.
步骤2计算出剩余边到聚类中心的距离,将每个数据点分配到距离其最近的中心所在类别.
步骤3重新计算个聚类的中心.
步骤4重复步骤2、步骤3,直到聚类中心不再改变.

步骤3根据如下公式重新计算2个聚类的中心.
通过上述方法即可获得核心边集.
1.3 社区划分

1)信息扩散
步骤2据信息矩阵得归一化距离矩阵.

2)核心边的划分
步骤4重复步骤2、步骤3至聚类中心不再改变.
3)非核心边的划分
2 算法的时间复杂度分析
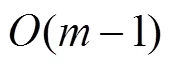
3 评价指标
为了衡量社区发现算法所获社区结构的优劣,提出了模块度[8]、标准化互信息(NMI)等[9]评价指标.研究发现模块度存在分辨率的限制,即网络中较小规模社区结构的存在会造成模块度值很大,但划分的社区结构并非网络的最佳划分.相比模块度,NMI更能评价社区划分的性能.同时因为人工产生的数据集网络本身即重叠社区,使用NMI进行评价.但对于真实数据集,人为将其划分为非重叠社区,因此进行重叠社区划分时,使用NMI并不能衡量算法的性能,因此在真实数据集中,使用改进的模块度进行算法性能的评价.
3.1 标准化互信息
本文通过标准化互信息(NMI)表征本算法在人工网络数据集的性能.NMI通过信息熵来衡量社区发现算法所划分的社区结构和网络已知的社区结构的差异.其计算公式为
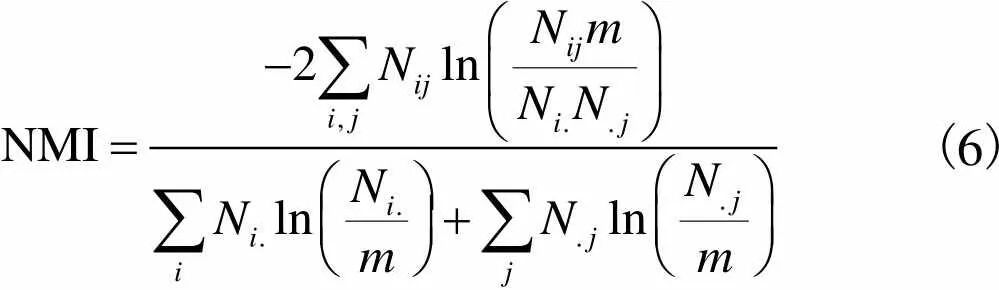
(6)
3.2 基于模块度的改进评价指标
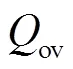

(7)

(8)

(9)

(10)

(11)
4 仿真实验
为了验证本算法的可行性与有效性,分别在合成网络和真实网络上进行了实验,同时将本算法与一些已提出的算法(COPRA[11]和CMP[12])进行了对比 分析.
4.1 人工网络数据集
本文使用LFR模型[13]生成网络,在此基础上进行了分析.由于该模型可通过调整参数控制整个网络和社区属性,如大小、节点度分布、重叠节点数等,合成的网络结构更逼近于真实的社交网络拓扑.
表1 网络参数

Tab.1 Parameters of network
4.2 真实网络数据集
为了进一步测试所提算法,同时在几个经典的经常被用作测试网络的真实社交网络(空手道数据集[14]、Dolphins数据集[15]、Football数据集[16]、Polbooks数据集[17]、Email数据集[18]和PGP数据集[19])上进行实验.这些社交网络的社区结构如表2所示.其中,Email数据集和PGP数据集社区数均为0.
表2 6种真实网络的参数

Tab.2 Parameter of six real networks
4.3 实验结果及分析
4.3.1 人工网络数据集算法性能
在本节中,分别在LFR1、LFR2和LFR3上进行了本算法的性能测试.同时,为了进行比较,在相同的网络上进行COPRA和CMP的测试.实验结果如图1所示.

图1 MPTD-EC算法性能
4.3.2 真实网络数据集算法性能
为了评价本算法性能,实验采用基于模块度的改进评价指标,分别将5种算法应用在6种真实数据集上,数据集相关参数参见表3,实验结果获得6种网络决策图(根据边的总信息量及距离绘制),如图2所示.

图2 MPTD-EC算法在6种真实数据集上获得的决策图
COPRA是随机算法,图3中决策图红点个数表示核心边的个数,即表征了网络中社区的个数.表3中相应的实验结果是50个独立结果的平均值.表3表明本算法在这些社交网络中具有最佳效果,说明本算法的有效性.


Tab.3 Values of obtained by five algorithms
5 结 语
本文在密度峰值聚类的基础上,提出了一种基于边信任度的混合参数自适应重叠社区发现算法.在本算法中,峰值簇中的密度和距离由网络边与边之间的信息传递决定,避免截断距离选取,并且引入混合参数,使用k-means算法进行核心边的选取,从而确定网络社区个数,并且通过边到点的转换完成重叠节点和重叠社区的发现,不需要人为设定相关参数,使算法达到自适应.综合实验结果,可知本算法在人工数据集上较已提出的基于边聚类的社区发现算法更适用于重叠社区数较多的社区发现问题,并且在真实数据集上性能也有较大提升,验证了该算法的可行性和有效性.
[1] Chen Y,Zhao P,Li P,et al. Finding communities by their centers[J]. Scientific Reports,2016,6:24017-1-8.
[2] Huang L,Wang G,Wang Y,et al. A link density cluster ing algorithm based on automatically selecting density peaks for overlapping community detection[J]. International Journal of Modern Physics B,2016,30(24):165-167.
[3] Zhou X,Liu Y,Zhang J,et al. An ant colony based algorithm for overlapping community detection in complex networks[J]. Physica A Statistical Mechanics & Its Applications,2015,427:289-301.
[4] Ahn Y Y,Bagrow J P,Lehmann S. Link communities reveal multiscale complexity in networks[J]. Nature,2010,466(7307):761-764.
[5] Shi C,Cai Y,Fu D,et al. A link clustering based over lapping community detection algorithm[J]. Data & Knowledge Engineering,2013,87(9):394-404.
[6] Zhang X K,Tian X,Li Y N,et al. Label propagation algorithm based on edge clustering coefficient for community detection in complex networks[J]. International Journal of Modern Physics B,2014,28(30):1450216-1-15.
[7] Hu Y,Li M,Zhang P,et al. Community detection by signaling on complex networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2008,78(2):016115.
[8] Clauset A,Newman M E,Moore C. Finding community structure in very large networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2004,70:066111-1-6.
[9] Danon L,Díazguilera A,Duch J,et al. Comparing community structure identification[J]. Journal of Statistical Mechanics Theory & Experiment,2005,2005(9):09008-1-10.
[10] Nicosia V,Mangioni G,Carchiolo V,et al. Extending the definition of modularity to directed graphs with overlapping communities[J]. Journal of Statistical Mechanics:Theory & Experiment,2009(3):3166-3168.
[11] Gregory S. Finding overlapping communities in networks by label propagation[J]. New Journal of Physics,2010,12(10):2011-2024.
[12] Palla G,Derényi I,Farkas I,et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature,2005,435(7043):814-818.
[13] Lancichinetti A,Fortunato S. Benchmarks for testing com munity detection algorithms on directed and weighted graphs with overlapping communities[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2009,80:016118-1-8.
[14] Zachary W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research,1977,33(4):452-473.
[15] Lusseau D. The emergent properties of a dolphin social network[J]. Proceedings Biological Sciences,2003,270(Suppl 2):186-188.
[16] Girvan M,Newman M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences,2002,99(12):7821-7826.
[17] Newman M E J,Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2004,69(2):026113-1-15.
[18] Guimera R,Danon L,Diaz-Guilera A,et al. Self-similar community structure in a network of human interactions[J]. Physical Review E,2003,68(6):065103.
[19] Boguñá M,Pastor-Satorras R,Díaz-Guilera A,et al. Models of social networks based on social distance attacment[J]. Physical Review E,2004,70(5):056122-1-8.
Adaptive Overlapping Community Detection Algorithm Based on Mixing Parameter with the Trust Degree of Edge
Wang Qing1,Gu Chunmei1,Zhao Jianjun1,Cui Xin1,Hong Wenxing2,Xu Wenjing2
(1. School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China; 2. School of Aerospace,Xiamen University,Xiamen 361005,China)
The community structure in a network simplifies the analysis of the network topology,reveals the internal rules of the system,and provides strong support for information recommendation and information dissemination control. The overlapping community structure of the network is closer to real-life scenario,but its analysis is more difficult than the non-overlapping community. Therefore,to solve the overlapping community detection,based on the peak clustering,an adaptive overlapping community detection algorithm based on the mixing parameter with the trust degree of edge is proposed. In this study,the neighbor edge set of the network and the trust function between the edge and its neighbors are defined,and the total information of the edge is obtained through information transfer. Based on this concept,the concept of mixing parameters is introduced. Then,based on the k-means algorithm,clustering is performed using the mixed parameter,i.e.,the edges in the network are divided into a core edge set and a non-core edge set,and each core edge acts as a clustering center. According to the distance from the non-core edge to the core edge,the non-core edges are divided into the community of the nearest cluster center. According to the relation between edges and nodes in the network,overlapping node discovery is achieved. Ultimately the overlapping communities are detected. The advantage of this algorithm is that each edge finds the structure of the community by independently completing information transfer. Moreover,compared to the traditional peak clustering algorithm,the proposed algorithm does not need to set parameters;therefore,adaptive detection of overlapping communities is achieved. To verify the feasibility of our algorithm,the complexity of the algorithm is analyzed. The two evaluation indices of the community detection,normalized mutual information and modularity,are used to experiment on the artificial dataset and the six real datasets respectively. In comparison to other algorithms,the experimental results show that the proposed algorithm is more feasible and effective.
peak clustering;trust degree of edge;mixing parameter;overlapping community detection;adaptive algorithm
10.11784/tdxbz201809051
TN915.01
A
0493-2137(2019)06-0618-07
2018-09-17;
2018-10-15.
汪 清(1982—),博士,副教授,wangq@tju.edu.cn.
洪文兴,hwx@xmu.edu.cn
国家自然科学基金资助项目(61871282);福建省科技计划资助项目(2018H0035);厦门市科技计划资助项目(3502Z20183011).
the National Natural Science Foundation of China(No.61871282),the Science and Technology Program of Fujian,China (No.2018H0035),the Science and Technology Program of Xiamen,China(No.3502Z20183011).
(责任编辑:王晓燕)
