基于人工蜂群的新型圆形交通标志识别算法

董 娜，刘欣宇，吴爱国



基于人工蜂群的新型圆形交通标志识别算法

董 娜，刘欣宇，吴爱国

(天津大学电气自动化与信息工程学院，天津 300072)

道路交通标志检测是智能交通系统的重要组成部分，精确快速识别圆形交通标志对保障交通安全有非常关键的作用．本文将子种群概念引入人工蜂群(artificial bee colony，ABC)算法中，提出了一种基于子种群多峰值优化算法(species-based artificial bee colony，SABC)应用于圆形交通标志的检测．SABC的关键在于多个子种群按照人工蜂群算法同时搜索多个最优解．作为比较，引入了基于子种群的遗传算法(species-based genetic algorithm，SGA)和基于子种群的粒子群优化算法(species-based particle swarm optimization，SPSO)．5个多峰值函数用于验证3种算法的多峰值优化性能，其结果证明SABC具有更高的准确性和更快的运行速度，成功率为100%，精度均低于10-4，运行时间均在0.3s以内．然后，将多圆检测视为多峰值优化问题，并将SABC应用于多圆检测，设计了完整的检测算法．最后，在德国交通标志数据集(German traffic sign recognition benchmarks，GTSRB)的圆形交通标志上测试所提出的圆形检测算法．实验结果表明，所提算法能够以良好的性能定位圆形交通标志．

人工蜂群算法；多峰值优化；子种群；圆形检测；交通标志检测

近年来，随着社会和经济的发展汽车数量不断增加，交通事故的发生频率也越来越高．驾驶安全和舒适便利已经变得越来越重要，驾驶辅助系统(DAS)吸引越来越多计算机视觉和智能交通研究人员的关注．交通标志的自动检测是DAS的关键组成部分．但是，由于许多因素可能会降低检测系统性能，真实情况下的交通标志检测是一项挑战[1]．计算机视觉技术已被证明可以很好地解决这个问题．目前的检测算法主要从形状分析和颜色分割两个方面进行．诸如Hough变换、径向对称变换、HOG特征等基于形状的算法大多涉及复杂的图像操作，缺乏实时性能；基于颜色分割算法实时性好，但其中大多数使用固定的分割阈值，适应性差[2]．交通标志很多为圆形，而且在常见交通标志以及道路上是指示危险的最重要信号[3]．笔者针对圆形交通标志，提出一种检测算法，并使用德国交通标志数据集(GTSRB)测试该算法的性能．

圆形检测问题已被广泛研究．大多数检测算法可以分为两类：基于霍夫变换的技术和最小二乘法[4].尽管两种算法都有很多改进[5-10]，但仍存在以下问题：基于霍夫变换的算法存在计算成本与精度之间的矛盾，而基于最小二乘法的算法鲁棒性低．而且，这两种算法在多圆检测很少被研究．实际上，多峰值优化问题可以很好地解决多圆检测问题[5]．目前很多基于群智能算法已经被提出以解决多峰值优化问题[11-16]．但大多数算法仍存在寻优精度低，成功率不高、运行时间长的缺点．于是，子种群的概念被引入群智能算法以实现多峰值优化[11,16]．

2005年，受到蜂群通过分工和信息交换合作获取蜂蜜的想法启发，土耳其学者Karaboga[16]提出了人工蜂群(artificial bee colony，ABC)算法．ABC具有收敛速度更快、控制参数更少、搜索精度更高、鲁棒性更强、操作更简单等优点[17-19]．

划分子种群的技术被证明是一种解决多峰值优化问题很好的算法[11,20]．因此本文将子种群的概念引入ABC中，提出一种基于子种群的人工蜂群(SABC)算法，用于解决多峰值优化问题，并应用于多圆检测．算法包括2个关键步骤：①将种群划分为子种群；②每个子种群内部按照人工蜂群算法独立迭代搜索．步骤①是实现多峰值优化的关键点．

1 人工蜂群算法

蜂群采蜜过程涉及蜜源、引领蜂、跟随蜂和侦察蜂共4个组成要素，以及招募蜜蜂和放弃蜜源2种基本的行为[17-18]．

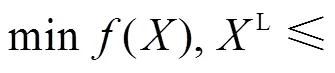
1) 种群初始化

 (1)

2) 引领蜂搜索

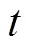
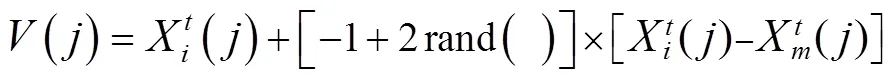
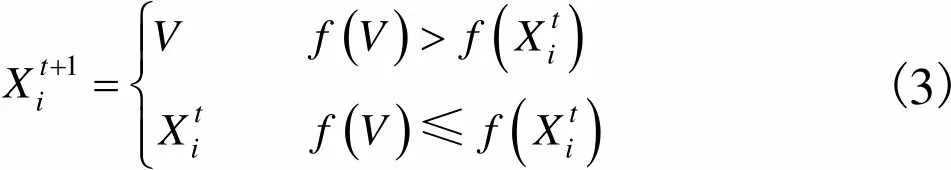
(3)

3) 跟随蜂搜索

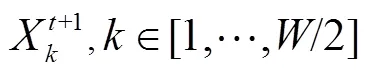
 (4)

4) 侦察蜂搜索

人工蜂群算法模拟蜜蜂采蜜过程中侦察蜂搜索新蜜源的生理行为，提出侦察蜂搜索方式．假设某一个体在一个位置连续停留Bas()次，＝1，2，…，，且Bas()大于设定停留值Limit，则认为其周围搜索到优质蜜源的可能较小，则该个体转换为侦察蜂，按式(1)搜索产生新个体，并与原个体按式(3)进行比较，择优保留个体．

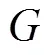
2 基于子种群的人工蜂群算法SABC

多峰值优化是指找到搜索空间内函数的所有最优值，这种优化受到了研究人员的广泛关注．很多相关的算法已经被提出，一种基于子种群的粒子群优化算法(SPSO)[11,20]被提出用来解决多峰值优化问题．目前，人工蜂群算法在多峰值优化问题解决上的研究较少，本文将子种群的概念引入人工蜂群算法中，提出一种基于子种群的人工蜂群算法来解决多峰值的优化问题．

2.1 子种群

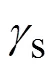
子种群划分步骤如下．

步骤1 计算所有个体的适应度值，并按照从优到劣的顺序重新排序．

步骤2 找到适应度值最优的个体作为第1个子种群的种子．

步骤4 重复步骤3直到所有个体都分完．

2.2 基于子种群的人工蜂群算法

以一个具有4个全局最优值的多峰值函数寻优过程为例，说明SABC算法原理，如图1所示．

图1 SABC迭代原理

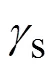
SABC的关键思想是“先分群后分蜂”，即先将大种群分为若干个子种群，再对每个子种群分3种蜂进行搜索．首先按式(1)初始化种群，然后对所有个体按照第2.1节中的算法划分子种群并确定种子．对于每个子种群，先计算其适应度函数值，根据适应度值大小将其分为引领蜂、跟随蜂和侦查蜂3种：引领蜂按照式(2)局部搜索新蜜源并计算出新蜜源的适应度函数值，比较适应度值，按式(3)择优保留，并注意更新停留次数；跟随蜂依概率式(4)在新的引领蜂种群中选择较优目标个体与随机选择的个体按式(2)进行搜索，产生新个体，比较并保留最优位置，更新停留次数，形成跟随蜂种群；判断个体是否放弃当前蜜源位置成为侦察蜂搜索下一蜜源，是则按照式(1)在解空间随机产生新蜜源．

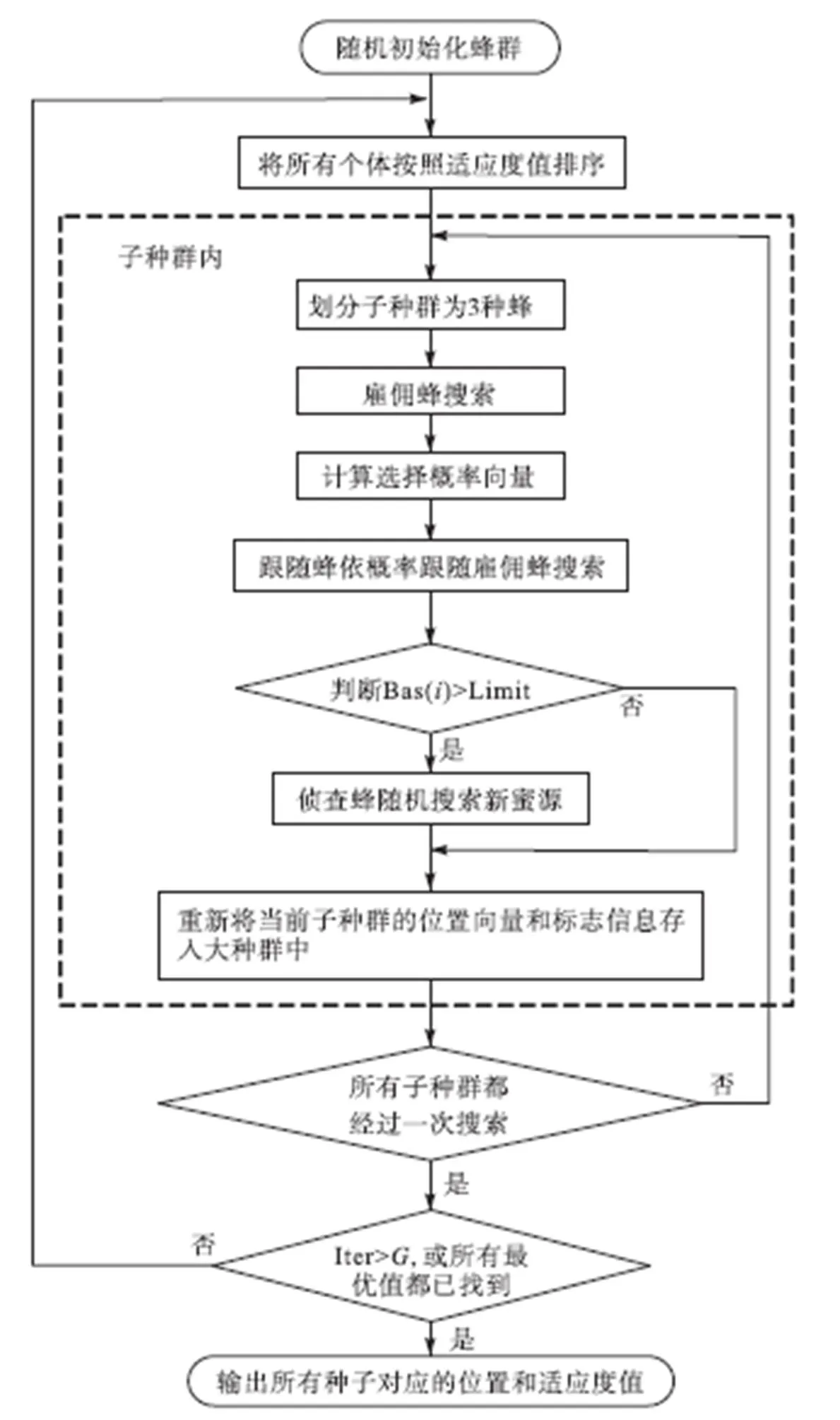
图2 SABC算法流程

最后将当前子种群更新后的位置及个体所对应的停留次数重新存入种群，为下一次迭代做好准备．所有子种群完成一次迭代后重新划分子种群开始下一次迭代．

2.3 SABC算法性能测试

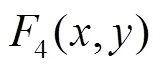
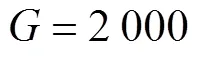
表1 标准测试函数

Tab.1 Standard test functions

整体来说，比较3种算法的优化误差，SABC得到的最优值误差最小，最接近理论值，也是最稳定的．在优化过程中，种群中的所有个体将逐渐聚集为与函数最优值个数相等的子种群．

经过实验和比较，可以得出结论：本文所提出的SABC算法在多峰值优化问题上具有优异的性能．这是因为ABC算法本身具有很强的全局收敛性，利用跟随蜂贪婪选择引领蜂，加快了算法的迭代速度，同时利用侦查蜂帮助算法跳出局部最优，增加解的多样性，在此基础上引入子种群，在子种群内部分开搜索，加速了多峰值函数的优化．

表2 测试函数优化结果

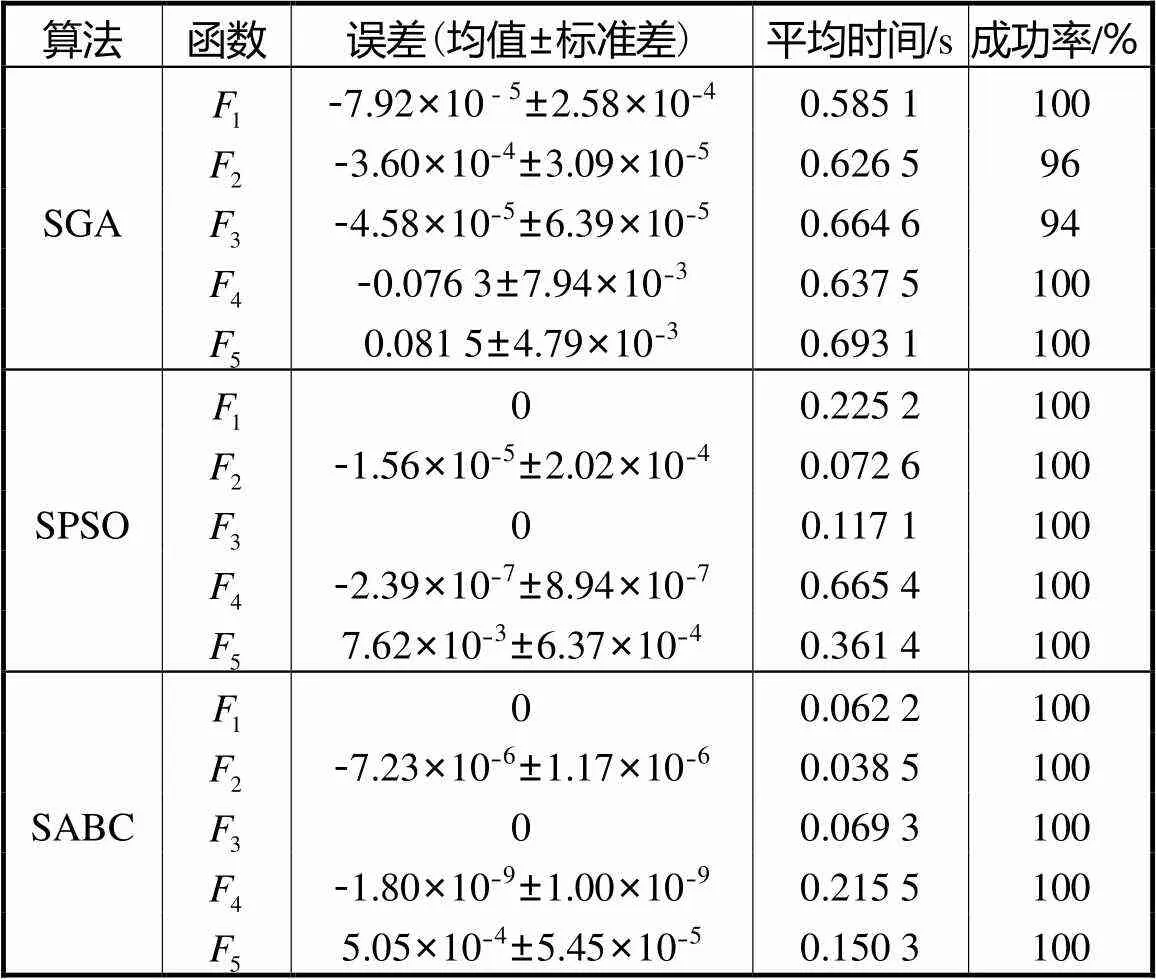
Tab.2 Optimizationresults of benchmark functions

注：成功率表示50次实验中成功找到所有最优值的百分比．

3 SABC在圆形探测上的应用

本节将提出的新型SABC算法应用到了圆形探测问题中，通过3个边缘点来定位一个圆的3点法，这种算法通过公式推导能够巧妙地将圆对应群智能优化算法中的一个个体．

3.1 圆的表示及适应度评估

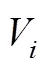
 (5)

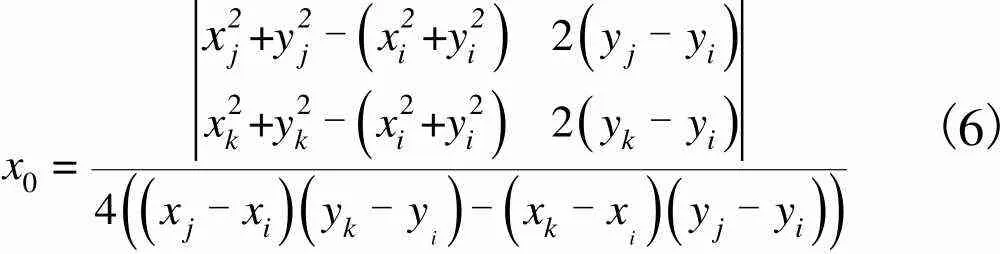
 (6)

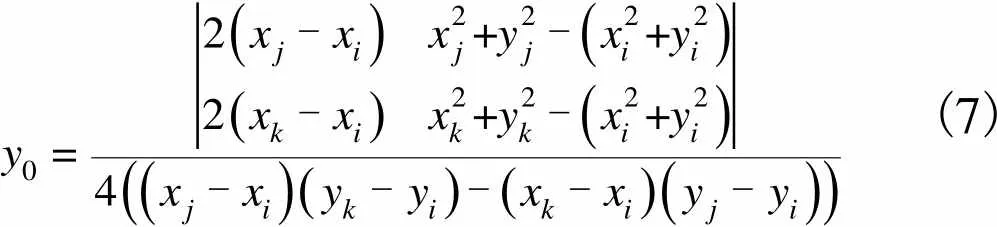
 (7)

 (8)

 (9)

 (10)

 (11)

所提出的基于SABC的多圆检测算法的完整过程如图3所示．

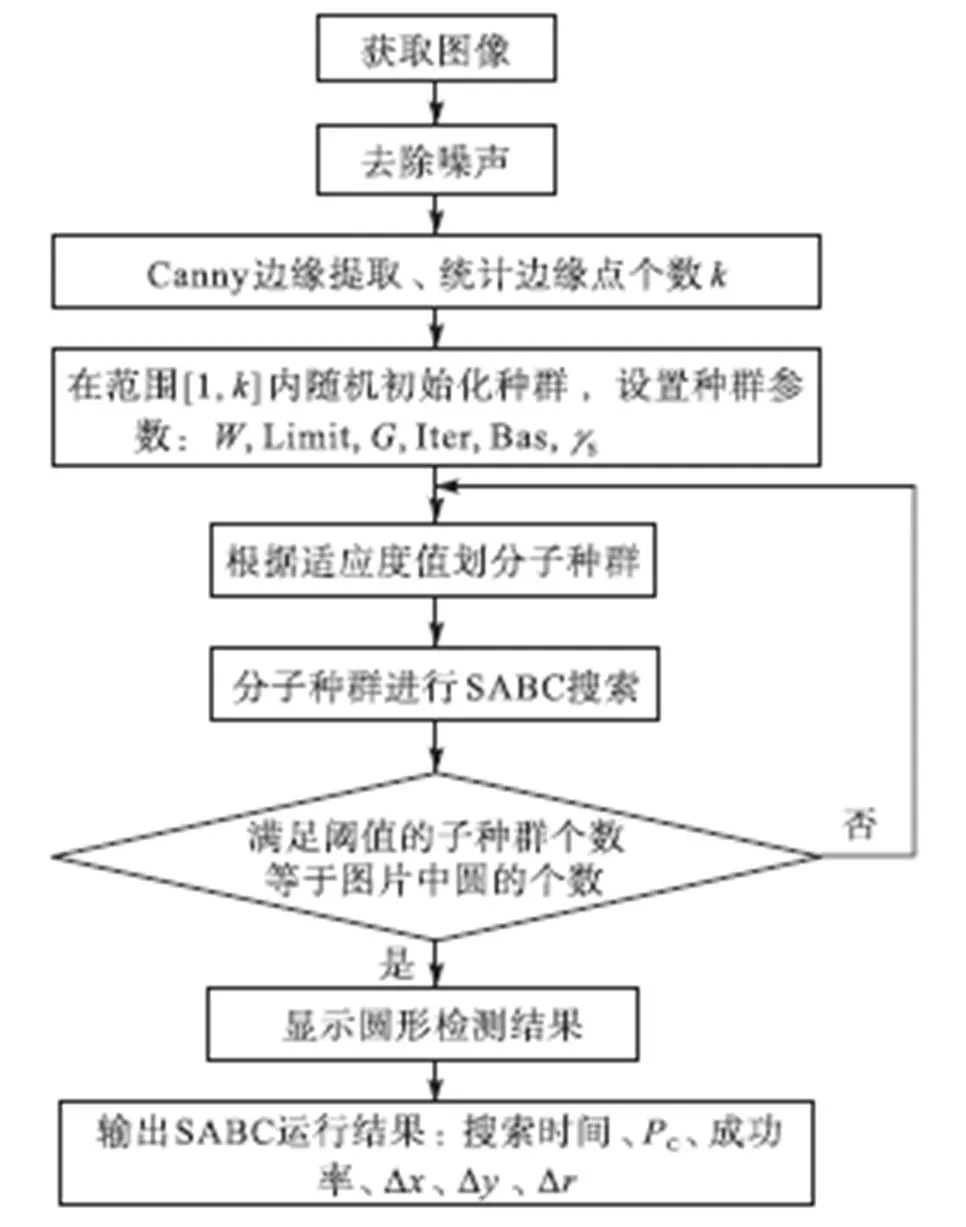
图3 基于SABC的圆形检测算法

3.2 仿真测试

首先选择了一幅有6个随机分布圆形的测试图像来测试所提出的多圆检测算法的性能．子种群中两个个体之间的距离被定义为与两个个体相对应圆的圆心之间的距离．测试图像中圆的数量和圆之间的距离是已知的，子种群半径被设置为比两个最近的圆之间的距离稍小一点的值．

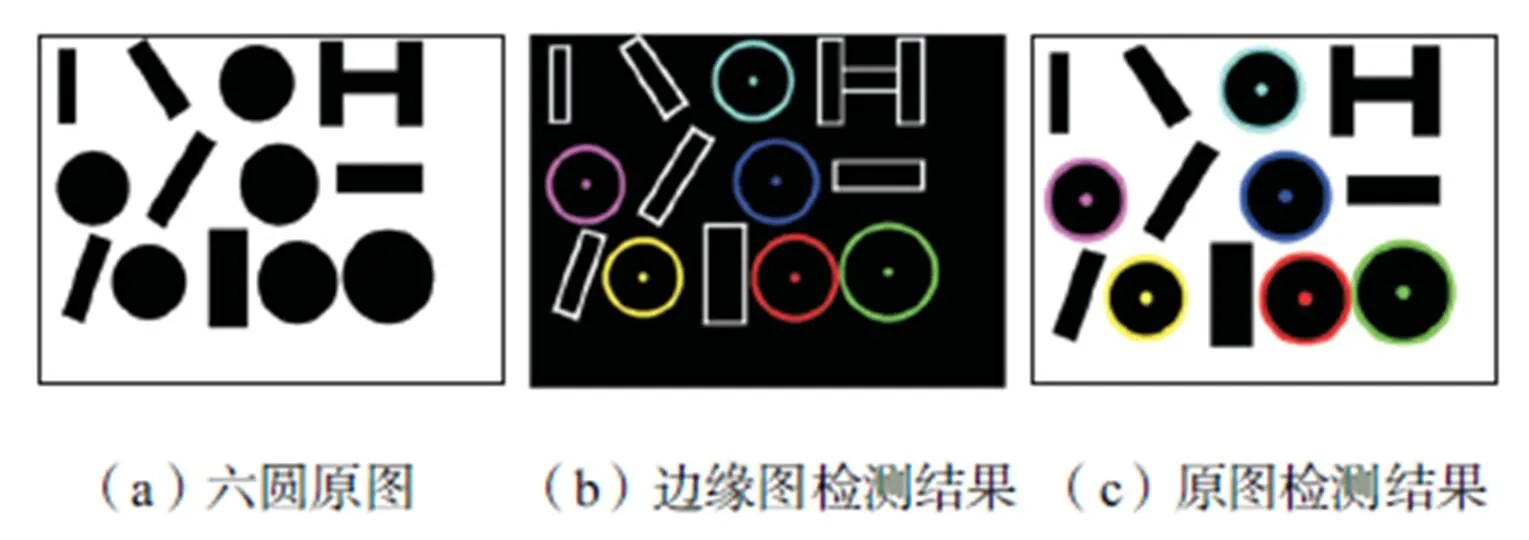
图4 测试图像及测试结果

表3 3种算法对图4独立运行50次的检测结果比较

Tab.3 Comparison of detection results of three algorithms on Fig.4

注：成功率表示50次实验中成功找到所有最优值的百分比.

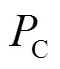
实验结果表明，基于SABC的多圆定位算法成功率高，精确度高，计算时间短，SABC的多峰值优化性能可以很好地应用于多圆检测，且优势明显．

3.3 SABC对圆形交通标志检测

在本节中，将SABC应用于圆形交通标志检测，并与SGA和SPSO进行比较．在实验中，使用来自德国的交通标志数据集(GTSRB)中的圆形交通标志来验证SABC的识别性能，GTSRB是用于计算机视觉、模式识别和基于图像的驾驶员辅助领域感兴趣检测评估的德国交通标志数据集，GTSRB包含43类交通标志，如图5所示．

选取其中的圆形交通标志，在偏亮、偏暗、模糊、变形的情况下测试了算法性能．原图和检测结果如图6所示，算法性能如表4所示．

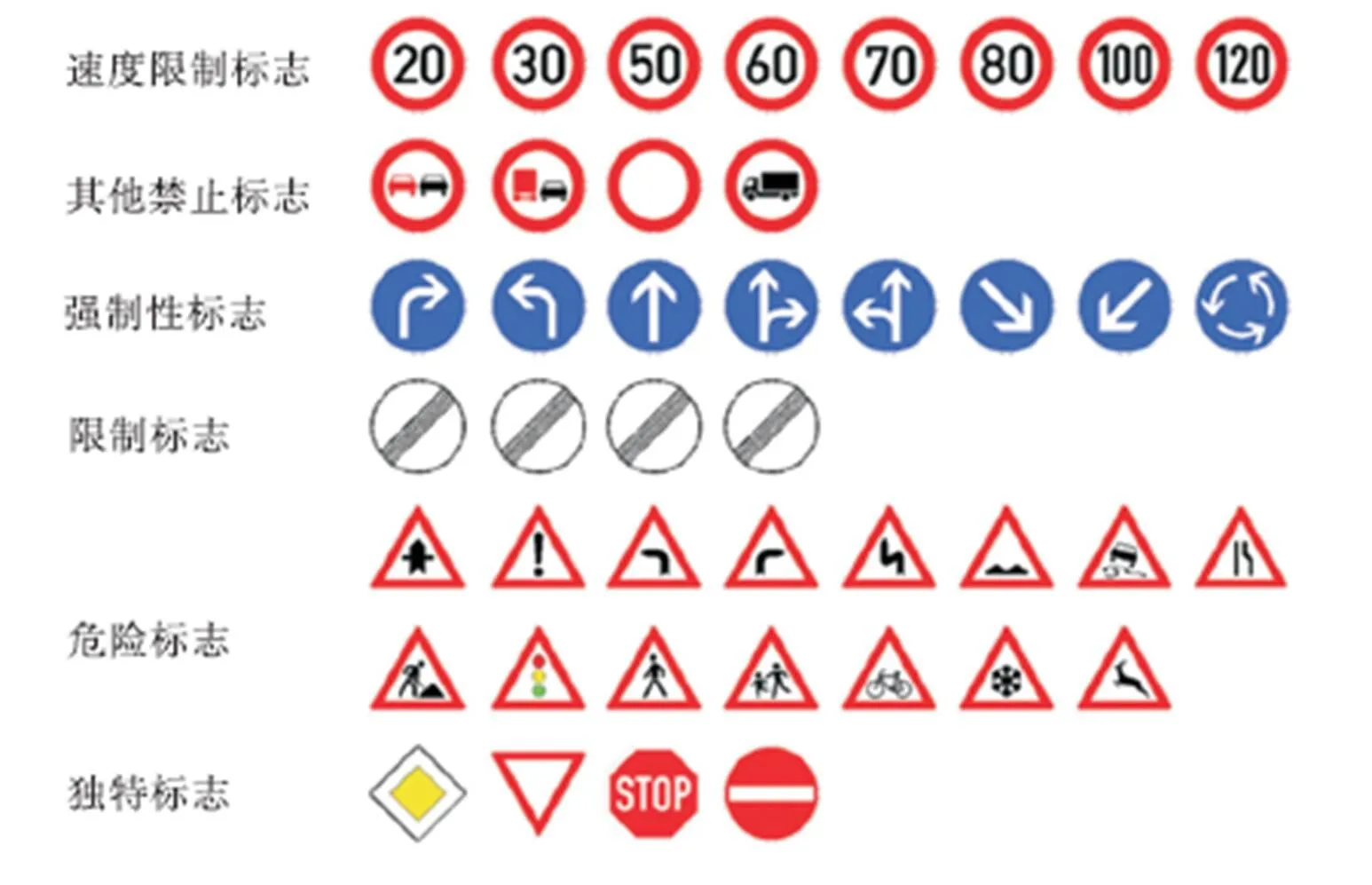
图5 德国交通标志数据集

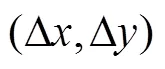
此外，为了检验该算法的性能，又与另外两种不同机理的算法进行了对比实验，文献[21]采用基于RGB固定阈值分割及Hough变换的算法，对标志的检测率为92.83%，时间开销为2.644s．文献[22]采用规格化RGB颜色分割及基于径向对称变换的算法，对标志的检测率为91.40%，时间开销为0.472s．本文算法在检测率和时间开销上都优于以上两种算法，图7为3种算法的检测结果对比．本文算法对GTSRB当中的圆形标志进行大量实验，检测情况见表5，由此可以看出，所提算法对于圆形交通标志牌的检测效果良好．

图6 不同情况下的检测结果

表4 不同算法对图6独立运行50次的仿真结果比较

Tab.4 Comparison of simulation results of different algorithms on Fig.6 for 50 running independently

注：成功率表示50次实验中成功找到所有最优值的百分比.

图7 3种算法检测结果对比

表5 SABC对GTSRB的检测结果

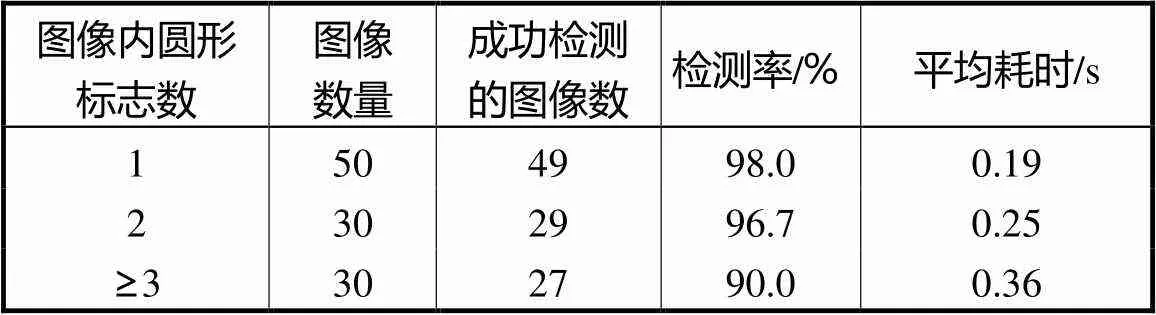
Tab.5 GTSRB detection results of SABC

4 结 语

得益于快速发展的汽车行业、先进的驾驶辅助和自动驾驶系统近年来受到越来越多的关注．自动交通标志检测和识别是这些专家智能系统最重要和最有益的特点．在这些系统的辅助下，安全舒适的驾驶才得以保证．为此，笔者提出了用于圆形交通标志检测和识别的算法，以进一步提高文献中提出的自动交通标志检测和识别算法的性能．

通过引入划入子种群的技术，本文首先提出一种新型优化算法SABC解决了多峰值优化问题．SABC的关键在于多个子种群同时按照ABC算法搜索，经过算法不断迭代最终找到多个最优解．5个标准测试函数首先对SGA、SPSO与SABC的多峰值优化性能进行测试并比较，结果证实SABC在多峰值优化上保留了原始ABC算法搜索精度高、搜索时间快、控制参数少的优点，同时在多个最优解搜索上成功率较高，在解决多峰值优化问题上优势明显．之后通过将多圆检测转化为多峰值优化问题，设计了基于SABC完整的多圆检测算法．进一步地，将所提出的多圆检测算法应用于圆形交通标志检测，并在德国交通标志数据集中的圆形交通标志上进行多次实验，通过与其他算法对比，显现出基于SABC的多圆检测算法在圆形交通标志检测上具有更好的性能．

由于移动设备的处理能力和资源增加，所提出的多圆检测算法也可以用于其他专家和智能系统中，检测或识别交通标志以外的圆形物体．

［1］ Li H，Sun F，Liu L，et al. A novel traffic sign detection method via color segmentation and robust shape matching[J]. Neurocomputing，2015，169：77-88.

［2］ Berkaya S K，Gunduz H，Ozsen O，et al. On circular traffic sign detection and recognition[J]. Expert Systems with Applications，2016，48：67-75.

［3］ 李迎松，郑顺义，夏远鑫，等. 自然环境下圆形禁令交通标志检测[J]. 武汉大学学报：信息科学版，2016，41(12)：1619-1625.

Li Yingsong，Zheng Shunyi，Xia Yuanxin，et al. Circular ban traffic sign detection in natural environment[J]. Journal of Wuhan University：Information Science Edition，2016，41(12)：1619-1625(in Chinese).

［4］ Pan L，Chu W S，Saragih J M，et al. Fast and robust circular object detection with probabilistic pairwise voting[J]. IEEE Signal Processing Letters，2011，18(11)：639-642.

［5］ Dong N，Wu C H，Ip W H，et al. An opposition-based chaotic GA/PSO hybrid algorithm and its application in circle detection[J]. Computers & Mathematics with Applications，2012，64(6)：1886-1902.

［6］ Djekoune A O，Messaoudi K，Amara K，et al. Incremental circle hough transform：an improved method for circle detection[J]. Optik-International Journal for Light and Electron Optics，2017，133：17-31.

［7］ Zhang H，Wiklund K，Andersson M，et al. A fast and robust circle detection method using isosceles triangles sampling[J]. Pattern Recognition，2016，54：218-228.

［8］ Marco T D，Cazzato D，Leo M，et al. Randomized circle detection with isophotes curvature analysis[J]. Pattern Recognition，2015，48(2)：411-421.

［9］ Zelniker E E，Clarkson I V L. Maximum-likelihood estimation of circle parameters via convolution[J]. IEEE Trans on Image Process，2006，15(4)：865-876.

［10］ Frosio I，Borghese N A. Real-time accurate circle fitting with occlusions[J]. Pattern Recognition，2008，41(3)：1041-1055.

［11］ Luo W，Sun J，Bu C，et al. Species-based particle swarm optimizer enhanced by memory for dynamic optimization[J]. Applied Soft Computing，2016，47：130-140.

［12］ 毕晓君，王艳娇. 用于多峰函数优化的小生境人工蜂群算法[J]. 系统工程与电子技术，2011，33(11)：2564-2568.

Bi Xiaojun，Wang Yanjiao. Niche artificial bee colony algorithm for multi-peak function optimization[J]. Systems Engineering & Electronics，2011，33(11)：2564-2568(in Chinese).

［13］ 邓 涛，姚 宏，杜 军，等. 多峰函数优化的改进人工鱼群混合算法[J]. 计算机应用，2012，32(10)：2904-2906.

Deng Tao，Yao Hong，Du Jun，et al. Improved artificial fish swarm hybrid algorithm for multi-peak function optimization[J]. Journal of Computer Applications，2012，32(10)：2904-2906(in Chinese).

［14］ 贾盼龙，田学民. 基于自适应小生境的改进入侵性杂草优化算法[J]. 上海电机学院学报，2012，15(4)：225-230.

Jia Panlong，Tian Xuemin. Improved invasive weed optimization based on adaptive niche algorithm[J]. Journal of Shanghai Dianji University，2012，15(4)：225-230(in Chinese).

［15］ Dong N，Wu C H，Ip W H，et al. Species-based chaotic hybrid optimizing algorithm and its application in image detection[J]. Applied Artificial Intelligence，2014，28(7)：647-674.

［16］ Karaboga D. An Idea Based on Honey Bee Swarm for Numerical Optimization[R]. Turkey：Computer Engineering Department，Erciyes University，2005.

［17］ 秦全德，程 适，李 丽，等. 人工蜂群算法研究综述[J]. 智能系统学报，2014，9(2)：127-135.

Qin Quande，Cheng Shi，Li Li，et al. A review on artificial bee colony algorithm[J]. Journal of Intelligent Systems，2014，9(2)：127-135(in Chinese).

［18］ 张超群，郑建国，王 翔. 蜂群算法研究综述[J]. 计算机应用研究，2011，28(9)：3201-3205.

Zhang Chaoqun，Zheng Jianguo，Wang Xiang. A review of research on bee colony algorithm[J]. Application Research of Computers，2011，28(9)：3201-3205(in Chinese).

［19］ 王艳娇. 人工蜂群算法的研究与应用[D]. 哈尔滨：哈尔滨工程大学通信与信息工程学院，2013.

Wang Yanjiao. Research and Application of Artificial Bee Colony Algorithm[D]. Harbin：School of Communication and Information Engineering，Harbin Engineering University，2013(in Chinese).

［20］ Cai J，Huang P，Chen L，et al. An efficient circle detector not relying on edge detection[J]. Advances in Space Research，2016，57(11)：2359-2375.

［21］ 徐迪红，唐炉亮. 基于颜色和标志边缘特征的交通标志检测[J]. 武汉大学学报：信息科学版，2008，33(4)：433-436.

Xu Dihong，Tang Luliang. Traffic sign detection based on color and boundary feature[J]. Journal of Wuhan University：Information Science Edition，2008，33(4)：433-436(in Chinese).

［22］ Kamada H，Naoi S，Gotoh T. A compact navigation system using image processing and fuzzy control[J]. Southeastcon. Proceedings，1990，1：337-342.

Detection Method for Circular Traffic Signs Based on Artificial Bee Colony

Dong Na，Liu Xinyu，Wu Aiguo

(School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China)

The detection of road traffic signs is an important component of the intelligent transportation system. The accurate and rapid recognition of circular traffic signs plays a crucial role in ensuring traffic safety. In this paper，we introduce the concept of species to the artificial bee colony(ABC)algorithm for the detection of circular traffic signs，and propose a multi-peak optimization algorithm based on a species-based artificial bee colony(SABC). The key idea of the SABC is that multiple species simultaneously search for multiple optimal values specific to each artificial bee colony. We compare the performance of the SABC with those of the species-based genetic algorithm(SGA)and particle-based particle swarm optimization(SPSO)algorithm. Using five multi-peak functions to verify the multi-peak optimization performance of these three algorithms，the results indicate that SABC has higher accuracy and faster running speed. With a success rate of 100%，SABC’s accuracy is within 10-4，and its running time is less than 0.3s. Then，considering multi-circle detection as a multi-peak optimization problem，we applied the SABC to multi-circle detection，and designed a complete detection method. We tested the proposed circular detection method on circular traffic signs with respect to the German Traffic Sign Recognition Benchmark(GTSRB). The experimental results show that the proposed algorithm performs well in locating circular traffic signs.

artificial bee colony(ABC)algorithm；multi-peak optimization；species；circle detection；traffic signs detection

10.11784/tdxbz201808043

TP391.4

A

0493-2137(2019)06-0585-09

2018-08-13；

2018-11-04.

董 娜（1983—），女，博士，副教授.

董 娜，dongna@tju.edu.cn.

国家自然科学基金资助项目(61773282).

the National Natural Science Foundation of China(No.61773282).

(责任编辑：孙立华)