把双曲线化为圆

广东省佛山市乐从中学(528315) 林国红

仿射变换是一种二维坐标到二维坐标的线性变换,变换保持二维图形间的相对位置关系不发生变化: 将平行线变为平行线、直线变为直线、并且同一条直线上的点的位置顺序和长度的比例关系保持不变, 对应直线的斜率比保持不变,以及对应图形的面积比保持不变等等.人教A 版教材选修4-4 中的“伸缩变换”就是仿射变换,同时《普通高中数学课程标准》要求: 了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.

我们知道, 椭圆的问题通常采用二次方程的根与系数的关系或引入参数来求解, 但常常伴随着运算上的繁琐和消参的困难.而圆是特殊的椭圆, 相比椭圆来说更为简单直观, 利用仿射变换可以将椭圆变为圆C :X2+Y2=1,从而把椭圆的问题转化为关于圆的问题,再利用圆的良好的几何性质解决问题,往往使解题过程更简捷.

而双曲线,椭圆与圆都是有心圆锥曲线,椭圆和圆的很多性质可以类比到双曲线中,那么是否有类似于椭圆化“圆”的变换,来把双曲线化为“圆”呢?

一、双曲线化为圆

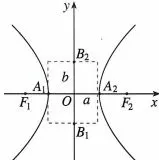
图1

因为y2=−b2有虚根,即y =±bi,也就是说,双曲线和y 轴有两个虚交点,这也是为什么把B1B2叫做虚轴的原因.

同时,在复数中有虚数单位i,满足i2=−1.于是可以在变换中引入虚数单位i,令变换为则双曲线变为“虚圆”X2+Y2=1.

这样的话,就可以利用圆已有的性质去研究双曲线的性质,会给一些双曲线问题的解答带来方便.

二、预备知识

1.复平面上直线方程的复数形式为¯az+a¯z+c=0,其中a 是非零复数,c 是实常数.

证明设z =x+yi,则¯z =x−yi,从而

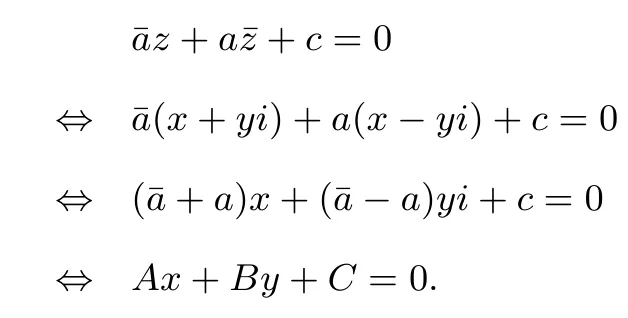
由此可以得到实平面上一些与直线相关的结论,在复平面上仍成立:

(1) 若两条直线l1,l2的斜率为k1,k2,则

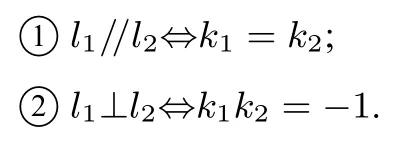
(2) 点P(x0,y0) 到直线Ax+By +C=0 的距离是

2.一元二次方程在复数域上,韦达定理仍成立.

三、双曲线化为圆的应用

解设变换则将双曲线变为圆X2+Y2=1.于是点P(x0,y0)可化为直线AB 在变换后的斜率为kA′B′,则 在 圆X2+Y2=1 中, 有且kA′B′kO′P′=−1, 则又因为所以,

例2求双曲线

解设变换则将双曲线变为圆于是点可化为显然在圆X2+Y2=1 上,所以易得切线方程为即所以双曲线在点处的切线方程为

例3已知双曲线= 1(a > 0,b > 0)上的两点A1(x0,y0), A2(−x0,−y0)关于原点对称, P 是双曲线上的动点,求证: kPA1kPA2为定值.

证明设变换将双曲线变为圆C′: X2+Y2=1,设直线PA1,PA2变换后的斜率为k1,k2,由圆的性质,可知k1k2=−1.又因为所以即故可得为定值.

例4已知双曲线过双曲线外一点P 作双曲线的两条切线,若两条切线相互垂直,求点P 的轨迹方程.

解设变换将双曲线变为圆C′: X2+Y2=1,设变换前两条切线的斜率为k1,k2,变换后两条切线的斜率为由已知,有k1k2=−1,又由所以另设动点P(x,y)变换后的坐标为P′(x0,y0), 过点P′的直线l : y−y0=k′(x−x0),即k′x−y−(k′x0−y0)=0,则圆C′的圆心到直线l 的距离为即(k′x0−y0)2=k′2+1,化简整理,得由韦达定理,有化简得于是由于x=aX,y=bY i,所以点P 的轨迹方程x2+y2=a2−b2.

四、小结

由上述例子可见, 类似椭圆化“圆”, 将双曲线化为“虚圆”,为解决双曲线的问题,提供了新的途径,不仅思路新颖、独特,解答过程简洁,效果事半功倍,而且能引导学生类比、联想、分析和概括,有助于拓展思维空间,提高创新能力.

另外,仿射变换中有很多的变与不变,因仿射的角度不同,每种仿射下的“变”与“不变”也不相同,我们要充分利用“不变”的性质解题,而“变”的性质就决定了椭圆化“圆”后,利用圆的性质解题会有诸多的限制; 同样的, 双曲线化“虚圆”也应利用其中“不变”的性质解题.