空间几何体外接球问题的解题策略*

2019-04-13广东省广州大同中学510545

中学数学研究(广东) 2019年5期

广东省广州大同中学(510545) 袁安

学生解决“空间几何体的外接球”问题较困难,其主要原因是学习的过程中对空间几何体的外接球的概念没有很好的理解,同时对空间几何体外接球的性质没有充分的认识.从而造成了学生解题方法与思路不清,模型的归纳模糊,遇到条件改变或新的背景时,学生没法从概念出发去分析和解决新的问题.笔者通过类比教学,从圆的标准方程及圆的性质定理出发,类比得到球的标准方程及球的性质定理,并类比确定圆心和半径的方法得到确定球心及半径的方法,并对空间几何体的外接球问题进行了模型和方法的归类,从而在本质上帮助学生解决问题.

一、利用类比教学,得到球的方程与性质定理

利用类比教学,引导学生通过类比,根据各自的定义,从平面圆的标准方程类比得到空间球的标准方程.

1.类比得出球的标准方程

平面圆变不变空间球圆的标准方程:(x−a)2+(y−b)2=r2把平面图形“圆”变成空间几何体的“球”动点到定点的距离为定值球的标准方程:(x−a)2+(y−b)2+(z−c)2=R2

2.类比得出球的两个性质定理

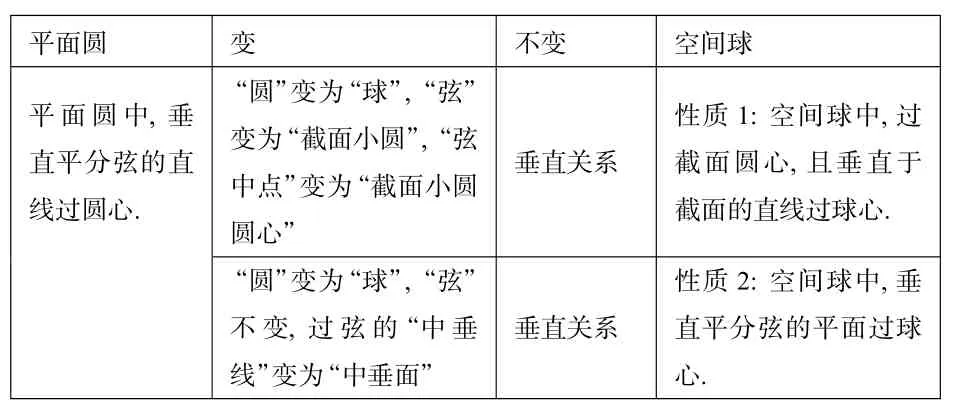
3.类比得出公式

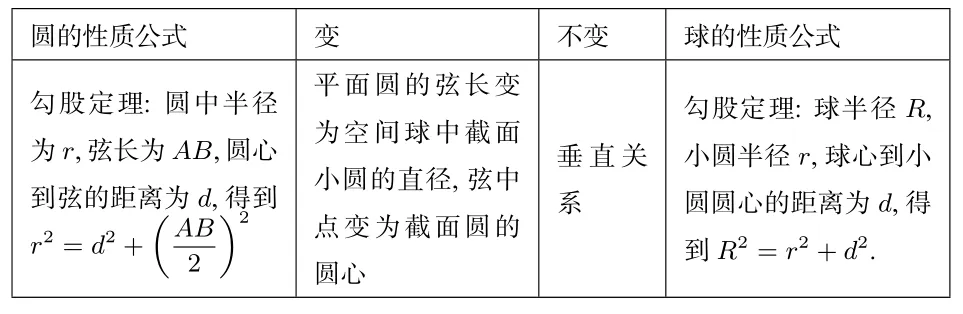
圆的性质公式变不变球的性质公式勾股定理:圆中半径为r,弦长为AB,圆心到弦的距离为d,得到r2=d2+(AB 2)2平面圆的弦长变为空间球中截面小圆的直径,弦中点变为截面圆的圆心垂直关系勾股定理:球半径R,小圆半径r,球心到小圆圆心的距离为d,得到R2=r2+d2.

二、利用性质定理,归纳外接球的模型与解题策略

综合应用上面得到的标准方程和性质定理,可以把几何体的外接球问题归纳为以下四种模型,并针对各自模型找出最佳的方法进行解决.

(一)利用坐标系确定球心坐标

在空间几何体的外接球中,若能较容易的建立空间直角坐标系,写出几何体不共面的四个顶点的坐标,由球的标准方程(x−a)2+(y−b)2+(z−c)2=R2,代入四个点的坐标,建立四个方程,再通过解方程组的代数思想,求出外接球的球心坐标与半径,即可解决问题.

例1三棱锥S−ABC(图1)在空间直角坐标系的坐标是A(0,0,0),B(0,4,0),C(2,6,0),S(2,2,4),求三棱锥S−ABC的外接球半径.

图1

分析本题中有不共面的四个顶点的坐标,特征明显,可以直接通过解方程组求出球心坐标和半径.

解设三棱锥S−ABC外接球方程为(x−a)2+(y−b)2+(z−c)2=R2,代入四个点坐标得

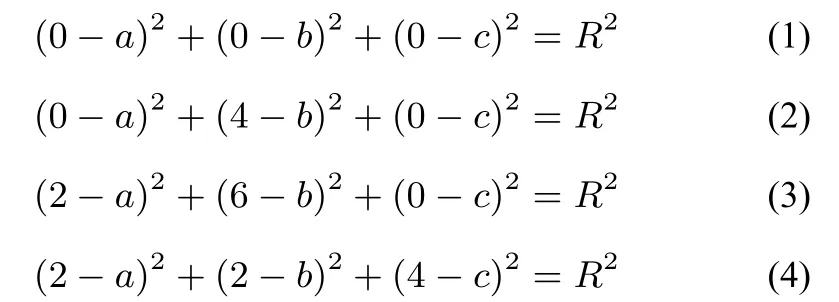
例2三棱锥的P−ABC(图2)的各边长分别是AB=3,AC=4,BC=5,PA=PB=求三棱锥的外接球表面积.

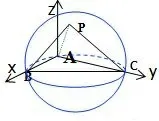
图2

分析由条件可得△ABC为直角三角形,A、B、C三点坐标可以容易得到,又由三条弦长,可以求出P点坐标.如图建立空间直角坐标系,A(0,0,0),B(3,0,0),C(0,4,0),P点坐标为P(x,y,z).由题目可知PA=解得x=2,y=3,z=5,点P坐标为(2,3,5),设三棱锥P−ABC外接球方程为(x−a)2+(y−b)2+(z−c)2=R2,代入得外接球表面积S球=4πR2=4π

此类模型的特点是:空间几何体易建立空间直角坐标系,并能写出空间几何体不共面的四个顶点的坐标,建立方程组,解出球心与半径.这种模型的题目,方法容易掌握,但计算过程较繁杂,对解方程组的要求较高.

(二)利用线面交点确定球心

由前面的图式得到了球的两个性质:(1)球中过截面圆心且垂直于截面的直线过球心;(2)球中垂直平分弦的平面过球心.因此得到结论:过多面体中一个面的外接圆圆心的垂线与一棱的中垂面交点为球心,即利用线与面的交点确定球心.

直棱柱(圆柱)中,上下底面外接圆圆心的连线(垂直上下底面)过球心,又因侧棱(母线)的中垂面过球心,所以球心就是直棱柱(圆柱)的上下底面外接圆圆心的连线的中点.如:正三棱柱(图3),底面边长为a,高为h,底面外接圆半径O1,O2为上下底面的外接圆圆心,则球心O为线段O1O2的中点,则其外接球半径为因此直棱柱(圆柱)的底面外接圆半径r,高为h,则其外接球半径为R=

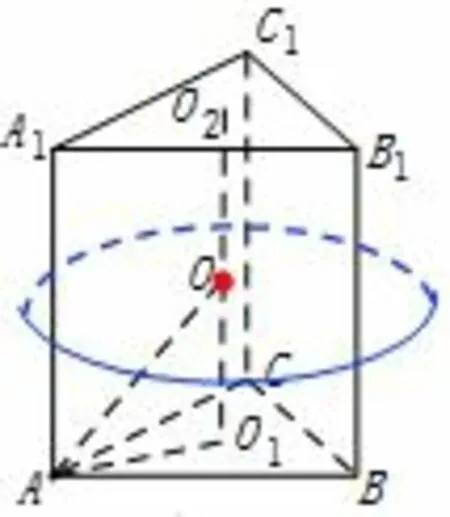
图3

根据球的两个性质可知非直棱柱无外接球,因为过上下底面外接圆圆心的垂线,相互平行,无交点(如图4),所以没有任何一点(球心)到上下各顶点的距离相等,所以斜棱柱无外接球.同理上下底面外接圆圆心连线不垂直于上下底面的棱台也没有外接球.

由线与面的交点确定球心的方法可知,如果棱锥的外接球能转化为直棱柱的外接球问题,则可直接利用上面的公式求解出外接球的半径.其主要的应用有下面两种模型:

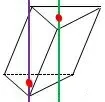
图4

应用一:有一条侧棱与底面垂直的棱锥

例3三棱锥A−BCD(图5)中,AB⊥平面BCD,CD⊥BD,且BD=2AB=2DC=2,求三棱锥A−BCD外接球的半径.

分析由于AB⊥平面BCD,因此在三棱锥的基础上可构造一个三棱柱,使之有相同的外接球,即可用上面的公式求解,其外接球半径

图5

此类模型的特点是:当棱锥有一条侧棱垂直于底面时,都可以把该棱锥还原到直棱柱中,利用R=求得其外接球半径,其中r为底面的外接圆半径,h为该侧棱的长度.

应用二:对棱相等的三棱锥

有些三棱锥虽然没有侧棱和底面垂直,但是三组对棱长度分别相等,仍然可以把它放到柱体(长方体)中进行求解.

例4求棱长为a的正四面体A—BCD的外接球的半径.

分析三棱锥中,所有棱长都相等,可以还原到正方体中,四面体的棱长是正方体的面对角线,长为a,所以正方体的棱长为即可求出外接球半径

变式1三棱锥A—BCD(图6)中,AC=BD=6,其余棱长均为5,求三棱锥A—BCD的外接球的半径.

分析三棱锥可以还原到正四棱柱中,可以得到上下面的正方形对线长为6,四个侧面的对角线分别为5,从而底面边长为高为所以正四棱柱的体对角线的一半为即三棱锥外接球半径为

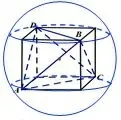
图6

变式2三棱锥A—BCD中AC=BD=5,BC=AD=6,AB=CD=7,求三棱锥A—BCD外接球的半径.

分析可以还原到长方体中,可以得到上下底面长方形的对角线长为5,左右长方形的对角线的长为6,前后面的长方形的对角线的长为7,通过解方程组求出长宽高,利用公式即可求出外接球半径

此类模型的三棱锥的特点是:三组对棱长度分别相等.当这三组对棱长度都相等时,可以放到正方体中求解;当这三组长度有两组相等时,可以放在正四棱柱中求解;当这三组长度都不等时,可以放在长方体中求解.

(三)利用线线交点确定球心

由球的性质1:过截面圆心且垂直于截面的直线过球心,可知过多面体两个不平行平面外接圆圆心的垂线的交点为球心,即线线交点确定球心.

例5在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B−AC−D(如图7),求四面体ABCD的外接球的半径.

分析如图7,直角三角形ABC与直角三角形ACD的外接圆的圆心均为斜边中点O,所以过O点作两平面的垂线,其交点是点O,所以O是外接球的球心,AC=2R=5,R=2.5.

图7

若例5中沿AC将矩形ABCD折成一个二面角B−AC−D,其平面角大小为θ(0<θ<π),则四面体ABCD的外接球半径显然是没有改变的.本题可以推广为一个重要结论:三棱锥由有公共斜边的直角三角形构成的,这个公共斜边是球的直径.

例6三棱锥的A−BCD中,三角形ABD与三角形CBD为等边三角形,BD=2,二面角A−BD−C的平面角大小为60◦,(如图8)求三棱锥A−BCD外接球半径.

图8

分析三棱锥A−BCD(图9)的球心在过底面正三角形BCD的中心O1的垂线l1上,球心又在过正三角形ABD的中心O2的垂线l2上,两直线的交点O为外接球球心.BD的中点E,OD为球的半径R,所以EO1=EO2=OE=所以R=

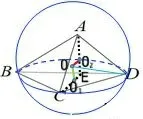
图9

此类模型的特点是:几何体中可求出两个面的二面角大小以及公共棱长度,两个面的外接圆半径,(线线交点确定球心的方法).如图9,如果二面角A−BD−C的平面角大小为θ,△CBD和△ABD外接圆半径分别为r1,r2,设BD=2a,则由余弦定理求出O1O2的长度,再由EO1OO2四点共圆,OE为外接圆直径,正弦定理得

(四)利用高线、方程确定球心

在正棱锥与旋转体中,由球的性质1:过底面圆心且垂直于截面的直线(高线)过球心及顶点,再构建直角三角形,利用勾股定理建立方程求解并确定球心位置.

例7正三棱锥S−ABC的底面边长为6,侧棱长为5,求该正三棱锥外接球的半径.

分析如图10,△ABC的外心是O1,SO1⊥面ABC,则球心在直线SO1上.

解设外接球半径为R,O1为面ABC的中心,则SO1是正四面体S−ABC的高,且外接球的球心O在SO1上,因AB=6,所以又因SA=5,所以则在三角形AOO1中,由勾股定理得解得

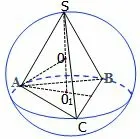
图10

此类模型的特点是:过底面外接圆圆心且垂直于底面的直线(高线)过正棱锥的顶点与球心,利用圆心与球心及底面的一个顶点构成一个直角三角形,用勾股定理解出半径.同理,圆台(棱台)的外接球球心的位置在过上下底面外心的连线(高线)上,再利用球心到上下顶点的距离相等,建立两个方程,用方程的思想求出半径,从而求解.因此可以用上面的方法求出旋转体的外接球半径计算公式: