例谈椭圆直径性质的精彩应用*
2019-04-13北京市第十二中学高中部100071
北京市第十二中学高中部(100071) 刘 刚
我们知道,圆通过伸缩变换可以得到椭圆,而圆具有丰富的几何性质,这其中的多数性质在椭圆中都可以进行推广.经过类比,圆的直径所对应的圆周角为直角推广到椭圆,可以得到下面的性质.
一.椭圆直径性质
性质如图1,AB是椭圆的一条直径(过中心的弦),P在椭圆C上,且直线PA,PB与坐标轴不平行,则直线PA,PB的斜率之积kPA·kPB为定值.

图1
证明设P(x0,y0),A(x1,y1),由椭圆对称性,得B(−x1,−y1).因为P,A在椭圆C上,所以


故直线PA,PB的斜率之积kPA·kPB为定值.
这条性质是在椭圆直径的基础上得出的,它从斜率的角度揭示了椭圆的本质,应用广泛,能够简化运算,下面举例说明.
二.应用
1.数量积定值
例1已知椭圆上任意一点M(除短轴端点外)与短轴两端点B1,B2的连线分别与x轴交于P,Q两点,O为椭圆的中心,求证:为定值.
证明不妨设B1(0,b),B2(0,−b),P(m,0),Q(n,0),则因为B1B2是椭圆的直径,且点M在椭圆上,所以由椭圆直径性质,得

所以mn=a2,由此得故为定值a2.
2.线段长度定值
例2(2018年北京市丰台区一模理科第19题)已知点在椭圆上,F(1,0)是椭圆的一个焦点.
(I)求椭圆C的方程;
(II)椭圆C上不与点P重合的两点D,E关于原点O对称,直线PD,PE分别交y轴于M,N两点.求证:以MN为直径的圆被直线截得的弦长是定值.
证明(I)略,椭圆C的方程为
3.线段长度最值
例3(2014年北京市延庆区一模)已知直线x−2y+2=0经过椭圆0)的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆上位于x轴上方的动点,直线AS,BS与直线l:x=4分别交于M,N两点.
(I)求椭圆C的方程;
(II)求线段MN的长度的最小值.

图2
解(I)略,椭圆C的方程为.
(II)如图2,由已知,得A(−2,0),B(2,0),设M(4,m),N(4,n),则因为AB是椭圆C的直径,且点S在椭圆C上,所以由椭圆直径性质,得即mn=−3,由此得当且仅当即时取等号,故线段MN的长度的最小值为
4.轨迹问题
例4(2014年全国高中数学联赛山西预赛)如图3,A、B是椭圆的长轴端点,P是椭圆上异于A、B的点,自A、B分别作l1⊥PA,l2⊥PB,l1、l2相交于点M.当动点P在椭圆上移动时,求点M的轨迹方程.
解由已知得A(−a,0),B(a,0),设M(x,y),则kAM=因为l1⊥PA,l2⊥PB,所以因为AB是椭圆的直径,且点P在椭圆上,所以由椭圆直径性质,得kPA·kPB=整理得所以点M的轨迹方程是

图3
5.位置判断
例5(2018年北京市海淀区二模文科)已知椭圆C:x2+2y2=2的左、右顶点分别为A1,A2.
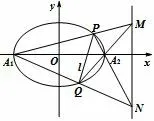
图4
(I)求椭圆C的长轴长与离心率;
(II)若不垂直于x轴的直线l与椭圆C相交于P,Q两点,直线A1P与A2Q交于点M,直线A1Q与A2P交于点N.求证:直线MN垂直于x轴.
解(I)略;(II)如图4,设M(x1,y1),N(x2,y2),由已知得因为A1A2是椭圆的直径,且P在椭圆C上,所以由椭圆直径性质,得
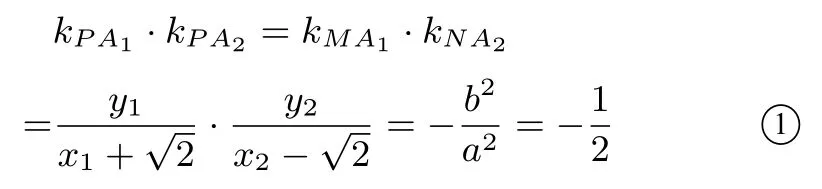
同理,

6.求离心率
例6(2014年全国高中数学联赛山东预赛)设点O为椭圆的中心,点A为椭圆上异于顶点的任意一点,过点A作长轴的垂线,垂足为M,连结AO并延长交椭圆于另一点B,连结BM并延长交椭圆于点C,问是否存在椭圆,使得BA⊥CA?
解如图5,以椭圆的中心O为坐标原点,长轴所在直线为x轴,建立平面直角坐标系,设椭圆的方程为设A(x0,y0),C(x1,y1),由已知得B(−x0,−y0),M(x0,0).因为AB是椭圆的直径,且C在椭圆上,所以由椭圆直径性质,得即

因为BA⊥CA,所以kBA·kCA=−1,即


图5
7.斜率定值
例7(2015年南京、盐城二模)如图6,在平面直角坐标系xOy中,椭圆的离心率为直线l:y=与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.
(1)求a,b的值;
(2)求证:直线MN的斜率为定值.
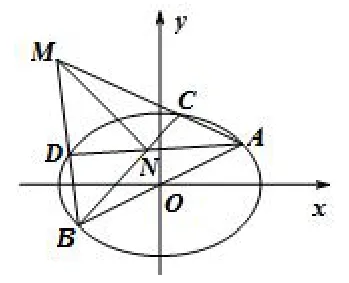
图6
证明(1)略,

化简①,得
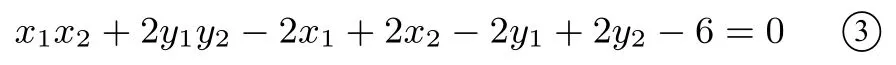
化简②,得
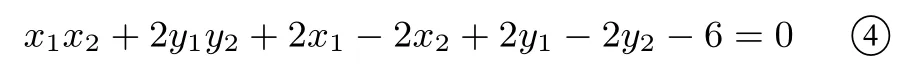
③-④,整理得x1−x2+y1−y2=0,所以故直线MN的斜率为定值−1.
8.坐标之积定值
例8(2014年南京、盐城一模)如图7,在平面直角坐标系xOy中,已知过点的椭圆C:的右焦点为F(1,0),过焦点F且与x轴不重合的直线与椭圆C交于A,B两点,点B关于坐标原点的对称点为P,直线PA,PB分别交椭圆C的右准线l于M,N两点.
(1)求椭圆C的标准方程;
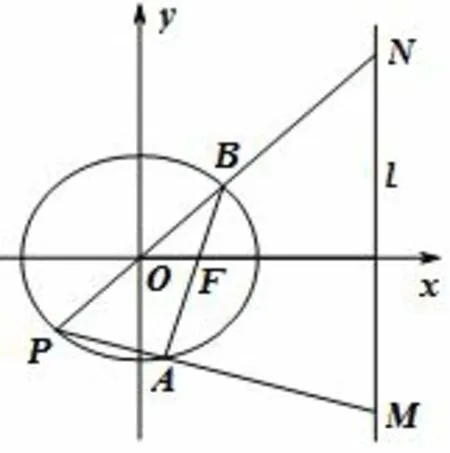
图7
(3)记M,N两点的纵坐标分别为yM,yN,试问yM·yN是否为定值?若是,请求出该定值;若不是,请说明理由.
解(1)略,椭圆C的标准方程是
(3)设B(x0,y0),则P(−x0,−y0),OB的方程为y=令x=4,得当直线AB的斜率存在时,因为PB是椭圆C的直径,且A在椭圆C上,所以由椭圆直径性质,得又kAB=所以所以直线AP的方程为令x=4,得因为点B(x0,y0)在椭圆C上,所以所以由此得yM·yN=当直线AB的斜率不存在时,易得yM·yN=−9,综上yM·yN为定值−9.
以上介绍了椭圆直径的一个性质及应用,在利用该性质解题时,要先根据题目已知条件设出相关点的坐标,然后表示出相应直线的斜率,在此基础上再借助椭圆直径的性质转化为坐标运算,从而使解题目标更加明确、有针对性,避免了联立法所带来的繁琐运算.在教学中,教师要引导学生多总结规律,适时应用,从而提高学习效率.
