钢空腹夹层板剪力键节点的极限载荷研究分析

王玉春，马克俭

(贵州大学 空间结构研究中心，贵州 贵阳 550003 )

钢空腹夹层板楼盖结构是在钢筋砼空腹夹层板的基本原理下发展而来的新型楼盖结构，与常规楼盖相比具有刚度大，跨越能力强，结构高度小，自重轻等优点。钢空腹夹层板楼盖结构[1]中钢空腹夹层板主要有T型钢构成的上下肋，方钢管和砼板共同组成，网格尺寸一般在a=1.5 m～2 m,且不少于5格。剪力键是由方钢管制成，作为一个关键节点，连接上下肋与砼板，形成了一个整体。文献[1]-[3]从理论角度得出空腹夹层板的静力计算相关方法；文献[4-7]主要集中对空腹夹层板动、静力学整体性能的分析研究。文献[8]在2 m×2 m的钢筋混凝土空腹夹层板上采用上表面中心点处施加集中荷载的加载方案，得出破坏荷载为45 T，破坏形式为弯曲破坏、延性好、安全度大、整体性能好；文献[9]从试验的角度得出设置加劲板改善了剪力键的下肋与刚肋连接区域，使应力分布更合理，以及剪力键刚度的大小能够改变砼板的受力状态，对砼板的承载力有影响;两者都没有研究参数化下的剪力键对其破坏荷载或者砼板的具体影响。文献[10]利用有限元软件模拟单向受力情况下剪力键节点域的数值模型，得出加劲板宽度在特定路径下对应力和位移的影响最大。上述研究中均没有涉及剪力键节点的极限载荷方面的研究，本文提出采用两倍斜率法研究双向受力情况下的剪力键节点的极限载荷，重点研究在不同宽度下的加劲板对剪力键节点极限载荷的影响和不同刚度下的剪力键对极限载荷的具体影响。

1 剪力键节点域特点和数值模型

1.1 构造及受力特点

剪力键节点域构造如图1所示，中间方钢管为剪力键，其内部上下两端分别设置与上下肋翼缘平齐的上肋内隔板、下肋内隔板。为了保证上下肋翼缘水平荷载的传递，方钢管的内壁与内隔板之间采用焊接。方钢管外侧四根对称轴上设置加劲板，并与上下肋焊接。实际工程中方钢管端部各焊接一块盖板，确保节点域传力的可靠。

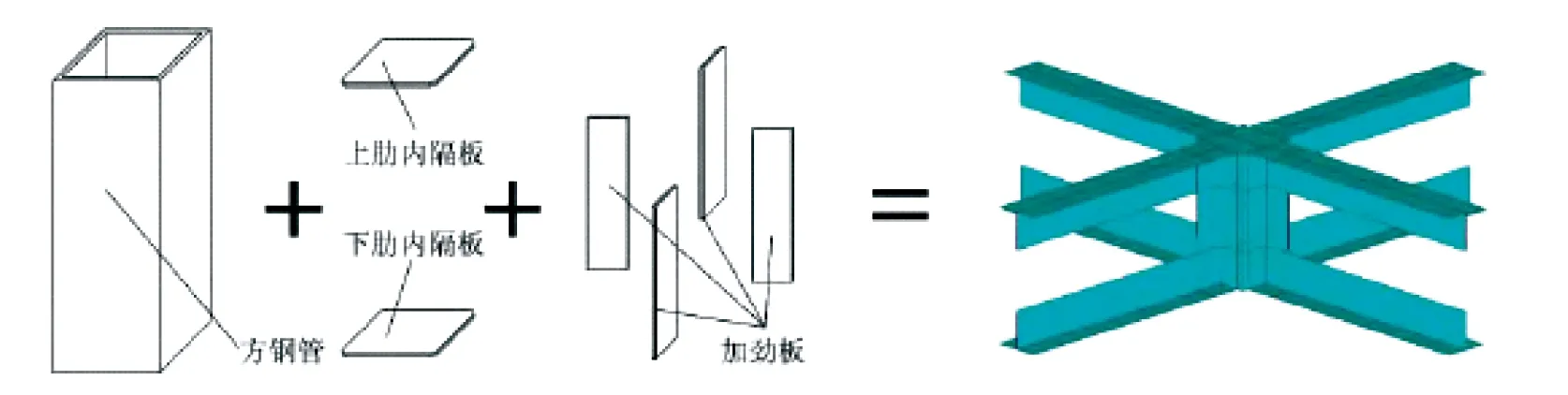
图1 剪力键节点域构造示意图Fig.1 Typical stress diagram of the square steel-tube shear connector joint

根据文献[11,12]可知，正交正放以及正交斜放的空腹夹层板楼盖的剪力键，在同一方向的上肋承受不均匀压力，下肋承受不均匀拉力。由节点平衡条件可知，上下肋的压拉差值是剪力键的剪力来源，并会产生弯矩，但是弯矩对剪力键的影响较小。这是因为剪力键的高宽比较小，截面抗弯刚度大。在空腹夹层板楼盖中剪力键根据受力特征分为三类：与上肋相连局部受压大；与下肋相连的局部受拉大；与上下肋相连受力差别不大。

1.2 数值模型边界条件

根据剪力键节点域的受力特点，上下肋在跨中反弯点处截断，使用ANSYS通用有限元分析软件建立数值模型。取消盖板的设置，有限元简化模型最终如图2所示。以剪力键方钢管中心为坐标原点建立三维坐标，下肋分别为±X、±Y轴，Z轴指向上肋内隔板。根据不同位置的受力特征，选取双向受力情况下剪力键节点域，最终采用在反弯点处的下肋X轴、Y轴直接加载，上肋X轴、Y轴采用固定铰支座约束，上下肋-X轴、-Y轴采用滑移支座约束。即下肋X轴、Y轴的反弯点处沿X正向施加水平荷载(如表1所示)，忽略形体的单向平面简图如图3所示。

a)未设置加劲板区域 b)设置加劲板区域图2 数值模型示意图Fig.2 Numerical models of the joint

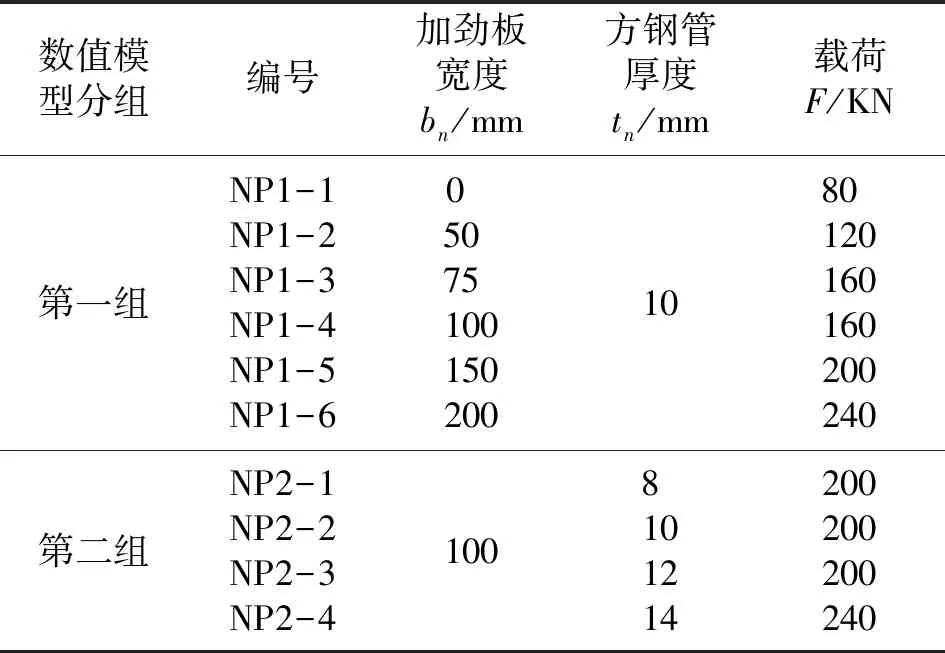
数值模型分组编号加劲板宽度bn/mm方钢管厚度tn/mm载荷F/KN第一组NP1-1NP1-2NP1-3NP1-4NP1-5NP1-6050751001502001080120160160200240第二组NP2-1NP2-2NP2-3NP2-41008101214200200200240

1.3 数值模型的参数

本文采用文献[13，14]介绍的数值模拟方法。数值模型构件中采用shell181单元，钢材为ASTM1020，钢材实际应力-应变曲线采用文献[15]中曲线(见图4)，弹性模量Es=2.1×105N·mm-2，泊松比ν=0.3，屈服应力fy=365 N·mm-2。采用 Mises屈服准则，并且认为材料是非线性等向强化。方管尺寸采用工程尺寸200 mm×200 mm(厚度如表1所示)，高度450 mm,内隔板尺寸200 mm×200 mm×10 mm，上下肋T形截面尺寸150 mm×150 mm×10 mm,加劲板厚度10 mm。

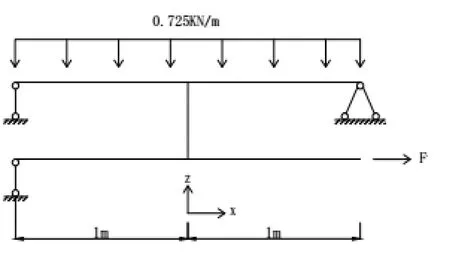
图3 平面简图Fig.3 Plane diagram

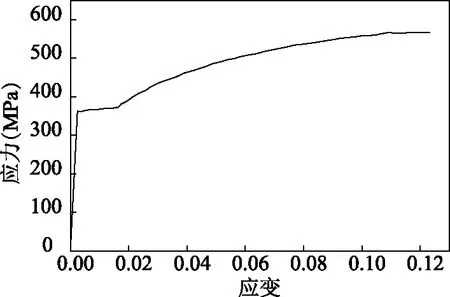
图4 应力-应变曲线Fig.4 True stress-strain curve of ASTM 1020

2 数值模型计算结果及分析

逐级施加荷载作用在剪力键节点域，寻找该节点域最初出现的最大等效应力对应节点，研究发现该节点位于剪力键(或加劲板)与上下肋交界处附近。研究此节点在逐级荷载作用下对应的应变关系，该应变为弹性应变和塑性应变之和。本文采用两倍斜率法作为极限载荷的判断依据，经ANSYS运算，依次得出表1对应模型下的极限载荷。

2.1 不同宽度下的加劲板对剪力键的极限载荷的影响

表1所示第一组相应的结果如图5所示：载荷-应变曲线弹性阶段的拟合直线方程为y=ax+b，两倍斜率下的直线方程为y=0.5ax+b。该直线与载荷-应变曲线交点对应的载荷即为极限载荷。极限载荷与加劲板宽度相关，随着加劲板宽度的增加，不仅弹性阶段的承载力增大，而且弹塑性阶段剪力键的极限载荷Fn也增大(见表2所示)。这是因为设置加劲板能够显著增强方钢管平面外受力性能，增大剪力键的整体性能，从而提高了极限载荷。但是极限载荷增加量与加劲板宽度之比先增大后减小，剪力键的加劲板宽度等于100 mm时达到最大值860.30 KN/m。载荷-应变曲线在略小于应变0.002对应弹性阶段的最大载荷，而应变在0.002时对应钢材的屈服强度，剪力键在弹性阶段的变形遵循材料的特性。极限载荷对应的弹塑性应变略小于0.007。

表2 加劲板宽度对极限载荷的影响

图5 不同宽度下加劲板的极限载荷Fig.5 Ultimate load of stiffening plate at different widths

2.2 不同刚度下的加劲板对剪力键的极限载荷的影响

选取典型剪力键作为代表，表1所示第二组相应的结果如图6所示：极限载荷与刚度(方钢管厚度)相关，随着方钢管厚度的增加，不仅弹性阶段的承载力增大，而且弹塑性阶段剪力键的极限载荷Fn(见表3所示)也增大，这是因为方钢管厚度增大，提高了剪力键的整体刚度。同时极限载荷与方钢管厚度比值也随之增大(见表3所示)，但厚度从10 mm到14 mm的比值增加幅度并没有太明显。载荷-应变曲线在略小于应变0.002对应弹性阶段的最大载荷，而应变在0.002时对应钢材的屈服强度，剪力键在弹性阶段的变形遵循材料的特性。极限载荷对应的弹塑性应变略小于0.007。

表3加劲板厚度对极限载荷的影响

Tab.3Effectofstiffeningplatethicknessonultimateload

编号NP2-1NP2-2NP2-3NP2-4tn/mm8101214Fn/KN119.01154.14185.31216.73Fn/tn/(KN/m)14.88 15.41 15.44 15.48

图6 不同厚度下的极限载荷Fig.6 Ultimate loads at different thickness

3 结论与建议

多组剪力键节点域数值模型经有限元软件计算分析中可得出以下结论与建议：

(1)剪力键节点域的极限载荷与加劲板有关，虽然加劲板宽度的增加有利于极限载荷的增大，但是在工程实际中剪力键高度为450 mm时，我们考虑结构与材料最优解时可设置加劲板宽度为100 mm左右。

(2)剪力键节点域的极限载荷还与刚度有关，刚度增大有利于提高极限载荷。设计中在满足结构要求时尽量选择适宜厚度的钢材，例如在剪力键高度为450 mm时满足极限载荷的条件下，优先选择方钢管厚度10 mm或者12 mm,从而节约材料，提高经济化效益。

(3)设计中为了提高极限载荷我们要综合考虑加劲板和刚度，但是极限载荷与加劲板、刚度、剪力键高度具体关系需要进一步研究，为实际工程提供可靠依据。