空腹桁架梁-空腹夹层板楼盖的静力性能分析

2019-04-12苏铜军肖建春马克俭袁增嵘

贵州大学学报(自然科学版) 2019年1期

苏铜军，肖建春，马克俭，袁增嵘

(贵州大学空间结构研究中心，贵州贵阳 550000)

随着大跨度建筑的兴起，人们不断追求具有高性能和低能耗的新型结构。马克俭[1]教授首次提出了“钢筋混凝土空腹夹层板楼盖结构”这一新型空间网格结构，保留空腹网架优点而又克服其抗剪刚度差的缺点。通过实践应用推广[2]，新型空腹夹层板及其组合结构相继出现。2017年，关于昆明滇池国际主体结构会展中心跨环湖平台方案选择上，马克俭教授进一步创新，提出了空腹桁架梁-空腹夹层板新型结构。宋赟[3]和才琪[4]分别对窝型钢网格盒式结构和蜂窝形钢空腹夹层板楼盖做了一定的研究。冯献慧[5]对正交斜放空腹夹层板楼盖自振特性进行了分析。文献[6]～[8]对空腹夹层板的结构基本力学性能等做了基础性理论研究。文献[9]～[14]对空腹夹层板静力性能做了不同的分析。由于空腹桁架梁-空腹夹层板结构提出时间不长，为了进行初步分析，采用有限元法对结构挠度进行参数化分析。

1 建立有限元模型

利用大型有限元软件采用数值模拟的方式建立空腹桁架梁-空腹夹层板有限元模型。有限元模型平面尺寸为48 m×27 m，网格采用正交正放的形式，网格大小为3 m×3 m，空腹夹层板厚度为1.6 m(其中混凝土板厚80 mm)，两层空腹夹层板之间的净高度为5.4 m。如图1所示，为空腹桁架梁-空腹夹层板半跨平面布置图。如图2所示，为空腹桁架梁-空腹夹层板的48 m边立面图。

图1 结构平面布置图Fig.1 Structural plan layout

图2 空腹桁架梁-空腹夹层板立面图Fig.2 Vertical diagram of vierendeel truss beam-vierendeel sandwich plate

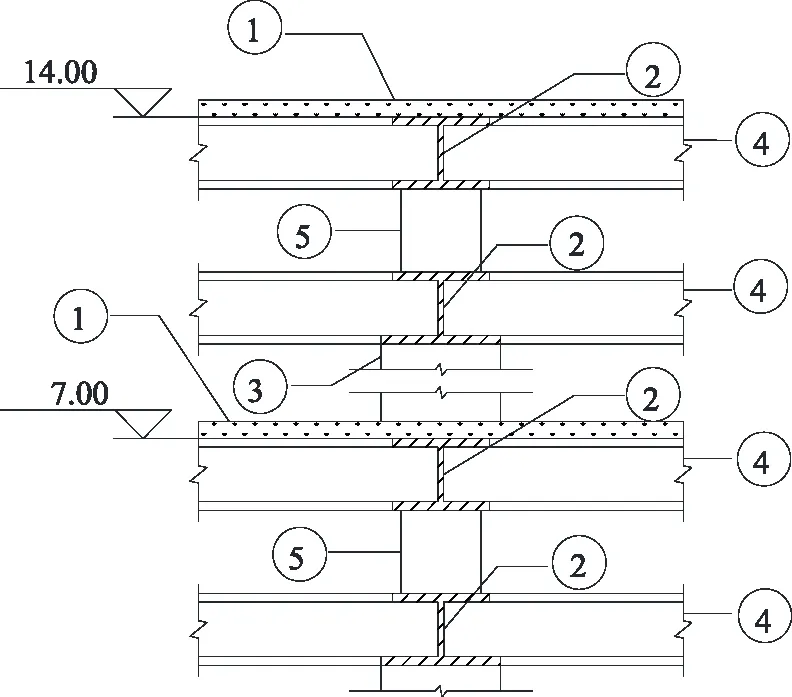
图3 A-A剖面图Fig.3 A-A Section view

图4 有限元模型Fig.4 Finite element model

图3为A-A的剖面图，其中1为80 mm厚的钢筋混凝土楼盖，2为空腹桁架梁上、下弦空腹弦杆，3为空腹桁架梁的双肢格构柱，4为正交正放钢空腹夹层板上、下弦杆，5为圆钢管剪力键。钢筋混凝土楼板与空腹夹层板上弦H型钢通过栓钉连接，形成具有整体工作特性的组合楼盖。

如图4，结构分为两层，两层楼面空腹夹层板上下肋和双肢格构柱组成空腹桁架梁。楼面结构恒荷载与活荷载组合荷载取4.5 kN/m2,在ANSYS有限元软件中，通过定义加速度的方法定义自重系数为1.0，即将自重全部换算成相等的荷载[5]。27 m边每隔9 m设置一根方钢管柱，两边各设置4根柱，呈对称布置，柱底固定，整个结构荷载由这8根柱承受。

为了分析空腹桁架梁-空腹夹层板挠度变形影响的因素，建立有限元模型分别考虑表层混凝土板厚、空腹桁架梁上下肋和空腹夹层板上下肋刚度、剪力键刚度、方钢管柱刚度和跨高比对空腹桁架梁-空腹夹层板楼盖挠度变形的影响。由于模型比较大，计算资源有限，有限元模型采用BEAM188单元模拟空腹桁架梁-空腹夹层板中的梁单元，SHELL181模拟混凝土楼板单元。有限元各构件的尺寸和参数如表1所示。

表1 有限元模型结构构件尺寸和参数

2 位移分析

楼盖上静力采用均布荷载q，在q作用下，楼板跨中挠度可用下式计算：

式中w为楼板的跨中挠度，Cs为挠度系数，与楼板边界条件有关；L为楼板的跨度；E为弹性模量，h为楼盖高度，ν为泊松比。由上式可知，楼板挠度与竖向刚度呈反比例关系。通过研究空腹桁架梁-空腹夹层板在均布荷载作用下的最大挠度来分析结构的竖向刚度[15]。

在组合荷载作用下，空腹桁架梁-空腹夹层板的位移分布云图(单位：mm)和mises应力云图(单位：Mpa)分别如图5和图6。由图5可知，空腹桁架梁-空腹夹层板有柱的两边位移非常小，中部位移在竖向荷载作用下由两边向中间逐渐增大。由于空腹夹层板只在两边布置方钢管柱，结构明显呈单向板弯曲变形，变形后整体呈椭圆弧分布，表明空腹桁架梁-空腹夹层板结构质量分布均匀，各构件协同工作性好，整体稳定性好。空腹桁架梁-空腹夹层板的跨度为48 m，由图5可以看出，楼板最大挠度为105.3 mm，为楼盖跨度的1/456，满足《混凝土结构设计规范》(GB50010-2010)对大跨度楼盖挠度限制1/300的要求。

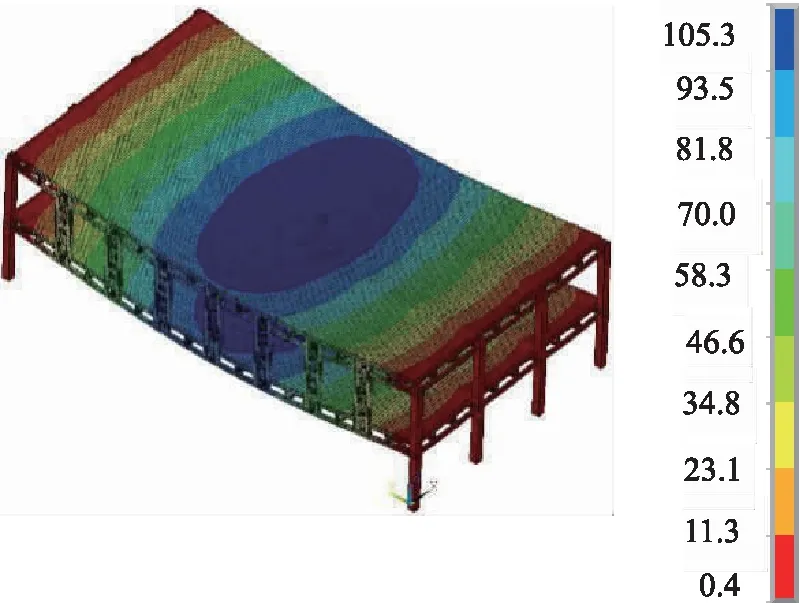
图5 空腹桁架梁-空腹夹层板位移分布云图Fig.5 Cloud diagram of displacement distribution of vierendeel truss beam-fasting sandwich plate

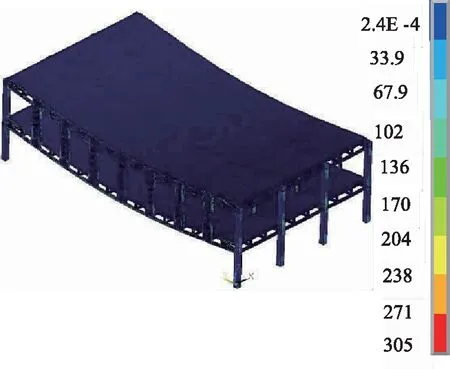
图6 空腹桁架梁-空腹夹层板mises应力分布Fig.6 Mises stress distribution of vierendeel truss beam-vierendeel sandwich plate

图6可以看出，结构最大mises应力为305 MPa，Q345钢屈服应力为310 Mpa，整个结构最大应力未达到屈服应力。mises应力也是对称分布，整个楼板应力分布非常均匀，节点处应力相对较大，符合空腹夹层板的受力特性。

3 楼盖挠度的参数化分析

结构挠度的大小直接影响建筑使用的安全性及人们对建筑的感官印象，为了分析影响空腹桁架梁-空腹夹层板楼盖挠度的影响因素，建立94个有限元模型，分别考虑表层混凝土楼板厚度、空腹桁架梁上下肋、剪力键刚度、边柱刚度和跨高比等因素对空腹桁架梁-空腹夹层板在正常使用荷载作用下挠度的影响。

3.1 表层混凝土板厚度对楼盖挠度的影响

空腹网架在设计时不考虑表层混凝土对楼盖竖向刚度的影响，而空腹夹层板需要考虑，这充分利用混凝土板对楼盖竖向刚度的贡献。而楼盖竖向刚度主要通过楼盖挠度来体现的。有限元建模时是采用面荷载直接施加在表层混凝土板上的，为了研究表层混凝土板厚度对楼盖挠度的影响，根据表层混凝土楼盖设计标准，建立15组楼度厚度不同的有限元模型，表层混凝土楼板厚度分别为20～160 mm，以10 mm的梯度递减。混凝土板厚度与最大挠度曲线关系如图7所示，h表示混凝土板厚度，w表示楼盖最大挠度。

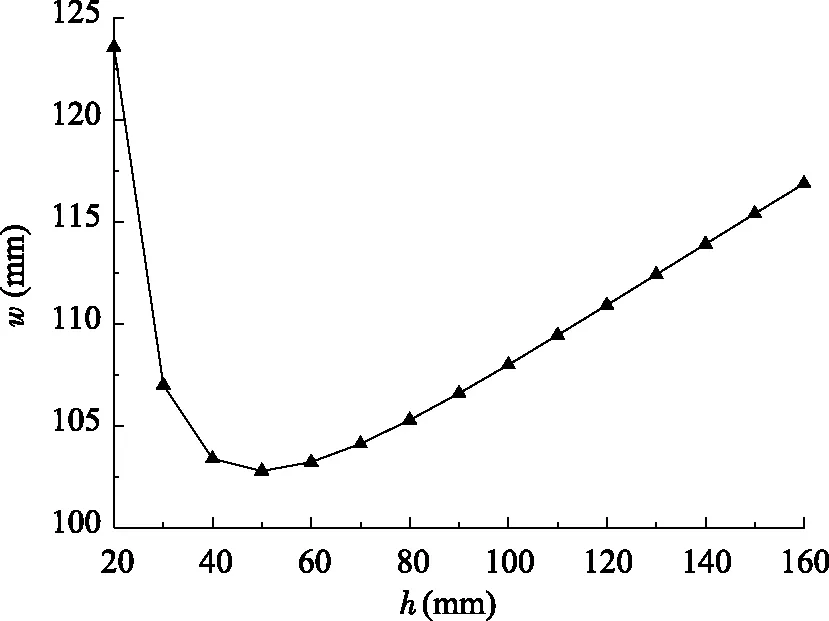
图7 混凝土板厚度对楼盖挠度影响曲线图Fig.7 Curves of effect of concrete slab thickness on floor deflection

由图7可知，随着混凝土板厚度的增加，空腹桁架梁-空腹夹层板楼盖跨中最大挠度先逐渐减小，当板厚大于50 mm时挠度越来越大。混凝土板厚度由20 mm增加到50 mm时，楼盖最大挠度由123.6 mm减小到102.8 mm，减小幅度为20.2%。这主要是因为随着板厚的增加，混凝土板对结构竖向刚度的贡献值大于其对楼盖自重的影响，板厚增加对楼盖竖向刚度的增加是有利的,并且板厚对楼盖最大挠度的影响程度也逐渐降低。混凝土板厚度由50 mm增加到160 mm时，楼盖最大挠度由102.8 mm增加到116.9 mm，增加幅度为13.7%。这主要是因为当混凝土板厚达到一定厚度时，混凝土板对结构竖向刚度的贡献值小于其对楼盖自重的影响，这时板厚增加对楼盖竖向刚度的增加是不利的，并且随着混凝土板厚度的增加，其对楼盖最大挠度的影响程度也逐渐增加。实际工程中，混凝土板要具有一定的刚度和强度在受力时才能保持应力、挠度均匀分布，一般情况下混凝土板厚取60～160 mm，在这一范围楼盖挠度改变值为13.2%。

3.2 上肋和下肋刚度对楼盖挠度的影响

空腹桁架梁-空腹夹层板的挠度以空腹桁架梁的上肋和下肋起主导作用，非空腹桁架梁的空腹夹层板的上肋和下肋次之。空腹桁架梁类似于空腹夹层板中的主梁，由空腹上弦、空腹下弦及格构柱组成。空腹桁架梁的上肋和下肋是空腹上、下弦的主要构件，是将楼面主要荷载及自重传递到竖向结构的主要传力构件。为了保证空腹桁架梁的上肋和下肋具有足够的刚度，采用H型钢，空腹上弦和空腹下弦的上、下肋截面尺寸见表1。为了研究空腹桁架梁上肋和下肋的刚度对空腹桁架梁-空腹夹层板挠度的影响，通过改变尺寸来改变上、下肋刚度，建立20个不同模型，分别研究上、下肋的梁的高度、宽度、腹板厚度和翼缘厚度对空腹桁架梁-空腹夹层板挠度的影响。建立模型时，保证空腹上弦和空腹下弦的上、下肋的截面尺寸都一致。

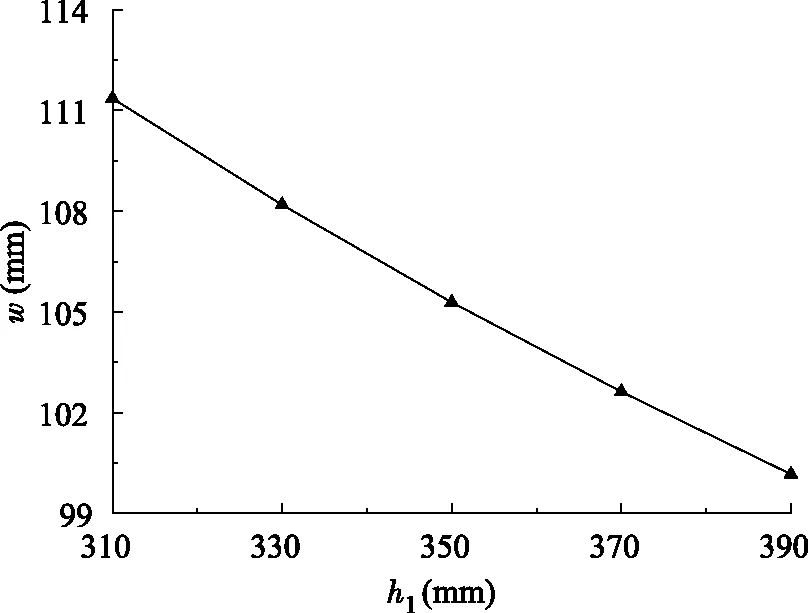
图8 梁高与挠度的关系Fig.8 Beam height and deflection

图9 梁宽与挠度的关系Fig.9 Relationship between beam width and deflection

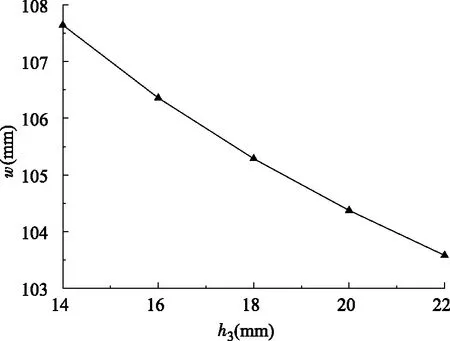
图10 腹板厚度与挠度的关系Fig.10 Relationship between web thickness and deflection

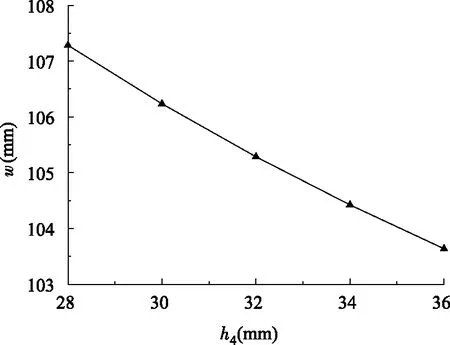
图11 翼缘厚度与挠度的关系Fig.11 Relationship between flange thickness and deflection

由图8～11可以看出，空腹夹层板的挠度随着梁高、梁宽、腹板厚度和翼缘厚度的增大而逐渐减小，其中梁高、梁宽与挠度关系几乎呈直线变化，腹板、翼缘随着厚度的增加对挠度的影响越来越小。图8中梁高从310 mm到390 mm变化对挠度的影响达达到11.2%，梁宽从310 mm到390 mm变化对挠度的影响占到3.9%，腹板厚度从14 m到22 mm变化对挠度的影响为3.9%，翼缘厚度从28 mm到36 mm变化对挠度的影响达到3.6%。可以得出，空腹桁架梁上下肋的梁的高度对楼盖挠度起主要作用，梁高增加的时候空腹夹层板的厚度也在增加，梁的宽度、腹板厚度、翼缘厚度对挠度影响基本相似，影响不是很大。

非空腹桁架梁的空腹夹层板的上下肋的梁，梁高从260 mm增加到340 mm，挠度从106.3 mm降到104.3 mm，挠度改变率为1.9%；梁宽从210 mm增加到290 mm挠度从105.8 mm降到104.9 mm，挠度变化率为0.86%；梁腹板厚度从4 mm增加到12 mm挠度从105.9 mm降到105.0 mm，挠度变化率为0.86%；翼缘厚度从12 mm增加到20 mm挠度从106.0 mm降到104.9 mm，挠度变化率为1.0%。非空腹桁架梁的空腹夹层板的上下肋的梁对挠度的变化与空腹桁架梁类似，但是对挠度的影响程度要小很多。由此可以知道，空腹桁架梁上下肋的梁是影响空腹桁架梁-空腹夹层板挠度的主要因素之一。

3.3 剪力键刚度对楼盖挠度的影响

剪力键被称之为“超短柱”，是连接上肋和下肋的重要构件，承担着板内横向剪力的作用[16]。空腹夹层板的剪力键的高度是由空腹夹层板的高度与上肋和下肋的高度决定的。剪力键采用圆形钢管，可以通过改变圆钢管剪力键的壁厚和管径两种方法来改变剪力键的刚度。在建立模型时，采用改变剪力键壁厚的方法，保证圆钢管外径为400 mm不变，通过改变内径尺寸来改变壁厚。选取7个有限元模型进行分析，剪力键的厚度分别为14～38 mm，以4 mm的梯度递增。如图12所示，剪力键厚度对楼盖挠度影响曲线图，图中t1为剪力键厚度。采用改变剪力键管径的方法，保证管壁厚度为26 mm不变，改变外径和内径尺寸。选取7个有限元模型进行分析，剪力键外径分别为280～520 mm，以40 mm的梯度递增。如图13为剪力键管径对楼盖挠度的影响曲线图，t2为剪力键管径。

由图12可知，结构挠度随着剪力键壁厚的增加而逐渐减小，挠度曲线大致为非线性关系，剪力键壁厚从14 mm增加到38 mm，挠度由109.8 mm降到104.03 mm，挠度下降了5.5%。并且随着剪力键壁厚的增加，其壁厚对结构挠度的影响越来越小。主要是因为剪力键将上肋和下肋链接为一个整体，当剪力键厚度过小时，不能提供足够大的抗剪刚度，使整体结构竖向刚度较低，因此挠度随剪力键壁厚的增大而减小。但是当剪力键具有足够的抗剪能力时，再增加剪力键壁厚会使结构自重增加，从而使剪力键对结构挠度影响程度减弱。

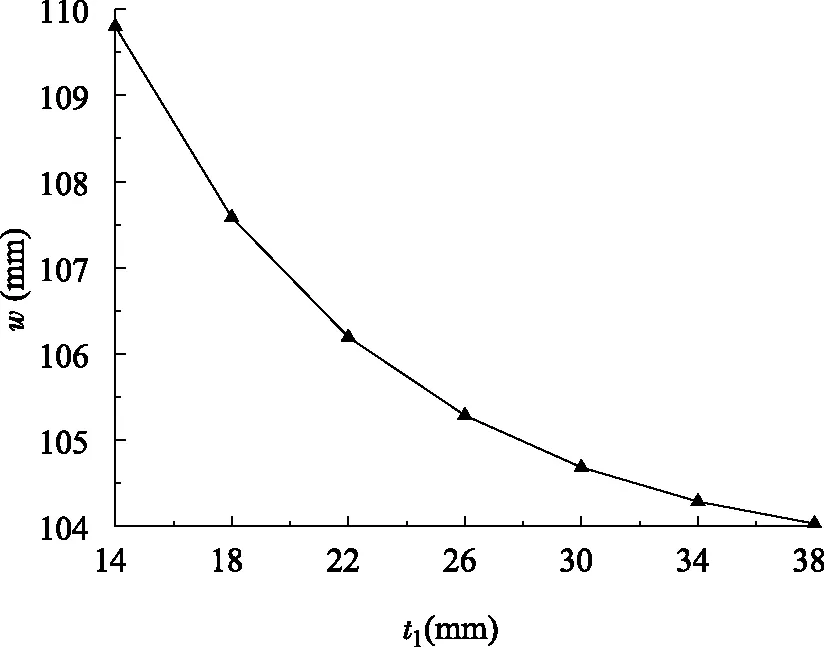
图12 剪力键壁厚对楼盖挠度影响曲线图Fig.12 The effect of wall thickness of shear keys on the deflection of floor

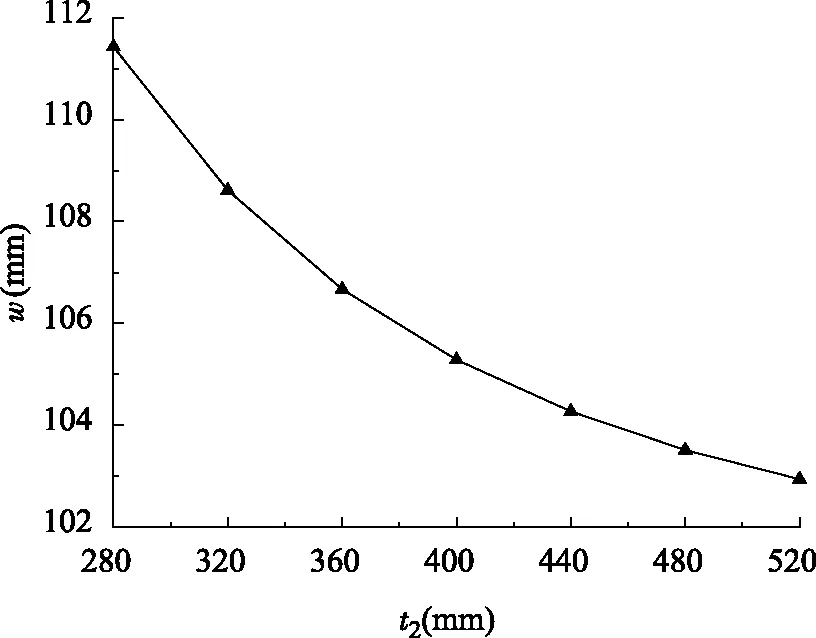
图13 剪力键管径对楼盖挠度影响曲线图Fig.13 Curve diagram of effect of shear key pipe diameter on floor deflection

由图13可知，保持剪力键壁厚不变，随着剪力键管径增加，结构挠度逐渐减小，剪力键管径从280 mm增加到520 mm，结构挠度从111.4 mm降到102.9 mm，挠度下降了8.3%。结构挠度变化趋势与图12类似，剪力键管径越大，其对结构挠度的影响程度越小。也是由于剪力键抗剪刚度的能力决定的，因此，在实际工程中需要重点验算剪力键的抗剪强度。[17]

3.4 方钢管柱对楼盖挠度的影响

整个结构平面尺寸布置为48 m×27 m，其中48 m边不设柱子，27 m边每隔9 m设1根方钢管柱，一共设8根柱，结构的所有荷载及自重均由这8根方钢管柱承载。方钢管柱与剪力键很类似，其刚度对楼盖跨中挠度也有一定的影响。与研究剪力键一样，通过控制柱壁厚改变柱宽度和控制柱宽度改变壁厚来研究方钢管柱刚度对结构挠度的影响。每一种研究方法分别选取7个有限元模型进行分析。图14是保持柱壁厚不变改变柱宽度得到的结构挠度曲线图，柱宽度为650～950 mm，以50 mm梯度逐渐增加,n1为方钢管柱宽度。图15是保持柱宽度不变改变柱壁厚得到的结构挠度曲线图。柱壁厚为46～70 mm，以4 mm梯度逐渐增加，n2为方钢管柱壁厚。

图14 方钢管柱宽度对楼盖挠度的影响曲线图Fig.14 The influence of the width of square steel tube column on the deflection of floor

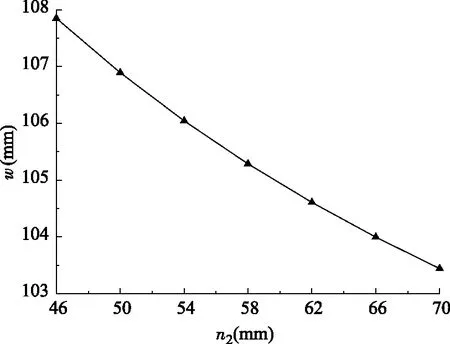
图15 方钢管柱壁厚对楼盖挠度的影响曲线图Fig.15 The effect of wall thickness of square steel tube column on the deflection of floor

如图14所示，方钢管柱宽度从650 mm增加到950 mm，结构挠度由112.6 mm降到100.5 mm，挠度下降了12.0%。如图15所示，方钢管柱壁厚从46 mm增加到70 mm,结构挠度由107.8 mm降到103.4 mm，挠度下降了4.3%。边柱壁厚和宽度与挠度的变化趋势与剪力键基本相似。

3.5 跨高比对楼盖挠度的影响

跨高比是指楼盖的跨度与高度的比值，在实际工程中空腹夹层板的跨高比一般采用25～35。一般楼盖结构的竖向刚度随着跨高比的增大而增大，空腹桁架梁的刚度也会不断增大。为了研究空腹桁架梁-空腹夹层板结构跨高比对结构挠度的影响，保持结构跨度不变，通过改变剪力键的高度来控制跨高比。建立11个有限元模型，跨高比为25～35，以1为梯度增大。分析结果如图16，图中λ表示楼盖的跨高比。

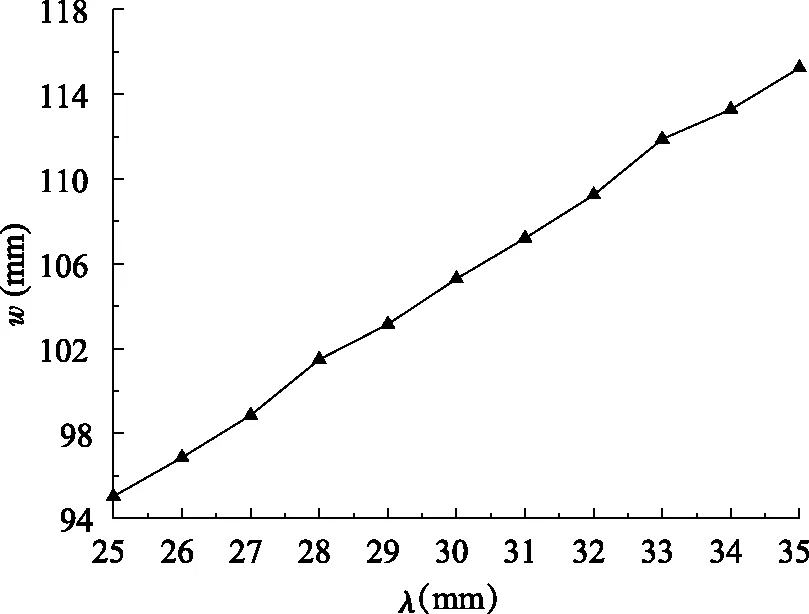
图16 跨高比与挠度的曲线位移图Fig.16 Curve displacement diagram of span height ratio and deflection

由图16可知，随着跨高比逐渐增加，空腹桁架梁-空腹夹层板的楼盖挠度也逐渐增加。跨高比从25增加到35，楼盖挠度从95.02 mm增加到115.24 mm，挠度上升了21.3%。从图中可以看出，结构跨高比在25～35范围内，其挠度与跨高比近似线性变化。这主要是因为随着跨高比的增大，空腹桁架梁-空腹夹层板三维空间受力性能逐渐减弱，导致竖向刚度不断减小。在实际工程中，如果对结构空间高度没有特别的要求，可以通过增大空腹夹层板的跨高比来降低楼盖挠度，以满足工程需要。

综上所述，在使用范围内，各主要参数对空腹桁架梁-空腹夹层板竖向跨中挠度的影响如表2所示。