一种变径减阻的方法★
2019-04-12陈永健冯仁杰程鹏月
陈永健 冯仁杰 程鹏月 刘 锦 赵 琦
(河北建筑工程学院,河北 张家口 075000)
管道内的流体,由于流体流经变径结构时会产生局部阻力损失,这是因为流动边界条件改变,而流体没有及时的改变,会产生一定的旋涡,由于旋涡的产生会造成局部阻力损失[1],本文在最小作用量原理基础上,提出了一种减小局部阻力损失的方法即通过找到流体流经减阻结构时的流线方程,改变流体的外部边界形状,使得边界形状与流体流线最大限度重合,减小流体流经变径的局部阻力损失,如何根据最小作用量原理找到流体流经变径结构的流线方程,是本文的重点。
1 最小作用量原理的一般表述
自然界中各种类型的宏观现象(例如:力学、热学、光学、电磁学等现象)[2]在一切实际现象的发生过程中,始终满足:


最小作用量原理有两个层次的应用,第一个层次就是描述物理过程基本规律的原理,即一般用变分的形式将偏微分方程形式的规律统一起来;第二个层次则是根据基本规律用来实现对实际物理过程优化设计和控制。
2 减阻方法的提出
最小作用量原理现在已经成为物理学研究方法中的最基本的方法,也是科学家研究宇宙问题时最简单明了的基本准则,更是描述客观事物规律的一种方法[3]。即认为所有的动力学体系均可以用作用量方式来描述,通过作用量取极值来确定。认为作用量最小的那个,是物体的实际运动。而在费曼路径积分方法中,认为粒子每一条路径的权重其实是这条路径的作用量所决定的,但这是量子体系的描述,不能说体系中挑选了某一条最近的路径,而是所有的路径都对动力学作了贡献。我们不用考虑是否是作用量最小,只知道在作用量取得极值时,就代表了物体实际的运动过程[4]。
最小作用量原理反映了事物的变化在运动路径上所遵循的规律。由于最小作用量原理的简单和普遍适用特性,我们在应用最小作用量原理的思想研究流体质点通过变径问题时,通过使用最小作用量方法来观察流体质点所走的路径,并找到流体质点运动的真实路径而不是其他的路径。我们不仅要考虑流体质点从A到B可能走的所有路径,而且还要考虑它走这一段路程的所有可能的形式。我们可以把在一定时间内流体质点走过这一路径的每一种特定形式定义为一个“经历”。通过定义相关作用量变化的函数,然后算出一给定流体质点在任一经历下的作用量,我们就完全掌握住了这个物体的运动情况。当我们找到变径时的作用量函数时,根据最小作用量原理可以知道,它不同于一般泛函数(简单的说,泛函的定义域是函数集,值域是数集,即泛函是从函数空间到数域的一个映射)取最值原理,我们按照费曼的解读可以知道,最小作用量原理不要求泛函数取得最大值或者最小值,甚至不需要取得极大值或极小值,仅仅取得驻值就有可能代表了真实的物理过程。也就是说当此函数取极值时,我们就可以确定流体流过变径区域的真实运动轨迹,然后通过改变固体边界保证流体流动轨迹与固体边界完全重合时,或者尽最大可能重合时,使得流体流过变径区域既没有碰击,又无因脱离而产生的附加能量损失,从而使得流体通过变径区域的阻力最小。这即是通过最小作用量原理提出减阻方法的核心思想。
在研究流体变径问题时,只需要找到作用量方程即拉格朗日函数,而无需参照特别的坐标系,这是我们通常使用牛顿定律研究力学所不具有的。它表现形式更加简单,几乎一个简洁的的公式就可以求解所有的力学量。尽管和牛顿运动定律表现形式不同,但是它们之间是等价的。
3 定义作用量函数
我们可以知道,理想不可压缩流体恒定流元流能量方程为:

我们把前两项相加,以Hp表示:
其中,Hp为元流断面测压管水面相对于基准面的高度,称为测压管水头,表明单位重量的流体具有的势能称为单位势能。
三项相加,以H表示:
其中,H为总水头,表明单位重量的流体具有的总能量,称为单位总能量。
根据元流能量方程式,我们可以知道理想不可压缩流体恒定元流中,各断面总水头相等,单位重量的总能量保持不变。元流能量方程式,确立了在一元流动中的动能和势能,也确立了流速和压强相互转换的普遍规律。在流体变径过程中我们只考虑动能和压能的相互转化关系,为此我们可以根据元流能量方程式定义作用量的表达式方程。
定义拉格朗日函数:
定义时间的函数:
l(t)=t。
作用量为:
其中,δS为S的变分,我们可以知道只要使得:
δS=0。
我们即可求解出流体从A点到B点的真实路径,即流体从A点到B点的真实路径轨迹。
4 求解拉格朗日微分方程
已知条件:
xt1=xA。
xt2=xB。
即流体每条路径都是从t1时刻从A点出发,在t2时刻到达B点,这些地点和时间都保持不变,如图1所示。

为了进一步解析方程我们可以设定几个参数:
1)流体从A点流动到B点的任意路径是x′(t),作用量是S′。
2)流体从A点到B点的真实路径x(t),作用量是S。
3)任意路径与真实路径的偏移量η(t)=x′(t)-x(t)表示任意路径与真实路径的微小差别。
在此基础上对其进行求解,只要使得在偏移量η的第一次近似上应等于0:
η(t1)=0,η(t2)=0。
我们把参数带入作用量公式可得:
那么通过真实路径对此进行表示作用量把:
x′(t)=η(t)+x(t)。
代入该作用量公式进行替换那么我们可以得到这样的一个表达式:
通过对其平方项进行展开,我们可以得到:
对于最小偏移量η的二次项忽略不计,因此动能的部分我们可以得到这样的一个表达式:

对于二阶和更高阶η,忽略不计那么S为:
我们现在的问题是虽然我们不知道x(t)是什么,但是我们知道不管η是什么,但是我们知道δS=0,这一积分为总是为0,我们只要保证δS=0,即是得到最终曲线。
通过分部积分法可得:
由于η(t1)=0,η(t2)=0。积分结果为0。
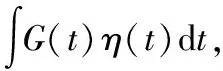
据此我们得到了在流体通过变径过程中的微分方程,只有对于满足这微分方程的路线,也就是流体通过变径时候的真实路径。然后通过初始条件我们可以求出质点的运动轨迹。
5 结语
本文在流体中应用最小作用量原理思想提出了变径减阻的方法,介绍了最小作用量原理一般表述和应用方法,最小作用量原理思想虽然和物理学中牛顿定律表现形式不同但是它们是等价的,最小作用原理比牛顿第二定律更加方便,最小作用量原理把寻找拉格朗日量作为出发点,推导出质点运动轨迹满足的微分方程,因此我们可以通过最小作用量原理推导出流体变径时流体的真实的运动轨迹,由于流体动力学研究的主要问题是流速和压强在空间的分布,本次针对流体变径中流线的分布,通过简化物理模型,不同于以往用欧拉法来研究流体的流场而是应用于用拉格朗日法来描述质点的运动找到流体变径时的真实路径。流体变径时主要是压能和动能之间的相互转化,为了应用最小作用量原理思想到找到流体变径时候的流体轨迹方程,把压能和动能转化关系定义为作用量函数然后对其进行求驻值,从而确定流动的微分方程式,通过初始条件我们可以知道流体变径时,流体真实的路径,通过对流体进行进一步的分析,确定了减阻结构的形状,这样我们为流体通过变径结构时提供了理论基础也为以后的变径结构提供了设计依据。
