基于多核多分类相关向量机的模拟电路故障诊断方法
2019-04-12高明哲许爱强唐小峰张伟
高明哲 许爱强 唐小峰 张伟
当前,模拟电路广泛应用于通信、控制、导航等电子系统中,随着对电子系统可靠性需求的不断提高,模拟电路的故障诊断技术也已成为当前电路测试领域的研究热点[1].统计数据表明,在数模混合的复杂电子系统当中,超过80%的元件故障发生在模拟电路部分[2],然而模拟电路的故障诊断技术却发展缓慢,难以达到实际应用的需求.导致这种现象的原因主要有:1)模拟电路的故障现象十分复杂,任何一个元件的参数超出容差就属故障,各类软、硬故障及多重并发故障导致了模拟电路的故障状态是无限的,故障特征可以是连续的[3−4];2)模拟电路的输入–输出关系十分复杂,电路响应与元件参数往往呈非线性映射关系,且电路中还存在非线性元件,使得实际应用中很难建立电路响应的精确数学模型[1,4−5];3)由于各类因素的影响,模拟电路非故障元件的实际参数值会在标称值上下随机波动,加之元件的非线性表征误差、测试误差等,使得诊断过程困难重重[1,4−6].
为解决上述关键问题,近年来国内外许多学者对模拟电路的故障诊断方法开展了研究,研究成果主要集中于模拟电路的故障特征提取和故障模式分类这两个关键环节上.在现阶段故障特征提取的研究中,模拟电路常用的故障特征主要有:1)在被测电路(Circuit under test,CUT)的内部测试节点直接测量节点电压作为故障特征[2,6−8];2)通过直流和交流分析从CUT的时频响应中提取的故障特征,包括峰值增益及对应的频率和相位[9]、直流输出电压和3dB截止频率等[10];3)通过信号处理得到的小波特征[1,11−12]、信号包络特征[5]及其他高阶统计量特征(如峰度、偏度、熵值等)[1,13−14].在故障模式分类的研究中,基于机器学习的故障分类方法是当前研究最多的方向,所用到的算法主要有:反向传播神经网络(Backward propagation neural network,BPNN)[4,9,14]、径向基网络(Radial basis function network,RBFN)[15]、支持向量机(Support vector machine,SVM)[4,16−17]、超限学习机 (Extreme learning machine,ELM)[18]等.此外还有基于故障编码[5]、类间距离[19]、贝叶斯法[16]等的故障分类器.然而,上述故障诊断方法存在三点不足:1)SVM、神经网络等分类算法的输出仅仅是故障样本对应的故障类别标签,无法输出其他诊断信息,如故障样本属于各故障类别的概率;2)在高维特征样本的分类器设计中,故障特征的维数约简与分类器建模是分离进行的,这样就存在约简后输入到分类器的特征与该分类器可能不是最佳匹配的问题[20];3)诊断实验中采用的故障多样性较少,难以代表实际应用中模拟电路的故障状况[4].
2001年Tipping[21]提出的相关向量机(Relevance vector machine,RVM)是一种基于贝叶斯框架的机器学习算法,相比SVM 具有参数设置简单、稀疏度更高、概率式输出、基函数不受Mercer条件限制等优点.但最初的RVM和SVM一样是为二分类问题设计的,在多分类问题中需要建立多个RVM分类器.2010年牛津大学的Psorakis等[22]在传统RVM的基础上提出了直接多分类相关向量机(Multiclass relevance vector machine,mRVM),通过采用Multinomial probit函数代替传统RVM 中的Logistic sigmoid函数从而将单个模型的二分类推广到多分类,并且能够给出分类结果的后验概率.此外,鉴于RVM 具有良好的稀疏性,文献[20,23−24]提出利用RVM进行特征约简,通过将线性核建立在原始特征空间并对特征维进行幂变换扩展,使之能对特征空间进行稀疏,从而得到最适合该RVM分类器的特征向量.然而幂变换扩展虽然保证了分类性能,但增加了模型训练的复杂度.
本文针对模拟电路故障诊断中的关键问题,提出了一种基于多核多分类相关向量机(Multi-kernel learning multiclass relevance vector machine,MKL-mRVM)的模拟电路故障诊断方法.所提方法沿用了文献[4]中的故障诊断实施框架,首先,通过故障注入技术来生成实际应用中可能出现的各类电路故障;然后,从频率响应中提取出用于诊断的最小模糊度特征(Minimum ambiguity features,MAF);最后,采用MKL-mRVM算法进行故障模式分类,MKL-mRVM能够对所提取的MAF的每一维建立非线性核,在保持原有分类能力的同时,通过约束核系数实现原始特征空间的稀疏化,得到一组更适合该分类器的稀疏特征向量,同时基于贝叶斯框架的MKL-mRVM还能够给出诊断结果的后验概率.Sallen-Key带通滤波电路和Biquad低通滤波电路是国际上最常用的两个验证诊断方法性能的基准电路,本文以这两个电路作为对象,验证所提方法的实用性.
本文的主要安排如下:第1节介绍了MKL-mRVM算法原理及训练流程,并分析了算法的计算复杂度;第2节介绍了模拟电路大规模故障诊断的实施框架,包括故障电路仿真、特征提取和故障分类的实现;第3节将所提方法应用到两个CUT的故障诊断实验中,并与其他方法进行了对比;第4节对文章进行了总结.
1 MKL-mRVM算法原理
1.1 MKL-mRVM模型
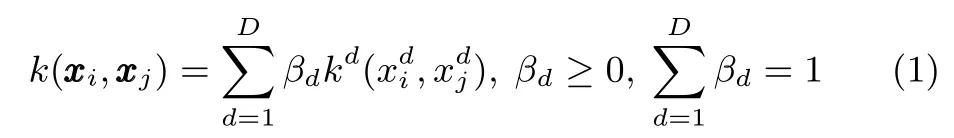
其中,kd为建立在每一维特征上的基本核函数,βd为基本核函数对应的加权系数,βd的大小反映了该特征对分类结果的贡献度.βd的值在模型训练中求出,若βd很小(如βd<10−10),则可认为该特征对于分类结果没有贡献,将其从特征空间中移除.
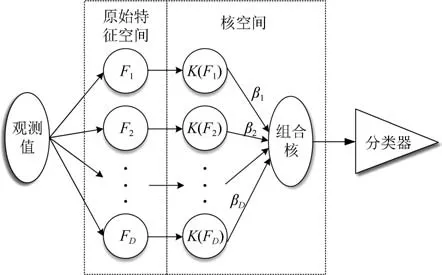
图1 多核组合原理图Fig.1Combination of multi-kernels
随后建立核矩阵K∈RN×N,K的每一列kn=[k(x1,xn),k(x2,xn),···,k(xn,xn)]T反映了在核函数映射下观测值xn与其他样本的关联性[22].mRVM引入了辅助变量Y∈RC×N来实现直接多分类,Y的概率分布与传统RVM的回归模型相同,即ycn∼N(wckn,1)[21],其中W∈RC×N为MKL-mRVM模型的权重.Y的大小可以看作样本所属类别的排位:对于观测值xn,ycn最大值所对应的类别c即为xn所属的类别,利用Multinomial probit函数[25]表示即为
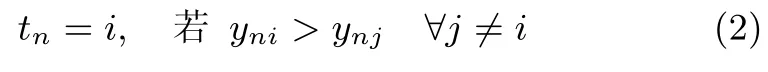
根据贝叶斯框架,为保持模型稀疏,为权重W设置先验分布,并令先验分布中的超参数αcn服从超参数为γ、ν的伽马分布.通过设置γ、ν取较小的值,训练后的权重W被约束在零点附近,使得模型为由极少数W为非零的相关向量(Relevance vectors,RV)组成的稀疏模型.记超参数αcn属于矩阵A∈RC×N,则采用了多层贝叶斯结构MKL-mRVM 模型结构由图2所示,其中,β和W是训练模型所要求解的变量,A、Y是求解过程的中间变量.由于引入了隐含变量Y,故参数求解采用了期望最大化(Expectation maximization,EM)算法.
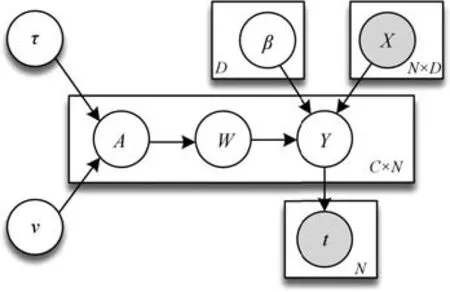
图2 MKL-mRVM模型结构示意图Fig.2Schematic diagram of MKL-mRVM
1.2 MKL-mRVM的训练
MKL-mRVM的训练是一个二型最大似然过程,训练过程迭代更新每个待求参数的值.在每一步迭代得到A的更新值后,采用EM 算法估计参数W、β、Y的更新值,其中M步估计W、β,E步估计Y.
首先求令边际似然函数p(Y|A)最大化的超参数A的估计值.假定样本n在各类别中共用一个超参数值αn,则超参数A的对数边际似然函数lnp(Y|A)可写为:
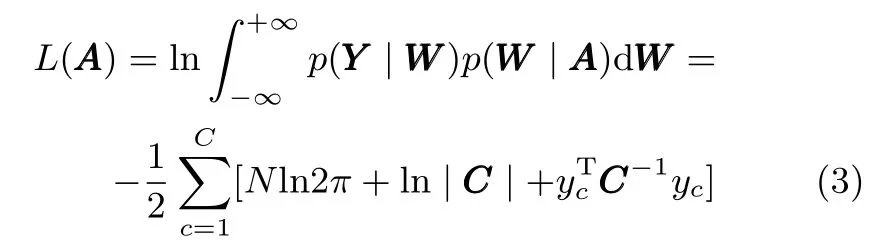
其中,C=I+KTA−1K,C∈RN×N.文献[26]分析了RVM训练单步迭代的计算复杂度,指出训练时若将包含了所有样本信息的整个核函数矩阵K代入模型会使算法的计算复杂度很高,因此采用了向模型中逐个添加样本的增量训练方式来训练模型.将C进行分解,得到:
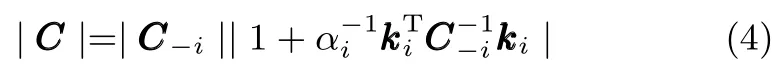
其中,C−i为隔离样本i之后的C,αi为样本i对应的超参数,ki为样本i所在的核函数序列.由此从L(A)中分解出样本i对L(A)的单独贡献值:
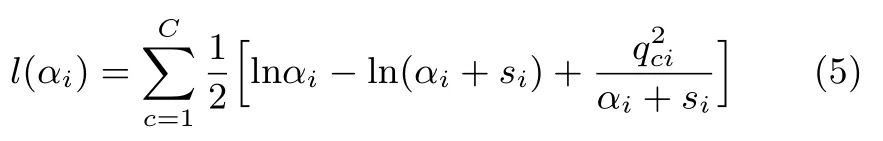
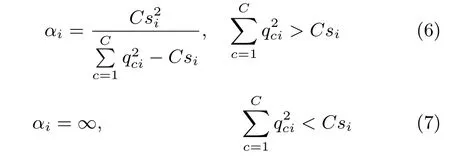
由此求得当前超参数矩阵A的更新值A∗,符号∗代表增量学习过程中模型当前包含样本数为M时的参数(M≪N),因此A∗∈RM×M,之后采用EM算法计算权重W的最大后验估计值:
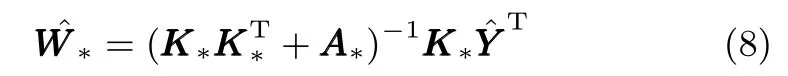
其中,K∗∈RM×N,为E步中隐变量Y期望的估计值.β的初始值为1/D,更新值通过求解式(9)的二次规划来得到.

最后根据M步W和β的估计值,给出E步中隐变量Y的期望的更新值.隐变量Y为C×N维锥形截断高斯分布,对于类别标签为i的样本,yin期望的估计值由式(10)更新;对于其他类别为c的样本(),ycn期望的估计值由式(11)更新[22].
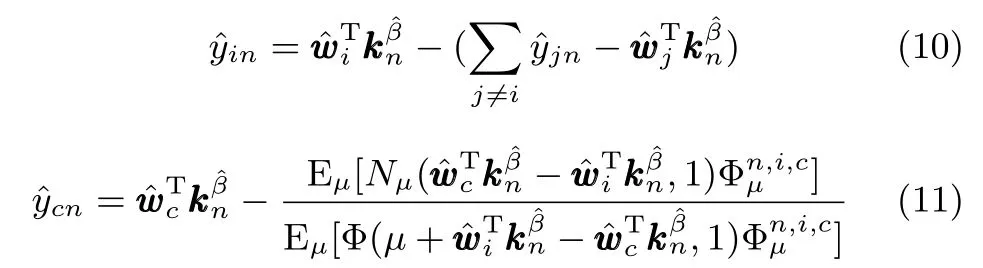
其中,µ服从标准高斯分布,µ∼N(0,1),Eµ[·]代表µ服从标准高斯分布时的期望,Φ代表高斯累积分布,定义为[22].
记X∗为包含在模型中的样本集合,训练开始令所有α=∞,此时X∗为空集,随后随机选择一个样本作为初始样本,为其超参数αi设置初始值
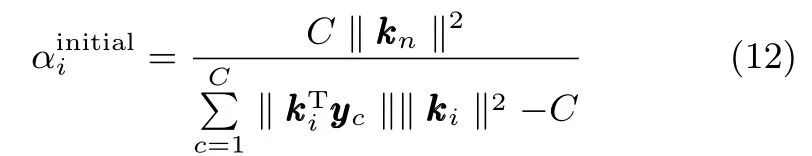
在随后的迭代中,根据选择的样本计算
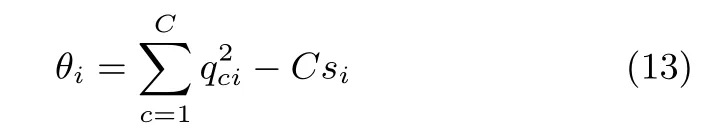
θi大小反映了该样本对模型分类提供的额外信息量[19].θi>0说明该样本对模型分类有益,需要将其加入X∗并更新αi的值;θi<0说明该样本为冗余样本,需要将其超参数设置为αi=∞使其从X∗中剔除.
当所有θi>0的样本均包含在X∗中且相邻两步迭代中超参数的改变值|lnAk−lnAk−1|<ε(ε通常取 10−12),则判定模型收敛.
综上所述,MKL-mRVM的迭代流程如下:
步骤1.初始化各模型参数:根据目标值t初始化Y,随机选择一个样本i并根据式(12)为其超参数αi赋值,令其他α=∞;
步骤2.更新超参数A∗:
a)根据式(13)计算样本的θi,
b)若θi>0,则根据式(6)更新αi,
c)若θi<0且αi<∞,则令αi=∞;
步骤3.M步:根据式(8)更新∗;
步骤4.求解式(9)的二次规划更新;
步骤5.E步:根据式(10)、(11)更新;
步骤6.再次随机选择一个样本,重复步骤2∼步骤5,直至满足收敛条件,训练结束.
1.3 MKL-mRVM的分类结果及计算复杂度
模型训练完成后,模型参数W和β中的大部分值为零,因此模型在样本空间和特征空间上均是稀疏的.对于新的输入样本xnew,MKL-mRVM的输出为一系列后验概率
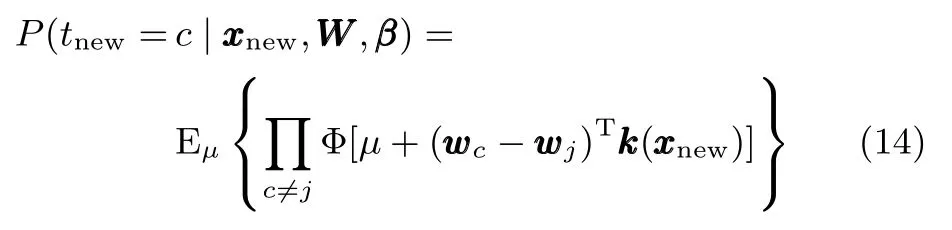
式(14)即新样本属于类别c的概率,而最大概率对应的类别即为新样本所属的类别
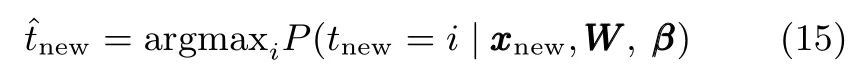
MKL-mRVM每步迭代的计算复杂度取决于三点:式(8)计算时的求逆运算、式(9)特征权值的优化以及式(10)、式(11)中更新值的估算.其中求逆运算的复杂度为O(M3),特征权值优化过程的计算复杂度取决于原始特征维数D,隐含变量更新值的计算复杂度主要取决于样本类别数C.此外,模型训练的迭代步数很大程度上由训练样本的数量决定,因此模型的总体训练时间取决于样本类别数、训练样本个数以及输入的原始特征维数.
2 模拟电路故障诊断的实施框架
本文所采用的模拟电路大规模故障诊断的实施框架源自文献[4],如图3所示.该框架分为故障电路生成、故障数据仿真、故障特征提取和故障模式分类4个阶段.
2.1 故障电路生成
模拟电路的故障通常可分为硬故障和软故障.硬故障(如开路或短路)会造成电路拓扑结构的改变,使电路功能发生很大变化;软故障指元件参数的实际值超出了容差范围,从而导致电路工作性能下降.
在故障电路生成阶段中,我们通过变异操作将多种故障注入到CUT中,得到一系列不同故障模式下的CUT变异体,故障生成所采用的变异操作见表1.其中,PCH为软故障变异操作,我们设置故障的最小可检测尺度(Minimum detectable fault size,MDFS)为2t(t为元件的容差值),采用均匀分布U(0.1Xn,Xn−2t)和U(Xn+2t,2Xn)(Xn为元件标称值)来分别表示元件的参数负向偏差(PCH↓)和参数正向偏差(PCH↑);ROP、LRB、GRB和NSP为硬故障变异操作,采用均匀分布U(100kΩ,1MΩ)和U(10Ω,1kΩ)来分别表示开路状态和桥接状态所用的阻值.
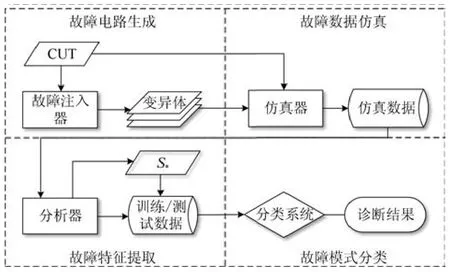
图3 诊断实施框架示意图Fig.3 Implementation framework of the diagnosis
2.2 故障数据仿真
将上一阶段生成的故障CUT变异体和初始的无故障CUT输入到基于Pspice内核的仿真器中,以扫频信号作为激励,得到各CUT的频率响应曲线的仿真数据.鉴于元件参数存在一定的容差,我们假设各元件参数服从均值为标称值Xn,标准差为σ=tXn/3的高斯分布,随后进行n次Monte Carlo仿真得到各类CUT的仿真数据n组.
2.3 故障特征提取
故障的特征值要满足:1)在同一故障中相近;2)在不同故障间不同[1].本文从CUT的频率响应曲线中提取了最小模糊度特征(Minimum ambiguity features,MAF)作为故障特征.
2.3.1 模糊度模型
设s为一故障特征值,由于s的大小会随着元件存在的容差而在一定范围内变动,故采用φ(s)来表示某一状态下s的概率分布.CUT所处的状态不同,对应的分布φ(s)也不同.对于指定的两类CUT故障fi和fj,定义二者在该特征下的模糊度为:
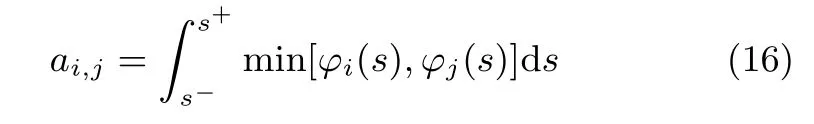
在实际计算中,我们采用核密度估计(Kernel density estimation,KDE)方法来求得故障特征值的概率分布函数.假设一组观测到的特征值,则采用KDE得到的概率分布函数为
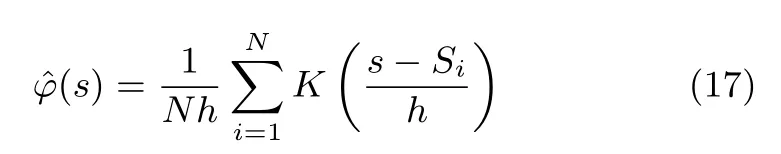
其中,K为核函数,h为平滑参数.
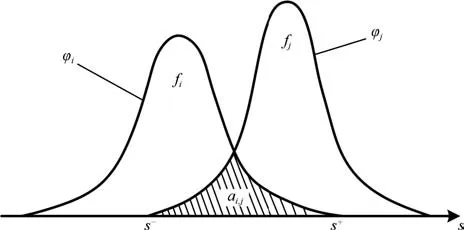
图4 模糊度示意图Fig.4 Schematic diagram of ambiguity
2.3.2 最小模糊度特征
从CUT的工作频率中采样得到m个离散的频率点作为特征集S={s1,s2,···,sm}, 每类故障都可得到一个基于该特征集的m×n维数据集Gm×n={G(s1),G(s2),···,G(sm)},n为故障数据仿真时的Monte Carlo仿真次数.
对于两类故障fi、fj及其对应的故障数据集Gi、Gj,首先计算二者的各特征下的模糊度,然后二者的最小模糊度特征可由式(18)得到[4]:
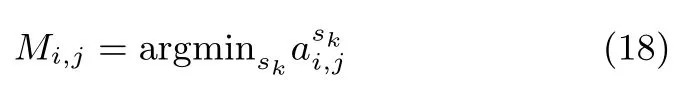
Mi,j∈ S,其对应的最小模糊度记作.通过各种故障两两之间的组合,可得到诊断任务所需的最小模糊度故障特征集S∗.
2.4 故障模式分类
根据最小模糊度特征集S∗生成训练数据集来训练MKL-mRVM 分类器,对于新的样本,MKL-mRVM 分类器能够输出该样本的故障类别、诊断置信度以及最优特征.诊断性能采用了文献[1]提出的以下5个指标来从多方面进行评价:

表1 变异操作Table 1 Mutation operators

3 诊断实验
本文的诊断实验包含两个案例:案例1为Sallen-Key带通滤波电路的诊断,注入故障数较少,主要用于详细分析MKL-mRVM算法的诊断性能;案例2为Biquad低通滤波电路的诊断,注入故障数较多,主要用于验证MKL-mRVM算法对大规模故障诊断的可行性.
为比较诊断结果,将同样采用核函数建模的SVM和核超限学习机(Kernel extreme learning machine,kELM)应用于故障模式分类中,三种方法均使用高斯核函数,并采用5折交叉验证法来选取平均验证误差最小的模型参数.其中,SVM采用一对一(One-against-one,OAO)法进行多分类,一共需要构建c(c−1)/2个SVM分类器.
仿真实验以Matlab 2015a作为实验平台,所有实验均在CPU为3.3GHz、内存为16GB的PC上运行.
3.1 Sallen-Key带通滤波电路诊断
3.1.1 实验设计
Sallen-Key带通滤波电路的电路结构如图5所示,其中心频率为25kHz.仿真实验注入14个软故障,故障描述见表2,其中,无故障状态下各元件参数的变动范围控制在容差的10%之内.
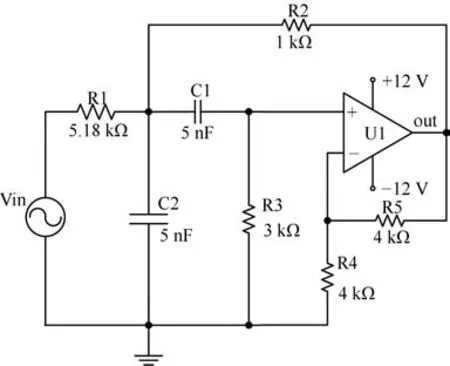
图5 Sallen-Key带通滤波电路结构图Fig.5 Sallen-Key band-pass filter circuit diagram
将从[0Hz,100kHz]频率区间中等间隔离散化得到的1001个激励信号输入到仿真器中,设置Monte Carlo仿真次数n=200,得到每类200个故障样本(共3000个).将故障样本按类别平均分为2组,第一组作为训练样本集,第二组作为测试样本集.
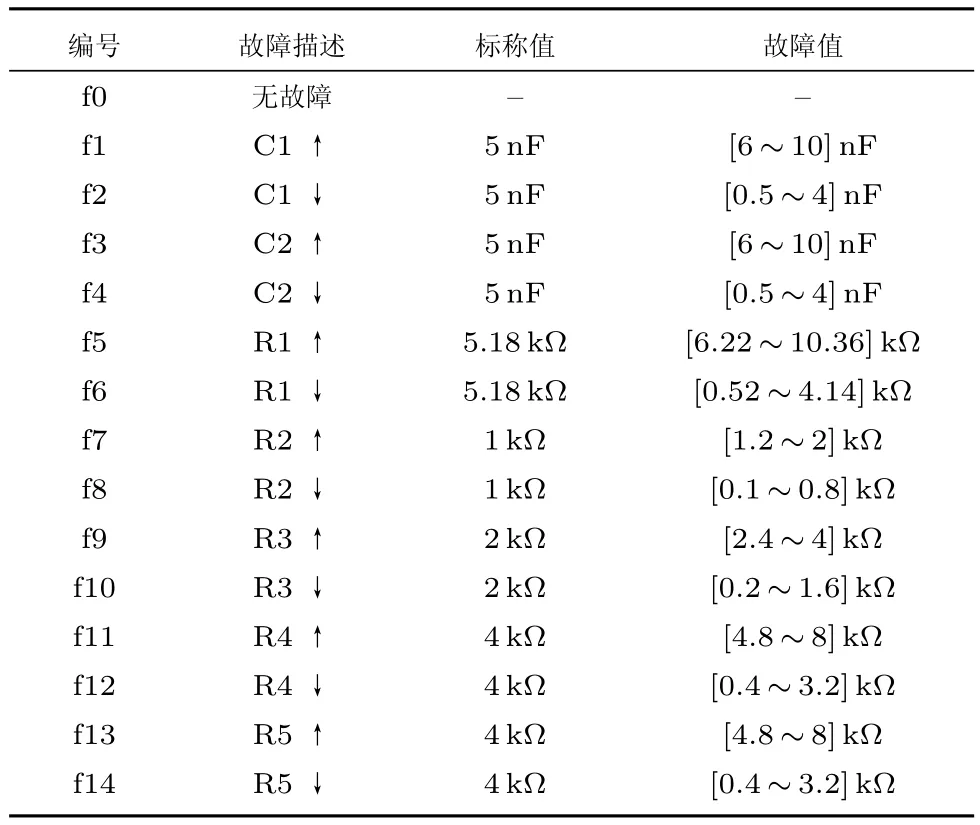
表2 Sallen-Key带通滤波电路故障描述Table 2 Faults in Sallen-Key band-pass filter
3.1.2 频率响应分析
图6给出了f1、f4、f5、f7 4类故障模式与无故障状态f0的频率响应曲线对比,可以看出在这4类软故障中,f5与f0的频率响应特性最为接近,二者在大部分频率点上存在重合,使得f5的诊断相对较难,余下三类故障模式与f0均在不同的频率区间上可分.
通过各类样本的模糊度分析,提取出该CUT故障的最小模糊度特征为S∗=0,3.9,9.0,10.6,11.2,12.5,16.0,16.8,17.0,19.5,20.8,23.9,25.7,26.1,33.4,34.8,48.5,78.2,91.7,97.6,100.0(kHz),共21个频率点.
3.1.3 诊断性能比较
表3给出了按照所选特征频率点三种方法的诊断性能及时间的比较,表中的粗体字代表了该项性能指标中的最好结果,其中测试时间为1500个测试样本的平均测试时间.通过表3可以看出:1)在诊断精度上,MKL-mRVM方法的精度最高,分类准确度能够达到96.40%,SVM 次之,略高于kELM;2)在训练时间上,kELM拥有最快的训练速度,SVM次之,而MKL-mRVM 的训练时间高达381.4s,这是由于MKL-mRVM较多的迭代步数极大地增加了总体训练时间,图6显示了MKL-mRVM的训练过程,算法在迭代1502步后收敛,迭代步数几乎等于训练样本数;3)在平均测试时间上,kELM依然拥有最快的速度,SVM次之,MKL-mRVM略慢于SVM,这是由于MKL-mRVM 在测试中需要计算样本属于各类别的概率,而概率信息对于诊断结果的评价具有重要作用.

表3 三种方法的诊断性能对比Table 3 Diagnostic performance comparison of 3 methods
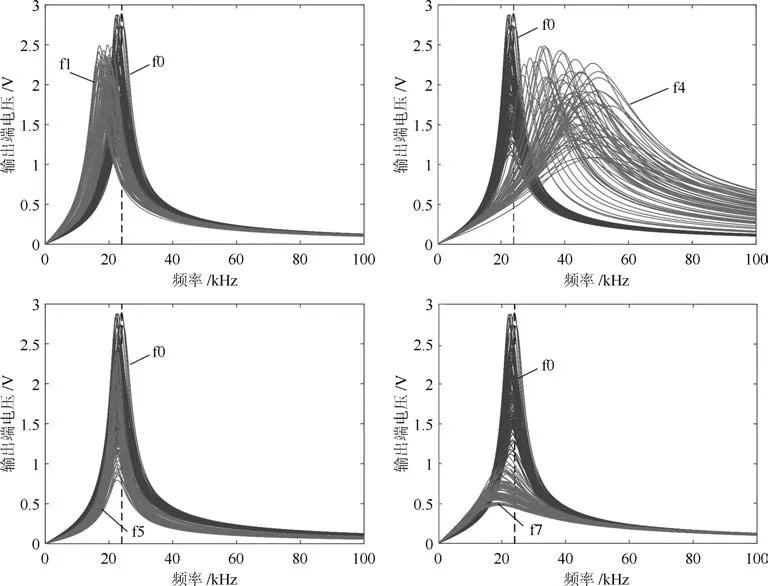
图6 几类故障的频率响应曲线Fig.6 Frequency response curves of faults
在MKL-mRVM的诊断结果中,所有故障模式里诊断正确率最低的是f5,对应的正确率为89%,诊断正确率最高的是f4,对应的正确率为98%,从诊断结果来看,MKL-mRVM对本案例中的各类故障模式均有较好的区分能力,并且诊断正确率和该故障模式与其他故障模式频率响应的相似度相关,频率响应曲线越相似,诊断的正确率越低.
虽然MKL-mRVM 的训练时间较长,但其构建分类模型实际用到的样本很少.由图7可以看出,由于采用了增量训练方法,MKL-mRVM在每一步迭代中仅对1500个训练样本中的1个进行学习来更新超参数矩阵A∗,并根据更新后的α值来判断该样本是否保留在模型中.当算法收敛时,原有1500个训练样本中的绝大多数样本的超参数α=∞,仅保留了其中15个α<∞的样本作为相关向量来构建分类模型,因此在实际使用中可通过减少训练样本的数量来减少模型的训练时间.文献[27]提出了一种用于传统RVM的训练样本集精简方法,其基本思想利用Gram-Schmidt算法检测样本之间的线性相关性,从而剔除样本集中的冗余样本点,理论上可以应用到MKL-mRVM中.此外,对于已经训练好的MKL-mRVM 分类模型,若有新的故障样本出现,MKL-mRVM能够在原有分类模型的基础上通过增量训练对新样本进行单独学习,通过算法流程的步骤2∼5来快速更新模型参数,无需纳入之前的所有样本重训模型,使得MKL-mRVM可以应用到样本序贯输入的在线诊断中.
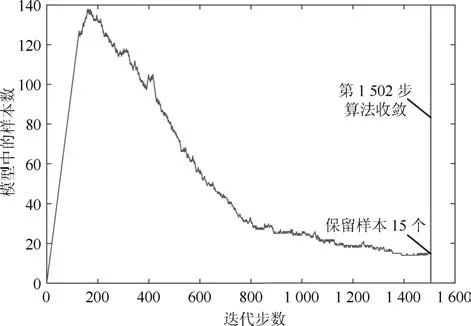
图7 MKL-mRVM的迭代过程Fig.7 Diagnostic performance comparison of 3 methods
3.1.4 特征选择及分类置信度分析
MKL-mRVM算法在输入的21个原始故障特征上建立了基本核函数,基本核函数的加权系数β可以表示故障特征对分类的重要程度.图8显示了模型训练后加权系数β的大小,可以看出,大多数的加权系数都在10−10以下,对应的特征为无关特征,将其从模型中剔除,剩下系数较大的7个特征被认为是重要特征,即MKL-mRVM所选择的最能代表故障特点并将各类故障进行区分的频率点最小集合.根据训练结果,本案例的最优特征集为Sopt=0,10.6,11.2,12.5,20.8,23.9,100.0(kHz).
MKL-mRVM分类器能够输出测试样本属于各类别的后验概率,因此可将分类结果对应的概率大小作为诊断结果的置信度.为分析诊断结果与置信度的关系,我们从正确诊断的样本和错误诊断的样本中各随机挑选20个样本,所选样本的诊断结果与诊断置信度的关系如图9所示.可以看出,诊断正确样本的诊断置信度明显高于诊断错误样本的诊断置信度.在本案例的所有测试样本中,诊断正确的样本平均诊断置信度达到0.8505,而诊断错误的样本平均诊断置信度仅为0.4103.因此,MKL-mRVM所输出的概率信息能够对诊断结果的质量进行评价,具有一定的实用价值.
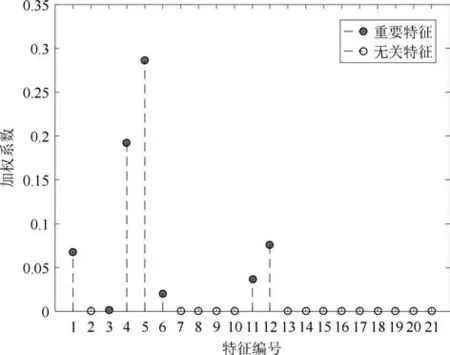
图8 故障特征对应的加权系数值Fig.8 The weighting factors of fault features
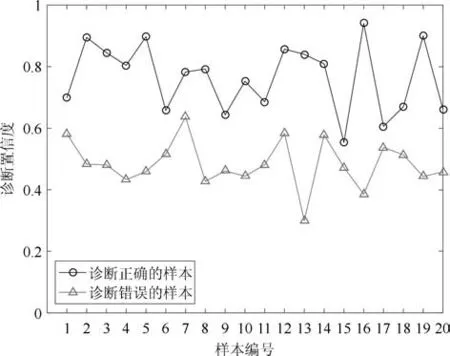
图9 诊断结果的置信度Fig.9 Confidence of diagnostic results
3.2 Biquad低通滤波电路诊断
3.2.1 实验设计
Biquad低通滤波电路的电路结构如图10所示.该电路包含较多的元件数量,仿真实验共注入各类故障92个,详见表4,其中,软故障PCH↓和PCH↑对应的元件参数服从均匀分布U(0.1Xn,Xn−2t)和U(Xn+2t,2Xn),硬故障中,ROP、NSP接入的阻值服从均匀分布U(100kΩ,1MΩ),LRB、GRB接入的阻值服从均匀分布U(10Ω,1kΩ).
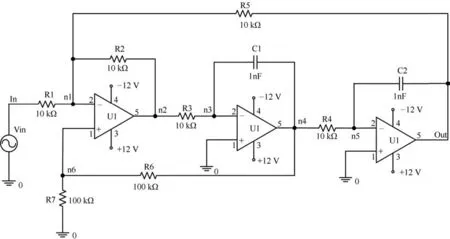
图10 Biquad低通滤波电路结构图Fig.10 Biquad low-pass filter circuit diagram
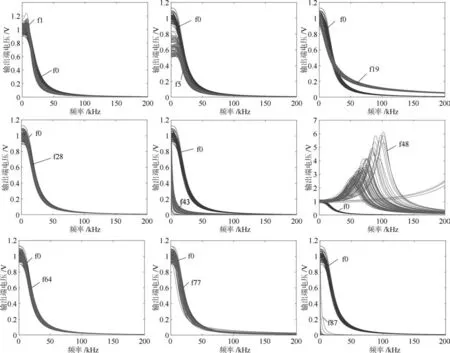
图11 几类故障的频率响应曲线Fig.11 Frequency response curves of faults
将从[1Hz,200kHz]中等间隔离散化得到的1000个激励信号输入到仿真器中,设置Monte Carlo仿真次数n=100,得到每类100个故障样本(共9300个).同样按类别将其平均分为2组,分别作为训练样本集和测试样本集.
3.2.2 频率响应分析
图11给出了9类故障模式与无故障状态f0的频率响应曲线对比,可以直观的看出f5、f19、f43、f48、f87 5类故障在所选频率区间内与f0有很好的可分性,f1与f0在部分区间内可分,而f28、f64、f77与f0的频率响应极为相似,四者在绝大部分频率点上重合.根据模糊度分析本案例共提取出NS∗=350个最小模糊度特征.
3.2.3 诊断性能比较
由于许多故障模式的频率响应曲线和无故障状态的频率响应曲线过于相似,使得分类器根据所选的特征频率点依然难以精确地诊断出每类故障.因此,对于表4中的各类故障我们设置不同模糊组门限λ来给出故障所属的模糊组.图12给出了无故障状态f0所对应的模糊组,图中λ所在圆的内部所有的故障两两互为模糊组,当λ=1时不存在模糊组,随着λ减小,越来越多故障表现相似的故障类型落入到同一模糊组中,可以看出图11中f28、f64、f77三类难以区分的故障均在f0的模糊组中.表5给出了不同模糊组门限λ下三种方法的诊断性能,在存在模糊组的前提下,只要诊断结果为实际故障所在模糊组中的任意一种故障我们就假定诊断正确.
通过表5可以看出:1)当λ=1,即不考虑模糊组的情况下,三种方法的分类准确率都比较低,同时故障误判率也非常高,这是由于多种故障的频率响应曲线和f0非常接近,分类器难以将正常状态从多类故障状态中区分出来,随着λ降低,征兆相似的故障故障不断落入同一个模糊组中,在考虑模糊组的情况下,三种方法的分类准确率也随之上升,当λ<0.5时,MKL-mRVM的分类准确率能够达到85%以上;2)在不同模糊组的诊断中,MKL-mRVM均拥有最高的分类准确率,SVM次之,kELM最低,MKL-mRVM在λ=0.3时的分类准确率就已经高于λ=0.1时SVM和kELM的分类准确率;3)kELM 依然拥有最快的训练速度和测试速度,而MKL-mRVM的训练和测试速度最慢,模型的训练花费了近6个小时,较多的故障类别和特征维数大大增加了MKL-mRVM的训练时间.
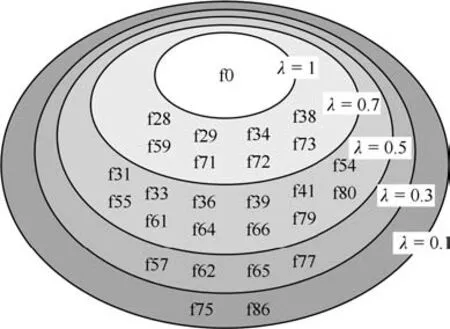
图12 不同门限下f0所在的模糊组Fig.12 Ambiguity groups of f0 under different thresholds
3.2.4 采用其他特征的诊断性能
虽然较多的训练样本数以及特征数极大地增加了MKL-mRVM的训练时间,但MKL-mRVM从350个特征中提取了47个作为诊断的最优特征,由于冗余信息被剔除,MKL-mRVM的分类准确率明显高于SVM和kELM.为比较故障特征以及最优化约简对诊断性能的MKL-mRVM影响,表6给出了不考虑模糊组(λ=1)的情况下分别采用高阶统计量(峰度结合偏度)[13]、电路规格参数(峰值增益和3dB截止频率)[14]以及未经约简的MAF作为特征时mRVM的诊断性能(由于不需要特征约简故采用mRVM),可以看出,相比本文提出的诊断方法,高阶统计量和电路规格两种特征虽然计算复杂度小,但诊断精度却远远低于本文方法,难以应对大规模故障诊断的需求,而未经约简的MAF虽然使得训练时间得以缩短,但诊断精度不及本文所提方法.此外,尽管本文所提方法提高了故障诊断的准确率,然而当充分考虑现实中可能存在的各类故障时,上述方法都难以取得比较理想的诊断精度,在大规模故障诊断中依然存在着许多模糊组.
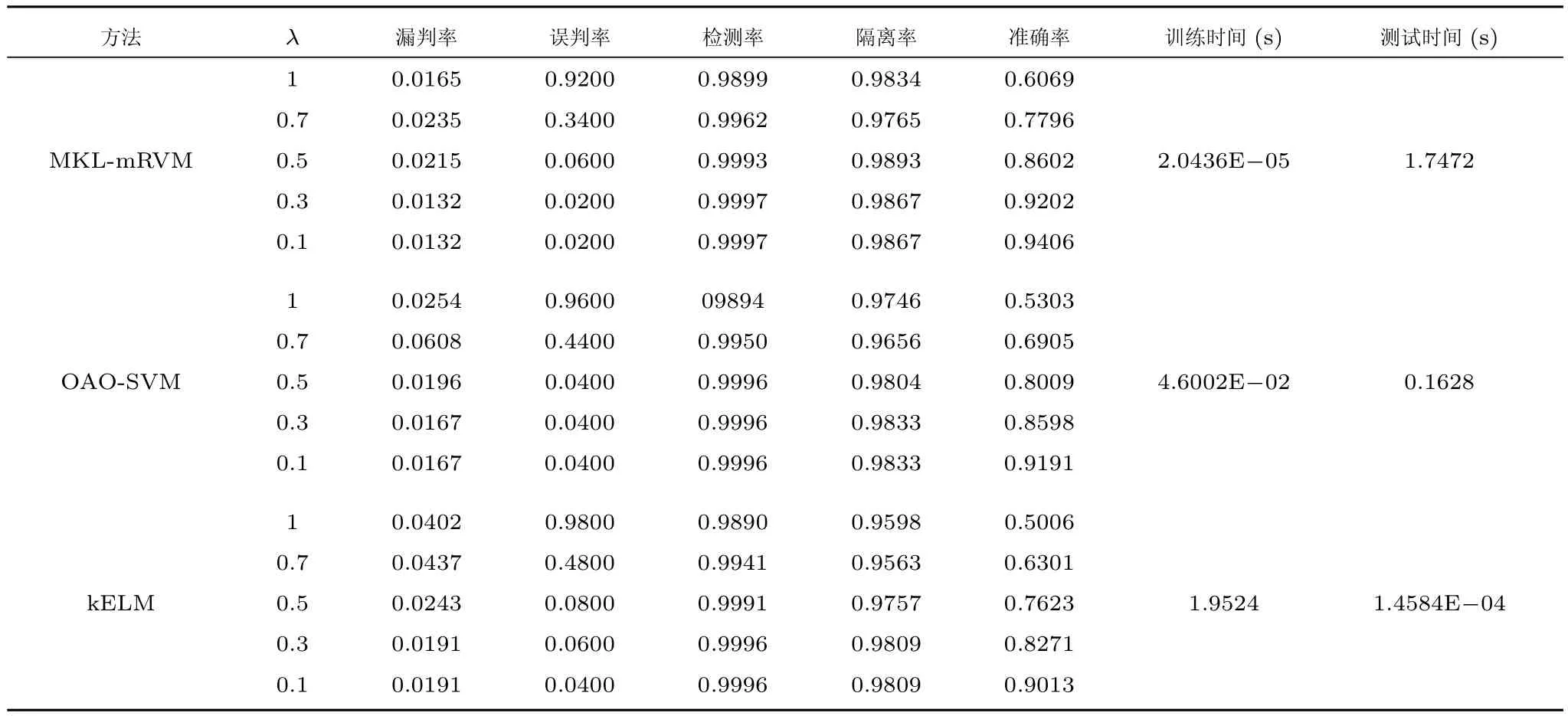
表5 三种方法的诊断性能对比Table 5 Diagnostic performance comparison of 3 methods
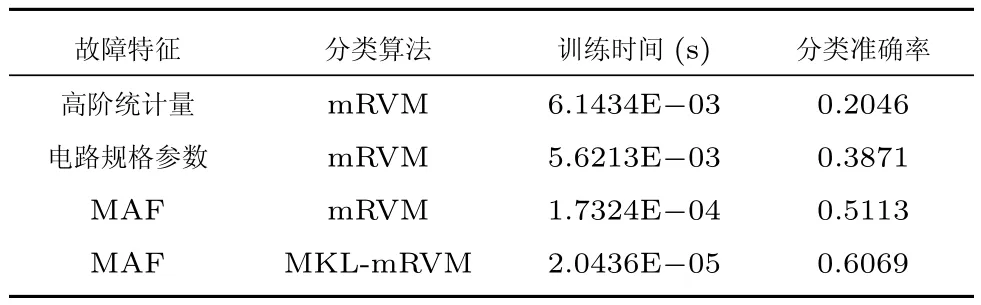
表6 其他特征的诊断性能Table 6 Diagnostic performance of other features
4 结论
本文提出了一种基于MKL-mRVM的模拟电路故障诊断方法,相比已有方法,本文方法的主要贡献有:1)通过故障注入生成了参数连续的软故障和各类硬故障,并考虑了非故障原件的参数容差,使故障样本更贴合实际情况;2)MKL-mRVM能够约简原始故障特征,减少冗余信息,使得故障诊断结果的准确度更高;3)基于贝叶斯框架的MKL-mRVM分类算法能够给出诊断结果的置信度.然而模拟电路的故障诊断是一个复杂的问题,本文所提方法在应对大规模故障诊断时依然达不到理想的诊断精度,诊断结果依然存在着较多的模糊组,并且MKL-mRVM用于诊断时的训练时间较长,下一步的研究工作可集中于提高MKL-mRVM的训练效率.
