基于半参数CARE模型的金融市场VaR度量
2019-04-12胡宗义唐建阳
胡宗义,李 毅,万 闯,唐建阳
(1.湖南大学 金融与统计学院,湖南 长沙 410079;2.厦门大学 邹至庄经济研究中心,福建 厦门 361005)
一、引言
寻找一种有效的风险度量手段对股票市场健康、平稳地运行至关重要。回首过去,中国股票市场的多次大起大落仍历历在目,相比于发达国家日臻成熟的金融市场,中国正处在蹒跚学步不断探索的阶段。在此情况下,一种有效的风险度量手段对中国股票市场来说就显得尤为迫切。近年来,有关度量和管理市场风险的理论和方法如雨后春笋层出不穷,其中“在值风险(Value at Risk,简称VaR)”理论被广泛应用。VaR指的是在一定的置信水平下,某一时期内持有某种证劵或资产组合可能发生的最大损失[1]25-30。由于采用VaR度量风险,运算简单且便于理解,因而备受学者青睐。然而,传统的VaR计算方法是以分位数理论为基础,没有充分考虑资产组合的总体信息,而只是利用分布中的部分信息[2]。事实上,任何一个风险管理者都希望能充分利用资产组合的损益信息,从总体上度量风险大小。基于此,Kuan等提出一种基于Expectile的风险度量工具(Expectiled-based Value at Risk,简称EVaR),与VaR相比,EVaR具有能有效利用总体信息和对尾部损失分布的大小更加敏感等优势[3]。Expectile的概念由Newey等提出,它具备以下优点:第一,Expectile强调全局性,可以完全利用分布的总体信息;第二,Expectile中二次平方损失函数不仅使计算更加方便快捷,而且提高了估计精度[4]。目前,有关EVaR的研究大多基于参数模型,Kuan等首次提出参数化的条件自回归Expectile(CARE)模型,运用非对称最小二乘法(ALS)对模型参数进行估计[3];钱夕元等采用参数化CARE模型计算国内外五种指数的VaR并与GARCH和SV模型估计结果做对比,结果表明基于参数化CARE模型并不能很好地刻画市场风险[5]。谢尚宇等将CARE模型应用到带有异方差的数据,通过引入ARCH效应提出线性ARCH-Expectile模型,采用两步估计法对模型参数进行估计[6]。参数模型是对整个收益分布进行建模,需要对收益分布提出众多假设条件以保证模型参数估计的准确性。然而,在实际应用中很多假设是不成立的。
基于此,本文拟采用半参数模型度量中国股票市场的VaR。与参数模型相比,半参数模型直接对VaR时间序列进行建模,无需对收益分布进行假设。Engle等提出半参数化的条件自回归模型[7],模型参数估计采用分位数方法,本文在此基础上利用Expectile对模型参数进行估计,得到基于半参数的条件自回归模型(CARE)的风险度量方法。为验证半参数CARE模型对中国股票市场风险度量效果,本文选取中国股市的上证综指(SH)和深圳成指(SZ)为研究对象,并与经典的基于GARCH模型风险度量方法进行对比。
二、半参数CARE模型的设定与估计(一) 基于Expectile的VaR估计
VaR凭借其简单实用、便于操作的特点,已成为众多商业机构和风险管理人员衡量市场风险的重要工具。Jorion给出VaR的数学表达式:VaR(α)=-q(α),其中,α为显著性水平,q(α)为α分位数下Y的资产收益率。q(α)通过最小化非对称绝对偏差函数获得,具体表达式如下:

(1)
其中,I(·)表示指示函数。对式(1)的正则方程变形可得:
(2)
式(2)表明VaR的大小只依赖于极端损失的概率,而与损失规模的大小无关。由于基于分位数的VaR对极端损失大小的不敏感性,使其在评估尾部风险时具有严重缺陷[3]。与式(1)绝对偏差不同,Newey等考虑了一类非对称平方损失函数[8]:
E[ρω(Y-m)]
=E[|ω-I(Y≤m)|·(Y-m)2]
(3)
其中,ω∈(0,1)反映了边际损失的非对称程度,称为谨慎性水平(prudentiality level),Newey等人将其定义为Expectile回归。由于二次损失函数是可微的,对式(3)求一阶导数,可得:


(4)
进一步计算可以推出:
(5)
从式(5)可以看出基于Expectile计算的VaR不仅与分布的尾部概率有关,而且还依赖变量的取值,因而对尾部损失规模大小更加敏感。为便于理解,将式(4)转换成如下条件均值形式。
m(ω)=γE[Y|Y>m(ω)]+
(1-γ)E[Y|Y≤m(ω)]
(6)
其中,γ=ω[1-F(m(ω))]/{ω[1-F(m(ω))]+(1-ω)F(m(ω))}为Y>m(ω)的权重。因此,m(ω)可以理解为条件上端均值E[Y|Y>m(ω)]和条件下端E[Y|Y≤m(ω)]的加权平均。当ω<0.5时,EVaR为一致性风险度量工具[9]。
实际上,Expectile与分位数之间存在着一一对应的关系[10]。对于任意ω,存在α∈(0,1)使得q(α)=m(ω),那么ω便可用下式表达:
(7)
(二)模型设定
一般的参数模型在计算VaR时,通常假定收益回报的条件分布函数服从位置—尺度函数,具体表达式如下:
VaRt(α)=-mt-q(α)σt
(8)
其中,mt和σt分别是收益率rt的条件均值和标准差,q(·)是相对应的分位数函数。
CAViaR与一般的参数模型不同,它不是对条件方差进行建模,获得单个VaR的估计,而是对整个VaR序列进行建模。不同的金融市场,其市场行为和波动的特征千差万别,VaR的变化规律也不一样。因此,Engle等提出以下几种模型形式来刻画不同类型的市场。
对称绝对值模型(SAV):
VaRt=β0+β1VaRt-1+β2|yt-1|
(9)
非对称斜率模型(AS):
VaRt=β0+β1VaRt-1+β2(yt-1)++β3(yt-1)-
(10)
其中,(x)+=max(x,0),(x)-=-min(x,0)。
间接GARCH(1,1)(IG):
(11)
王新宇等在研究中国股市的过程中,对CAViaR模型进行了补充了,又提出了一种新的模型形式[11]。
间接TARCH模型(IT):
VaRt=β0+β1VaRt-1+β2(|yt-1|-β3yt-1)
(12)
其中,β3取值范围为(-1,1)。间接TARCH-CAViaR模型既考虑了VaR调整的预期,即VaR的滞后阶,同时也反映了过去的收益信息对VaR的影响,尤其当这种影响是非对称的情形。
根据以上CAViaR模型的结构,可以推导出基于半参数的CARE模型的形式。以对称绝对值模型(SAV)为例进行说明,对于另外三种模型对应的具体形式可以此类推。
EVaRt=β0+β1EVaRt-1+β2|yt-1|
(13)
(三)模型估计
采用非对称最小二乘法(ALS)估计半参数CARE模型。Engle等使用遗传算法求解CAViaR模型,大致过程如下:首先,从(0,1)或(-1,0)的均匀分布中产生105组参数向量,计算每组参数在模型下的QR值;然后,选取其中十组具有最小QR值的参数向量作为quasi-newton算法的初始值进行迭代;最后,达到迭代满足条件,便可获得十组参数估计值及其相应的QR值。模型的最终估计值为这十个QR值中最小值所对应的参数估计向量。半参数CARE模型的求解以该方法为蓝本进行局部修改,将计算QR值转化成计算ALS值,再进行迭代求解即可。
模型建立后,需对模型的稳健性进行检验。本文将VaR模型中常用的几类常返检验(back testing)运用到CARE模型的检验中,分别给出了动态分位数回归检验、非条件和条件覆盖检验以及独立性检验四种统计量。采用Engle等提出的动态分位数回归(Dynamic Quantile Test,简称DQ)检验评估模型设定的合理性[9],同时比较ALS值及样本外失败率(failure rate)的大小评估预测结果的准确性。其中,对于DQ检验所要构建的人工回归方程,回归变量应包括常数项、前五个滞后项冲击值以及当期的VaR预测值。另外,采用Kupiec提出的非条件覆盖(unconditional coverage)检验评估EVaR估计的有效性和准确性[12]。为检测冲击序列的独立性,本文采用Christoffersen提出的独立性检验和条件覆盖检验[13]。
三、实证分析(一)样本的选取及描述
选取深圳成指与上证综指作为研究对象,时间范围为2003年1月3日到2015年12月31日,共计2 654组数据。在这期间,中国股市先后经历股权分离改革、金融危机以及欧债危机等几次重大事件,股市波动较大,对此次研究结果具有较好的对比效果。将样本分成两部分,前面2 654组数据作为估计样本或建模样本,称为样本内观测值,最后的500个数据作为预测和检验样本。数据来源于网易财经历史数据库。考虑每种股指每日收盘价的对数收益率yi,t,计算公式为:yi,t=ln(Pi,t)-ln(Pi,t-1),其中,Pi,t为i指数第t天的收盘价。
表1概括了两种股指内外样本的基本的统计信息。由峰度参数可得出每种指数的收益率时间序列都呈现左偏特征。JB统计量均显著地拒绝正态分布的原假设。此外,Ljung-Box Q(10)统计量表明在5%显著性水平下,两种指数的内外样本均不存在序列相关性。两种指数的ADF检验均表明其为平稳的时间序列,可以进行进一步地分析。
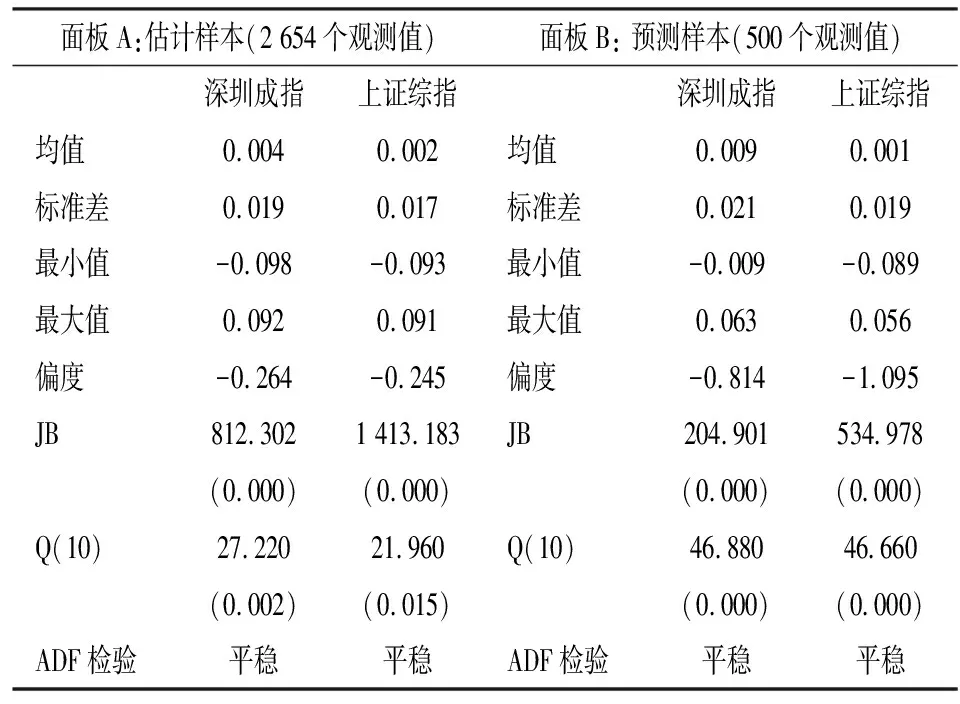
表1 深圳成指和上证综指日对数收益率的描述性统计表
注:括号内表示p值;Q(10)表示日对数收益率的10阶序列相关Ljung-Box Q统计量。
(二)金融市场VaR度量结果分析
给定置信水平为95%和99%,分别对两种指数的VaR进行建模。采用Expectile估计VaR时,首先要选择合适的ω使得低于ω-expectile值的样本占总样本的比例为α,这里的α=1%、5%。由于不对收益的分布做任何假设,即收益的分布类型未知,利用式(7)求ω值是行不通的。所以,本文采用网格搜索法来确定两种指数在不同模型下的ω值,其结果见表2。

表2 给定α分位数水平下对应的ω(×100)
选取前2 654组数据作为估计样本,时间区间为2003年1月3日到2013年12月18日,模型参数的估计结果见表3和表4。2013年后,中国股市经历一次较大的波动,收益率呈现出聚集现象。本文为检验半参数CARE模型在这种金融环境下的预测行为,采取向前一步滚动预测法,根据前面样本内的已估参数模型对后面500个样本外的观测值进行预测,得到了置信水平为95%和99%的VaR预测序列。
为验证半参CARE模型的有效性,本文选择常用的GARCH模型与半参数CARE模型进行对比。GARCH模型是Bollerslev提出,可以用来刻画资本收益时间序列中条件异方差性,常见的收益序列服从高斯分布、学生t分布或者广义误差分布[14]。然而,由表1可知JB检验统计量的p值接近于0,即在1%的显著性水平下,两种指数不满足正态性假设。所以,本文只考虑服从学生t分布的GARCH模型。表1中证明了两种指数均呈现左偏的特征,本文同样引入标准有偏t分布的GARCH模型。将上述两种GARCH模型分别记为GARCH-t和GARCH-SKEWt。对于GARCH类模型的参数估计问题,本文采用R软件fGarch软件包的garchFit命令求解。
采用GARCH模型进行预测,允许模型的参数随着时间的变化而变化。在本文的实证中,选取固定窗宽为2 654的滚动窗口预测法预测两类指数的样本外的VaR和ES,即选取前面2 654个数据作为初始预测样本,通过向前增加下一日的观测值到滚动样本内,不断更新模型的参数,这样便可得到500组向前一步的VaR预测结果。

表3 半参数CARE模型的参数估计值表(α=1%)
注:括号中的数值为p值。

表4 半参数CARE模型的参数估计值表(α=5%)
注:括号中数值为p值。
(三)模型选择
当模型构建完成后,一个重要的目的就是对中国股指进行预测,那么应该如何选择一个合适的预测模型?本文提出的选择策略是,首先剔除没有通过DQ检验的模型,再按ALS或样本外的失败率最小值原则进行选择。同时也要通过非条件覆盖检验、独立性检验和条件覆盖检验。表5和表6分别给出两种指数在不同模型样本外DQ检验的p值,ALS值以及失败率。
由表5可知,选择深圳指数的最优VaR(α=1%、5%)模型。当α=5%时,根据DQ检验的原则,剔除IGARCH-CARE模型与两类参数GARCH模型。SAV、AS、ITARCH-CARE模型的DQ检验所对应的p值分别为0.053、0.051、0.051,表示都通过DQ检验,且另外三种检验也都通过。这说明半参CARE模型都能较好地预测深圳股票市场风险。但是,AS-CARE模型的失败率和ALS值都显著低于其他模型,因此AS-CARE模型为深圳指数5%VaR最优预测模型。当α=1%时,在置信显著性水平为95%的情形下,四类半参数CARE模型均没有通过DQ检验,首先予以排除,同理,GARCH-t模型也要排除。不难发现GARCH-SKEWt模型的DQ检验统计量p值为0.999接近于1,这说明GARCH-SKEWt模型可以完美地刻画深圳指数VaR未来的波动。因此,选择GARCH-SKEWt模型为深圳指数1%VaR的预测模型。
由表6可知,对于上证指数VaR,当α=5%时,SAV、IGARCH-CARE和GARCH类模型均通过DQ检验,它们的p值分别为0.074、0.133、0.059、0.059。但是,GARCH-t模型的失败率为0.052,ALS值为0.043,均达到了最小的原则。因此,GARCH-t模型可以很好预测上证指数5%VaR的变动。当α=1%时,SAV、IGARCH-CARE、GARCH-t和GARCH-SKEWt模型均在1%显著性水平下通过DQ检验,且失败率均为0.018,此时只有根据ALS最小值原则选取模型,而SAV-CARE模型的ALS值最小为0.016,远低于GARCH模型。因此,SAV-CARE模型适合预测上证指数1%VaR的波动。
通过对中国股市的分析可以得出半参数CARE模型与GARCH类模型,对于不同指数的适用程度是不同的。GARCH模型作为经典的风险度量模型展示了其强大的适用性,而半参CARE模型也有其独特的优势。半参CARE模型作为新的风险度量方法,是对中国股指风险度量的一个很好补充,为相关的金融机构和风险管理者提供一个新的研究视角。
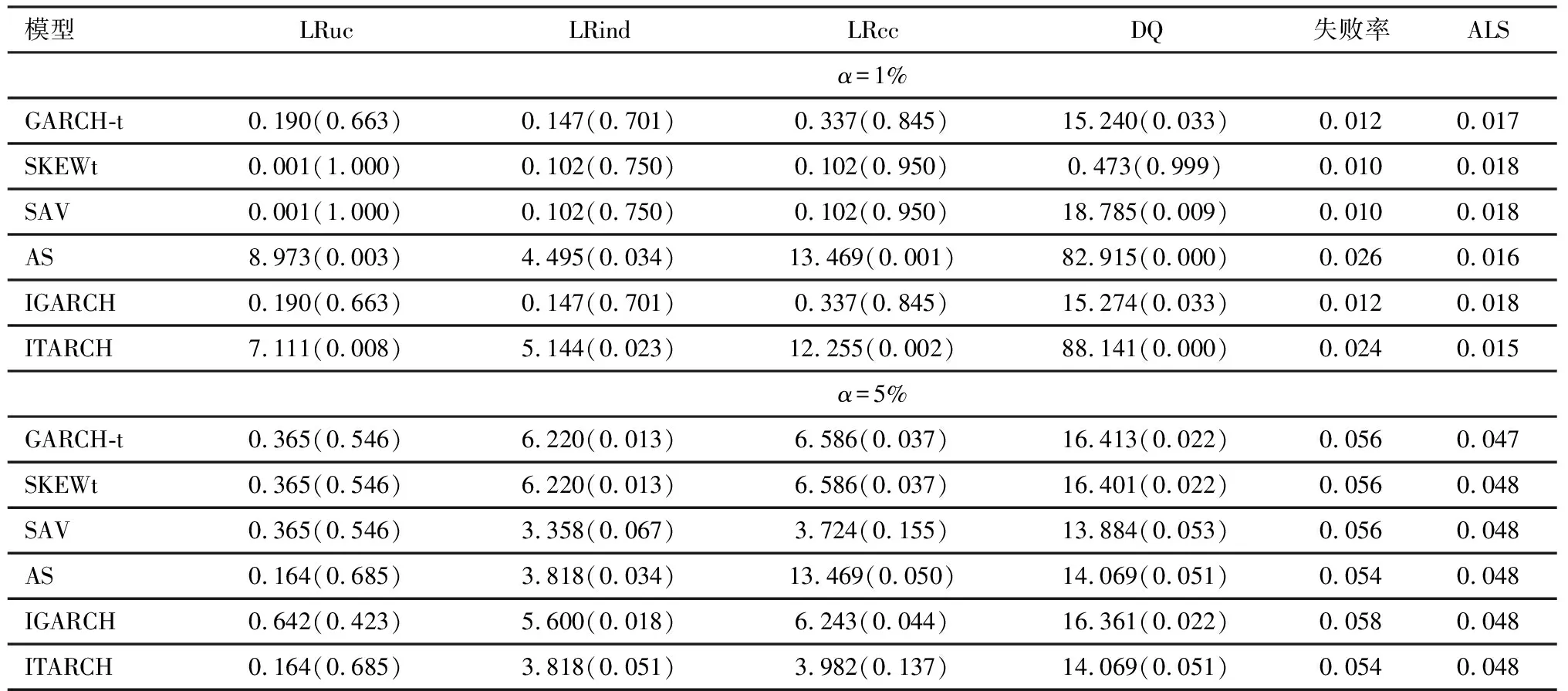
表5 深圳成指的模型对比检验结果表
注:括号中数值为p值。
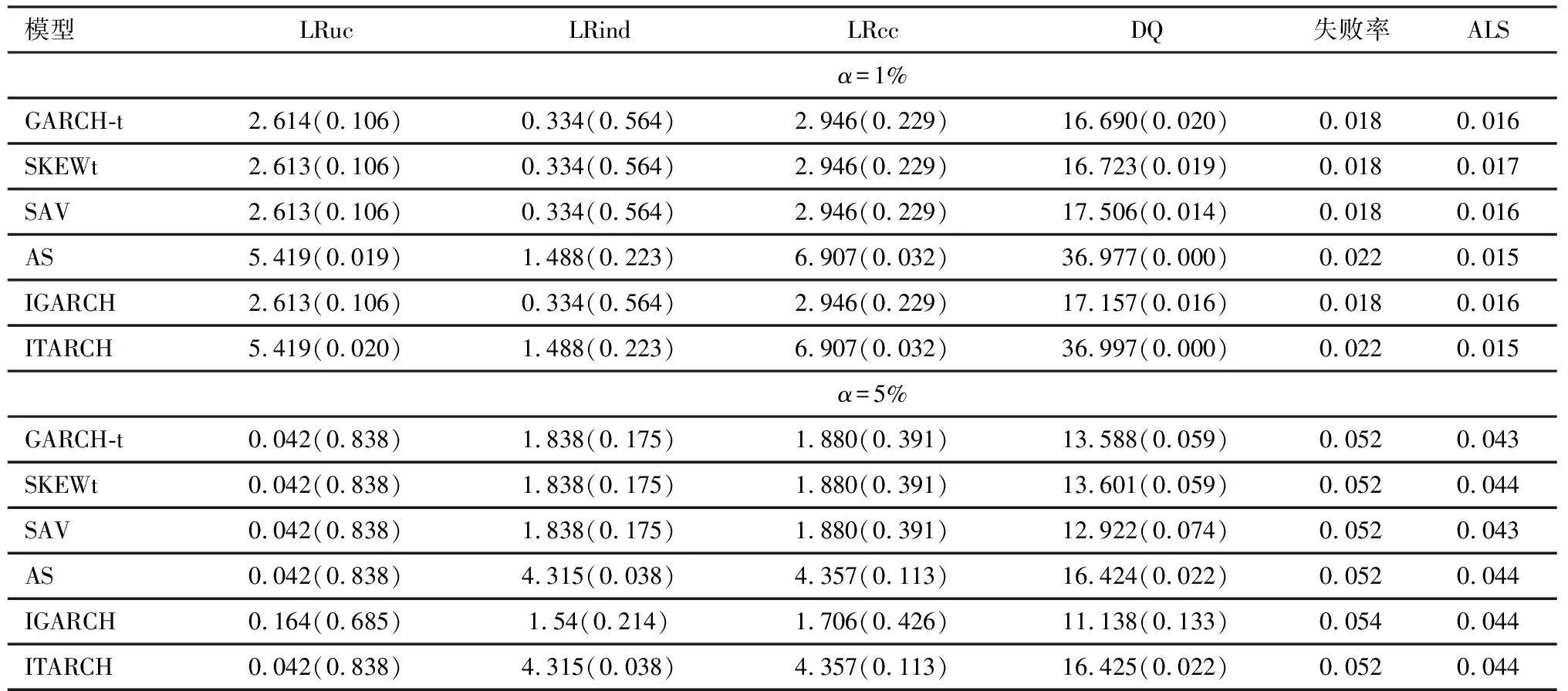
表6 上证综指的模型对比检验结果表
注:括号中数值为p值。
四、 结论
本文介绍了基于Expectile的VaR风险度量工具,并且提出半参数的CARE模型。半参CARE模型不仅无需对收益分布进行假设,而且采用Expectile回归方法刻画VaR,对信息利用更加充分。本文给出了半参数CARE模型的四种基本形式,对模型估计和检验做了详细说明。以中国股票市场的上证综指和深圳成指为研究对象,分别采用半参CARE模型和GARCH模型对两类指数2003年1月2日到2015年12月31日的VaR进行刻画。结果表明,AS-CARE模型能较好地刻画深圳成指5%VaR的变动情况,SAV-CARE模型能较好地刻画上证综指1%VaR的变动情况,GARCH-SKEWt模型能较好地刻画深圳成指1%VaR的变动情况,GARCH-t能较好地刻画上证综指5%VaR的变动情况。这说明,半参数CARE模型在度量中国股市风险时具有一定优势,能够作为中国股市风险度量工具的一个有益补充。
