极点与极线视角下的高考圆锥曲线试题

广东省东莞中学(523005) 于 涛

近年来,不少高考解析几何试题以极点、极线为背景,堪称出现频率最高的背景知识.文[1]介绍了极点与极线的概念及基本性质,笔者进行了进一步研究,证明了若干与圆锥曲线极点、极线有关的性质,与读者分享.

1.极点与极线的定义

定义1 (几何定义)如图1,P是不在圆锥曲线上的点,过点P引两条割线依次交圆锥曲线于四点E,F,G,H,连接EH,FG交于点N,连接EG,FH交于点M,则直线MN为点P对应的极线.特别地,若P是圆锥曲线上的点,则过点P的切线即为极线.同理,直线PN为点M对应的极线,直线PM为点N对应的极线.MNP称为自极三角形(参见[1]).

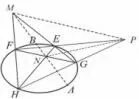
图1

如图1,由几何定义可知：(1)若连接MN交圆锥曲线于点A,B,则PA,PB恰为圆锥曲线的切线;(2)若点P与直线MN为圆锥曲线的一对极点与极线,记过极点P的两割线EF,GH与圆锥曲线的交点形成的四边形为EFHG,则极线MN与两对角线EH,FG三线共点.

定义2 (代数定义)已知圆锥曲线Γ∶Ax2+Cy2+2Dx+2Ey+F=0,则称点P(x0,y0)和直线l∶Ax0x+Cy0y+D(x+x0)+E(y+y0)+F=0 是圆锥曲线Γ 的一对极点与极线.[1]

具体地,明确曲线方程时,极点与对应的极线方程见下表：

曲线类型极点极线x2 a2+ y2 b2=1(x0,y0)x0x a2+ y0y b2=1(m,0)x= a2 m(m0)(0,t)y= b2 t (t0)x2 a2-y2 b2=1(x0,y0)x0x a2-y0y b2=1(m,0)x= a2 m(m0)(0,t)y=-b2 t (t0)y2=2px(x0,y0)y0y= p(x+x0)(m,0)x=-m

通过上表发现：特别地,当极点在圆锥曲线的对称轴上时,对应的极线垂直于该对称轴.

2.极点与极线的基本性质

性质1 如图2,已知点Q、直线l和圆锥曲线Γ,过Q作任意一条割线交Γ 于点A,B,交l于点P.若点Q与直线l是Γ 的一对极点与极线,则点P,Q调和分割线段AB,即也称点P,Q关于Γ 调和共轭.

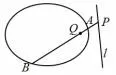
图2

图3

证明如图3,过极点Q作圆锥曲线Γ 的割线CD交极线l于点M,连接DA,BC交于点E,连接CA,BD交于点F,由极点与极线的几何定义知直线EF是极点Q对应的极线,故E,P,F,M四点共线.在△EBF中,因为ED,CF,BP三线共点A,由赛瓦定理得因为直线CDM截△EBF,由梅涅劳斯定理得所以即点M,P调和分割线段FE.连接BM,以点B为射影点,由交比定理得M,Q调和分割线段DC.连接EQ,以点E为射影点,由交比定理得P,Q调和分割线段AB,即

性质2 如图4,已知点P,Q和有心圆锥曲线Γ,直线PQ经过Γ 的中心O,与Γ 交于点R,R′(点R在P,Q之间).若P,Q关于Γ 调和共轭,则OP ·OQ=OR2.

性质3 如图5,已知点P,Q和圆锥曲线Γ(Q在Γ 内,P在Γ 外),直线PQ与Γ 交于点A,B(点A在P,Q之间).若P,Q关于Γ 调和共轭,则有(1)

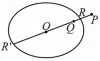
图4

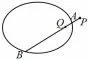
图5

性质2、3 的证明可应用性质1.

3.极点与极线的衍生性质

性质4 如图6、7,已知点P,Q在圆锥曲线Γ 的对称轴l上,过Q作直线交Γ 于点M,N.若P,Q关于Γ 调和共轭,则直线PM,PN与对称轴l所成的角相等.

图6

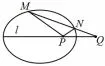
图7

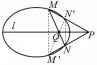
图8

证明当MN与l垂直时,命题显然成立; 当MN与l不垂直时,如图8,因为Γ 关于直线l对称,所以Γ 上存在M,N关于l的对称点M′,N′,易知MN.M′N′与l交于点Q,设MN′.M′N与l交于点P′,由几何定义知点P′,Q关于Γ 调和共轭,因为P,Q关于Γ 调和共轭,且点P在l上,所以P′与P重合,故直线PM,PN与对称轴l所成的角相等.

性质4 的逆命题也成立,证明过程略.

性质5 如图9、10,已知点Q在圆锥曲线Γ 的对称轴上,直线l垂直于该对称轴,过Q作直线交Γ 于点M,N,P为l上任意一点.若点Q与直线l是Γ 的一对极点与极线：

(1)如图9,当对称轴是x轴或平行于x轴时,kP M+kP N=2kP Q;

(2)如图10,当对称轴是y轴或平行于y轴时,

图9

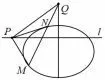
图10

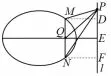
图11

图12

证明(1)如图11、12,分别过点M,N作l的垂线,垂足为点D,F,记l与对称轴的垂足为E.当MN与l平行时,如图11,kP M=易知MD=NF=QE,PD+PF=2PE,所以kP M+kP N=2kP Q;当MN与l不平行时,如图12,延长NM交直线l于点R,设直线NM的倾斜角为α,则所以由性质3 得2kP Q=连接EM,EN,由性质4 得△EMD～△ENF,所以又由MD//NF得两式相除得即整理得所以kP M+kP N=2kP Q.

(2)如图10,设PM,PQ,PN的倾斜角分别为β,γ,θ,则kP M=tanβ,kP Q=tanγ,kP N=tanθ,顺时针旋转90°,由性质5(1)得tan(β-90°)+tan(θ+90°)=2 tan(γ+90°),化简得所以

性质6 如图13、14,已知点Q、直线l和圆锥曲线Γ,过Q作直线交Γ 于点M,N,在直线l上任取一点P,连接PQ,分别过M,N作PQ的平行线交l于点S,T.若点Q与直线l是Γ 的一对极点与极线,则S2△MP N=4S△MP SS△NP T,或S2△SQT=4S△MQSS△NQT.

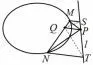
图13

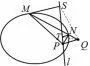
图14

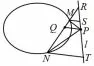
图15

证明如图15,延长NM交直线l于点R,设直线NM与直线PQ所成的角为α,则S△MP S=MS ·MQsinα,由性质3 得两式相乘得由 性质1 得MR · NQ=NR · MQ,所 以即

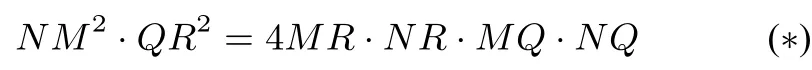
又因为MS//QP//NT,所以代入(∗)式 得NM2· QP2=4MS · NT · MQ · NQ,所以S2△MP N=4S△MP SS△NP T.由S△SQT=S△MP N,S△MQS=S△MP S,S△NQT=S△NP T,得S2△SQT=4S△MQSS△NQT.

性质4、5、6 的证明只证明了一种情形,其它情形证明过程类似,不再赘述.

4.极点与极线知识的应用

例1 (2016年全国I卷文科第20题)在直角坐标系xOy中,直线l∶y=t(0)交y轴于点M,交抛物线C∶y2=2px(p＞0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.

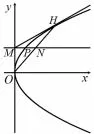
图16

简析(I)略; (II)如图16,由(I)得,M(0,t),lON∶y=即ty=px,由代数定义知点M与直线lON是抛物线C的一对极点与极线,又因为lON与曲线C交于点O,H,由几何定义得MO,MH均为抛物线C的切线,所以除H以外,直线MH与C没有其它公共点.

例2 (2012年高考北京卷理科第19 题)已知曲线C∶(5-m)x2+(m-2)y2=8(m ∈R).

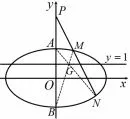
图17

(I)若曲线C是焦点在x轴上的椭圆,求m的取值范围;

(II)设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4 与曲线C交于不同的两点M,N,直线y=1 与直线BM交于点G.求证：A,G,N三点共线.

简析(I)略; (II)m=4 时,曲线C为椭圆1,如图17,因为直线y=kx+4 恒过定点P(0,4),由代数定义知点P与直线y=1 是椭圆C的一对极点与极线,直线MN和AB为过极点P的两割线,由几何定义知极线y=1与四边形ABNM的对角线三线共点,因为极线y=1 与对角线BM交于点G,所以点G在另一条对角线AN上,即A,G,N三点共线.

例3 (2007年高考福建卷理科第20 题)已知点F(1,0),直线l∶x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且

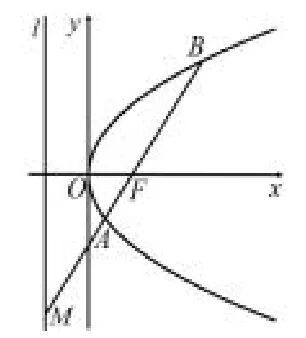
图18

(I)求动点P的轨迹C的方程;

(II)过点F的直线交轨迹C于A,B两点,交直线l于点M,已知求λ1+λ2的值.

简析(I)C∶y2=4x; (II)如图18,由(I)知点F与直线l是抛物线C的一对极点与极线,由性质1得则故λ1=λ,λ2=-λ,所以λ1+λ2=0.

图19

例4 (2015年高考北京卷理科第19 题)已知椭圆C∶的离心率为点P(0,1)和 点A(m,n)(0)都在椭圆C上,直线PA交x轴于点M.

(I)求椭圆C的方程,并求点M的坐标(用m,n表示);

(II)设O为原点,点B与点A关于x轴对称,直线PB交x轴于点N.问：y轴上是否存在点Q,使得∠OQM=∠ONQ? 若存在,求出点Q的坐标;若不存在,说明理由.

简析(I)C∶(II)如图19,由∠OQM=∠ONQ,∠QOM=∠NOQ,得△OQM～△ONQ,故|OQ|2=|ON|·|OM|.由几何定义知点N是点M对应极线上的一点,即点M,N关于椭圆C调和共轭,又因为椭圆C的中心O在直线MN上,记椭圆C的右顶点为D,由性质2 得|ON|·|OM|=|OD|2=2,故|OQ|2=2,所以Q的坐标为

例5 (2015年全国I 卷理科第20 题)在直角坐标系xOy中,曲线C∶y=与直线l∶y=kx+a(a＞0)交于M,N两点.

(I)当k=0 时,分别求C在点M和N处的切线方程;

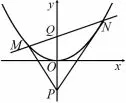
图20

(II)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN? 说明理由.

简析(I)略; (II)如图20,由题得抛物线C的对称轴为y轴,直线l恒过y轴上点Q(0,a),因为∠OPM=∠OPN,且点P在y轴上,由性质4 的逆命题得P,Q关于抛物线C调和共轭,由代数定义得点P的坐标为(0,-a).

例6 (2013年高考江西卷文科第20 题)椭圆C∶=1(a＞b＞0)的离心率e=a+b=3.

(I)求椭圆C的方程;

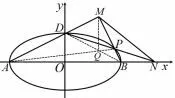
图21

(II)如 图21,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M,设BP的斜率为k,MN的斜率为m.证明：2m-k为定值.

简析(I)(II)如图21,连接AP,BD交于点Q,连接MQ,由几何定义知点N与直线MQ是椭圆C的一对极点与极线,由性质5 得kMP+kMD=2kMN,即k+kMD=2m,因为kMD=kAD=所以k-2m=

例7 (2009年高考湖北卷理科第21题)过抛物线y2=2px(p＞0)的对称轴上一点A(a,0)(a＞0)的直线与抛物线相交于M,N两点,自M,N向直线l∶x=-a作垂线,垂足分别为M1,N1.

图22

(II)记△AMM1,△AM1N1,△ANN1的面积分别为S1,S2,S3,是否存在λ,使得对任意的a＞0,都有S22=λS1S3成立? 若存在,求出λ的值,否则说明理由.

简析(I)略; (II)如图22,由代数定义知点A与直线l是抛物线y2=2px(p＞0)的一对极点与极线,由性质6 得S22=4S1S3,故λ=4.

以极点、极线为背景的高考解析几何试题还有很多,例如,2018年全国I 卷文、理解析几何解答题就是以性质4 为背景的试题.通过列举的7 道真题,不难体会极点与极线知识内容的丰富性,虽然极点与极线的知识不属于高考考查内容,但是了解极点与极线的相关知识,能帮助教师和学生打开思维视角,培养学生探究数学问题的能力.