一种基于自适应轮廓波变换的图像编码方法

2019-04-12徐庆红方力钟微蒋克华

中国传媒大学学报(自然科学版) 2019年1期

徐庆红，方力，钟微，蒋克华

(中国传媒大学媒介音视频教育部重点实验室，北京 100024)

1 引言

随着社交媒体的发展，近几年网络上的图像数量呈爆炸性增长。为了有效地传输和存储图像，有必要研究高效的图像压缩方法。图像压缩编码过程中的稀疏变换环节十分重要，通过变换可以把空间域的大量图像数据转换到变换域，用很少的数据来表示原始图像，以达到“稀疏”表示原图像的目的。常用的变换有傅立叶变换、离散余弦变换、小波变换等，其中小波变换更是被新一代图像压缩标准 JPEG2000[1]所采用。然而，可分离的二维小波来自一维小波的张量积，其基函数具有各向同性，因此只能表示图像信息竖直、水平和对角线方向的直线奇异性。而自然图像作为一种具有高维奇异曲线或曲面的特殊信号，二维小波逼近图像中的奇异曲线时，随着小波基尺度不断变细，非零小波系数会以指数的形式不断增长，重要不可忽视系数大幅增加，最终变为用“点”来逼近曲线。因此，小波变换并不能为高维奇异图像提供高效的或者最稀疏的表示。

在这种背景之下，图像的“多尺度几何分析(multiscale geometric analysis，MGA)”[2]理论被提出来。多尺度几何分析是一种数学分析工具，不仅具有小波变换的多分辨率特性、时频局部性，而且还具有多方向性和各向异性。多尺度几何分析能够对高维奇异图像进行稀疏展开，使变换具有更强的非线性逼近能力，弥补了小波变换在处理高维奇异图像过程中的不足。常见的多尺度几何分析工具中，脊波变换[3]首先利用Radon变换把图像的线奇异映射为Radon域上的点奇异，然后再用小波变换处理点奇异频域图像。曲线波变换[4]是脊波变换的衍生，由滤波和多尺度脊波变换组成，其基本思想是先把图像的曲线奇异分割成平滑的直线奇异，然后再利用脊波变换处理局部的直线奇异，分解方法较复杂。轮廓波变换[5-6]继承了脊波和曲线波变换的优点，它通过多尺度和多方向滤波联合完成分解，分解过程中首先利用拉普拉斯金字塔滤波器完成多尺度分解，然后通过方向滤波器组实现多方向分解，其冗余度减少至33%。然而轮廓波变换不具备平移不变性，在信号去噪时会产生伪吉布斯现象。为了解决这个问题，Cunda等人[7]提出了非下采样的轮廓波变换。剪切小波是复合小波的延伸，具有多尺度框架和各向异性，在多变量问题中能高效率变换。Kutyniok 等人[8]对剪切小波做了系统的介绍，并应用到实际图像压缩编码中。然而，上述这些多尺度几何分析工具大都具有固定的子带划分策略，没有考虑输入图像信号的频率分布特性，由于自然图像包含了丰富复杂的纹理信息和几何轮廓信息，使用上述这些固定分解的方法无法实现高效稀疏表示。

针对上述问题，本文提出了一种基于熵准则的自适应轮廓波变换方法。该方法能够根据图像的频率分布特性，在子带香农能量熵的指导下，对图像进行自适应多尺度分解，并进一步对各个子带进行自适应方向分解，最终实现图像的高效稀疏表示。实验结果表明，使用该方法可以显著提高图像编码的质量。

论文剩余部分结构安排如下：第二节介绍了自适应变换的基本思想，提出了一种基于熵准则的自适应轮廓波变换；第三节提出了一种基于自适应轮廓波变换的图像编码方法，并进行实验分析；第四节给出了结论。

2 自适应轮廓波变换方法

2.1 自适应变换基本思想

自然图像包含丰富的纹理信息和边缘轮廓信息，不同图像内容差异很大，因此采用相同的分解策略难以获得高效的稀疏表示。而采用自适应方法，可以根据输入图像内容的不同，自适应地采用不同的分解策略，从而实现图像的高效稀疏表示。

香农能量熵(Shannon energy entropy)[9]是图像“繁忙”程度的估计值，对于M×N的图像信号，香农能量熵定义如下：

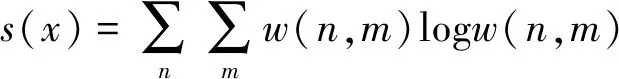
(1)

(2)

(3)

其中s(n，m)、w(n，m)、x(n，m)和p分别为图像的能量熵、图像中各像素功率在总功率中的比率、图像各个像素值和图像像素总功率。

对于熵值越高的图像(在亮度上有很多细节和变化，如有很多鹅卵石的地面，阴影对比分明)，将需要更高的压缩设置来满足最终的目标图像大小限制。对于熵值低的图像，比如飘着一些云彩的天空，没有太多的细节和变化，因而只要较少的压缩量就能满足目标图像大小限制。因此，我们采用如下的自适应子带划分策略：对于熵值较高的子带，通过进一步分解，来获得其更高效的稀疏表示；反之，对于熵值较低的子带，则不需要再进一步分解。

由于轮廓波变换采用了树型结构，非常符合上述由粗到细的分解策略，而且轮廓波相对于剪切波等变换冗余较小，更适用于图像编码。因此，我们把基于香农能量熵的自适应分解方法应用到轮廓波变换中，在轮廓波变换的多尺度分解和多方向分解过程中基于图像的频率分布对图像进行自适应子带划分，从而实现图像的高效稀疏表示。

2.2 自适应轮廓波变换

2.2.1 轮廓波变换

轮廓波变换的基函数与小波基函数不同。轮廓波变换的基函数的紧支集支撑区间为“长方形”，为了逼近奇异曲线，随着尺度的不断变化，长方形的长宽比发生变化，最终会变为用“线段”的形式逼近原函数，这也正是轮廓波变换的名称由来。如图1所示。

图1 轮廓波逼近曲线的过程

轮廓波变换的基本结构如图2所示。从组成结构来看，轮廓波变换是一种双重滤波器组结构[10]，其核心是拉普拉斯塔形方向滤波器组，它由拉普拉斯塔式滤波器[11]和方向滤波器组[12]两部分构成，分别完成信号的多尺度分解和多方向分解。

图2 轮廓波变换的结构

2.2.2 轮廓波自适应变换过程

虽然轮廓波变换的尺度分解和方向分解完全独立，但是都采用了由粗到细的分解模式。另外，尺度和方向分解的等级参数完全由执行者预先设置，没有考虑图像的频率分布。为了解决这个问题，我们借助基于熵准则的自适应分解，在尺度分解时根据低频子带系数的香农能量熵自适应确定分解级数，在多方向分解时根据方向子带系数的香农能量熵自适应确定方向子带的数目，从而实现图像的自适应分解。

自适应轮廓波分解包括以下两步：

1)多尺度分解：用拉普拉斯金字塔滤波器对原始图像进行低高通子带的分解，分别得到低通子带L1和高通子带H1，根据公式(2)计算低通子带L1的香农能量熵值S1，将低通香农能量熵值S1与阈值熵SL进行比较，香农能量熵S1大于阈值熵SL则继续进行二级尺度分解，同理对二级低通子带继续进行能量判决确定是否分解，以此类推，直到最后分解等级的低通子带能量熵值Si小于阈值熵值SL，则停止尺度分解。图3为拉普拉斯金字塔自适应分解流程图，其中i=1。

2)多方向分解：对拉普拉斯金字塔多尺度分解后的带通子带进行多方向滤波。多方向滤波器组对子带频率进行方向划分，一级方向分解把带通子带分解为左右两个方向子带树，计算左子树方向子带香农能量熵S11，能量熵S11与阈值熵SD进行判决，当S11>SD则继续进行二叉方向分解，对下一级方向分解使用同种判决分解方式，直到分解的方向子带不满足以上条件为止；对右子树判决分解方式与左子树分解一样，阈值熵SD大小不变，方向分解直到最后的方向子带能量熵不满足条件为止。左右子树分解完成，最终实现自适应多方向滤波。图4为自适应多方向分解框架，其中i=1。

图像重构是图像分解的逆过程。自适应轮廓波重构包括以下两步：

1)方向子带重构。将分解得到的方向子带系数进行反变换，得到i尺度下的带通子带高频系数fi。

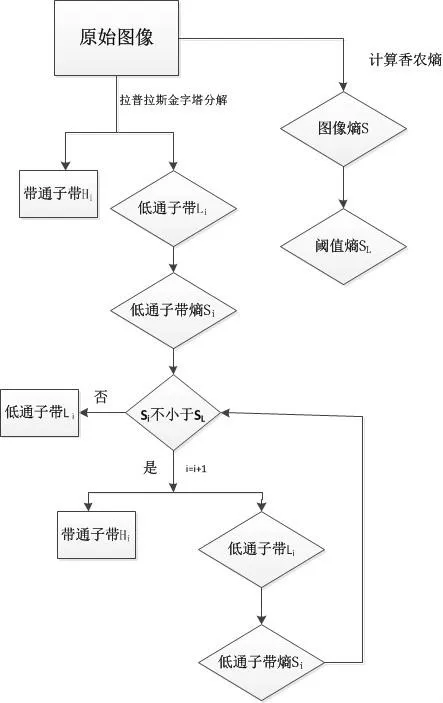
图3 拉普拉斯金字塔自适应分解

图4 多方向自适应滤波

3 实验与分析

依据图像编码框架，本文提出一种基于最小熵自适应轮廓波变换的图像编码算法。编码结构采用JPEG2000的基本框架，自适应轮廓波变换代替小波变换。编码结构如图5所示。

图5 自适应轮廓波变换编码框架

编码过程中，首先利用自适应变换对图像进行尺度和方向的分解；然后对所得变换系数进行量化，考虑到不同尺度下变换系数的能量分布不同，所以对不同子带采用不同的量化步长；最后不同尺度分等级进行编码，实现图像的编码过程，详细流程如下：

(1)由公式(1)计算原始图像的香农能量熵s(n，m)，根据原始图像的香农能量熵值大小，分别设定多尺度分解和多方向分解的阈值SL和SD，SL=γL×s(n，m)，SD=γD×s(n，m)，(其中γL、γD分别为多尺度变换和多方向变换的阈值系数)对原始图像进行自适应轮廓波分解，得到变换系数；

(2)对变换后的各子带系数根据父子关系进行重排，记录子带系数分布以及大小关系；

(3)同一子带均匀量化，不同子带根据子带特性采用不同量化阈值。子带系数量化，得到二进制符号流；

(4)对二进制符号流进行算术编码，最终输出压缩后的比特流。

实验采用大小为512×512像素的“man”、“lena”和256×256像素的“object”灰度图像作为测试图。通过对大量图像的测试分析，多尺度变换和多方向变换阈值系数γL和γD分别设定为1%和4%。我们将本文提出的编码方法与基于脊波、曲线波、轮廓波等变换的编码方法的结果进行比较，表1给出不同码率下的PSNR值；图6、7给出不同编码方法在不同图像下的PSNR曲线。

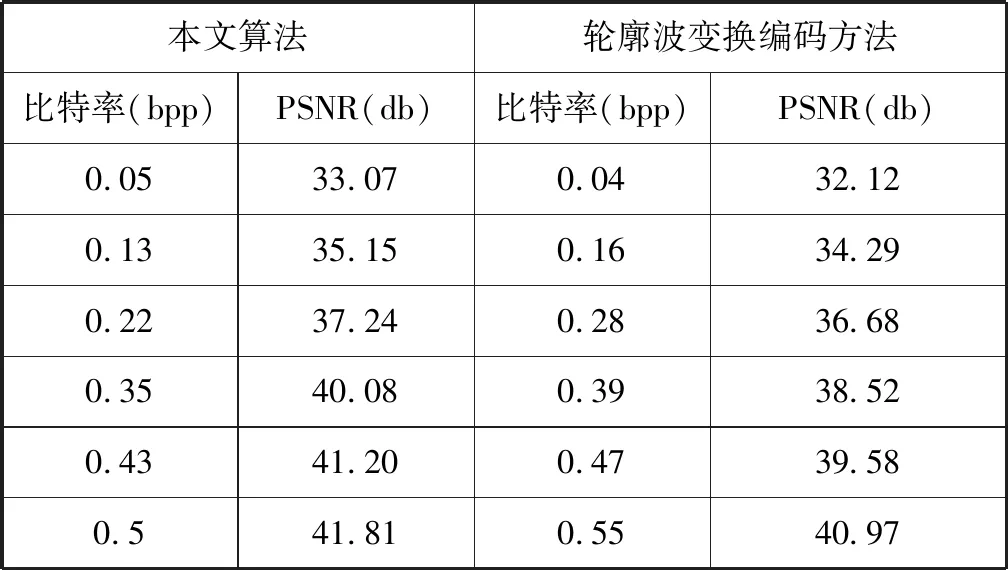
表1 Man

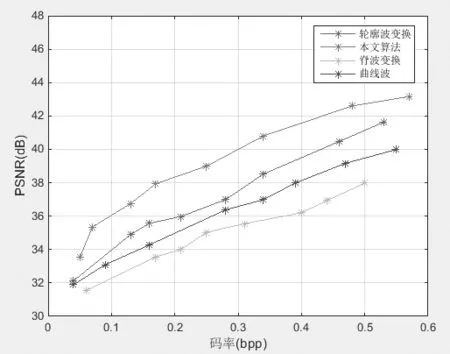
图6 “lena”图像采用不同编码方法的PSNR比较

图7 “object”图像采用不同编码方法的PSNR比较

从表1和图6、7中可以看出，在所有测试图像中，本文提出的编码算法与轮廓波变换编码算法相比在编码性能上均有所提升，提升约0.5-2db，其对轮廓比较复杂的图像效果尤其好。

图8、9所示为测试图“man”、“lena”采用轮廓波变换和本文方法的重构效果图。图8为当码率为0.16bpp时，两种方法下“man”a、b重构图；图9为码率为0.07bpp时，两种方法下重构lena的部分展示图像c、d。

从图8、9中可以看出采用自适应轮廓波变换编码方案重构后的图像整体轮廓清晰，而轮廓波变换编码重构后的图像中纹路模糊，视觉效果下降。因此，采用本文算法同码率下重构图像的主观视觉质量有所提升。

4 结论

本文提出了一种适用于图像稀疏表示的基于熵准则的自适应轮廓波变换方法，可以根据图像频率分布特性，实现尺度和方向由粗到细的自适应分解。我们将该变换应用于JPEG2000编码框架，实现图像的压缩编码。实验结果表明本文所提编码方法在图像编码中，能够很好的提取图像的轮廓纹理信息，与基于脊波、曲线波、轮廓波等变换的编码方法相比，同等码率下峰值信噪比提升约0.5-2 dB。