认知型水声通信时空自适应处理算法研究

王峰，周易，龚道银



认知型水声通信时空自适应处理算法研究

王峰1,2，周易1，龚道银1

(1. 河海大学计算机与信息学院，阵列与信息处理实验室，江苏南京 211100； 2.厦门大学水声通信与海洋信息技术教育部重点实验室，福建厦门 361005)

针对浅海水声通信面临的复杂干扰环境，提出了一种适用于水声通信系统的认知型时空自适应处理算法。该算法在传统时空自适应阵列处理算法的基础上引入了干扰认知的功能，通过干扰认知处理降低计算量，并且实现干扰样本的选取，确保自适应算法的可靠收敛。利用了协方差矩阵特征分解和多重信号分类(Multiple Signal Classification, MUSIC)估计干扰的个数，辅助选取盲源分离算法中的维度和时空自适应算法中的空域维度，进行算法降维处理。针对采用盲源分离后的各干扰，采用包络检测法提取时域特征，采用短时傅里叶变换(Short-time Fourier Transform, STFT)方法提取时频谱特征，分析干扰特征，实现干扰分类，从而实现干扰样本的选取。通过计算机仿真验证了该认知处理算法的性能。

认知水声通信；时空自适应处理；特征提取

0 引言

由于电磁波在水中衰减严重，传输距离受限，水声通信技术成为海洋开发探索和潜艇通信的重要手段[1-2]。浅海水声通信面临着来自多方面的干扰，相对于通信目标的其它用户干扰、航线船只与风暴造成的连续波干扰、海洋生物鸣叫和人类在海洋中的施工造成的脉冲干扰[3]，极大地降低了水声通信系统的性能。

目前已有多篇文献针对水声通信干扰进行了研究。文献[3]提出了一种基于稀疏贝叶斯学习的脉冲噪声估计算法，利用接收端频域信号和后验概率估计脉冲噪声。文献[4]采用门限消除方法对脉冲干扰进行了抑制。但是上述文献只能检测出脉冲这一种干扰。在文献[5]中，使用基于最小均方算法(Least Mean Square, LMS)算法的锁相环-判决反馈均衡器结构，提高均衡器跟踪信道变化的能力，抑制强多径干扰，但是有些干扰不能直接采用LMS算法进行处理，例如脉冲干扰，自适应算法收敛受到脉冲干扰出现位置的影响，抑制难度较大。

针对以上算法的不足，本文提出了一种基于认知的水声通信时空自适应处理算法。该算法在传统的时空自适应干扰抑制算法的基础上，引入了协方差矩阵特征分解、MUSIC空间谱估计、包络特征提取和短时傅里叶变换(Short-time Fourier Transform, STFT)等算法，实现时空自适应算法的降维处理和对消样本选取。

1 认知型水声通信时空自适应处理算法

1.1 传统的时空自适应算法原理[6-10]

基于线性约束最小方差(Linearly Constrained Minimum Variance, LCMV)准则，最佳权向量使用式(3)求解：

其中：

1.2 认知型时空自适应阵列处理

认知型时空自适应处理原理框图如图1所示。该算法是在传统时空自适应阵列处理算法的基础上引入了基于干扰特征分析的干扰认知功能。干扰认知计算阵列接收信号的协方差矩阵，进行特征分解和MUSIC空间谱估计，计算干扰个数。干扰个数主有两个方面的应用：一是辅助选取盲源分离算法中的维度，从而有效降低通道数量，降低算法的复杂度；二是辅助选取时空自适应算法中的空域维度，进行算法降维处理，从而降低时空自适应处理算法的计算量。采用基于快速独立分量分析(Fast Independent Component Analysis, Fast-ICA)的盲源分离算法将干扰分离开后，采用包络检测方法分析时域特征，采用STFT分析时频谱，从而提取干扰特征，识别干扰类型。最后根据干扰类型选取合适的干扰样本进行时空自适应抵消，提高自适应算法的收敛速度。

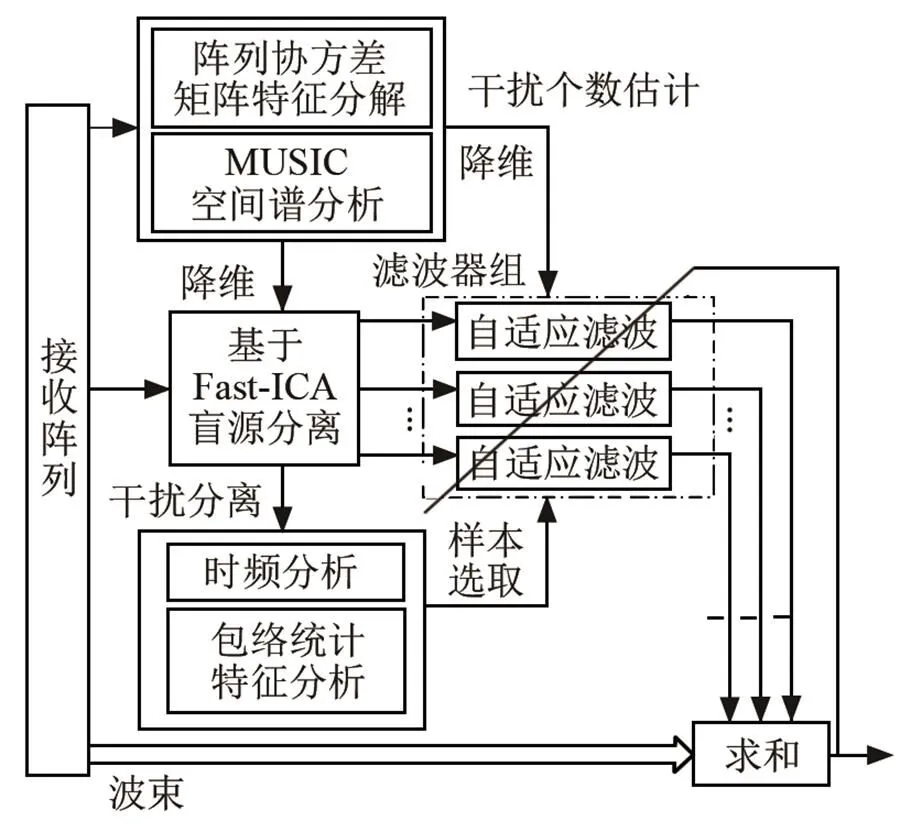
图1 认知型空时自适应处理原理框图

水声通信常见的干扰形式主要为噪声调频干扰、脉冲干扰以及线性扫频干扰等，噪声调频干扰具有带宽较宽、功率谱均匀和干扰功率大的特点；脉冲干扰具有持续时间短、瞬时功率大、信号幅度因大瞬时功率的影响可能出现饱和或限幅的特点；线性扫频干扰具有频率特征成线性的特点。本文针对噪声调频干扰、脉冲干扰和线性扫频干扰这三种干扰，按图1所示框图，对接收阵列做了如下处理：

(1) 干扰源个数估计

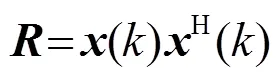
然后对协方差矩阵进行特征值分解：

(2) 干扰方向估计

MUSIC方法利用了信号子空间和噪声子空间的正交性，构造空间谱函数。通过谱峰搜索，检测出水声通信中干扰的方向，公式为[12]

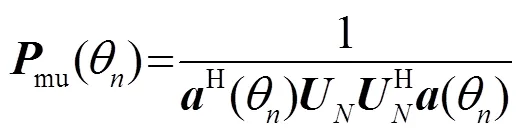
(3) 干扰分离

基于负熵最大的FastICA算法的基本步骤如下[13-14]：

步骤1：对观测信号矩阵进行预处理，包括去均值和白化，得到预白化信号；

步骤4：每次迭代提取一个新的独立成份时，为避免迭代的新权与已经求出的权值向量收敛到相同方向，需进行去相关处理，即正交化投影操作，公式如下：

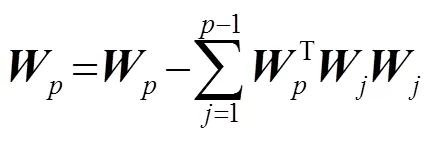
步骤5：归一化处理，公式如下：

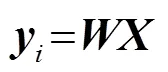
(4) 频谱占用分析

使用快速傅里叶变换(Fast Fourier Transform, FFT)对盲源分离后的各干扰进行频谱占用分析，从而提取带宽特征。具体步骤如下：①提取FFT后频谱幅度的最大值；②以最大值的0.707倍为门限，计算超出该门限的频谱宽度，作为干扰的带宽。噪声调频干扰和脉冲干扰的带宽较宽，覆盖整个工作频带，而线性扫频干扰的带宽较小。

(5) 时域包络特征提取

针对盲源分离后的各种干扰信号，提取脉宽和占空比特征，判断干扰是连续波还是脉冲。

①脉宽

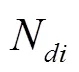
②占空比

占空比是指整个样本中脉冲所占的比例，计算公式为

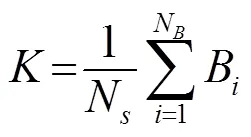
(6) 时频谱特征提取

STFT对时频特征的提取非常有效，对于扫频干扰和噪声调频干扰等存在明显时频谱特征的信号，可以采用提取相应时延峰值的方法实现特征判断。因此，采用STFT测量干扰的时频特征，时频谱特征分析原理框图如图2所示。

图2 时频谱特征分析原理框图

盲源分离后，对各干扰信号分别做STFT并进一步提取峰值一阶差分的方差特征，然后根据特征值的不同进行门限判决，识别出相应的干扰类型。

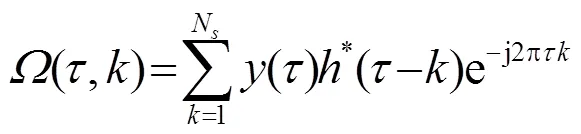
综上所述，获取干扰特征后对干扰进行认知，如果根据包络特征判定为脉冲干扰，根据STFT判定为非线性扫频干扰，则最终判定为脉冲干扰。如果根据包络特征判定为连续波干扰，根据STFT判定为线性扫频干扰，则最终判为线性扫频干扰。如果根据包络特征判定为连续波干扰，根据STFT判定为非线性扫频干扰，则最终判为噪声调频干扰。识别水声干扰类型后，根据干扰类型选取自适应干扰抵消的样本，通过时空自适应算法抑制干扰。

2 算法性能仿真

2.1 仿真1：干扰认知仿真

使用基于负熵最大的Fast-ICA迭代算法实现干扰信号的分离，分离结果如图5所示。

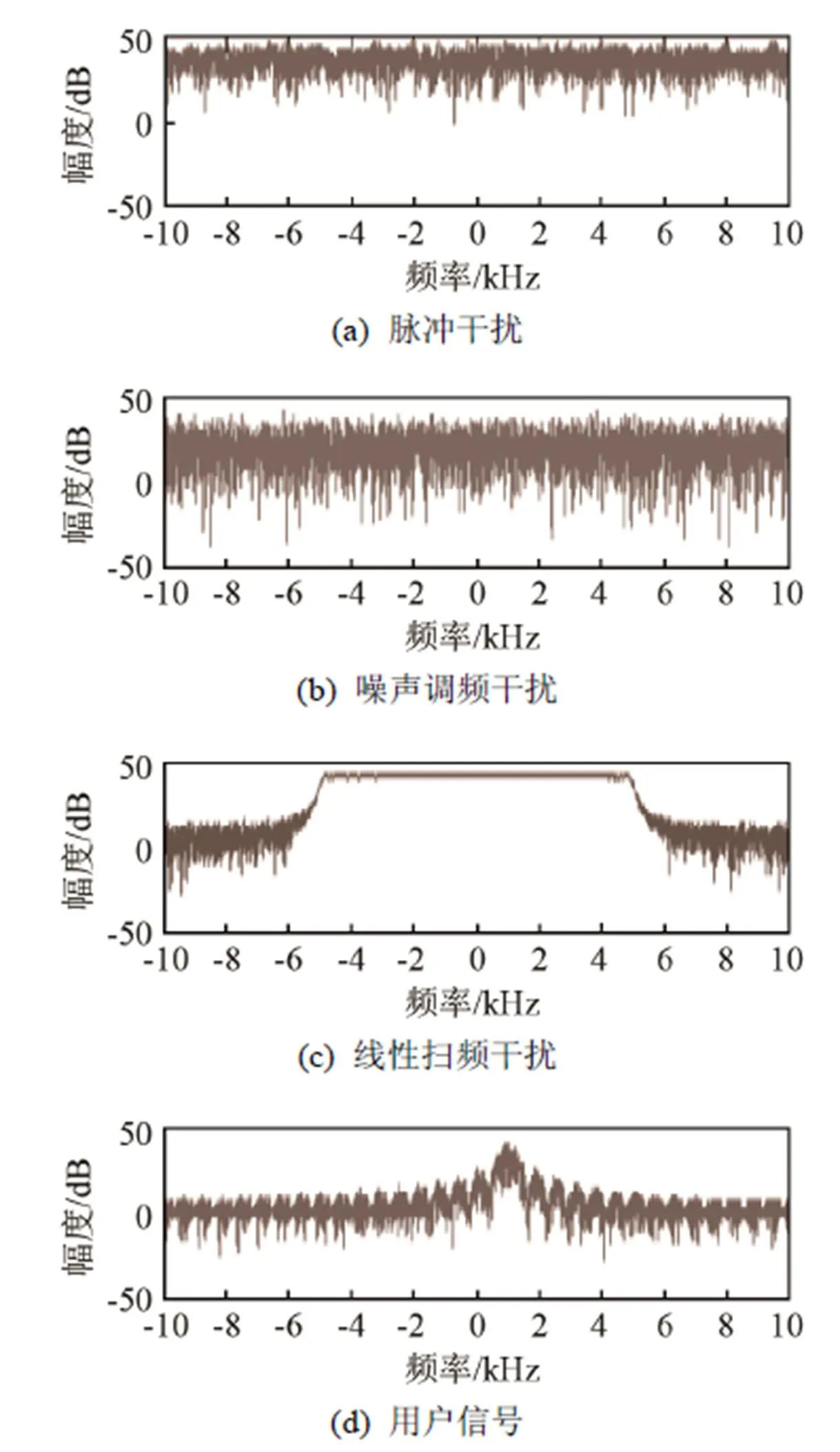
图3 干扰信号与用户信号的频带占用图

图4 MUSIC空间谱测向

对分离后的三种干扰信号分别提取包络特征，干扰1的脉宽为80个采样点，占空比为0.22；干扰2的脉宽为4 000个采样点，占空比为1；干扰3的脉宽为4 000个采样点，占空比为1。

采用STFT处理后的干扰信号时频图如图6所示。提取时频谱的频率峰值，计算三种干扰峰值的一阶差分的方差，分别为4 747、6 723、0.15。

综上所述，仿真中提取的干扰特征参数如表1所示。

根据上述提取的特征，干扰1脉宽为80采样点，小于脉宽门限值500采样点；占空比为0.22，小于占空比门限0.7，所以干扰1最终判为脉冲干扰。干扰2占空比为1，大于占空比门限0.7，判为连续波干扰；频率峰值一阶差分的方差为6 723，远大于差分方差门限1，所以干扰2最终判为噪声调频干扰。干扰3的占空比为1，大于占空比门限0.7，判为连续波干扰；频率峰值一阶差分的方差为0.15，小于差分方差门限1，所以干扰3最终判为线性扫频干扰。干扰个数、方向和种类均与仿真条件设置一致，验证了认知干扰算法的有效性。

图5 盲源分离后干扰信号时域图

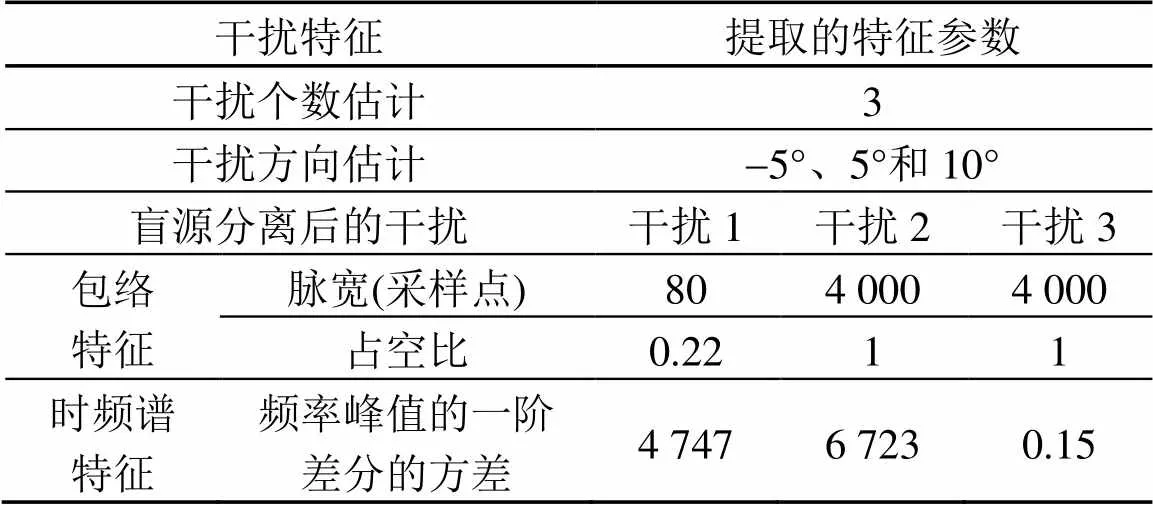
表1 干扰特征参数

仿真通道中的信噪比保持-20 dB不变，改变干噪比，每种干噪比下改变脉冲干扰的脉宽、线性扫频干扰的带宽和噪声调频干扰的频率等参数，按照图1的流程框图对干扰进行分类，每种干噪比的蒙特卡洛仿真次数为300，分类正确率如图7所示。

由图7中可见，干噪比高于8 dB时，本算法可以获得较高的识别率，正确率可达99%以上。

图7 不同干噪比下的干扰分类正确率

2.2 仿真2：时空自适应处理仿真

识别干扰类型后选取样本，再采用时空自适应算法对干扰进行抑制，例如脉冲干扰，选取脉冲干扰出现的样本。本仿真中有三个干扰，选取三个辅助通道。仿真1中干扰抑制前后的功率如图8所示，抵消比为16.82 dB。抑制前后相干图如图9所示，由图9可见，抑制前后相关峰值相同，抵消后旁瓣被压低，证明了抵消后得到的结果是用户信号，验证了抑制算法的有效性。

图8 干扰抑制前后功率图

图9 抵消前后相关图

3 结论

本文结合水声通信干扰特征认知和空时自适应处理算法，通过对干扰个数的认知，降低了盲源分离算法和空时自适应算法中的计算量，通过对时域包络和时频谱的多特征融合认知，实现了噪声调频干扰、脉冲干扰和线性扫频干扰的分类识别，完成了干扰样本的选取，最终保证了时空自适应处理的可靠收敛。计算机仿真验证了该方法的有效性。

[1] 贾宁, 黄建纯. 水声通信技术综述[J]. 物理, 2014, 43(10): 650-657.

JIA Ning, HUANG Jianchun. An overview of underwater acoustic communications[J]. Physics, 2014, 43(10): 650-657.

[2] 王峰, 刘蝶. 认知型宽带恒模阵列水声通信多用户信号分离与干扰抑制算法[J]. 数据采集与处理, 2017, 32(6): 1089-1096.

WANG Feng, LIU Die. Source separation and jamming suppression for underwater acoustic communication systems with cognitive capability[J]. Journal of Data Acquisition and Processing, 2017, 32(6): 1089-1096.

[3] 李程程, 李有明, 吕新荣, 等. 水声通信中脉冲干扰和载波频偏联合估计算法的研究[J]. 信号处理, 2015, 31(11): 1473-1478.

LI Chengcheng, LI Youming, LYU Xinrong, et al. Joint impulsive noise and carrier frequency shift estimation in underwater acoustic communication[J]. Journal of Signal Processing, 2015, 31(11): 1473-1478.

[4] XU X, ZHOU S, SUN H, et al. Impulsive noise suppression in per-survivor processing based DSSS systems[C]//Oceans IEEE(S0197-7385), 2015: 1-5.

[5] 李记龙, 冯海泓, 黄敏燕. 强多径干扰下的水声通信均衡算法研究[J]. 声学技术, 2016, 35(1): 73-77.

LI Jilong, FENG Haihong, HUANG Minyan. Study of channel equalization of underwater acoustic communication in muitipath horizontal channel[J]. Technical Acoustics, 2016, 35(1): 73-77.

[6] 于永, 雷志勇. 基于STAP杂波抑制的子阵优化技术[J]. 现代雷达, 2016, 38(9): 28-31.

YU Yong, LEI Zhiyong. Optimization technology of subarray division based on STAP clutter suppression[J]. Modern Radar, 2016, 38(9): 28-31.

[7] RUI F, LAMARE R C D. Reduced-rank STAP algorithms using joint iterative optimization of filters[J]. IEEE Transactions on Aerospace & Electronic Systems (S0018-9251), 2011, 47(3): 1668 -1684.

[8] ABDELKAREEM A E, SHARIF B S, TSIMENIDIS C C. Adaptive time varying doppler shift compensation algorithm for OFDM-based underwater acoustic communication systems[M]. Nortn-Holland: Elsevier Science Publishers, B. V. 2016.

[9] PALMER J E, SEARLE S J. Evaluation of adaptive filter algorithms for clutter cancellation in Passive Bistatic Radar[C]//IEEE Radar Conference. IEEE(S2375-5318), 2012: 493-498.

[10] MA Y, SHAN T, ZHANG Y D, et al. A novel two-dimensional sparse-weight NLMS filtering scheme for passive bistatic radar[J]. IEEE Geoscience & Remote Sensing Letters(S1545-598X), 2016, 13(5): 676-680.

[11] AUBRY A, MAIO A D, PALLOTTA L. A geometric approach to covariance matrix estimation and its applications to radar problems[J]. IEEE Transactions on Signal Processing(S1053-587X), 2018, 66(4): 907-922.

[12] 杜梓冰, 杨坤德. 低信噪比下重构协方差矩阵的高分辨MUSIC算法[J]. 声学技术, 2013, 32(5): 373-378.

DU Zibing, YANG Kunde. High resolution MUSIC algorithm reconstructing covariance matrix in low SNR[J]. Technical Acoustics, 2013, 32(5): 373-378.

[13] DERMOUNE A, WEI T. FastICA algorithm: five criteria for the optimal choice of the nonlinearity function[J]. IEEE Transactions on Signal Processing(S1053-587X), 2013, 61(8): 2078-2087.

[14] 何安玲, 何选森. 基于有理非线性函数的Fast-ICA算法[J]. 计算机工程与应用, 2018(1): 251-255.

HE Anling, HE Xuansen. Improved Fast-ICA algorithms with rational nonlinearities[J]. Computer Engineering and Applications, 2018(1): 251-255.

[15] PEI S C, HUANG S G. STFT with adaptive window width based on the chirp rate[J]. IEEE Transactions on Signal Processing(S1053-587X), 2012, 60(8): 4065-4080.

Space-time adaptive processing with cognitive capability for underwater acoustic communication systems

WANG Feng1,2, ZHOU Yi1, GONG Dao-yin1

(1.Array and Information Processing Laboratory, College of Computer and Information, Hohai University, Nanjing 211100, Jiangsu, China; 2. Key Laboratory of Underwater Acoustic Communication and Ocean Information Technology of Ministry of Education, Xiamen University, Xiamen 361005, Fujian, China)

In order to mitigate the jamming effect in underwater acoustic communication system, a cognitive space-time adaptive processing algorithm is proposed, which converges faster and reliably due to the sample selection based on interference cognition. The number of jamming is estimated by covariance matrix feature decomposition and MUSIC power spectrum, and the algorithm dimensionality reduction processing is carried out based on the auxiliary selection of the dimensions of the blind source separation algorithm and the spatial dimension of the space-time adaptive algorithm. For the interference after blind source separation, several interference cognition methods exploited to sample selection are studied, including the time domain analysis based on envelope detection and the time-frequency analysis based on Short-time Fourier Transform (STFT). Finally, the performance of this algorithm is confirmed by numerical simulations.

cognitive underwater acoustic communication;space-time adaptive processing; characteristic extraction

O427

A

1000-3630(2019)-01-0091-06

10.16300/j.cnki.1000-3630.2019.01.015

2018-05-04;

2018-07-18

水声通信与海洋信息技术教育部重点实验室开放基金资助(厦门大学)(201703)，江苏省自然科学基金资助项目(BK20151501)，中央高校基本科研业务费专项资助项目(2015B03014)。

王峰(1976－), 男, 山东淄博人, 博士, 硕士生导师, 教授, 研究方向为水声通信技术，智能电子战技术。

周易,E-mail: zhouyi_free@163.com