基于VMD-SWT滚动轴承故障诊断方法研究＊

周进群，刘义亚

（1.深南电路股份有限公司，深圳 518000；2.无锡深南电路股份有限公司，江苏 无锡 214000）

前言

随着社会的不断发展进步，工业设备日渐趋于智能化、大型化，这就给故障诊断领域提出了严峻的挑战。滚动轴承在所有机械设备中占据着举足亲重的地位，是机械设备中最重要的结构之一，一旦损坏，轻则导致巨大的经济损失，重则危及人生安全战[1]。滚动轴承的工作机理以及所处的工作环境，使得故障信号的信噪比极低，而早期故障又十分微弱，故而导致故障特征难以提取[2]。现阶段较为成熟的分析算法如Hilbert包络、短时傅里叶、小波变换、Wigner-Ville分布等都有各自的不足。如短时傅里叶窗长度固定、小波变换会造成能量泄漏、Wigner-Ville分布存在交叉项等。2014年，Konstantin Dragomiretskiy等在研究维纳滤波的基础上，参考经验模式分解(Empirical Mode Decomposition ，EMD)提出了变分模态分解(Variational Mode Decomposition，VMD)[3]。该方法通过在变分框架内求解最优变分模型来求取模态分量。WangYanxue等对其进行研究，并使用VMD对转子碰模故障进行分析诊断，取得了良好的效果[4]错误！未找到引用源。。TripathyRK等深入研究VMD并将其引入医学心电图研究中，提高了诊断的准确率[5]。李志农等人将其应用于机械的故障诊断中，验证了该方法能够揭示出碰模故障数据的频率结构，区分碰模故障的严重程度[6]。马增强等将Teager能量算子引入VMD中，对滚动轴承故障进行精确诊断，取得了良好效果[7]。但VMD的结果依赖于预先给定的模态数K，K的选取决定了最终的分解结果，K过小，则无法有效反应信号的特征信息，而K过大，则会导致频率混叠、过分解等现象，因此K的选择尤其重要。

2011年，Ingrid Daubechies等提出了同步压缩变换(Syn-chrosqueezing transform，SST)[8]，同时结合小波变换所构成的同步压缩小波变换(Synchrosqueezing Wavelet Transform，SWT)方法能够通过对小波变换后的小波系数进行重组，将相同频率下的尺度相加，从而抑制能量泄露，提高时频分辨率。Gaurav Thakur等对其进行深入研究并将其引入古气候分析中，取得理想效果[9]。Roberto HHerrera等将此方法用于地震波检测分析中，提取出较为清晰的波形特征[10]。SWT能够有效处理频率较低及缓慢变换的信号中的噪声，但当信号处于强噪声中时，该方法难以达到理想效果。而在实际工程中，滚动轴承的工作环境及工作机理会造成提取的信号中夹杂着较大的噪声，导致无法有效提取信号的时频特征。

峭度是描述随机变量分布特性的数值统计量，反应信号冲击成分的大小。本文将最大峭度指标引入 VMD，选择出最优分解模态数及惩罚因子 α，再利用峭度指标选择有效VMD分解分量从而从噪声信号中提取出有效信息，最后使用 SWT提取信号中的时频特征，从而有效判断滚动轴承的运行状态。相比于EMD等方法来说，VMD具有严谨的理论支撑，且是根据中心频率选取模态数，提高了计算效率，能够将原始信号进行分解从而获得K个含有不同频率成分的模态分量；SWT方法虽然能够提高时频谱的可读性，但当噪声较大时仍然无提取出有效特征，而工业现场会由于环境、滚动轴承工作机理等会造成故障振动信号中包含很大的噪声，导致信噪比极低，将VMD引入SWT中，能够将原始信号进行分解，从而提取出含有有效频率成分的模态分量，提高信噪比，再使用 SWT进行分析，从而有效提取信号的时频特征。

1 变分模态分解VMD

VMD方法参考了 EMD算法，借助了內禀尺度分量（Intrinsic Scale Component，ISC）的概念，重新定义为一个调频调幅信号[11]。

式中，φk(t)非递减，；包络线非负，Ak(t)≥0；瞬时频率；Ak(t)及ωk(t)相对于φk(t)来说是缓变的。因此，在区间内，uk(t)可看作是幅值为 Ak(t)且频率为ωk(t)的谐波信号。

可以通过如下步骤构造出变分模型：1）借助Hilbert变换获得各模态函数uk(t)的解析信号，从而获得信号的单边频谱；2）通过指数修正，将每个围绕各自估算的中心频率的模态函数调制到响应基频带；3）通过高斯平滑解调信号获得每段带宽，即L2范数梯度的平方根。受约束的变分模型为：

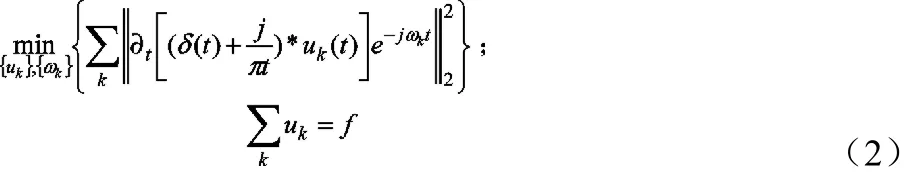
引入惩罚因子α构造增广Lagrange函数从而求取上述变分模型的最优解，Lagrange构造函数如下：

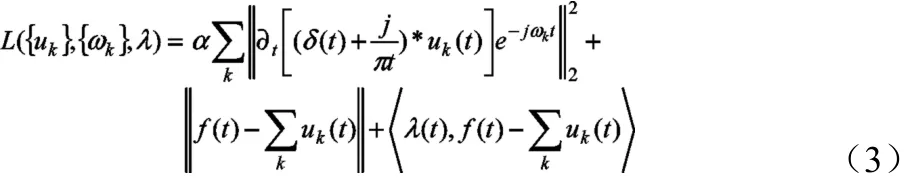
式中：α为惩罚因子；λ为Lagrange乘子。

将上述Lagrange函数从时域变换到频域，求解相应的极值，可得到uk和ωk的频域表达式。

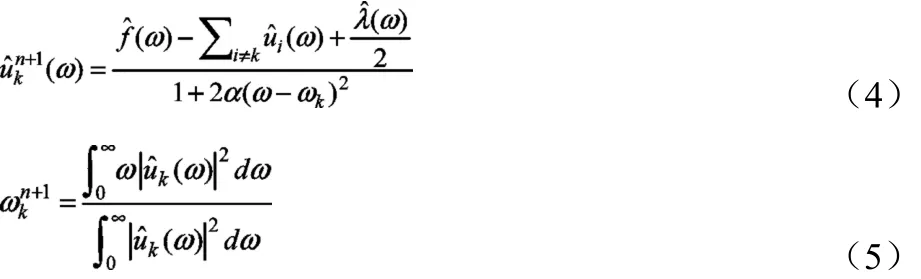
再利用交替方向乘子算法(Alternate Dirsplimi Method of Multipliers，ADMM)求取变分模型的最优解，从而实现VMD分解。算法具体步骤如下：

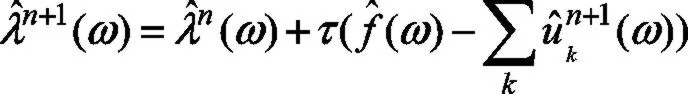
由上述步骤即可将信号分解成K个模态分量。

2 同步压缩小波变换

峭度(Kurtosis)是反映振动信号分布特性的数值统计量，是无量纲参数，对信号的冲击十分敏感，适用于表面损伤类故障，尤其是早期故障的诊断[12]：

在轴承正常运转状态下，其振动信号的幅值分布接近正态分布，当故障开始出现时，信号幅值的分布会偏离正态分布，峭度值也随之增大。峭度指标的绝对值越大，说明轴承偏离其正常状态，故障越严重。

同步压缩小波变换(SWT)能够在一定程度上有效抑制噪声，改善小波变换的能量泄露，提高时频分辨率[13]。

利用CWT对信号x(t)进行处理，可定义为：

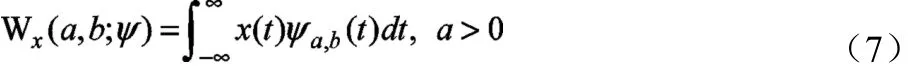
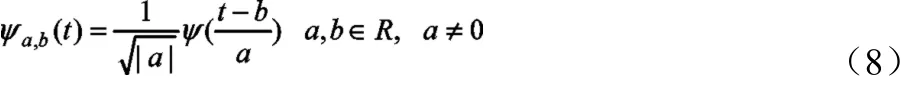
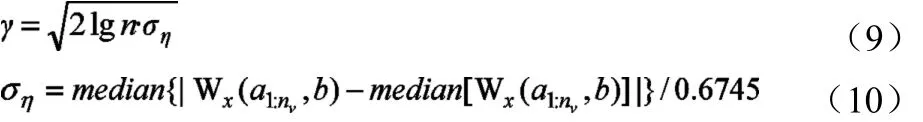
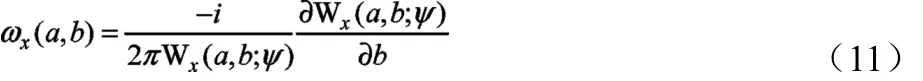
此时便可将任意频率 ωl周围上的值压缩到 ωl上，从而获取同步压缩变换的值，提高时频分辨率。同步压缩变换可定义为：

同步压缩小波变换的逆变换(ISWT)定义为：

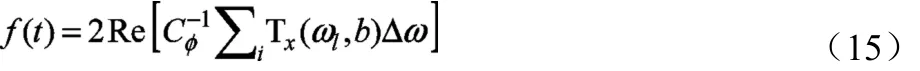
其中

改进SWT的算法(VSWT)流程如下：

（1）初始化VMD参数：分解层数K=2(K∈[2,15])，惩罚因子 α=10(α∈[10,2000])；

（2）计算各模态分量的峭度值，选出最大值，令K=K+1，重新计算峭度值，以此类推算出所有K情况下各模态分量的峭度值，选出所有K情况下峭度的最大值进行比较，最大的峭度值所在的K即为最优值；α=α+10；

（3）同理计算出最优α值(α步长为10)；

（4）将计算出的最优K和α带入VMD中，使用VMD将信号进行分解；

（5）计算各模态峭度值，选出含有最大峭度值的模态分量；

（6）使用SWT对选出的模态分量进行分析。

本文提出使用最大峭度法提取出VMD的最优参数，将VMD引入SWT算法中构成一种新的分析方法(VSWT)，首先使用峭度指标判断出VMD最优参数，再将提取出的参数带入VMD中对原始信号进行分解，最后领用峭度指标提取有效模态分量后使用 SWT进行处理分析，提取出信号的时频特征，从而对滚动轴承运转状态进行判断。

3 仿真分析

通过构造一组仿真故障信号ft进行分析以便验证提出方法的有效性。该信号构造轴承故障的仿真信号，其中轴承的固有频率f=3000Hz，位移常数y0=5，阻尼系数ζ＝0.1，冲击故障发生的周期为 0.01s，采样频率 fs=20kHz，采样点数N=4096：

对信号加入信噪比(SNR)为-5的高斯白噪声，图1a和1b分别给出了原始信号和加噪信号幅值谱。首先设定VMD的初始化模态数为 K=2，惩罚因子α=10，对信号进行 VMD分解，计算各模态的峭度值，选择最大的峭度值作为K=2时的峭度，对K进行叠加直至K=15停止，比较各模态数下的最大峭度值，图1c给出了各模态数下的最大峭度值，从图中可以看出K=7时峭度最大，因此模态数K定为7。同理对惩罚因子进行优化，图1d给出了各惩罚因子下的最大峭度值，从图中可以看出当 α=20时峭度值最大。由上述步骤确定VMD的模态数K=7，惩罚因子α=20，使用VMD对信号进行分解，图1d给出了VMD的分解后各模态分量的幅值谱。计算各模态分量的峭度值，第一层峭度最大，达到了4.9201，因此选择第一层模态分量为有效分量，使用 SWT对其进行处理，图2给出了SWT处理结果。

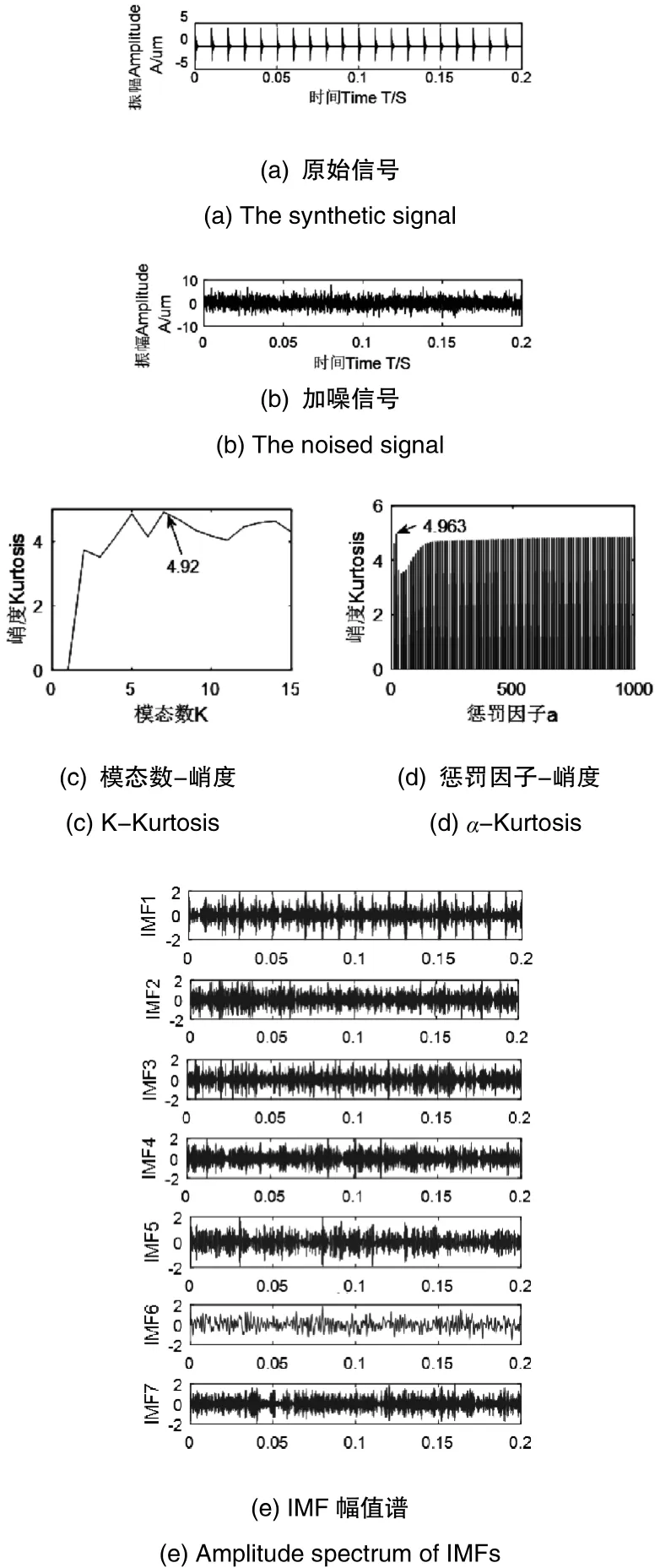
图1 VMD分解Fig.1 Variational Mode Decomposition

图2(a)给出了原始信号的SWT处理结果，可以看出2000至4000Hz之间，以3000为中心频率有一条清晰的能量集中带，图 2(b)给出了加噪信号的 SWT处理结果，反应出特征频率已经完全淹没在噪声之中，图 2(c)给出了对加噪信号使用VSWT处理的结果，从图中可以反映出在3000附近出现了很强的能量集中带，其他位置的噪声已基本滤除，充分说明了本文所提出方法的可行性与有效性。

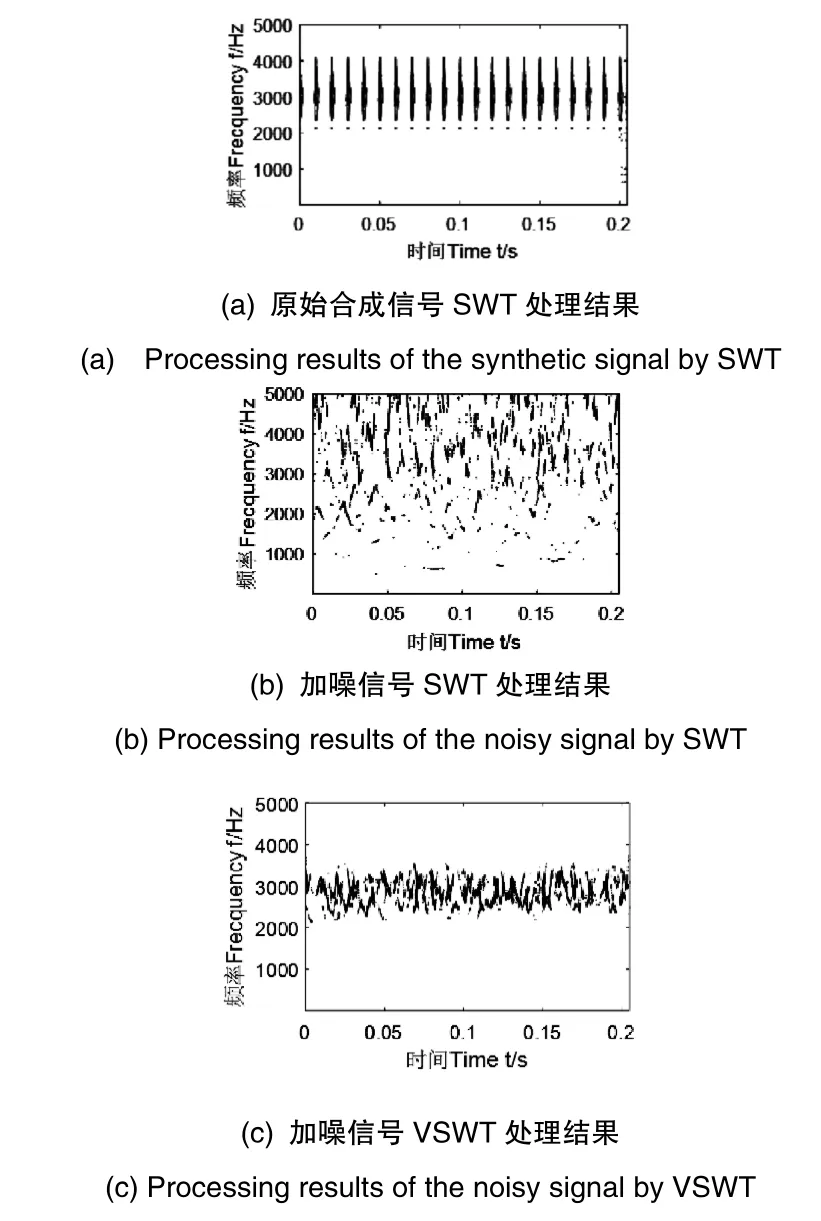
图2 SWT处理结果Fig.2 Processing results by SWT

图3给出了使用从图3中可以反映出除边缘部分有少量差别以外，其余部分高度吻合，反映了VSWT具有较高的重构能力。

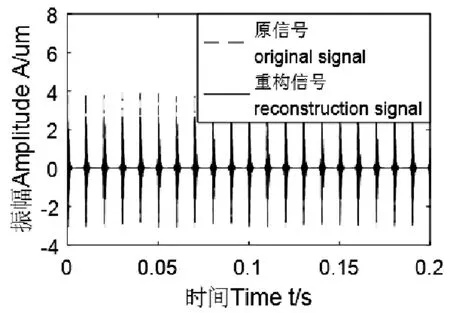
图3 原信号与重构信号对比Fig.3 The original signal and the signals reconstructed by IVSWT

综上所述，可以判断出VSWT具有良好的抗噪能力以及较高的信号提取精度，能够在强噪声背景下有效提取信号时频特征，提高时频可读性，同时能够有效的重构信号。

4 实验和验证

4.1 实验说明

为验证改进 SWT的工程实用性，本文以深南电路钻孔工序的钻床为实验平台，通过更换故障轴承采集滚动轴承正常振动信号、外圈故障信号、内圈故障信号、滚动体故障信号，分别应用 Hilbert包络、SWT、VSWT分析故障信号，通过提取的时频特征判断滚动轴承的故障类型。

通常滚动轴承常见的故障类型为外圈故障、内圈故障以及滚动体故障。其故障特征频率计算公式为：

内圈故障特征频率

外圈故障特征频率

滚动体故障特征频率

式中，fr为转频；d为滚珠直径；D为节圆直接； 为接触角；Z为滚珠数。

图4 轴承故障类型Fig.4 The type of bearing fault

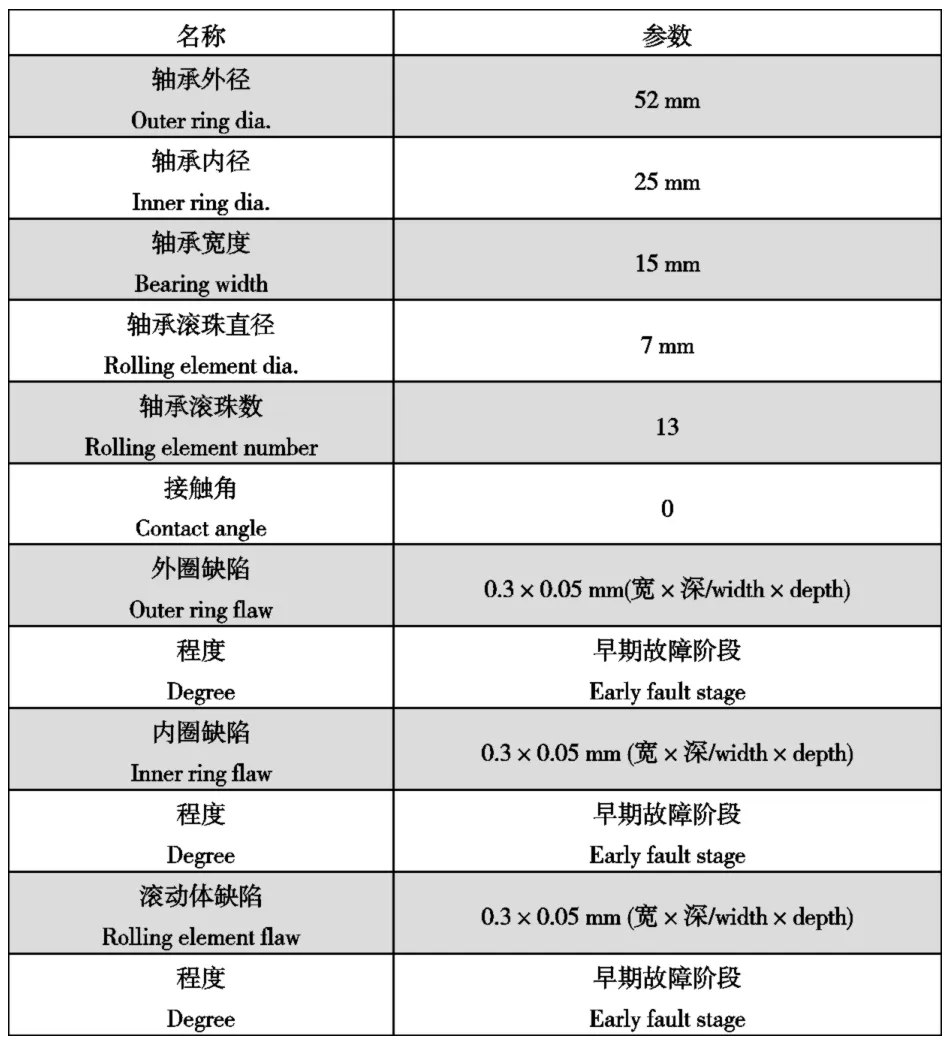
表1 轴承参数Tab.1 Parameter of bearing

实验平台采用PCB MA352A60型加速度传感器，采集垂直方向的振动信号数据，实验滚动轴承具体参数见表 1。该实验转速设定为1000r/min，采样频率fs为50 kHz。以工程实际中滚动轴承故障现象为参照，利用线切割加工技术，在试验台滚动轴承外圈加工0.3×0.05(宽×深)微小凹痕模拟外圈故障；在试验台滚动轴承内圈加工0.3×0.05(宽×深)微小凹痕模拟内圈故障；在试验台滚动轴承内圈加工0.3×0.05(宽×深)微小凹痕模拟滚动体故障，具体现象如图4所示。由式(18)～式(20)可求得其外圈、内圈和滚动体的故障特征频率分别为88.64Hz、128.03Hz以及44.32Hz。

4.2 信号处理及分析

对采集的故障信号进行处理，图5给出了滚动轴承正常振动信号、外圈故障振动信号、内圈故障振动信号以及滚动体故障振动信号的时域波形图。

图5 轴承振动信号Fig.5 The bearing vibration signal

为验证改进 SWT方法的有效性与实用性，本文使用不同方法处理滚动轴承故障数据，并对处理结果进行比较。

图6给出了外圈故障信号处理结果。使用Hilbert包络对故障故障信号进行处理，结果如图6a所示，含有噪声较大，特征频率完全被噪声淹没，从图中找不出任何特征。图 6b为 SWT处理后的时频谱，同样，从图中找不到任何特征。使用本文提出的改进SWT(VSWT)进行处理，首先确定VMD分解的模态数和惩罚因子，令K=2，α=10，使用VMD进行分解，求取个模态的峭度值，选取最大的值作为K=2时的最大峭度值，保持α不变，令K=K+1(K∈[2,15])，同样求出此时的最大峭度值，以此类推，求出不同K值下的最大峭度值，选择所有最大峭度值中的最大峭度值所在的模态数K，此时K即为最优解，同理求取最优惩罚因子 =10( ∈[10,2000])，从图6d～图6e中可以看出当K=3，α=180时，峭度最大，分别为62.72和64.36，确定VMD参数后使用VMD对信号进行分解，经计算第3层峭度值最大，达到了64.3655，故选择第3模态作为SWT输入信号，使用SWT进行处理，结果如图6c所示，从图中可以看出，在89.27Hz、180.03Hz、265Hz、355.09Hz处都出现了清晰的能量集中带，与外圈故障特征频率的1倍频88.64Hz、2倍频177.28Hz、3倍频265.92Hz、4倍频354.56Hz较为接近，由此可以判断滚动轴承外圈出现了故障，与实验结果一致。

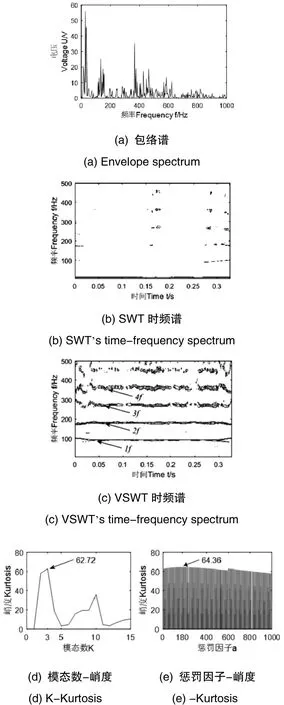
图6 外圈故障信号处理结果Fig.6 Processing results of outer ring fault signal

针对内圈故障信号，使用上述的同样方法进行分析。图7a和图7b分别给出了Hilbert包络后的包络谱及SWT后的时频谱，由于采集过程中噪声较大以及其他因素干扰，从图无法找出任何特征。使用VSWT进行处理，首先确定VMD分解的模态数和惩罚因子，令K=2，α=10，使用VMD进行分解，求取个模态的峭度值，选取最大的值作为K=2时的最大峭度值，保持α不变，令K=K+1(K∈[2,15])，同样求出此时的最大峭度值，以此类推，求出不同K值下的最大峭度值，选择所有最大峭度值中的最大峭度值所在的模态数K，此时K即为最优解，同理求取最优惩罚因子 =140( ∈[10,2000])，从图7d～图7e中可以看出当K=9，α=140时，峭度最大，分别为67.93和72.78，确定VMD参数后使用VMD对信号进行分解，经计算第9层峭度值最大，达到了72.7765，故选择第9模态作为SWT输入信号，使用SWT进行处理，结果如图 7(c)所示，从图中可以看出，虽然周围仍存在噪声，但在130.27Hz、255.89Hz处都出现了清晰的能量集中带，与外圈故障特征频率的1倍频128.03Hz、2倍频256.06Hz、较为接近，由此可以判断滚动轴承内圈出现了故障，与实验结果一致。

图7 内圈故障信号处理结果Fig.7 Processing results of inner ring fault signal

针对滚动体故障振动信号，使用同样方法进行分析。图8(a)和图8(b)分别给出了Hilbert包络后的包络谱及SWT后的时频谱，同样，由于噪声较大以及滚动体早期微弱故障较难提取等因素，从图无法找出任何特征。使用VSWT进行处理，同理，从图8(d)-8(e)中可以看出当K=3，α=550时，峭度最大，分别为245.5和292，确定VMD参数后使用VMD对信号进行分解，经计算第3层峭度值最大，达到了292.0223，故选择第3模态作为SWT输入信号，使用SWT进行处理，结果如图8(c)所示，从图中可以看出，虽然周围仍存在噪声，但在45.07Hz、90.28Hz处都出现了较为清晰的能量集中带，与滚动体故障特征频率的1倍频44.32Hz、2倍频88.64Hz、较为接近，由此可以判断滚动轴承滚动体出现了故障，与实验结果一致。

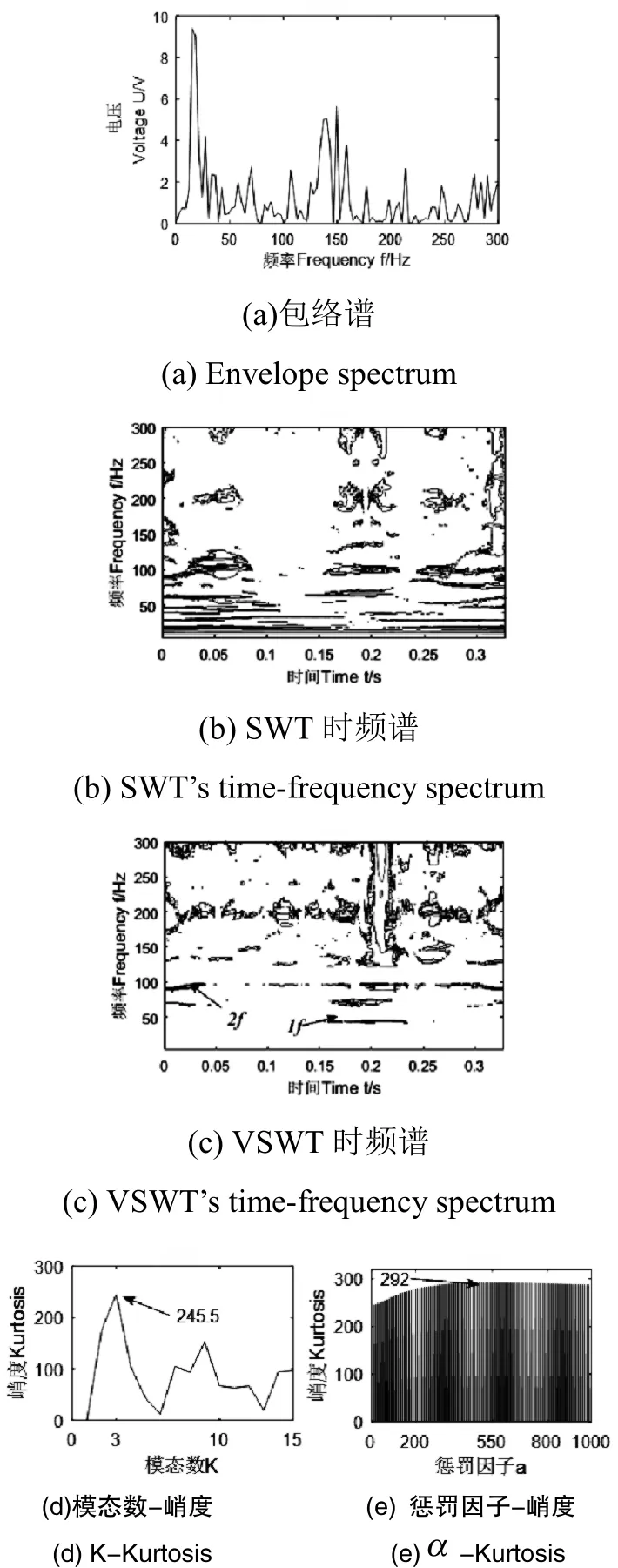
图8 滚动体故障信号处理结果Fig.8 Processing results of rolling body fault signal

经实验验证，使用常见分析手法，如Hilbert包络、SWT等提取强噪声背景下的滚动轴承早期微弱故障振动信号已较为困难。VSWT通过使用峭度指标优化VMD的模态数K及惩罚因子α，使用VMD对信号进行分解后根据最大峭度原则选择含有有效信息最多的IMF，使用SWT对提取出的最优模态分量进行处理从而提取有效时频特征。相比 SWT而言，VSWT能够很好的处理强噪声背景下的故障信号，优势显著。

5 结论

本文研究同步压缩小波变换(SWT)结合引入最大峭度原则的变分模态分解(VMD)所形成的 VSWT方法能够将信号分解成K个模态分量，不同的模态分量包含不同的频率特征，根据最大峭度原则选择最优IMF作为SWT的输入信号，即利用CWT对有效IMF进行处理，再使用SST对CWT得到的系数进行压缩，最后实验结果表明，该方法能够有效抑制噪声，即使在较强的噪声背景下，也能够从信号中提取出有效特征频率，同时VSWT也具有较高的时频分辨率。