基于R的新疆GDP分析与预测
2019-04-10张行行
张行行

摘要:根据新疆地区历年GDP数据的特点,基于R语言,建立求和自回归移动平均模型ARIMA(p,d,q)。通过对数和差分运算对数据进行平稳化处理,根据自相关系数、偏自相关系数以及单位根检验判断其平稳性,选择合适的ARIMA模型,进行预测和比较,得到较为满意的结果。
关键词:R语言 GDP ARIMA模型 新疆
一、引言
R语言[1]作为一款自由的开源软件,不仅具有强大的统计分析功能和统计制图功能,而且拥有强大的软件包生态系统,其源代码可供我们直接查看并进行扩展而无需申请权限。所以近年来,R语言在学界和业界受到了越来越多的重视。在国外高校统计学科,R几乎是一门必修的语言。新疆地处中国西北部,资源丰富,土地面积占全国的1/6,与8个国家毗邻,是东西方文化的聚集地。同时它地处亚欧大陆腹地的十字大通道,是贸易互联互通的通道,是新丝绸之路经济带的核心建设区以及我国向西开放的重要门户[2]。作为衡量地区经济发展的重要指标,GDP不仅可以反映一个地区的经济表现,还是影响社会稳定的重要因素。因此利用时间序列模型针对新疆GDP发展趋势进行预测,对于制定经济发展目标、战略规划布局具有重要意义。
对于GDP的发展规律和预测一直是经济学家关注的热点和难点,纪广月[3]以广东省2006-2011年GDP与第一、第二、第三产业的历史数据为依据,利用灰色关联分析方法,建立灰色预测模型GM(1,1),对未来几年的广东省GDP进行了预测;JamesSpencerL等[4]利用210个国家1950-2015的人均GDP序列,建立了一个综合模型,并允许每年更新数据;张淑红等[5]基于1978-2010年的人均GDP指数使用时间序列分析中的Box-Jenkins方法进行定阶,建立了线性自回归模型,得到了较好的拟合和预测结果;苏玉华等[6]运用SAS8.0系统对1978-20006年广西生产总值建立ARIMA模型,并做了预测分析;范玉妹等[7]利用EViews软件应用ARMA模型对北京市人均GDP进行拟合,效果良好,并预测了2010年至2014年的数据。由于大多数研究使用SAS、Eviews或SPSS进行建模分析,使用R语言来分析的文章很少,本文应用R语言以新疆1985至2017年的GDP数据为样本,对其进行统计分析,建立ARIMA(2,2,0)模型,并对2018-2020年新疆GDP进行预测,以期对经济政策目标制定者提供决策参考。
二、ARIMA模型理论概述
ARIMA模型本质上是将差分运算与自回归移动平均(ARMA)模型相结合,即利用差分运算使非平稳序列显示出平稳序列的性质,再使用ARMA模型进行拟合。此模型可以有效提取非平稳序列的确定性信息,弥补确定性因素分解方法的不足以及ARMA模型的局限性,进行精确有效地短期预测。ARIMA(p,d,q)模型的一般结构为:
式中
其中,d为差分阶数,p、q分别为模型中自回归AR与移动平均MA的滞后期数,、为多项式系数,为白噪声序列,为所选取的时间序列。通常情况下,ARIMA模型遵循如下分析步骤:
Step1:考察时间序列的特征,对其平稳性进行检验;
Step2:平稳化处理,利用对数或差分运算转化为平稳序列;
Step3:拟合ARMA模型,确定参数;
Step4:进行白噪声检验;
Step5:利用所建模型进行预测分析。
三、ARIMA模型实证分析
(一)数据资料
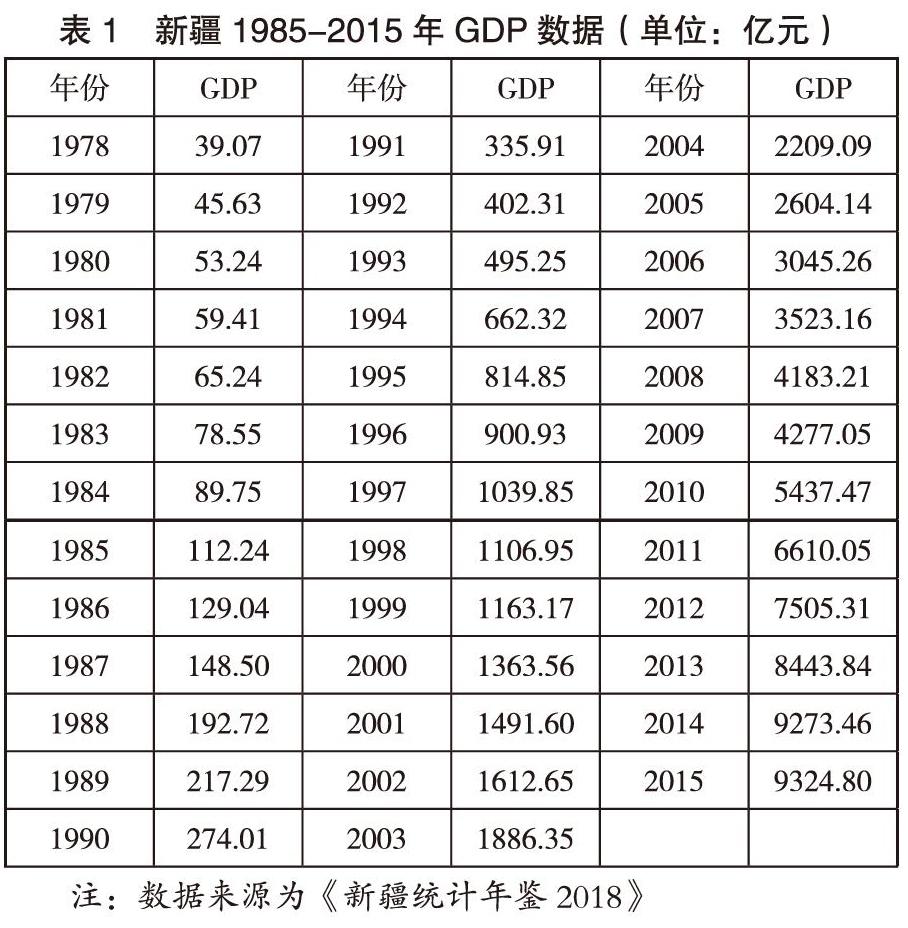
本文选取新疆改革开放以来的数据,即1978至2015年的GDP数据(见表1)作为研究对象进行时间序列分析,基于R语言环境建立ARIMA(p,d,q)模型,并对2016—2017年的数据进行预测,与实际值进行比较;在此基础上,对2018-2020年新疆GDP进行预测分析。
(二)判断序列特征
为初步判断GDP序列的特征和平稳性,由表1看出,新疆是一个经济持续增长的经济体。从1985至2015年新疆GDP呈现明显的上升趋势,无周期性,为非平稳序列。故需对数据进行平稳化处理,使其满足平稳性和零均值的建模要求。
(三)序列的平稳化处理
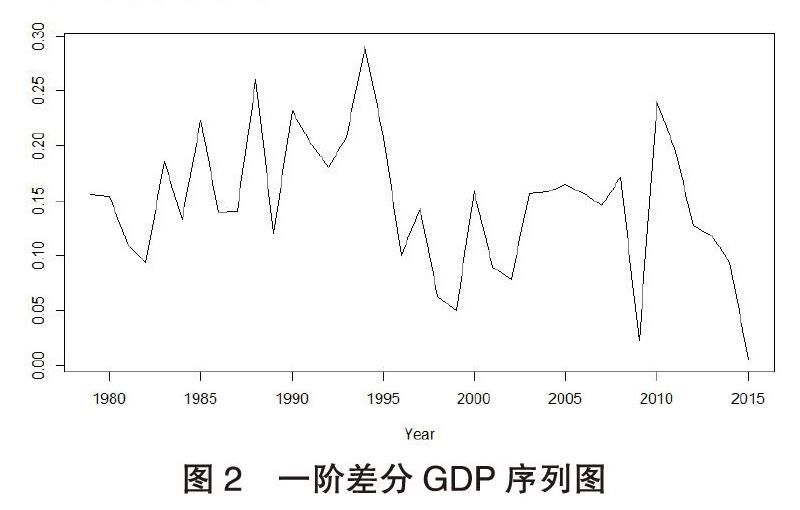
由于新疆GDP序列呈现出指数增长趋势,故需对该序列取对数消除指数趋势,并对其进行一阶差分处理以消除线性趋势,得到如图2所示的时间序列图。从图2中可以观察到:均值不为零,其趋势性已基本消除,但是否为平稳序列,需要进一步的平稳性检验。
本文采用ADF单位根检验法来判断序列的平稳性,所得结果如表2所示。
检验结果显示,新疆GDP对数差分序列的ADF检验P值均大于显著性水平α=0.01、0.05,落在拒绝域外,不能显著拒绝序列为非平稳的原假设,说明该序列为非平稳序列,故对其进行二次差分运算。检验结果表明所得ADF检验P值普遍小于显著性水平α=0.01、0.05,显著拒绝原假设,故二阶差分后的对数序列为平稳序列。
(四)拟合ARIMA(p,d,q)模型
由序列平稳化的过程可知,ARIMA(p,d,q)模型中的差分阶数d=2。自回归阶数p与移动平均阶数q的确定可以通过样本的自相关函数与偏自相關函数的观察获得。将经过平稳化处理后的新疆GDP时间序列命名为DGDP序列,并绘制自相关函数(ACF)和偏自相关函数(PACF)图,如图3所示。
从图3中可以看出,二者均具有明显的拖尾性,且自相关系数一阶显著不为零,一阶之后都近似为零,偏自相关系数2阶显著不为零,2阶之后都近似为零。因此可选择的模型有ARIMA(2,2,1),ARIMA(2,2,0),ARIMA(1,2,1),ARIMA(1,2,0),对这四个模型分别进行评判和比较,见表4。
AIC准则是拟合模型的似然函数值与模型中未知参数个数的加权函数,通过综合考虑拟合模型的拟合精度和未知参数个数寻找相对最优模型;SBC准则是AIC准则的改进,它将AIC函数中未知參数个数的惩罚权重由常数2变成了样本容量的对数函数ln(n),解决了样本容量趋于无穷大时AIC准则选择的模型不收敛于真实模型的问题。公式如下:
其中,ML为极大似然函数值,n为样本容量。在初选模型中,使得AIC或SBC函数达到最小的模型为相对最优模型。显然,由表4可知,ARIMA(2,2,0)优于其他模型。用R3.4.4的box.test()函数对其进行残差自相关检验,得到的P值都显著大于α=0.05,可认为残差序列为白噪声序列,说明模型ARIMA(2,2,0)显著有效。
(五)模型的预测和分析
为检验模型的预测效果,下面对新疆2016、2017年的GDP进行预测,并与实际值进行比较,数据来源《新疆统计年鉴2018》,结果如表5:
由对照表可知,预测结果与真实值相差在5%以内,用ARIMA(2,2,0)可以较好地拟合新疆GDP的实际值。
利用此模型对2018-2020年新疆GDP进行预测分析,其结果见表6:
四、结语
本文通过对新疆1978至2017年的GDP数据作为研究对象进行时间序列分析,结合R语言建立了ARIMA(2,2,0)模型,并通过一系列检验证明了其有效性,并对2018-2020年新疆GDP进行预测分析,从预测结果来看,新疆生产总值呈现出稳步增长的趋势,且增长率逐年提高。结论表明,所建立的ARIMA模型可以有效地拟合样本数据,预测未来走势,具有较强的短期预测能力,从而为经济决策的制定和调整提供参考。
参考文献:
[1]汤银才.R语言与统计分析[M].高等教育出版社,2008.
[2]刘艳芝.“一带一路”背景下的新疆经济发展研究[J].经济论坛,2016(02):30-32.
[3]纪广月.基于灰色关联分析的广东省GDP与产业结构之间的关系及GDP预测的数学模型[J].数学的实践与认识,2013(15):198-203.
[4]JAMES S L,GUBBINS P,MURRAY C J,et al. Developing a comprehensive time series of GDP per capita for 210 countries from 1950 to 2015[J]. Popul Health Metr,2012,10(1):12.
[5]张淑红,杨万才,武新乾.“十二五”时期河南省人均GDP预测[J].数理统计与管理,2014(03):394-399.
[6]苏玉华,江伟.广西生产总值的时间序列分析[J].贺州学院学报,2009(01):125-128.
[7]范玉妹,玄婧.ARMA算法在GDP预测中的应用[J].江南大学学报(自然科学版),2010(06):736-740.
