WSN中基于指纹匹配的室内定位方法*

竺超明,华子雯,陈立建,徐 慧,毛科技*

(1.浙江广播电视大学萧山学院,杭州 310000;2.浙江工业大学计算机科学与技术学院,杭州 310032)

无线传感器网络WSN(Wireless Sensor Networks)主要用来监测网络部署区域中各种环境特性,比如温湿度、光照强度、磁场强度、受力强度、速度或加速度、化学物质浓度等等,但是只有在知道节点位置信息的情况下很多监测的数据才有意义。换句话说,传感器节点的定位在无线传感器网络的诸多应用中有着十分重要的意义。目前室外定位方法主要是通过全球定位系统GPS(Global Positioning System),GPS卫星通过发射电磁波信号计算距离,从而实现定位功能,然而GPS信号在室内环境或信号穿透比较差的场景中,不能实现高精度定位,因此很难满足室内定位的需求。室内定位方法与成熟的室外定位方法存在较大差异,主要包括:一、室内定位方法需要解决复杂的定位环境对定位精度带来的影响,目前在室内定位中常见的Wi-Fi、蓝牙、Zigbee等定位技术存在多径效应、成本昂贵等问题。二、室内定位方法对环境的依赖性较大,当环境发生变化时很可能导致之前部署的定位系统失效。三、对定位的精度要求不同,室外定位的精度没有严格的要求,而室内环境本身比较小,所以室内定位需要较高的精度,一般为米级甚至厘米级[1-5]。

目前室内定位最常见的是测距定位方法,包括利用蓝牙、Wifi、Zigbee等技术进行测距定位,该定位技术通过信号的衰减从而实现距离的测量,信号衰减越多,认为传输的距离越远。然而在复杂环境下,利用信号强度RSSI进行测距存在诸多问题,测距误差较大[6]。文献[7]提出了无线传感器节点在空间环境上的RSSI相似度概念,采用RSSI相似度作为权重因子,改进了加权质心算法;文献[8]针对基于RSSI的无线传感器网络室内移动目标定位算法易受干扰、波动较大等问题,提出一种改进的RSSI多维标度室内定位算法;文献[9]提出了一种基于RSSI和辅助节点协作的Wi-Fi室内定位方法,适用于基于Wi-Fi的室内定位系统;文献[10]提出一种用于室内定位的基于接收信号强度的二次定位方法;还有很多文献[11-15]都是关于室内定位的,但是在室内场景中需要部署大量的基站节点才能进行定位,成本昂贵,因此很难在实际场景中应用。基于指纹的室内定位方法是通过采集室内定位场景中的固有特征或部署特征,构建定位指纹数据库,然后通过匹配指纹数据库从而实现精度较高的室内定位。

基于信号强度测距的定位方法能够实现较高精度的定位,定位精度一般在毫米到米之间,但是由于测距定位本身存在的缺点,很难应用于实际场景中,而指纹定位方法虽然平均定位精度略低于测距定位,但是指纹定位方法成本低,可靠度高,抗干扰能力强,因此是较好的选择[16-18]。

基于上述分析,本文研究了一种基于信号强度特征的指纹定位方法,该方法通过构建定位区域RSSI特征,构建多维向量指纹实现较高精度定位,且指纹构建方法能够当定位环境发生变化是快速重建指纹,因此能够较好的应用于实际场景中。

1 数据处理及定位指纹构建

1.1 信号强度数据预处理

传感器节点采集的原始数据如图1所示,在发送节点和接收节点固定的情况下,采集的RSSI值波动比较大,这对定位精度存在巨大的影响,因此本文Kalman滤波算法对原始数据进行滤波处理,去除噪声,经过处理后的RSSI值如图2所示。

图1 RSSI原始数据图

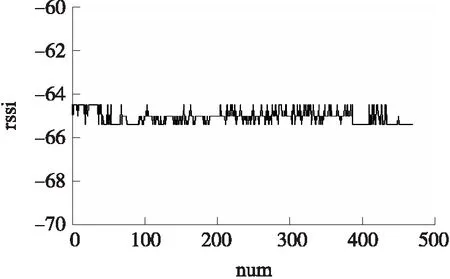
图2 RSSI滤波后结果图

1.2 多维RSSI定位指纹构建

Kriging插值算法主要是对样本的待估计位置相互间的空间位置关系进行了考虑,通过加权平均来估计预测未知区域的情况,从而使插值结果呈现出线性、无偏和最小方差估计的特点[19-20]。由于这种算法是一种光滑内插方法,因此结果随着样本点的增多而更加精确。由于复杂环境的干扰导致RSSI强度不总是呈现出理想情况下以节点为同心圆分布,本文需要一种能在有限的样本点构建出比较符合实际情况的RSSI分布,采用Kriging算法对RSSI进行预测,能根据样本点的数据构建出最能符合实际情况的RSSI分布。本文对传统Kriging算法进行改进,使算法在预测模型选择阶段能够根据数据样本自动选择匹配度最高的经典模型作为最终的预测模型,因此算法具有较强的自适应性。

经过处理后的RSSI值构建定位区域D的指纹数据库,如图3所示。定位区域中总共部署了25个Micaz普通节点,其中包括5个信标节点和20个辅助节点,这些传感器节点都能发射和接收信号。首先锚节点A向外广播信号,其他24个节点能够接收到广播的信号,并从信号中获取RSSI值,由于每个传感器节点的位置是已知的,因此可获得节点的RSSI与节点间距离d的关系对Pair,然后利用Kriging插值算法可构建锚节点A对应的定位区域指纹。然后用同样的方法分别为锚节点B、C、D、E构建定位区域指纹,最终将构建个5个单维指纹做并集,形成一个5维的定位区域向量指纹。利用Kriging插值算法构建一个信标节点(信标节点A)的单维定位指纹具体过程如图4所示,具体步骤如下:

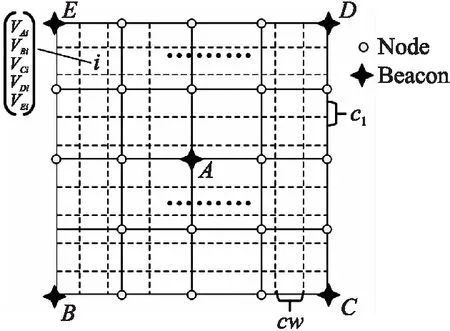
图4 定位指纹构建图

第1步:将长为L,宽为W的定位区域D均匀划分为m行n列,定位区域D被划分为m×n个方格,每个方格的长度为cl=L/m,宽度为cw=W/n。

第2步:利用信标节点和辅助节点采集的RSSI值训练Kriging插值算法,然后对步骤一划分的小格子进行插值,这样就建立了锚节点A对应的单维RSSI指纹VA,其中VA表示定位区域中每个方格子(子区域)对应的RSSI值和坐标。

第3步:对锚节点B、C、D、E重复步骤二,此时能构建单维RSSI定位指纹VB、VC、VD、VE,最后将构建的5个单维指纹做并集,得到一个5维的RSSI指纹FingerP,如式(1)所示。

FingerP[m×n][5]=VA[m×n]∪VB[m×n]∪
VC[m×n]∪VD[m×n]∪VE[m×n]

(1)

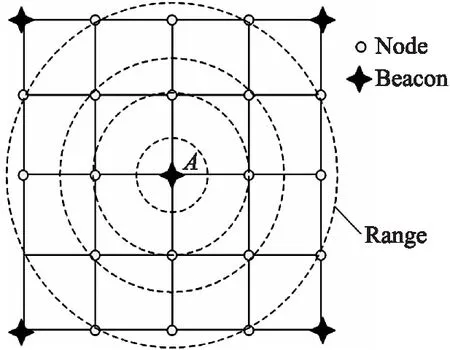
图3 定位区域节点部署图

2 指纹匹配定位方法及结果优化

2.1 匹配定位

当目标节点进入定位区域后会固定时间向传感器网络的5个信标节点发送数据包,表示开始定位,锚节点收到数据包后立刻向目标节点发送空的数据包,目标节点收到5个锚节点的数据包后,从数据包中获得RSSI值,然后对RSSI值进行异常处理,形成一个可靠的5维向量,如式(2)所示,这个5维向量和定位指纹地图中的m×n个方格对应的5维RSSI向量进行余弦相似度匹配,匹配结束后选择相似度最高的前num个方格作为目标节点所在位置的范围,实现初步的定位。

图5 障碍物影响图

(2)

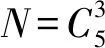
表1 向量组合匹配方法

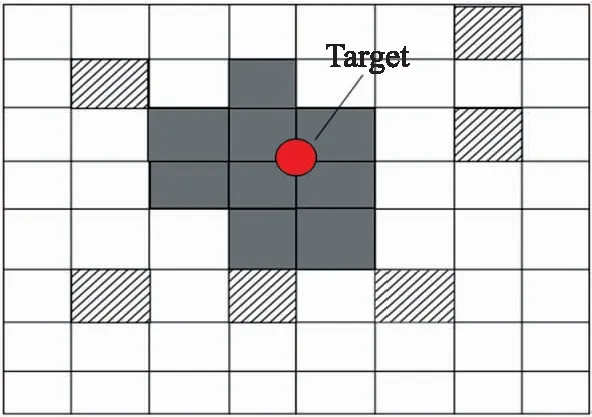
图6 匹配结果图

2.2 定位结果优化

如图6所示。虚阴影部分表示误差较大的格子,实阴影部分表示误差较小的方格子,圆表示目标节点的实际位置。为了排除定位误差较大的方格子,本文采用文献[21]的K-means聚类算法提高定位精度。首先利用K-means聚类算法将num个方格子聚为Nc类,最后选择元素最多的一类作为目标节点的真实位置范围,而其他元素较少的类认为是定位误差,需要排除。最后将元素最多的一类的重心作为最终的定位结果,如图7所示。

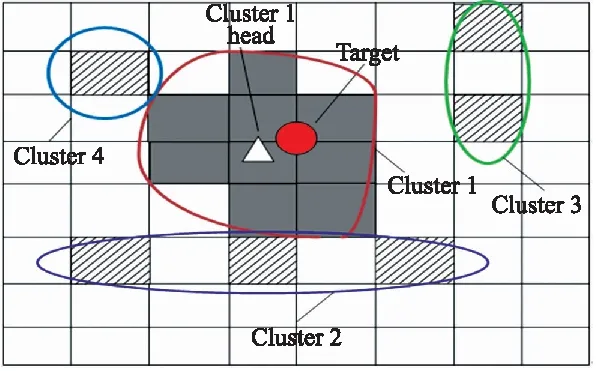
图7 定位结果图

3 实验分析

3.1 实验环境设置

定位区域为一个3 m×3 m的室内环境,在定位区域中部署25个传感器节点(Micaz节点的主频为4 MHz,功率:3 mW),其中5个锚节点、20个位辅助节点,验证定位算法的抗干扰能力,定位场景如图8所示。系统中的定位目标为一辆搭载目标传感器节点的小车,如图9所示,目标小车通过蓝牙与手机连接,目标小车在定位区域内行走,定位系统的界面中存在一个虚拟的定位区域,实时画出目标小车的位置,如图10所示。

图8 定位场景图

图9 定位目标图

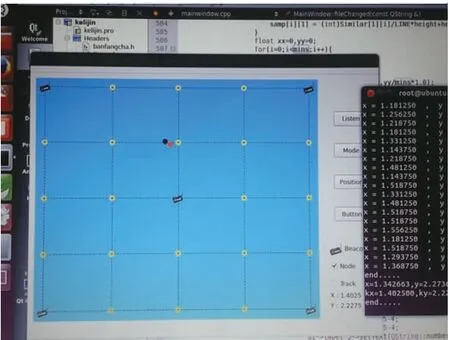
图10 系统界面图

3.2 实验结果分析

3.2.1 Kriging插值精度

为构建精确的定位指纹地图,本实验在定位区域中均匀部署不同数量的传感器节点,实验中选择定位区域内4个不同位置作为插值准确性的验证点,这4个点的坐标分别为a(0.75,0.75)、b(2.25,0.75)、c(0.75,2.25)、d(2.25,2.25),实验中在定位区域中心部署一个传感器节点,该节点向外广播信号,而定位区域中其他节点接收信号并获得RSSI值。分别实际采集4个实验点的RSSI值和Kriging插值得到的RSSI值,最后将4个实验点的平均RSSI值作为实验结果进行对比。实验结果如图11所示,横坐标表示定位区域中部署节点的数量,这些节点用于采集Kriging算法的样本点,纵坐标表示4个实验点的平均RSSI值。

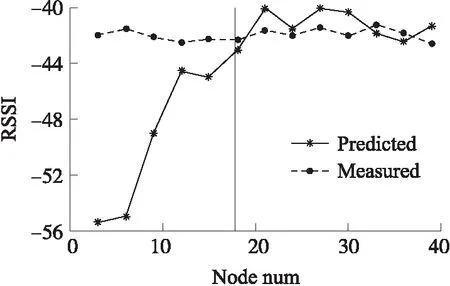
图11 插值结果对比图

实验结果表明在前期定位区域中部署的传感器节点增加,利用Kriging算法插值得到的RSSI值逐渐靠近真实采集的RSSI值,当传感器节点数量大于18个以后,插值得到的RSSI值与实际采集的RSSI值基本相同,但是任存在微小差别,因为传感器节点的信号受自身的影响,接收节点采集的RSSI值任存在跳动的情况,另一方便插值算法计算得到的RSSI值也收到样本RSSI的影响,但是误差是在可接受的范围内。实验结果表明在长为3 m,宽为3 m的定位区域中部署传感器节点的数量不少于18个时,利用Kriging算法构建定位区域指纹是可靠的。

3.2.2 区域划分对定位精度的影响

本文的指纹定位方法将定位区域划分为m×n个格子,每个格子的大小相同,利用Kriging插值算法为每个格子预测其对应的RSSI值。实验中传感器节点的部署方式如图8所示,均匀的部署25个传感器节点,其中5个锚节点,20个辅助节点,将定位结果均匀的划分为若干方格子,实验结果如图12所示,横坐标为将定位区域划分的精细程度,纵坐标为定位系统的定位误差,实验结果是20次随机定位的平均结果。

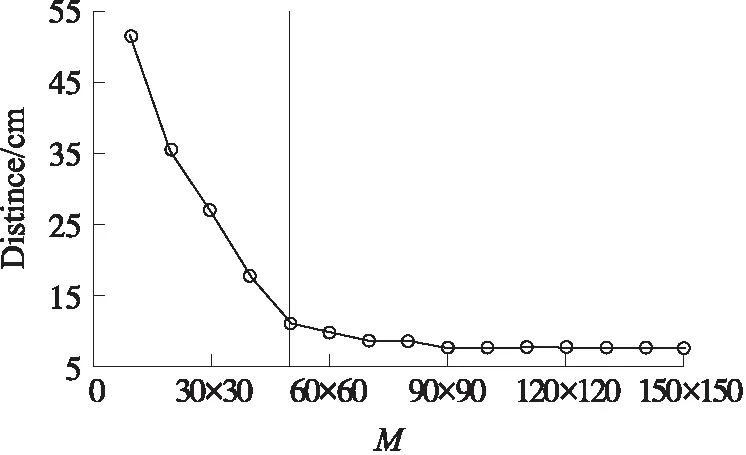
图12 定位区域划分效果图

实验结果显示初始时刻随着定位区域划分越来越精细,定位系统的定位误差逐渐减小,当定位误差减小到10 cm左右后随着定位区域划分的越来越精细,定位误差降低的幅度逐渐减小,最后趋于稳定。当定位区域被划分为50×50的精细度时,定位误差逐渐稳定下来,因为此时每个方格的长度为6 cm,宽度为4 cm,这和传感器节点的表面积大小接近,因此即使对定位区域划分的更精细,定位的精度也不会有大幅度提高。通过本次实验得出结论:定位区域划分的精细程度和算法的定位精度有很大的关系,在一定程度上,划分的越精细,定位精度越高,但是当每个小格子面积与传感器节点面积接近时,定位精度也就趋于稳定。

3.2.3 定位算法抗干扰性

为了使室内定位算法具有较强的抗障碍物干扰性,设计了基于组合匹配的定位方法。假设多个锚节点与目标节点的视距通讯链路被障碍物干扰的数量有Onum条,则只需要满足Bnum-Onum≥3即可对目标节点进行正常定位,其中Bnum为锚节点的数量。定位系统的节点部署方式如图8所示。锚节点节点与目标节点被障碍物遮挡的情况如图9所示。本次实验验证目标节点ob(1.6,1.4)的定位精度与5个锚节点被遮挡视距链路数量的关系,实验结果如图13所示,横坐标表示被遮挡的链路数量,纵坐标表示对目标节点的定位误差,实验结果是系统重复定位的20次平均结果。

图13 组合匹配结果图

实验结果表明当被遮挡的链路数量分别为0、1、2时(总共有5个锚节点),系统的定位误差约为6 cm～8 cm,定位误差比较小,当被障碍物干扰的链路数量分别为3、4、5时,能够与目标节点视距通讯的链路数量分别为2、1、0,此时的定位误差较大,基本为1.5 m、1.8 m、2.2 m,而定位的范围仅仅是一个边长为3m的正方形区域,因此这么大的误差并不能被接受。实验结果表明本文提出的基于组合匹配的方法有较好的抗障碍物干扰能力。

3.2.4 定位优化结果

仅采用与定位指纹匹配度最高的一个位置作为定位结果存在较大的偶然性,因此本文选择匹配度最高的前n个位置作为初步的定位结果范围,然后采用K-means聚类算法对定位结果范围进行聚类。通过实际的定位系统实验验证在没有采用K-means聚类方法(直接计算n个定位结果的重心作为定位结果)和采用了K-means聚类方法对系统整体定位精度的影响,实验结果如图14所示,横坐标为实验次数,纵坐标为系统的平均定位误差。每次实验都是随机定位10次的平均结果。

图14 定位结果优化图

实验结果表明采用K-means聚类算法的定位误差约为7 cm左右,而没有采用K-means聚类算法排除误差项的平均定位误差约为10 cm左右,因此采用K-means聚类算法排除误差能够提高定位精度。

更直观的来看,目标小车在定位区域中行走,系统界面每隔0.5 s对小车进行一次定位,小车的定位轨迹如图15所示,图中黑色圆形表示定位点,连续定位形成小车的运动轨迹,图中白色圆圈表示辅助节点。

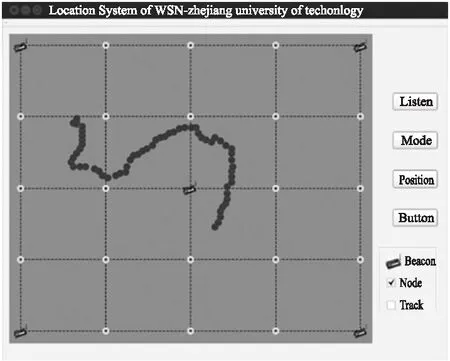
图15 定位系统界面图

定位结果表明小车的轨迹不存在较大幅度的跳动现象,且定位结果连续,因此表明系统对目标小车的定位精度较高,稳定性好。

4 总结

本文实现的基于Zigbee的位置指纹定位方法,该方法在定位区域指纹构建方面与传统的方法有较大的差异,能够基于少量传感器节点快速的构建定位区域的指纹,即使在定位环境发生变化后本文的指纹构建方法也能够快速的重建指纹,从而降低了人工采集的成本,提高了效率。在定位阶段,本文设计了合理的组合匹配方法,该方法能够一定程度的降低室内环境中障碍物对定位精度的影响,具有较好的抗干扰性。最后通过实物实验验证了定位算法在指纹构建方面的快速和准确性,且具有较强的抗障碍物干扰能力,最重要的是定位精度较高。

通过实物实验对算法的各方面进行验证,证明了本文提出的定位算法能够满足实际环境的应用要求,并且在实际应用场景中能够方面快捷的进行定位指纹构建和重建工作,节约了大量的人力物力。