微流体惯性开关用磁流变液流动特性分析*

王铭亮,黄家瀚*,张 崇,沈 腾

(1.宁波大学机械工程与力学学院,浙江 宁波 315211;2.广州大学机械与电气工程学院,广州 510006)

微惯性开关将传感与执行融为一体,直接对加速度信号响应,无需控制开关运动部件的结构装置和驱动源,具有功耗低、响应迅速、灵敏度高、且易微型化和集成化的特点,因此被广泛应用于武器系统、航空航天、惯性导航、通信和汽车等国防和民用领域[1]。然而,普通微惯性开关属于“固-固”接触,接触电极易磨损退化,接触电阻大,且高过载和振动冲击会影响开关的接触稳定性。因此,集成了微流体技术和MEMS加工技术的“固-液”接触型开关(微流体开关)引起了研究人员的广泛关注。

2002年,Kim等人[2]首次提出一种静电驱动水银开关结构,通过驱动电路驱动水银电极移动,从而接通信号电极,实现导通,但该开关结构复杂,所需驱动电压达到100 V～150 V,且引入了电磁干扰;2006年,Shen等人[3]提出了驱动电压更小的静电驱动水银液滴微开关,驱动电压仅为15 V,响应速度可达微秒级;2009年,Sen等人[4]利用电润湿效应驱动水银液滴运动,提出了一种快速接电微开关,响应时间可降至60 μs;以上几种微流体开关结构较复杂,且引入了电磁干扰。2002年,吕苗等人[5]提出了一种水银式微流体惯性开关,当惯性力达到一定阈值时,水银液滴移动并导通电极;2009年,Kim等人[6]设计了一种基于水银液滴的MEMS数字加速度计,可进行0～40 g的加速度测量,该加速度计利用金属液滴水银为运动电极,避免了微机械加速度计的机械疲劳和可靠性问题;2011年,Yoo等人[7]提出了一种基于水银的微惯性开关,当达到阈值时,金属液滴在惯性力的作用下突破被动阀与电极接触,从而实现导通,但是水银液滴在导通后无法恢复到起始位置,只能单次使用;2013年,Kuo等人[8]提出一种基于多壁碳纳米管和水凝胶的微惯性开关,通过L-C谐振器进行传感式导通;2013年Huang等人[9]利用甘油和电容电极设计了一种惯性延时导通开关,可用于武器的延时保险系统中,但是其开关延时时间不能精确控制;2016年,Shen等人[10]提出一种基于镓铟液态金属液滴的微流体惯性开关,该开关在电极接通后可自行恢复,可重复使用。虽然国内外学者对微流体惯性开关做了许多工作,但是依然存在一些问题:开关阈值较小,结构一旦确定,阈值无法调节,只能通过调整开关结构进行调节,且调节范围有限。

针对目前微流体惯性开关阈值较小,阈值无法调节等问题,本文提出了一种基于磁流变液和传感电极的微流体惯性开关,对其阈值特性以及磁场环境下磁流变液滴的速度分布和流动特性进行理论分析,并进行数值模拟和有限元仿真,探讨磁流变液作为微流体惯性开关流动电极的可行性。

1 阀模式下磁流变液流动特性

1.1 理论分析

磁流变液基本工作模式主要有3种:阀模式,剪切模式和挤压模式。阀模式的工作原理示意图如图1(b)所示,使器件的上下极板保持不动,在平行于极板方向的压力作用下,极板间的磁流变液沿极板方向流动,在垂直于极板方向施加磁场,其中的磁性颗粒在磁场作用下形成平行于磁场方向的链状,阻碍了磁流变液在极板间的流动。在该模式下,磁流变液的流动依靠两端的压力差,磁流变液的流变状态可以通过调控所施加磁场的强度来实现自主调节,从而为微流体惯性开关实现阈值可调功能。

为了分析阀模式下阈值大小以及液体流动特性,以惯性力为环境力,对多场耦合下磁流变液的流动进行理论分析,磁流变液流动特性图如1所示。

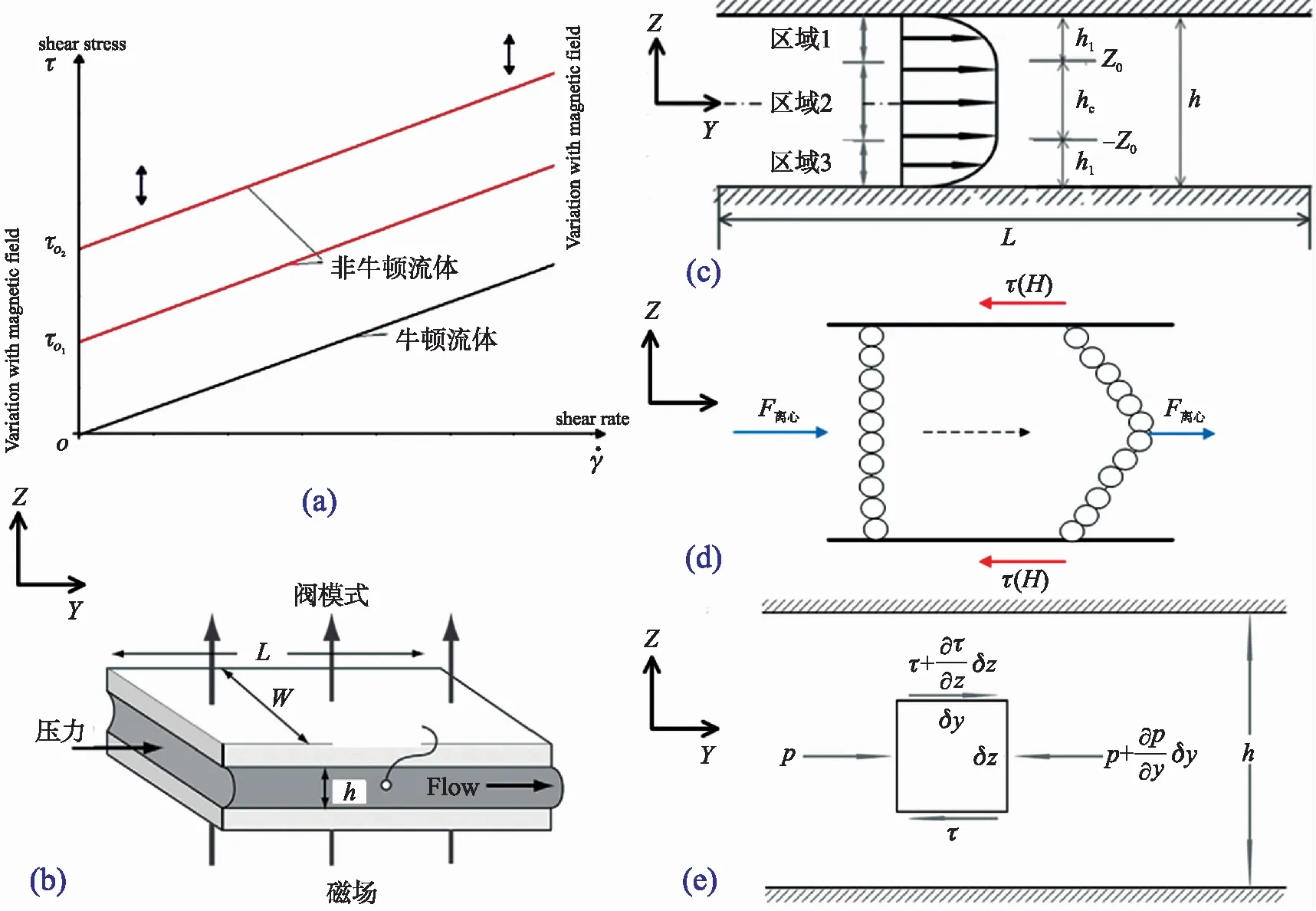
图1 磁流变液特性图

磁流变液在压力驱动下发生流动,当受到外加磁场作用时,其表现为Binghanm塑性体特征,如图1(a)所示,此时其本构方程按下式描述[11]:

(1)

式中:τy(H)是磁流变液的动态屈服应力,随着外加磁场强度H变化,在下文中计算简写为τy。

图1(a)为磁流变液的流变特性,由Bingham模型可知:在不受外加磁场作用时,磁流变液的特性与牛顿流体一致;在受到外加磁场激励下,磁流变液的特性如Bingham流体。当磁流变液所受到的剪切应力超过其屈服应力时,磁流变液的流变特性如不受磁场作用时的粘性流动;反之,则表现为类固体流动。

图1(b)所示为磁流变液阀模式,磁场沿着z方向垂直于上下平板。图1(c)为阀模式下z-y方向上的速度分布图,惯性力沿着y方向。据流变测量学,假设磁流变液在受离心力流动之前y方向的压力梯度∂P/∂y恒定不变,即τ≤τy,那么所受的剪切力分布为:

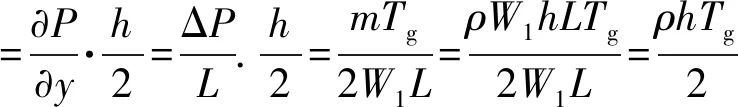
(2)

所以阈值Tg可以表示为:

(3)

动态屈服应力τy可以通过外部磁场进行调节以得到相应的阈值大小。此外,由式(2)可知,平板间的剪切应力与L、W无关。

磁流变液在磁场下呈链状结构,在惯性力作用下,其形态呈弯曲变化,如图1(d)所示。当惯性力大于磁流变液动态屈服应力时,磁流变液在上下平行板间沿y方向流动,取其微元分析,受力如图1(e)所示,

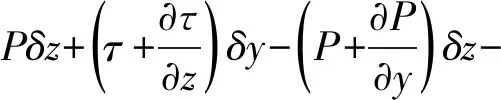
(4)

其中τ为磁流变所受的剪切应力,P为惯性力产生的压强,考虑方向问题,由式(4)可得

(5)

假设磁流变液在受离心力作用下的流动为稳态流动,则压力梯度∂P/∂y恒定不变,那么

(6)

图1(c)所示的速度分布图为磁流变液外加磁场下流经矩形通道的经典分布,由于磁流变液受均匀磁场作用,所以速度分布和剪切分布呈中心对称。速度分布可分为3个区域,区域一(-h/2≤z≤-z0)和区域三(z0≤z≤h/2)为屈服区域,其τ>τy;区域二(-z0≤z≤z0)为欲屈服区域,其τ<τy。

单独对每个区域的速度分布分析,将式(5)代入式(1)可得到速度分布形式

(7)

式中:i代表区域,ai、bi为待定系数,其值的大小与边界有关。

在区域-h/2≤z≤h/2,磁流变液流动成立的边界条件为:

则速度分布可表示为

(8)

根据合理的边界条件,对式(6)进行积分可得

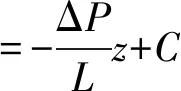
(9)

式中C为常数,其中边界条件为:

τ(h/2)=τ(-h/2)=0,τ(z0)=τy。

所以

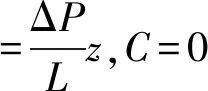
(10)

由式(10)可得

(11)

则中心流的厚度可表示为

(12)

所以速度分布为:

(13)

此时

(14)

因此要使磁流变液得以流动的最小压差ΔPmin可表示为:

(15)

这里注意,式(15)与阈值式(3)结果相同。将式(2)代入式(13)后可得:

(16)

1.2 数值模拟

磁流变液132AD的属性如表1所示,下面以MRF-132AD为例,对阀模式下磁流变液的速度分布进行模拟计算。

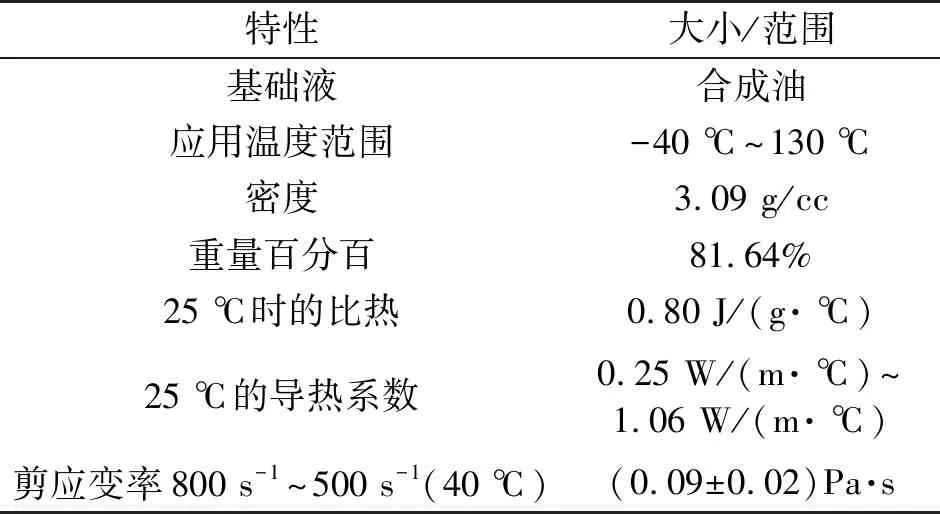
表1 磁流变液MRF-132AD的性能

当磁流变液不受外加磁场作用时,MRF-132AD磁流变液的流变特性类似于牛顿流体,能够顺利通过两个静止或相对移动的圆盘或平板间的缝隙。当施加外加磁场后,在外加磁场作用下,磁流变液的粒子发生磁极化,并在垂直于流动方向组成链状结构,该结构可以承受一定的剪切应力,并阻碍磁流变液在间隙中流动。图2所示的是MRF-132AD磁流变液的屈服特性随所施加的磁场强度的变化规律,从图中可知,增加磁场强度可明显提高磁流变液的屈服应力,当所施加的磁场强度超过200 kAmp/m时,磁流变液的屈服特性受外加磁场的影响较小,达到磁饱和状态。

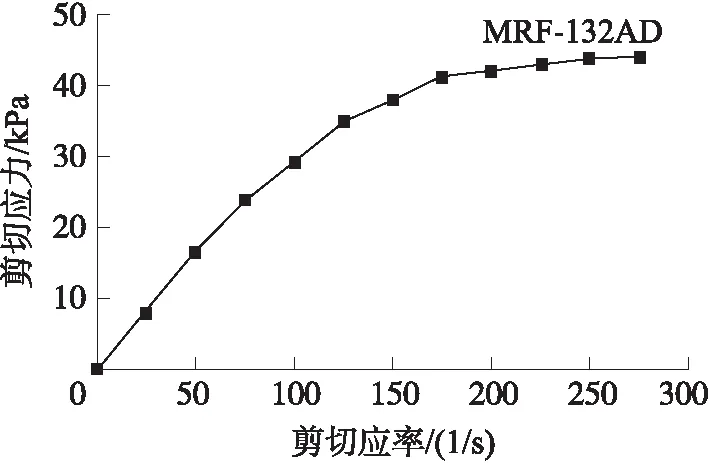
图2 屈服应力与磁场强度的关系(MRF-132AD)

图3所示为阈值随着磁场强度变化曲线图,理论曲线通过式(3)计算所得,曲线为拟合曲线,拟合具体参数在图中已给出,计算中L和h都设定为 1 mm。由图3可以看出,随着磁场强度的增大,磁流变液阀的阈值增大,两者呈正比关系;在0～275 kAmp/m的磁场区间内,阈值的变化范围为0～2 855 g;通过调节磁场强度,利用阈值拟合曲线可以很容易获得所需的阈值大小。

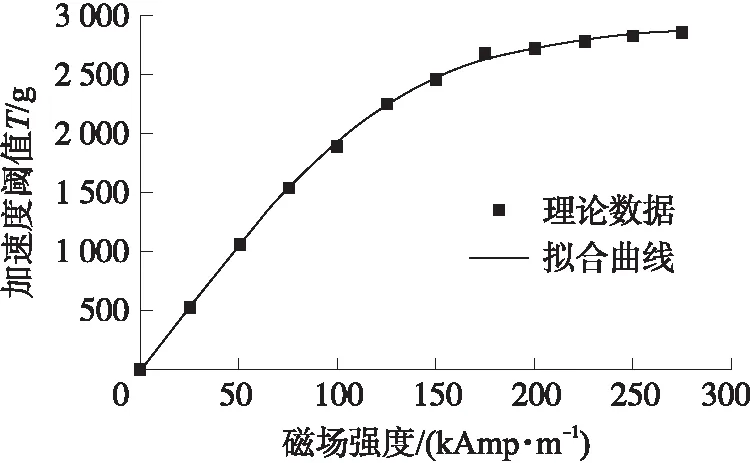
图3 阈值随着磁场强度变化曲线图

此外,利用式(16)可得到磁流变液在平板间的速度分布曲线,如图4所示。计算中采用磁饱和时的屈服应力τHmax=44.112kPa,此时外加磁场H=275kAmp/m,L和h设定为1 mm。利用式(3)得到的液体流动的最小阈值2 855gn,因此计算采用的惯性加速度分别3 500gn、4 000gn、5 000gn、6 000gn和6 500gn。由图4可知,随着惯性加速的增加,流速增大,而中心层厚度逐减小。由此可以证明,当中心层厚度为h时,所得的流动的压差为最小压差,即阀的阈值大小。

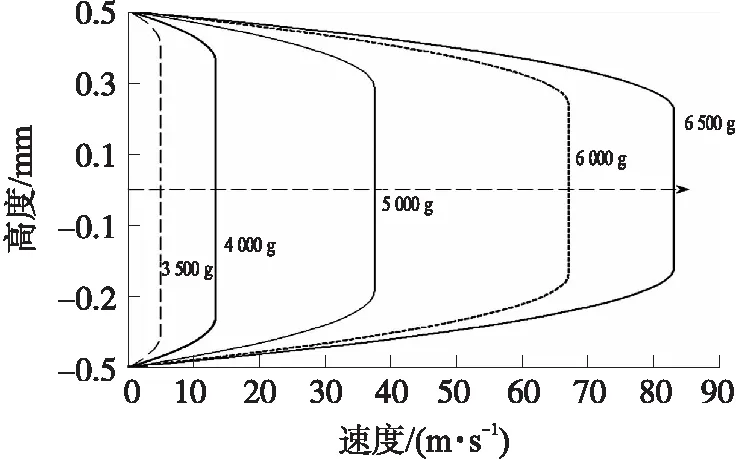
图4 磁场下磁流变液速度分布

2 微通道内磁流变液流动仿真分析

2.1 仿真模型

为进一步验证磁流变液的流变特性,利用有限元分析软件COMSOL MULTIPHYSICS对磁流变液在矩形微通道中的流动特性进行仿真分析,微通道的几何模型如图5所示,仿真所选用的磁流变液型号为MRF-132AD,具体属性如表1所示。

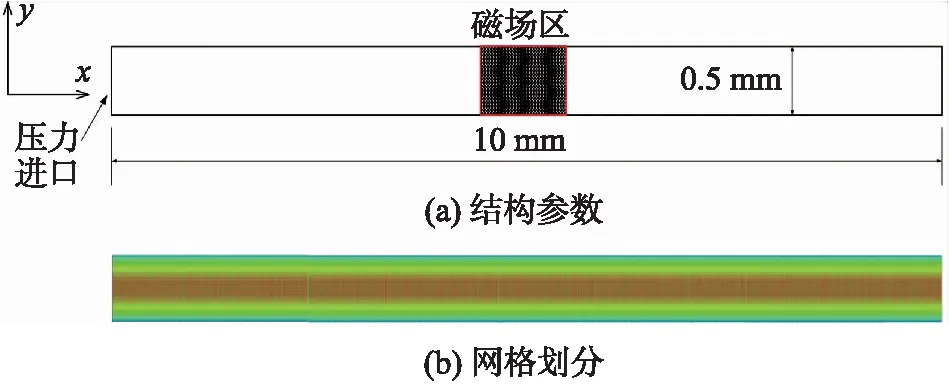
图5 微通道几何模型

为了简化仿真,几何建模采用二维图形,利用压强进口方式考察磁流变液在微通道方向(x方向)的流动变化。图5(a)所示为微通道示意图,其长和宽分别为10 mm和0.5 mm;中间阴影部分为所加磁场区域(1 mm),恒定磁场采用电线圈诱导方式进行施加。图5(b)所示为仿真所划分网格,网格尺寸为0.1 μm,总网格数50 000。

2.2 仿真结果分析

图6所示为不同电流激励下磁场区磁感应强度大小。从图中可以看出,磁感应强度随着电流的增大而增大,当激励电流为0.5 A、0.8 A、1 A和1.5 A时,平均磁场强度分别为0.42 T、0.53 T、0.62 T和0.69 T;整体看来,除了个别位置外,整个磁场较为稳定,磁场区长度接近1 mm。

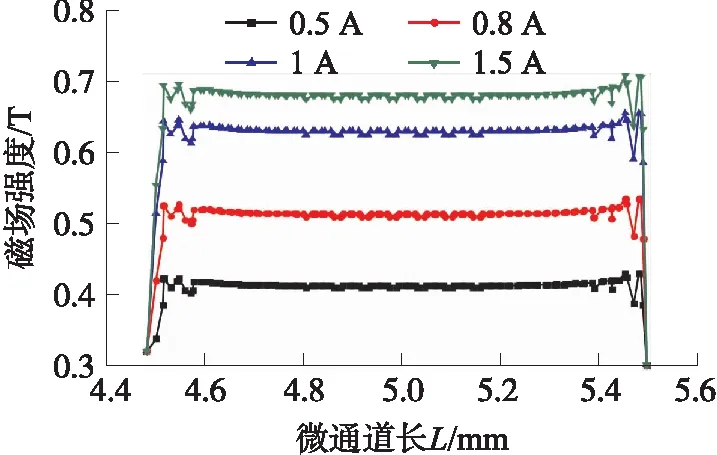
图6 不同电流激励下磁场强度大小

磁流变液在磁场下呈现非牛顿流体状态,其粘度和屈服应力会随着磁场的变化而变化,且具有很大的剪切应力。图7所示为不同磁场下磁流变液在y方向的流速变化,整体看来,流速随着磁场的增大而减小,如当磁场为0.42 T、0.53 T、0.62 T和0.69 T时,微通道内沿y方向的流速分别为0.252 m/s、0.21 m/s、0.153 m/s和151 m/s;由流速曲线可知,磁流变液在微通道中的流速主要由5个部分:①由于进口效应的影响,液体流速由0逐渐增加(-5 mm～-4.5 mm);②当到达一定位置后快速增大并保持不变(-4.5 mm～0.5 mm);③当到达磁场作用区后流速有局部突变(-0.5 mm～0.5 mm);④恢复到原有速度并保持(0.5 mm～4.5 mm);⑤近出口处快速减小(4.5 mm～5 mm)。

图8为磁场处的速度云图,通过观察图7和图8的磁场区流速可以得出:由于磁场的存在,液体流速会出现一段下降变化,最大减小出现在中心位置处(此处磁场最大);随着磁场强度的增大,流速下降率越大,如当磁场为0.42 T、0.53 T、0.62 T和0.69 T时,对应下降率分别为7.8%、9.5%、12.1%和13%。通过对比图7中磁场作用区流速可以得出:磁场越大,屈服应力越大,流速越小,只有当进口压力大于磁流变液的屈服应力时液体才可流动,否则磁流变液变会呈现微阀特性,阻碍液体的传输。

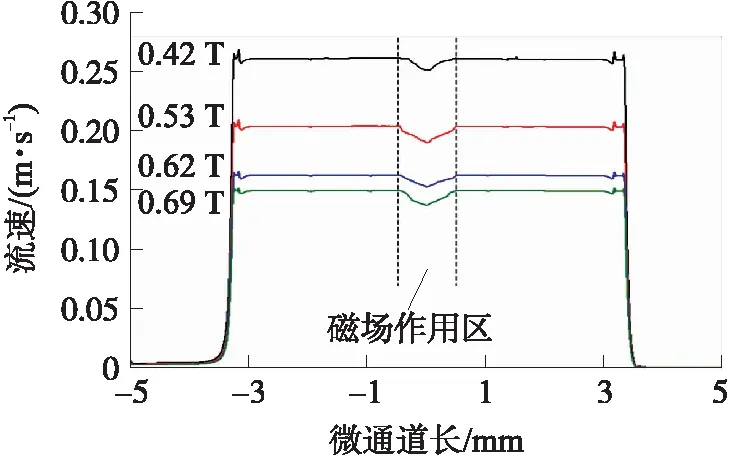
图7 沿y方向流速曲线

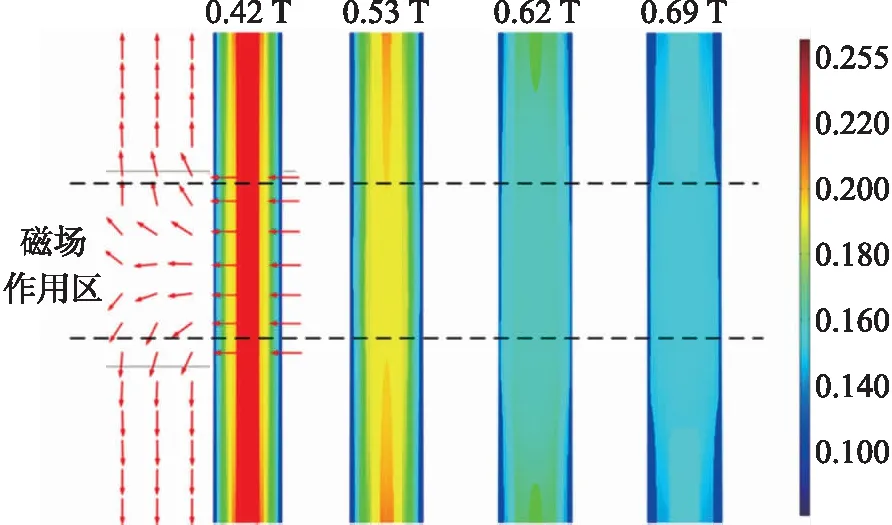
图8 磁场处流速云图

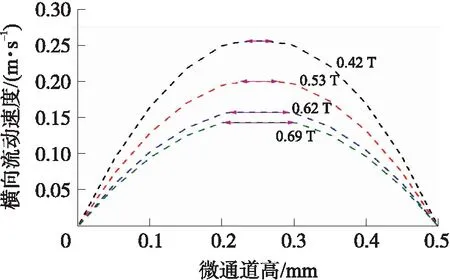
图9 磁场中心位置沿y方向速度分布,箭头所指区域为中心层厚度

图9所示为沿微通道方向5 mm处的y方向横截面速度分布图,图9中箭头所指区域为中心层厚度区。从图9中可以看出,随着磁场强度的增大,流速增大,如当磁场强度为0.42 T、0.53 T、0.62 T和0.69 T时,相应最大流速分别为0.256 m/s、0.203 m/s、0.156 m/s和0.143 m/s。此外,随着磁场强度的增大,中心层厚度也随之增大,此结论和数值模拟结果相同。

综上分析,在零磁场下,磁流变液表现为牛顿流动,流动性能较好;在磁场环境下,其流速会随着磁场的增大而变小,具有作为微阀的功能,并且这种微阀阈值调节方式简单、调节范围广,它只需要控制外围磁场即可获得。

3 结论

本文对阀模式下磁流变液的流动特性进行了分析,构建了磁流变液阀的阈值模型,在此基础上对其流速分布进行了数值模拟,最后,利用COMSOL Multiphysics 有限元分析软件对磁流变液的流动性能进行了仿真。结果表明:磁流变液可为微流体惯性开关提供较宽的阈值调节范围,其阈值可调范围为0～2 855gn,且可通过改变外界磁场强度对其阈值进行调节,无需改变开关结构,阈值调节方式简单。