基于FAVMD-时变峰度的电缆局部放电多传感器在线检测与定位*

2019-04-10师文文郭景蝶

传感技术学报 2019年3期

孙抗,师文文,郭景蝶

(1.河南理工大学电气工程与自动化学院,河南焦作 454000;2.国家电网济源供电公司,河南济源 459000)

电力电缆由于可靠性高,占地面积小,敷设美观等优点,已经在城市、铁路和煤矿等特殊电网中占据极其重要的地位[1-2],但是在其运行过程中,电缆绝缘故障直接影响到电网的运行安全。局部放电(以下简称局放)监测被认为是检测绝缘缺陷发展的最有效手段。电缆局放在线检测与定位技术[3]能及时反映电缆的绝缘状态,提供检修依据,避免电网运行事故的发生,对于保障供电网络可靠运行、实现真正意义上的状态检修具有非常重要的意义。

电磁耦合法[4-5]通过高频电流传感器(HFCT)耦合局放脉冲产生的电磁信号来检测局放信号,不破坏电缆本体,不影响电网运行,是目前最常用的电缆局放在线检测方法。多传感器测量法[6]是一种基于高频电流的行波定位方法,可有效消除波速不定性的影响。但电缆所处环境复杂,通过电磁耦合元件检测到的局放信号受噪声干扰严重,从含噪信号中有效提取局放信号并高精度拾取其初至脉冲是局放故障可靠定位的关键。局放信号提取及初至脉冲拾取方法主要有小波模极大值法、小波包-峰度法、希尔伯特黄变换法HHT(Hibert Huang Transform)和变分模态分解VMD(Variational Mode Decomposition)-Teager能量算子法等。小波和小波包分析对非奇异信号的检测具有良好的效果[7-8],但在算法的实现过程中,需要根据不同的信号,选择合适的小波基和分解尺度,否则会造成局放源定位误差很大。HHT[9]是通过对信号进行经验模态分解EMD(Empirical Mode Decomposition)所得各个基本模态函数中,选取第1个基本模态函数,再进一步进行Hibert变换,在所得频谱中寻找首个突变点,作为局放初至时刻。此类方法存在模态混叠现象,分解所得基本模态可能不是单分量信号,会造成初至脉冲拾取错误。改进算法如EEMD[10]和ELMD[11]算法在一定程度上抑制了模态混叠,但并不能完全消除。VMD分解[12]可将信号无冗余、无疏漏正交的分解到相应的基频带上,文献[13]将其引入到电缆的雷击故障定位中,取得了良好效果,其缺点在于模态数量和惩罚因子等参数的选取对分解的结果影响很大[14-15]。

本文提出一种快速自适应变分模态分解FAVMD(Fast Adaptive VMD),能快速确定自适应分解的模态数量,在保证模态无丢失的同时保证耗时较短,并将其应用于电缆局放信号的提取。结合时变峰度法拾取地下电缆局部放电初至脉冲,通过应用多传感器行波测量法实现强噪声环境下电力电缆局放的可靠定位。

1 问题描述

局部放电在线故障定位时,多传感器测量法通过比较局放信号到达各传感器的时间差实现局放源定位,可有效解决传统单/双端行波法遇到的波速不定性问题。图1为多传感器安装示意图,在电缆本体上安装3个传感器A、B、C,其中A、B位于测量区间的两端,间距为L,C位于AB段中点。随着电缆长度的增加,可适当增加传感器,避免因电缆过长,局放信号沿电缆传播衰减导致传感器无法检测的问题。

图1 多传感器安装示意图

设局放发生时刻为t0,若该局放脉冲到达传感器A、B、C的时刻分别为tA、tB、tC,则易导出局放源距A段的距离为:

(1)

式中:v为局放信号在电缆中的传播速度,可通过记录tA、tB、tC实时求取,过程如下:

若|(tA-t0)-(tC-t0)|<|(tB-t0)-(tC-t0)|,则局放源位于AC段,波速v为:

(2)

若|(tA-t0)-(tC-t0)|>|(tB-t0)-(tC-t0)|,则局放源位于BC段,波速v为:

(3)

由上述分析可以发现,多传感器测量法在进行故障点定位时,不需要事先测定行波波速或使用经验波速,解决了因电缆结构以及信号特征等因素引起的波速不定性问题。但该方法定位精度依赖于局放脉冲初至脉冲的自动拾取精度,从低信噪比信号中有效分离出局放脉冲并可靠提取是此类方法成功实施的关键。

2 基于FAVMD的含噪信号分解

2.1 VMD原理

VMD的核心是变分问题的构造与求解。

2.1.1 变分问题的构造

若每个‘模态’都具有中心频率的有限带宽,则该变分问题就可描述为:在所有模态之和与原信号f相等约束条件下,寻求k个基本模态函数uk(t),而这些基本模态函数的估计带宽之和最小。具体如下:

首先通过Hilbert变换,可以得到各个基本模态函数相应的解析信号和单边频谱:

(4)

其次,为将每个基本模态函数的频谱调制到相应的基频带,把每个基本模态函数加入一个预估中心频率:

(5)

最后通过计算解调信号梯度的平方范数,估计上述每个基本模态函数的带宽,则变分问题表示为:

(6)

式中:uk代表分解得到的第k个基本模态分量;ωk代表uk的频率中心。

2.1.2 变分问题的求解

为将变分问题的约束性转变为非约束性,寻求最优解,引入惩罚因子β和Lagrange乘法算子λ(t),β可保证信号的重构精度,λ(t)可增强约束。Lagrange扩展表达式为:

(7)

(8)

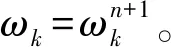
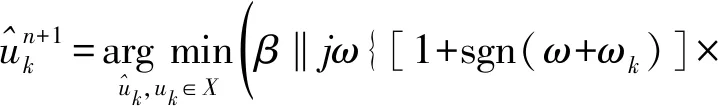
(9)

(10)

此时,可得待求解的二次优化问题解为:

(11)

同理,中心频率取值问题转换到频域上的表达式为:

(12)

由式(12)可得中心频率的更新式为:

(13)

2.2 VMD存在的问题及改进

在进行VMD分解时,若模态数量K设置过小,则分解不彻底,导致模态“混叠”或丢失;K过大,易导致过分解,出现虚假模态。模态数量K的确定目前主要有模态个数波动法[14]和自适应变分模态分解法[15]。模态个数波动法必须先经过人工通过频谱图估计初始值K0,而且在循环过程中,每循环一次,就需要通过频谱图人为判定一次,这样不仅大大增加了计算量,还增加了人为判定的时间,严重影响了在线检测的实时性和智能性。自适应估值法则是从最小K值为2开始循环,直至出现虚假模态结束循环,每次循环都需要进行一次VMD分解,致使计算量骤增,增加运行时间。

针对上述问题,本文提出FAVMD法快速自适应确定VMD最优模态数K值。首先设定一个足够大的模态数量N(一般N≥10),进行VMD分解;将分解得到的各模态与原信号进行相关计算,求取互相关系数ρk;最后统计互相关系数ρk小于阈值a的个数m,则最优K值为:

K=N-m

(14)

综上分析,FAVMD算法流程可表示为:

Step 2n=n+1,执行循环;

Step 6k=k+1,重复步骤2～3,至k=N;

Step 7 根据式(14)确定最优K值;

Step 9 重复步骤2～4,k=k+1,至k=K+1。

3 基于时变峰度的脉冲初至时刻拾取

经FAVMD分离得到的包含局放脉冲的序列中,在脉冲初至时刻,信号的陡峭程度最严重。峰度[16]是基于高阶统计量的一个经典统计量,能够提供比低阶统计量更全面的信息,反映了非对称和非高斯分布时间序列的集中程度,其值大小可以表示信号的陡峭程度。因此采用峰度法进行局部放电初至时刻的精确拾取。

设随机变量为X,p(X)为X的概率密度,则其峰度的定义为:

(15)

式中:mk为随机变量X的k阶统计量。

由式(15)可知,峰度值仅表示了信号整体的陡峭程度,并不能反应时变信号陡峭程度的实时变化情况,需要进一步采用时变峰度算法。

在待检测的离散序列X(i)内,设计以长度为b,采样点i为中心的子时窗,并根据式(15)求取信号在该子时窗内的峰度值,并按下式定义时变峰度值:

(16)

式中:M为X(i)的峰度,M(i)为子时窗的峰度。

在实际应用中,采集到的是关于局放脉冲的稀疏信号,若在全部数据序列上求取时变峰度,不仅耗时,而且数据存储过大。采用时窗能量比方法[17]进行预处理,先确定局放事件发生的时窗[xn],然后在该时窗[xn]内求时变峰度。对于信号时间序列X(i),在时间轴上,以采样点i为中心,在其邻域±l取一时窗,则形成一个以i为中心,长为2l的时窗。后时窗与前时窗的能量比值,即时窗能量比为:

(17)

设定局放事件阈值,通过比较时窗能量比R与该阈值的大小来确定该时窗内是否有局放事件发生。若R小于阈值,则认为该时窗内无局放事件发生,循环至下一时刻;若大于阈值,则确定以该时刻为中心,长为2l的时窗作为局放时窗,通过时变峰度计算拾取局放初至脉冲。

4 实验与结果分析

运用PSCAD/EMTDC中的Bergeron Model电缆模型,配置一根位于地下1 m深,长1 000 m的10 kV单芯电缆,将其简化为四部分:导体、绝缘层、屏蔽层和外保护层,表1为所配置电缆的参数。基于该电缆建立的PSCAD地下电缆局部放电检测系统如图2所示,设定局放故障点距A端100 m,Ea1、Ea2和Ea3分别为HFCT传感器。

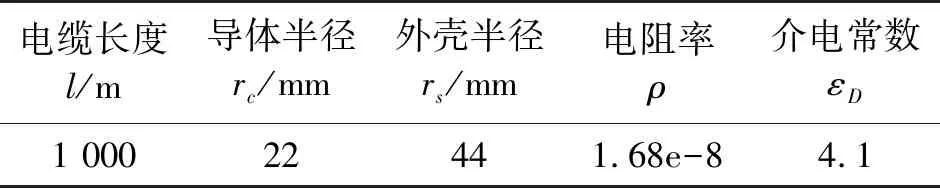
表1 10 kV电缆模型参数

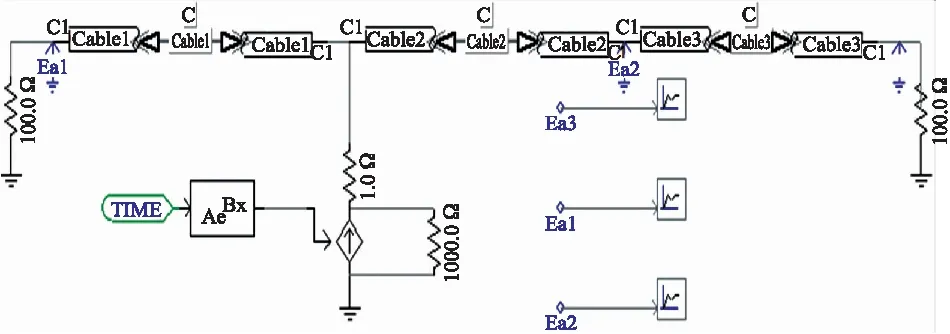
图2 地下电缆局部放电检测系统

局放波形上升沿陡峭,且持续时间极短,可用如下指数函数模型等效:

f(t)=Ae-(t-t0)/τ

(18)

式中:A为局放幅值,t0为局放发生时刻,τ为衰减系数。

4.1 参数选择

在进行VMD分解时,惩罚因子β用于保证信号的重构精度。该值越小,分解所得的基本模态分量带宽越大,导致中心频率出现重叠,造成模态混叠;β越大,带宽越小,但是也增加了过多的计算时间。大量实验表明惩罚因子β在500以内分解所得各模态的相关系数较为稳定,对于如图3所示SNR为-12 dB的含噪局放信号,模态数量取4时,可得模态1相关系数与惩罚因子β之间的关系散点图,如图4所示。由图4可以看出,随着β增加,相关系数先增加后减少,经大量仿真实验验证,当β取12时,相关系数最大,含有信息量最丰富,因此下述实验惩罚因子均为12。

图3 含噪局放信号及其FAVMD分解结果

图4 不同惩罚因子下模态1与原信号的相关系数

相关系数ρ的大小表示信号的相关程度,通常分4个等级,分别为微相关[0,0.3]、实相关[0.3,0.5]、显著相关[0.5,0.8]和高度相关[0.8,1]。在进行FAVMD分解时,ρ用于确定最佳模态数量。对于上述给定的包含4个有效模态的局放信号,不同模态数量下相关系数分布如图5所示,可见,以0.3为阈值时,能判段是否出现虚假模态,因此本文的相关系数阈值a取0.3。

图5 相关系数分布图

4.2 算法的有效性分析

运用时窗能量比方法在包含局放脉冲的含噪信号提取出局放时窗,如图6所示。由于信号含有大量噪声,直接采用时变峰度法无法有效拾取初至时刻。

研究表明,电缆局放所在的频带较宽(最高可达GHz数量级),本文在线检测法采用是应用较为广泛的电磁耦合法,属于高频检测,检测到的信号所在频带较高,而噪声的频谱中主要集中在1 MHz以下。FAVMD可以自适应的分解信号得到K个基本模态分量及相应的中心频率,选取局放信号所处模态,可精确提取局放脉冲并用于故障定位。图7为运用FAVMD分解含噪信号时窗[xn]所得基本模态分量。

图6 包含局放脉冲的含噪信号及局放时窗

图7 基本模态分量

图8 提取局放信号的时变峰度曲线

从图7中可以看出,模态1为局放信号,模态2、3、4为不同频带的噪声信号,与实际检测的局放信号频谱特性一致。运用式(16)计算模态1对应的时变峰度曲线,如图8所示。时变峰度的最大值点为1 250,即局放的初至时刻,与实际值1 251误差仅为1个采样点。出现误差的原因是采样点为离散数据,在[1 250,1 251]内发生局放时,时变峰度急剧减小,离散采样则根据取整原则,默认为1 250最大。在离散数据中,这种误差是不可避免的,只能通过增加采样频率减小误差。

4.3 定位结果及其定量分析

为验证本文提出的算法对强噪声的适应能力,对局放信号添加不同强度的高斯白噪声,分别运用FAVMD-时变峰度法、峰度法[17]及小波包-峰度法[8]进行局放初至时刻的拾取,如图9所示。再运用多传感器测量法对局放源进行定位,所得结果分别如表2所示。

拾取方法信噪比/dBEa1Ea2Ea3误差/相对误差FAVMD—时变峰度法-7-14-161 5261 5251 5251 6031 6021 6031 7311 7311 7310.4 m/0.04%0.8 m/0.08%2.3 m/0.23%峰度法-7-14-161 5262 4952 4951 6032 4952 4951 7292 4952 4952.8 m/0.28%——小波包—峰度法-7-14-161 5251 5252 4951 6021 6022 4951 7311 7322 4950.8 m/0.08%1.9 m0.19%—

由结果可知,在相同噪声环境下,本文提出的FAVMD-时变峰度算法定位精度均优于峰度法和小波包-峰度法。在信噪比为-16 dB的强噪声环境下,FAVMD-时变峰度算法相对定位误差仅为0.23%,而此时峰度法和小波包-峰度法已经无法准确定位。上述实验结果验证了本文提出的基于FAVMD-时变峰度法适应噪声的能力更强,定位精度更高,具有更高的实用价值。

在物理实验方面,研究组在开展该研究之初就规划了物理实验平台,由于设备采购周期较长,目前尚不具备物理实验条件,所以本文未能及时提供相应的物理实验。为了尽早建立物理实验平台,补充物理实验论据,研究组正积极完成科研设备采购申报及论证工作。