一种有向网络目标概率覆盖增强算法*

2019-04-10范兴刚张哲铖王晨浩

传感技术学报 2019年3期

范兴刚,张哲铖,王晨浩,陶俊

(1.浙江工业大学之江学院,浙江绍兴 310023;2.浙江工业大学计算机科学与技术学院,杭州 310023)

如何部署和调度节点,高效实现监控区域内覆盖要求,是有向传感器网络的研究热点之一[1-5]。目标覆盖是用少量的节点实现给定目标的覆盖要求,本文针对有向感知网络的目标覆盖展开研究。有向节点的感知区域不仅和节点的位置有关,也和节点的感知方向密切相关。很多研究者从选择和调整节点感知方向来实现目标覆盖要求。Ai and Abouzeid最先研究了有向网络的目标覆盖问题,选择覆盖最多目标的感知方向,用最少节点实现目标的最大覆盖[6];Shahrokhzadeh B等人基于博弈论研究了目标覆盖,根据目标覆盖贡献和转动能耗,设计节点效能函数,通过最大节点效能函数实现网络寿命最大化[7-8]。如果在随机部署的网络中,有向节点是异构的,有不同的半径,角度和代价,而且不同目标的覆盖要求也不一样。在这种情况下,Zhu等人研究了如何用最小的代价实现不同目标覆盖要求[9]。以上研究都是从固定的和预定义的感知扇区集合中选择提供最大覆盖率的合适扇区。而在文献[10-11]中,节点可以转动到任意方向,Wu等人用最少的节点,较低的能耗实现目标覆盖要求[10]。Jia等人选择具有最大剩余能量的方向组建覆盖集合,实现不同要求的目标覆盖,延长网络寿命[11]。Cai 等人根据目标的权值。选择节点的最优感知方向,实现目标覆盖[12]。

实际上,节点对目标的感知概率随着距离的增大而减少,而且目标感知概率是多个节点联合感知的结果。同时,目标并不一定100%的覆盖才能达到要求,只要达到一定的感知概率,就能满足性能要求。利用概率感知模型研究网络的区域覆盖成为近年的研究热点[13-18]。Zorbas等人在概率感知模型下,通过构建网络的主连通集(CDS),选择目标覆盖集的方法实现目标的概率覆盖[14]。Fan等人利用有向概率感知模型实现了有向节点的概率栅栏覆盖[15]。而关于目标的有向概率覆盖还鲜有研究。作者构建覆盖空洞的修补半径,移动节点在修补圆上选择保持连通的修补位置;增强区域概率覆盖[16]。

在有向概率栅栏覆盖基础上,本文利用节点之间的位置关系,结合联合概率感知,研究如何扩大可用节点选择范围,利用节点的转动能力,实现目标的有向概率覆盖。提出一种基于目标概率覆盖圆的目标增强覆盖方法TarpC(target coverage enhancing scheme based on probabilistic sensing circle)。优化节点感知方向,提高目标概率覆盖率,增大部署效率。

本文余下章节安排如下:第1节描述网络模型。第2节详细介绍基于目标概率覆盖圆的目标增强覆盖方法(TarpC)。第3节通过仿真实验对提出的算法进行性能评估。第4节总结全文并介绍下一步工作。

1 相关模型和定义

要研究有向概率目标覆盖,先给出有向概率感知模型。

定义1有向概率覆盖模型

采用6元组(Pmin,Ls,A0,S,α,θ)表示(如图1所示)。其中Pmin表示概率阈值,当目标点的感知概率大于Pmin时,我们就认为这个目标点可以被完全监测到;Ls=(x,y)表示节点的位置;A0为单个节点的感知区域阈值,在这个区域内的目标都以概率1被感知;S表示单个节点的概率感知区域,在这个区域内的目标感知概率≥Pmin;α表示节点的感知方向;θ为感知角度,在这个角度内的目标能被节点概率感知。

在单个节点的作用下,目标感知概率通过式(1)来计算。其中,d表示传感器与目标t之间的距离,P(d)表示节点对目标的感知概率,λ表示目标与节点连线和感知方向的夹角,μ为感知强度衰减系数。

图1 有向栅栏感知模型

(1)

在图1中目标B,E满足概率覆盖要求。目标C,D初始感知概率小于概率阈值。在概率感知模型下,目标可以被多个节点联合感知的。

定义2目标联合感知概率

在多个节点的综合作用下,目标t感知概率为式(2):

(2)

式中:Sn表示可以感知目标t的所有节点,而Pn(Sn,t)则表示事件t的n个节点的联合检测率,即事件的感知概率。

当目标的联合感知概率Pn(Sn,t)≥Pmin,就称这个目标实现了概率覆盖。

我们研究的问题就是:在感兴趣区域中,随机部署N个有向节点,M个目标,如何利用节点的转动能力,扩大可使用节点范围,使尽可能多的目标实现概率覆盖。

2 目标联合感知概率分析

(3)

给定Pmin可以得到节点的概率感知区域S,再结合感知角度θ可以得到节点概率感知区域S的半径rmin(式(3))。

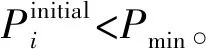
(4)

(5)

定义3目标概率覆盖圆

以目标为圆心,以某个距离为半径画一个圆,圆内任一未覆盖此目标的节点只要调整感知方向,使此目标在其感知角度内,目标的联合感知率就能达到最小感知率要求,则这个圆称为目标概率覆盖圆。

(6)

3 基于概率感知半径的目标覆盖增强算法(TarpC)

由上面的分析可知,对于不满足最小感知概率要求的目标,如果一个节点再对目标贡献感知概率Pd,目标联合感知概率就等于最小感知概率。根据这个原理我们提出一种目标概率覆盖增强算法(TarpC)。

3.1 算法的基本思想

TarpC算法的基本思想如下:运用节点与目标之间的位置关系,选择有效覆盖节点计算目标的初始联合感知概率,得到目标的概率覆盖圆。根据这个概率覆盖圆,增大可使用节点数量,选择最优节点,调整其感知方向,实现目标概率覆盖。

3.2 算法具体过程

TarpC算法伪代码如图2,参数的定义如表1所示。TarpC算法具体步骤如下:

Step1选择覆盖节点集合

计算每个节点的每个感知方向覆盖节点数,为节点选择覆盖目标数最大的感知方向,覆盖目标数大于零的节点为覆盖节点。

Step2计算每个目标的初始感知概率

根据节点和目标的位置关系,计算每个节点对每个目标的感知概率。当对目标的最大感知概率大于最小概率阈值0.3时,此节点标注为覆盖节点,不再转动。否则,标记为不可使用节点。

覆盖节点集合作用下,根据式(2)计算每个目标的初始联合感知概率。

Step3确定目标概率覆盖圆

对于没有满足概率覆盖要求的目标,确定其概率覆盖半径,得到概率覆盖圆。

这个概率覆盖圆内的未使用节点,变为候选可使用节点。

图2 TarpC算法伪代码

参数参数说明M目标集合N1覆盖节点集合N2不可使用节点集合Ri第i个目标的概率覆盖半径Pinitiali第i目标的初始感知概率β节点的目标感知方向Ca目标覆盖率Da部署效率

Step4选择最佳节点

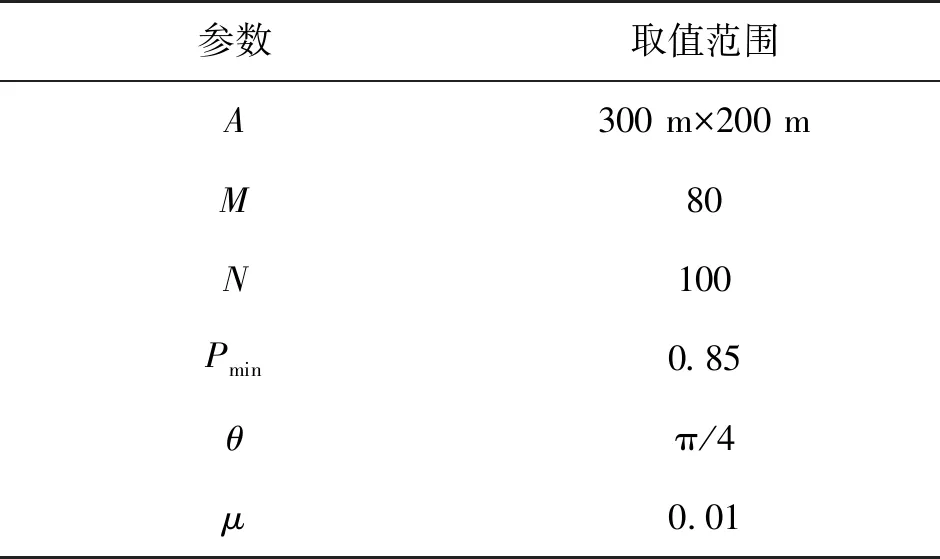
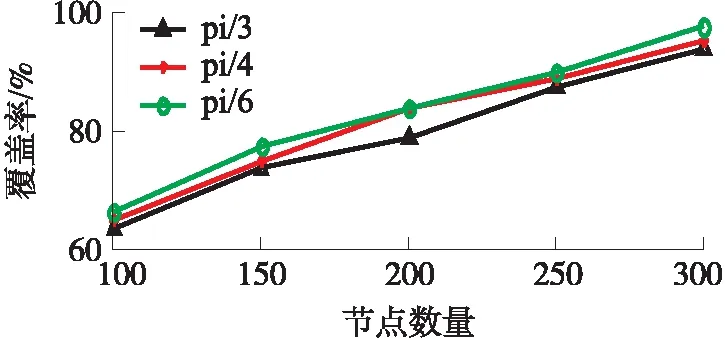
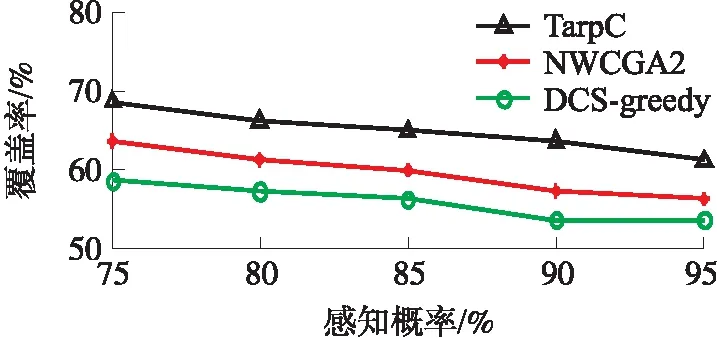
在每个概率覆盖圆内,确定候选可使用节点与目标的距离,选择距离最小的节点转动来增强目标覆盖。如图3中,目标A的概率覆盖半径为R,在这个概率覆盖圆内,有可使用节点B和C,到目标A的距离分别为dB、dC,因为dB

图3 选择最佳节点

Step5确定新覆盖节点目标方向

假设新覆盖节点与目标连线的夹角为β,则唤醒节点的目标方向就是β,如图3中,唤醒节点B的目标感知方向就是β。

图4 节点目标感知方向

3.3 算法的理论分析

假设目标的个数为m,移动节点的数目为N,概率目标覆盖算法时间复杂度为O(m×N)。

由于在目标覆盖的增强过程中,节点只是转动。如果某个目标附近没有节点,可通过联合概率覆盖达到概率覆盖要求,也有可能即使考虑联合概率感知也达不到概率覆盖要求。因此达到概率覆盖要求的目标占总目标的比例即目标覆盖率是反应算法性能的一个关键指标。

随机部署节点实现目标覆盖要求时,只有一小部分节点参与了目标覆盖。这是最小的节点数实现目标覆盖。从另一个角度考虑,能否充分利用已经部署的节点,部署增大目标覆盖。也就是效率问题,参与目标覆盖的节点数在总节点数的比例即为部署效率。部署效率越高,越多的节点参与了目标覆盖,从而减少了节点浪费。即部署效率是反应算法性能的又一个指标。

4 仿真结果

本文运用MATLAB7.0对此算法进行仿真,每组实验数据采用重复50次独立实验取平均值的方式获得。如果没有特别指明,实验的默认参数如表2所示。为了说明算法的性能,我们选用文献[10]的DCS-greedy算法和文献[9]的NWCGA2算法进行性能对比。在DCS-greedy算法中,距离节点越近的目标权值越大,节点选择权值最大的目标实现覆盖。在NWCGA2中,每个节点选择覆盖目标数最多的感知方向,实现目标覆盖。为了一致,这2个算法都选择rmin为节点的感知半径。主要考察目标覆盖率和部署效率两个性能指标。

表2 实验参数

4.1 算法性能

算法本身的性能如图5、图6所示。由于节点仅能够改变感知方向,不能移动改变位置。当节点数较少时,有些目标周围没有节点,仅靠转动不能实现概率目标覆盖。所以,当区域中节点数较少时,目标覆盖率较低只有67%左右。随着总节点数的增加,目标周围的节点数也在增加,通过旋转概率覆盖目标的可选节点增多,目标覆盖率逐渐增加。增大感知角度,根据式(3)节点概率感知半径也相应减少,并不能增大感知面积。所以,同样的目标概率感知阈值下,节点的概率覆盖面积相同,改变感知角度并不能增大目标覆盖成功率。角度变小,覆盖周围的目标数减少。可以使用更多的节点覆盖同样的目标集合,从而提高算法的部署效率。

图5 算法目标覆盖率

图6 算法部署效率

4.2 感知概率阈值的影响

感知概率的影响如图7、图8所示,由有向概率感知模型的特点可知,感知概率阈值越大,单个节点概率感知区域越小,在节点概率感知区域内的目标数越少,对同一个目标的感知概率越小。所以,3种算法的性能都随着感知概率的增大而减少。

图7 概率阈值VS目标覆盖率

图8 概率阈值VS部署效率

对于没有在任何一个节点的概率感知区域内的目标,距离目标较远的节点对这个目标的感知概率

4.3 节点数的影响

节点数的影响如图9、图10所示。随机部署的节点数越多,被覆盖的目标数越多,可使用的节点数越多,所以3个算法的性能随着节点数的增多,目标覆盖率,部署效率逐渐提高。由于DCS-greedy只保证权值最大的目标覆盖,而NWCGA2算法使每个节点覆盖最多的目标。而TarpC算法在覆盖最多目标的基础上,进一步考虑了相邻节点对目标的联合概率感知,一些没有被单个节点概率感知区域覆盖的目标,因为联合感知很有可能达到感知概率阈值要求,从而提高目标覆盖率。同时,尽管有些节点的概率感知区域没有覆盖目标,但很有可能对一些目标有感知概率。所以,相对其他2种算法,TarpC算法具有较好的目标覆盖率和部署效率。