基于波数域上Fourier变换的磁异常信号处理

郑建拥,范红波*,尹 刚,李志宁

(1.陆军工程大学石家庄校区,石家庄 050003;2.中国空气动力研究与发展中心高速所,四川 绵阳 621000)

在地球物理学领域里,Fourier变换是一种常用的数据处理方式,在不同的研究方向上,都有很深的研究潜力。如Nabighian(1972,1984),Nabighian and Hansen(2001),Nelson(1986)[1-3]利用Fourier变换在磁场的水平和垂直分量之间进行转换;Nelson(1988)[4-5]计算了总磁场异常的磁梯度张量;Lourenco和Morrison(1973)[6]描述了磁总场模量(TMI)和磁场矢量分量之间转换的数学推导;Mohan,Sundararajan和Seshagiri Rao(1982)[7]利用Fourier变换建立地质框架;Sundararajan和Srinivas(1996)[8-9]提出内禀磁标势方法以及在地震上的应用。(Hood,1980;Overton,1980)[10]也做过关于地球物理应用的磁梯度张量数据的分析工作。目前在磁异常正演领域,在数据的时间域和频率域分析上都有成熟的推导理论,但这些理论也仅限于磁异常数据正演,实际应用上并无巨大突破,也尚未涉及波数域的推演。而且在磁异常信号预处理方面,并没有成熟的方法或者研究的思路、方向。

传统的地磁勘测,是通过标量磁力仪采集地磁总场强度的值,即磁总场模量(TMI),所含信息量比较少,且信号质量也不高。而近些年磁通门传感器和超导量子干涉器件得到一系列新发展,可以直接测量磁场矢量及其空间变化率;全张量磁力梯度仪系统可以测量所有线性独立梯度张量分量,也即磁场分量的一阶导数。因此所得到的磁异常信息的质量和数量得到很大改善,精确度明显提高。而且磁性目标产生的总场、矢量场、总场梯度和梯度张量场在空间域中的计算方法已经非常成熟。但以上途径的数据处理过程都是根据不同仪器的测量方式,利用简单的空间上的差分或求和来完成TMI、磁场矢量和梯度张量之间的变换,实际应用上存在很大的误差。因此,有必要运用数学方法推导TMI、磁梯度张量和磁场矢量等之间的解析关系,系统地进行各量之间的转换。基于此,在Nabighian等人所做的数学框架的基础上,提出了利用波数域上的Fourier变换,推导TMI、磁场矢量和磁梯度张量相互之间关系的方法。并在实验数据上填充反距离加权插值算法,得到了噪声更小、更清晰、分辨率更高的磁异常数据,有利于之后的磁异常信号的解释和应用。

1 空间域的推导

在空间域数据中做频谱分析,即可得到波数域数据。因此需要先得原始空间域数据。式(1)为传统空间域上磁标量φ、磁场矢量三分量(Bx、By、Bz)和磁梯度张量矩阵G三者的关系公式,而式(2)为从磁场矢量推导磁总场模量(TMI)的求解公式(公式中表示为Bt)[11-14]

(1)

(2)

图1所示的4磁通门十字形阵列探测仪是较为普遍的地磁测量设备,除此外还有长方形阵列、四面体阵列等根据不同需要和算法设计的仪器。除磁通门外,还有超导量子干涉仪等精度更高的地磁测量仪器[15-20]。

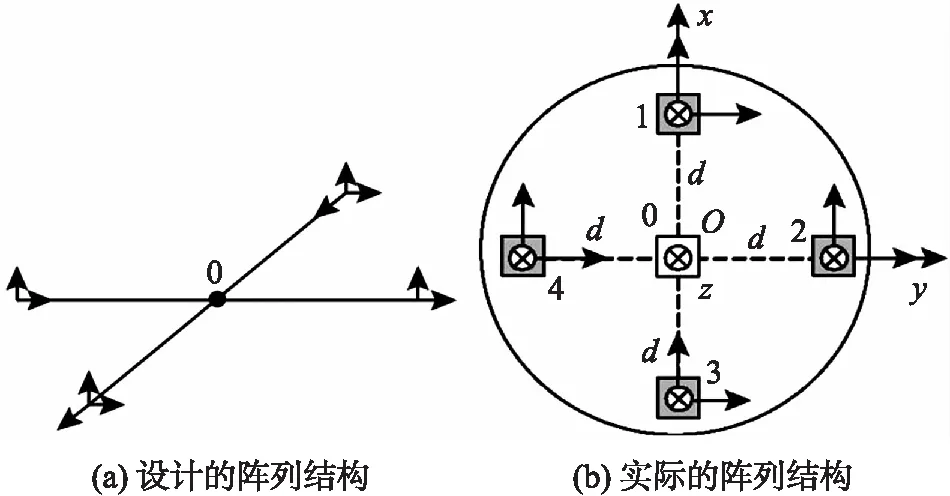
图1 实验测量设备

磁通门直接测量的仅为磁场矢量三分量(Bx、By、Bz),可以根据式(2)求解出磁总场模量(TMI)。而磁梯度张量的算法,是根据磁通门摆放位置的不同而差分计算得来的。以图1的阵列为例,磁梯度张量矩阵G的计算公式如下[11]:

(3)

Bij(i=1,2,3,4;j=x,y,z)表示第i个传感器在j方向上的磁场矢量;d为基线距离。

可知,空间域上实际磁异常数据的测量和磁梯度张量数据的计算受仪器设备的影响比较大,推导计算过程本身存在一定的误差,如基线的选取、4个传感器的对称对中,以及数据计算方法等因素不可避免的产生了误差。

2 波数域的推导

波数域方法首先对探测得到空间域数据进行频谱分析(一般为傅里叶变换)后,在波数域上推导磁异常数据各种量的解析关系式,然后利用逆傅里叶变换得到磁异常数据。相对于直接从空间域得来的数据,其优点是异常频谱表达式较为简洁紧凑,计算效率更高。

磁场矢量是磁标量φ=φ(x,y,z)的负梯度,而磁场梯度张量元素是磁标量φ的二次导数[6]:

(4)

式(5)是空间域磁标量的傅里叶变换公式:

(5)

二维表示磁标量的逆傅里叶变换:

在这里,把这两种变换缩写为:

φ(p,q)=FT{φ(x,y)}
φ(x,y)=FT-1{φ(p,q)}

(6)

式中:p和q为水平波数。

二维傅立叶变换的使用要求将测量的数据采样到规则的空间平面。因此,积分平面被限制为垂直坐标为常数的某一平面。

对于平面的垂直梯度张量Gkz[3],计算方法见式(7):

(7)

这是在波数域中,由磁场矢量推导垂直方向的梯度张量Gkz的公式。其傅立叶变换展开如式(8):

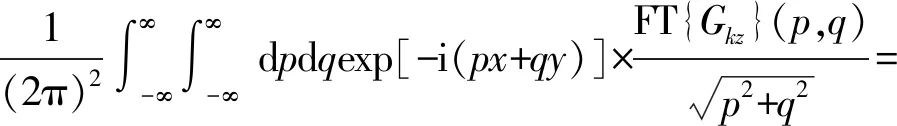
(8)

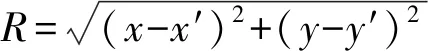
(9)

联立式(7)～式(9)可以得到波数域的垂直梯度张量公式。以上这些关系可用于磁梯度垂直张量Gkz和磁矢量三分量Bk之间的变换。

为了获得水平张量公式,有必要考虑波数域中的水平导数:

FT{Gkx}=ipFT{Bk}

(10)

FT{Gky}=iqFT{Bk}

(11)

(12)

把式(7)、式(10)、式(11)代入式(12),可得波数域上的磁梯度全张量公式[3]:

(13)

联立式(8)、式(13)可以在波数域上建立起磁场矢量三分量和所有磁梯度张量之间的解析推导。

还可以把式(13)重新定义为下式[4-5]:

FT{Bx}=FT{-∂φ/∂x}=-ipFT{φ}
FT{By}=FT{-∂φ/∂y}=-iqFT{φ}
FT{Bz}=FT{-∂φ/∂z}=-rFT{φ}

(14)

(15)

(16)

将此式整理为FT{φ}的形式,然后代入到式(14),可以得到TMI和磁场矢量三分量在波数域上的关系:

(17)

至此,完成在波数域上TMI、磁场矢量和磁梯度张量相互关系的解析公式推导。

3 插值处理

通过测量平面上的垂直或水平的磁场矢量,可以计算出梯度张量。利用张量梯度代替总场或者矢量场的优势在于张量分量不是地球磁场方向的函数,所以数据的等高线不会受到总场或垂直梯度所造成的倾斜问题。因此,张量梯度可以更容易解释或增强从全域中获得的信息。计算张量分量的信噪比本质上是原始磁场矢量测量的信噪比。但是在信号转换计算过程中,高频噪声会被加强,且TMI转换为梯度张量时对噪声的放大作用,远大于矢量场转换为梯度张量,因此在转换过程中,需要进行消噪处理。同时还应该要注意数据网格的间距,数据点的总个数除以网格间距决定了二维数字傅里叶变换中的分辨率。

因此,使用反距离加权算法(IDWA)对数据圆滑网格化处理。IDWA计算一个格网结点时给予一个特定数据点的权值,权值与指定方向的结点到观测点的距离的倒数成比例,较近的数据点被给定一个较高的权值[4-5],同时在此过程中,数据的高频噪声得到抑制,数据等高线的边界更加柔和,消除了数据点的畸变。

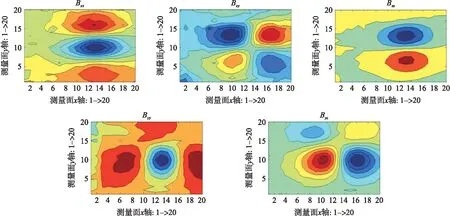
图3 空间域梯度张量

由于基于FFT的算法在波数域中是离散化的,采样点之间数据连续性可以通过以下过程自动实现。一般来说,在应用波数域中的任何转换之前,输入数据网格必须以特殊的方式进行处理[15]。采用的方法是将减去了所有线性二维趋势的数据扩展到具有2N个点的方阵,并采用反距离加权算法处理,使其与常规数据保持一定距离,以确保满足FFT算法要求的连续性和周期性边界条件。这些预处理措施可以快速准确地计算网格。在对变换后的数据进行逆傅里叶变换后,将被移除的线性趋势解析后添加到输出里。为了将TMI转换成磁场矢量,将减去的趋势与地磁背景场方向矢量的相应分量相乘并添加到结果中。最后一步,对于磁梯度张量的垂直和整体积分,将水平梯度的傅里叶变换除以算子核p和q后进行高通滤波。这可以消除由于合并而在相邻网格边缘的磁异常上产生的人为影响,最后简单地加上地磁背景场的绝对值。

4 实验分析

基于图1和图2所示的磁异常信号探测设备,设计了相对应的实验。以验证上述方法对磁异常信号的预处理作用。

实验测量了直径15 cm,长1.2 m的铁圆柱在2 m的埋深下,其正上方20×20个点的水平测量面的磁异常数据。如图2所示的正方形实验台,边长两米,每隔0.1 m设置一个测量点,通过横纵移动磁通门传感器测量每个点的矢量三分量。再分别利用空间域和本文提出的波数域两种方法,由磁通门测得的磁矢量场信号计算出TMI和梯度张量信号,分别画出相应的磁异常信号的等高线图,比较两种方法所计算得到的信号的质量和效用。

图2 实验测量台

图3为空间域方法计算所得的5个独立张量元素[11-13](Bxx、Bxy、Bxz、Byy、Byz)的等高线图。

图4为利用本文提出的波数域方法得到的相应5个元素。图5中,(a)为空间域上计算所得的TMI,(b)则是在波数域上计算所得的TMI。很明显可见,磁异常数据中高频噪声被抑制,图形块边缘的畸变点得到柔和处理。数据的整体层次分布更加简洁明显。更加方便从中提取目标形状和位置特征信息。相比于图3和图5(a),图4和图5(b)磁场的特征更加明显,并且结合了磁梯度张量分量的两个特征:低噪声水平和与磁通门读出的磁场矢量分量相比的更清晰的磁场描述。由于叠加的水平梯度张量分量增加了它们对降低磁场矢量分量产生的噪声水平的贡献,所以水平波数p和q的分割具有更低的噪声,因此图中显示的边界更加柔和,特征更加突出,条纹条理更加清晰。

而在波数域上积分的另一个优点是它突出了更短的波长细节,并且可以通过快速傅立叶变换算法(例如,在MATLAB中)快速执行。因此,在波数域上积分比在空间域中更加准确和方便。

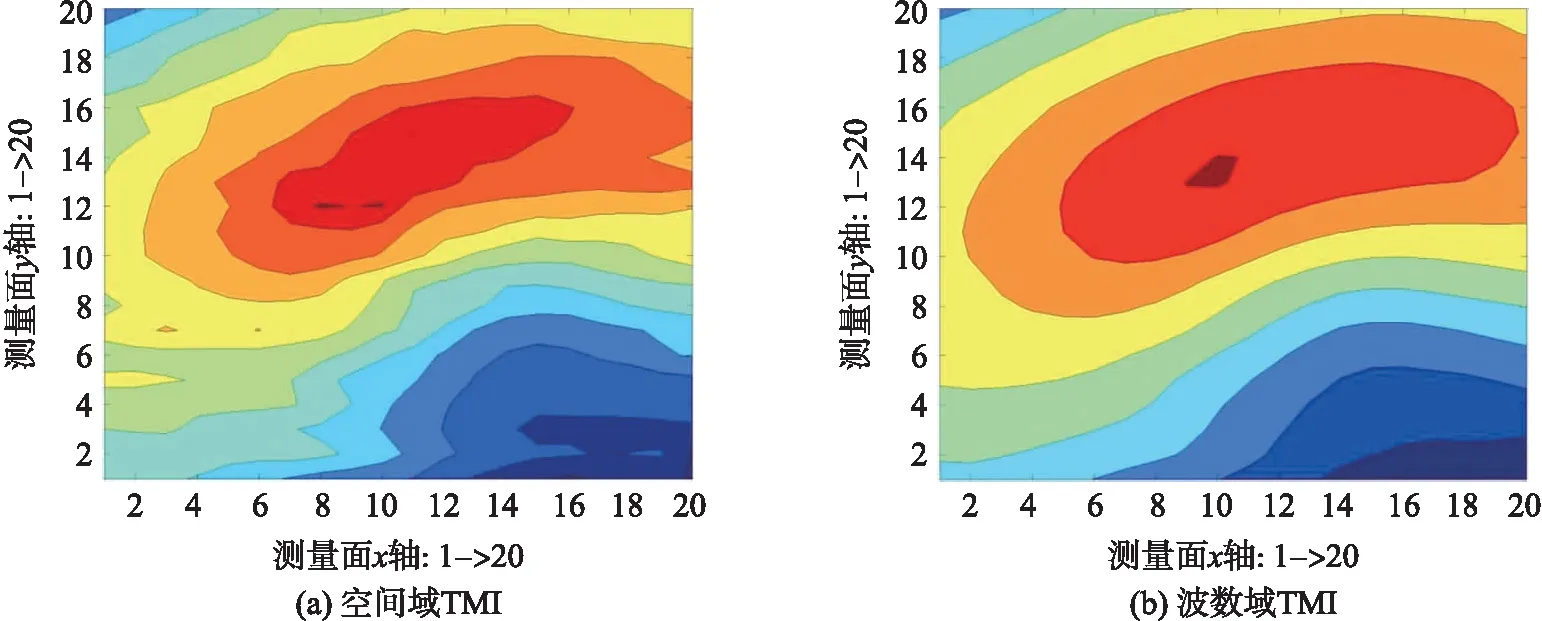
图5 空间域和波数域TMI

5 结论

本文提出了在波数域上利用Fourier变换,计算推导TMI、磁场矢量和梯度张量三者关系的方法,并结合反距离加权插值算法,对磁通门所测量的的磁场矢量数据进行了预处理,较为准确地计算出了磁性目标的张量信号,并在一定程度上抑制了噪声,证明了波数域上计算的可行性。相比于传统的空间域上得计算方法,波数域所计算的梯度张量信号质量更高、边界更清晰、噪音更小。

证明了可以通过对某类测量系统采集的信号进行适当的数据处理,然后通过波数域的推导计算得到高质量和空间分辨率的另一形式的磁信号。并且这种转换是双向的,我们可以从磁场矢量中得到磁梯度张量,反之亦然。