遗传算法的多参数自适应随机共振低浓度气体检测*

亢艳芹,刘 进

(安徽工程大学计算机与信息学院,安徽 芜湖 241000)

因低浓度气体信号微弱,容易被噪声淹没,使得检测受限,测量精度往往难以达到预期。近年来越来越多的新技术被用来检测低浓度气体,例如光腔衰荡测量技术、超声波技术以及光干涉原理等,但这些方法大多很难消除系统固有噪声,并且去噪过程中会损害有用信号,测量仪器受环境干扰大。而随机共振理论的发展及其在微弱信号检测领域中的广泛应用,为低浓度气体检测提供了新思路。随机共振的基本思想是利用噪声增强微弱信号中的有效特征信息,从而将淹没在强噪声背景中的有用信号提取出来,是微弱信号检测和处理领域中的研究热点[1-4]。

随机共振包括非线性系统、输入信号和噪声三要素,只有当这三者之间存在匹配关系时,才会产生随机共振现象,系统输出信噪比得到提高。对某一确定的被测信号,常用方法是添加适量噪声从而改变噪声强度实现共振,但这种方法处理效率低,共振不明显[5]。随着研究的不断深入,人们发现,相比改变噪声强度,调节系统参数的方法能够使系统更好实现共振,因此,参数调节随机共振成为微弱信号检测领域的一个重要研究方向[6-7]。如,Huang等人采用调节某一参数而固定其他参数的方法,使随机共振系统达到共振状态,实现了传感器的故障信号检测[8]。Luo等人提出了一种参数调节随机共振算法,即不改变噪声强度,调节两个系统参数得到最优值,使系统产生了随机共振现象[9]。遗传算法是一种通过模拟生物遗传选择和进化过程不断逼近最优解的概率搜索算法,为此,利用遗传算法来调节和优化随机共振系统参数的方法成为一个新的研究方向。例如,Wang等人以周期信号为研究对象,采用遗传算法优化随机共振两个系统参数得到最优值,仿真实验表明了该方法对小参数和大参数信号均适用[10]。Zhang等人设计了一种自适应随机共振,选用遗传算法并行优化两个系统参数,实现了最佳共振效应[11]。与此同时,Lu等人结合最优化理论,将随机共振的两个系统参数和噪声强度作为约束条件,以互相关系数为目标函数,从理论上证明了此目标函数存在唯一全局最大值,并且此最大值要比单独调节噪声强度或系统参数时的值要大[12]。这些研究都为随机共振系统的多参数优化方法奠定了理论基础。由于随机共振系统的多个参数之间相互制约,相互影响,以单个或者某两个参数作为优化对象会忽略多个参数之间的协同关系,难以使系统达到最优共振状态,限制了随机共振技术在工程信号检测中的广泛应用。因此,如何同步优化多个参数使系统实现最佳共振,成为随机共振在微弱信号检测领域研究的核心问题。

结合最优化理论,本文提出一种基于遗传算法的多参数同步优化自适应随机共振系统,并将其应用于低浓度气体检测中。该方法首先对原始低浓度气体响应信号进行预处理,然后以系统输出信噪比为优化目标函数,利用遗传算法对随机共振的两个系统参数和噪声强度进行自适应并行优化,获得最优随机共振系统,最后将预处理后的低浓度气体信号作为输入信号进行最优共振处理。本文实验实现了低浓度氨气(NH3)的检测,并且与传统的参数调节随机共振相比,共振效果更明显。

1 自适应随机共振的低浓度气体检测方法

1.1 双稳态随机共振理论

双稳态非线性系统的郎之万方程可以描述为[13]:

(1)

式中x(t)为系统输出信号,s(t)为系统的输入信号,ξ(t)为均值为零方差为1的高斯白噪声,D为噪声强度。V(x)为该系统的势函数,定义为:

(2)

则非线性郎之万方程可以表示为:

(3)

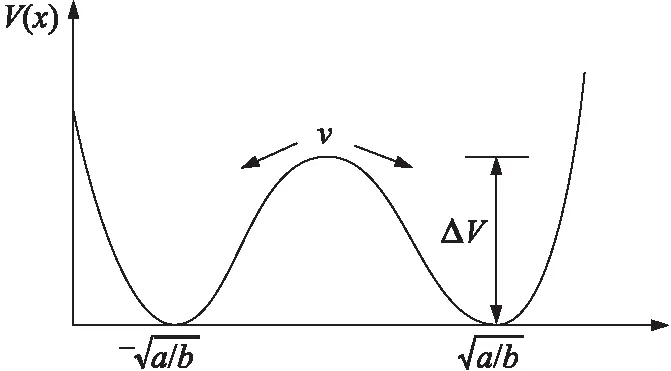
图1 非线性双稳态系统势函数

(4)

1.2 非周期气体信号的预处理

随机共振模型的输入信号要求是小参数信号,即信号频率、信号幅值和噪声强度都远小于1[14-15]。实际应用中采集的原始低浓度气体响应信号一般是非周期信号,其频率分布不是集中在一个或者某几个确定的频率上,而是分布在具有一定宽度的频域内,无法实现系统评价指标SNR的计算。因此,在随机共振处理之前,需要对反映气体浓度的原始信号数据进行预处理,使其符合系统要求。图2为预处理流程图,具体步骤如下:

①获取气敏传感器对目标检测气体的电阻响应r(t),并对r(t)进行归一化处理:y(t)=(r(t)-rmin)/(rmax-rmin),式中rmin和rmax分别是r(t)的最小值和最大值;之后按照相同的时间间隔进行采样得到一系列信号R(t)=(R1,R2,R3,…Rn),Rn为气敏传感器的电阻响应信号;

②利用载波信号c(t)=A0sin(2πfct)对R(t)进行调制,得到对应的周期信号s(t)=R(t)c(t)=R(t)A0sin(2πfct);

③将s(t)作为系统输入信号并与叠加的噪声n(t)一起输入到随机共振系统中。

图2 非周期气体信号预处理流程图

1.3 遗传算法的自适应随机共振多参数优化

本文以系统输出SNR作为适应度函数,并利用遗传算法对随机共振的系统参数a、b和噪声强度D进行自适应同步优化,最终构建最优随机共振系统。图3为遗传算法确定最优参数的基本流程图。

图3 遗传算法确定系统最优参数流程图

具体步骤如下:

①编码:首先定义参数a、b、D的搜索区间和精度,设a∈[amin,amax],b∈[bmin,bmax],D∈{Dmin,Dmax],精度为e;然后根据搜索区间和精度,分别计算参数a、b、D对应的编码长度la、lb、lD,即:

(5)

最后对其进行二进制联合编码,得到对应的码字clacla-1cla-2…c1、dlbdlb-1dlb-2…d1和plDplD-1plD-2…p1;

②种群初始化:设定种群的规模,之后随机选取个体组成一个初始种群;

③解码:对步骤①中编码的个体进行解码,得到对应的系统参数a、b、D。解码公式为:

(6)

④适应度评价:本文选择系统输出SNR作为适应度函数,即SNR=f(a,b,D),根据式(4)进行适应度函数的计算,将步骤3)中解码得到的每个个体对应的系统参数a、b和噪声强度D,代入随机共振系统中,计算SNR,即个体的适应度值;

⑤选择交叉和变异:根据步骤④中获取的个体适应度值,采用赌轮模型进行优良个体的选择,并通过交叉、变异和倒位操作逐渐形成新一代种群;

⑥终止:重复步骤③～步骤⑤,当达到预先设定的迭代次数时,循环终止(本文中设定的迭代次数为50次),此时系统SNR的最大值所对应的系统参数a、b和噪声强度D即为当前最优参数。

1.4 基于遗传算法随机共振的低浓度气体检测系统

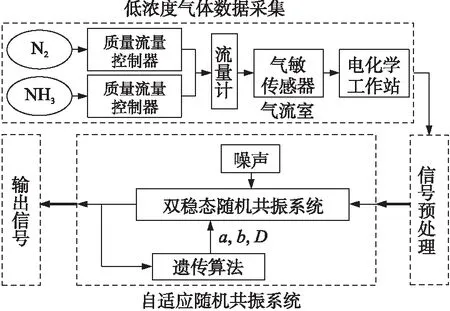
图4 自适应随机共振的低浓度气体检测系统框图

图4为自适应随机共振的低浓度气体检测系统。该系统包括低浓度气体数据采集模块、信号预处理模块和自适应随机共振系统模块。其中,数据采集模块中,高纯氮气(N2)是载气,氨气(NH3)是目标检测气体,所需待测气体的浓度可通过调节气体质量流量控制器得到,气敏传感器的电阻响应可通过电化学工作站实时读取和记录。采集的原始电阻信号需要先按照1.2节所述方法进行预处理,并输入随机共振系统中;然后,利用1.3节所述遗传算法,对系统参数a、b和噪声强度D进行自适应同步优化,得到最优参数a、b、D和最优的随机共振系统,最后,输出共振后的响应信号。

2 实验及结果

2.1 数值仿真实验

构造一周期信号s(t)=Asin(2πf0t),频率f0=0.1 Hz,幅值A=0.5,如图5(a)、5(b)所示。本实验中采样频率fs=5 Hz,随机共振系统参数的搜索区间分别为:a∈[0.1,6],b∈[0.1,6],D∈[1,10],精度e=10-4。将信号s(t)输入本文所提出的自适应随机共振系统中,采用SNR作为适应度函数,得到最优参数aopt=0.618 0,bopt=1.503 4,Dopt=1.914 0,系统输出信号的SNR最大值为SNRmax=-23.671 4 dB。仿真结果如图5(c)、5(d)所示。

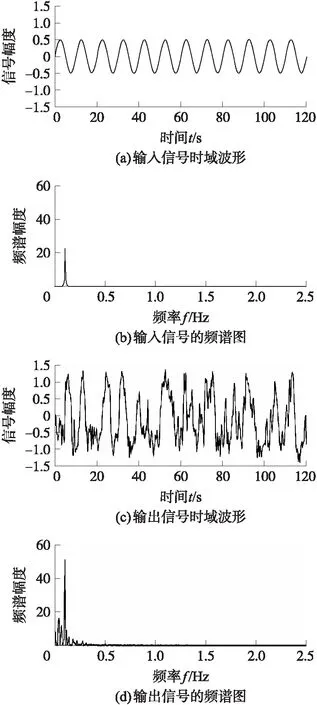
图5 输入信号和系统输出信号的时频图

由图5(c)可以看出,输出信号时域波形较好的恢复出了输入信号的周期成分。与图5(b)相比,图5(d)中在输入信号频率f0=0.1 Hz处频谱峰值显著增大,谱线也很清晰,说明该方法能使系统产生明显的随机共振效应,可以高效实现微弱信号检测。

2.2 低浓度气体检测实验

实验环境:室温是20 ℃、标准大气压、空气相对湿度是70%,传感器是采用介电泳技术制备PEDOT/PSS-SWCNTs气敏传感器[16]。

在实验前,首先向气流室通入一段时间N2直至气敏传感器的电阻值达到稳定状态,之后通入3×10-9NH3,并使用电化学工作站实时读取和记录气敏传感器的电阻响应。为了减少数据采集的误差,实验重复进行3次,计算出平均值作为3×10-9NH3的电阻响应。然后再通入3×10-9NH3,依次按照前面的操作步骤可以得到浓度为6×10-9的NH3电阻响应,接下来以每次2×10-9的浓度向气流室通入NH3,可以得到浓度为12×10-9、18×10-9、24×10-9、40×10-9等浓度的NH3电阻响应。实验选取6种不同浓度待测NH3,其电阻响应经归一化处理后的电阻-时间曲线如图6所示。

图6 6种不同浓度NH3归一化后传感器响应图

图7为6种浓度NH3的原始电阻信号经预处理后的频谱图。其中,数据长度N=620,载波信号幅值A0=1,载波信号频率fc=0.1 Hz,采样频率fs=5 Hz。首先将预处理后的3×10-9NH3电阻信号,输入到传统的参数调节随机共振系统中[17],设定系统参数的寻优范围a∈[1,5],b∈[1,9],搜索步长ia=ib=0.1,噪声强度D=1.2,采用SNR作为评价指标,通过遍历搜索,得到当前最佳系统参数aopt=2.2,bopt=3.3,并构建随机共振系统。然后将预处理后的其他浓度NH3电阻信号,输入已构建好的随机共振系统中,其输出信号的频谱如图8所示。从图中可以看出,与图7的输入信号频谱相比,图8中6种不同浓度的NH3信号频谱在输入信号频率fc=0.1 Hz处的频谱值均有所增大,出现了随机共振效应。

图7 6种不同浓度NH3的电阻信号经预处理后的频谱

图8 参数调节随机共振系统输出信号频谱图

现用本文所提出的基于遗传算法的自适应随机共振系统对上述6种不同浓度待测NH3进行处理。首先将预处理后的3×10-9NH3电阻信号,输入自适应随机共振系统中。设定参数a、b、D的搜索区间均是[0.1,10],精度e=10-4,编码长度l要满足l≥17。以SNR作为适应度函数,通过遗传算法的选择交叉变异等环节对参数a、b、D进行自适应同步优化,得到最优参数aopt=0.550 6,bopt=0.757 9,Dopt=2.408 7,并构建最优随机共振系统。接下来分别将预处理后的6×10-9,12×10-9,18×10-9,24×10-9,40×10-9的NH3电阻信号,输入已构建好的最优随机共振系统中,6种浓度NH3电阻信号经随机共振处理后的频谱如图9所示。和图7共振处理之前的信号频谱相比,图9中,6种不同浓度NH3电阻信号经最优随机共振处理后,输出频谱在输入信号频率fc=0.1 Hz处的频谱峰值均显著增大,并且都非常突出,共振谱线也很清晰,说明该系统产生了明显的随机共振现象。与图8参数调节随机共振处理结果相比,本文所提方法在检测低浓度NH3信号时,输出信号频谱在输入信号频率处的频谱峰值更大,更突出,也即共振现象更明显,尤其对于3×10-9、6×10-9这些极低浓度的气体,共振现象更突出,可以更容易将微弱的低浓度气体信号检测出来,并且有利于提高系统检测的效率。

图9 遗传算法随机共振系统输出信号频谱图

NH3浓度和对应的SNRmax值之间的关系如表1和图10所示。

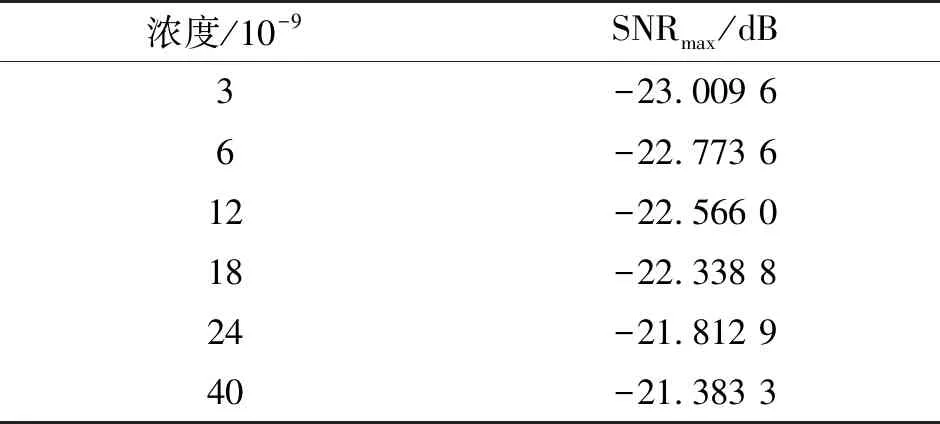
表1 氨气浓度与SNRmax值

图10 氨气浓度与SNRmax值的关系图

从表1和图10可以看出,随着NH3浓度的增大,其对应的SNRmax值也随着增大,根据表1中的数据,可以拟合得到气体浓度和系统输出信号的SNRmax值之间的关系,如图10所示,其回归方程为:

y=0.044 46x-23.08

(7)

式中x是气体检测浓度(单位:×10-9),y是相应的SNRmax值(单位:dB),此方程的R-square和RMSE分别是0.970 1和0.118 4。该方程表明气体浓度和系统输出信号的SNRmax值之间存在近似的线性关系,可以通过随机共振的SNRmax值估计气体浓度。

2.3 验证分析

图11 x1和x2浓度NH3的输入输出信号频谱图

为了验证上述遗传算法随机共振方法检测低浓度气体的可行性,本文对两种未知浓度的NH3(x1和x2浓度)电阻信号进行处理。实验结果如图11所示。从图11中可以看出,两种浓度的NH3电阻信号经共振处理后,在输入信号频率fc=0.1 Hz处的频谱值均显著增大,并且非常突出,出现了明显的随机共振现象。

由实验可得到,两种未知浓度的NH3信号对应的SNRmax值分别是-22.676 0 dB和-21.802 7 dB,根据式(7),分别计算得到气体估测浓度约为9.1×10-9和28.7×10-9,而采用气敏传感器测量的实际浓度分别是8×10-9和30×10-9。实验还进一步检测了其他未知浓度NH3的浓度,并对估测结果进行了误差分析[18],如表2所示。可知,本文所提方法的估测结果与气敏传感器测量的实际气体浓度误差在 1×10-9左右。验证实验结果表明,本文所提方法在低浓度气体的浓度检测中具有一定的可行性和有效性,气体浓度检测的误差在1×10-9左右。

表2 气体浓度误差分析

3 结论

本文结合最优化理论和随机共振,提出一种自适应随机共振系统,以系统输出信噪比为适应度函数,通过遗传算法自适应并行优化参数a、b、D来获得最优共振系统,为工程应用上高效选取随机共振系统的多个参数,以达到最佳共振状态提供了一个很好的方法,并将其成功应用到了低浓度气体检测中。实验结果表明,所提方法可以有效实现低浓度气体的检测,并且发现气体浓度和SNR的最大值之间存在近似线性关系,为估测气体浓度提供了一种可行的解决方案。