金属腐蚀区域图像增强算法研究

雷芳，熊建斌，张磊，郭斯羽

（1. 广东石油化工学院 计算机与电子信息学院，广东 茂名 525000; 2. 广东技术师范学院 自动化学院，广东 广州 510665; 3. 湖南大学 电气与信息工程学院，湖南 长沙 410082）

金属材料受到环境因素的影响其腐蚀表面呈现形貌纹理、灰度、颜色等不同特征。通过对这些特征的分析可识别材料腐蚀的程度和腐蚀的类型[1-2]。在腐蚀无损检测的远程视觉检测(remote vision inspection，RVI)检测中，主要是使用视觉设备来获取腐蚀信息。对于金属外部腐蚀，可以采用摄像机或CCD相机获取腐蚀图像，设备内部腐蚀图像的获取主要有管窥镜、自动爬行器等设备。通常为了提高腐蚀原图像质量，可以从内部和外部两方面来进行实施[3]：1)对图像采集的外部环境进行改善；2)对采集的原图像质量进行有效增强。而众所周知，在对金属设备的腐蚀自动视觉检测中，其外部环境往往比较难以控制，比如，距离、角度、光源等影响腐蚀图像质量的因素都会受到所处环境的限制。所以，通常为了后续腐蚀形貌的检测与识别工作，对采集的腐蚀原图像进行有目的性的增强就显得意义十分重大[4-6]。

当前，图像增强算法主要有直接针对像素灰度处理的增强算法[7-8]、基于色感一致性模型的单尺度Retinex及多尺度Retinex(MSR)增强算法[9-11]、同态滤波增强算法[12-13]、基于暗通道先验理论的去雾增强算法[14-15]等。在上述图像增强算法中，对像素值的直接处理可改善图像亮度动态范围但易丢失细节信息或色彩失真；Retinex增强和同态滤波增强都进行了对数变换，前者是通过估计照度分量得到物体的反射分量，在图像亮度保持和细节这两方面的处理效果都比较好，但容易造成偏色等色彩失真现象[16]，后者是利用同态滤波函数压缩低频分量与增强高频分量来改善光照不均的影响；而去雾增强算法是将每个颜色通道中接近零的灰度值描述为暗通道并将其近似为图像中雾的浓度，通过去雾实现增强，但该算法对不满足暗通道原理的图像增强效果并不理想[17]。在有关Retinex和基于暗通道原理的去雾彩色图像增强算法中，王建新等[15]在HSI模型中建立了去雾模型，秦绪佳等[16]在HSV模型中建立Retinex增强模型，这两种模型都需要根据亮度分量的调整进而调整单一饱和度或同时调整色度与饱和度分量，这使得色彩保真度在颜色恢复过程中将受到对应分量调整的影响。小波变换具有时频与多尺度特性，针对不同分辨率下的小波系数进行非线性增强可以实现图像的增强[18]。文献[19]中，孙慧贤等提出了基于小波变换和同态滤波的内窥图像增强算法，该算法是在传统同态滤波中用小波变换替代傅里叶变换，然后对不同分辨率下的小波系数进行非线性增强，该算法的不足是在图像经过了对数运算后再对不同尺度下小波系数的非线性调整，因此重构图像易出现“伪像”的问题。

针对现有算法存在的问题，本文受到自适应细节增强[19]算法的启发，结合同态滤波具有全局性质的特点但同时存在局部对比度增强效果不理想的问题，提出一种HSI模型下的多尺度细节自适应增强与同态滤波的金属腐蚀区域图像增强算法。本文算法具体如下：首先将腐蚀图像从RGB颜色空间转换至HSI颜色空间，提取亮度分量；利用小波变换的多尺度特点对腐蚀细节进行局部对比度增强然后将细节增强后的图像作分块同态滤波；最后，将新的亮度分量与原饱和度和色度分量一起转换为RGB图像，得到增强后的腐蚀图像。实验结果表明，本文算法在不改变H分量和S分量的基础上，能很好地增强腐蚀缺陷细节并且腐蚀色彩特征保持良好，增强后的图像有利于进一步的金属材料腐蚀损伤分析。

1 本文方法

腐蚀图像的增强问题主要是腐蚀暗细节的加强以及光照不均影响的消除。在保留腐蚀产物颜色特征的同时，能将腐蚀斑或腐蚀坑等腐蚀细节很好的显现出来。

本文方法整体流程如图1所示：选取HSI模型提取金属腐蚀图像的亮度分量，然后再对细节进行多尺度增强后采用分块同态滤波的方式改善图像的亮度。在整体处理中避免改变H分量和S分量，只在I分量上做增强处理，因此不会改变原图像中的彩色种类，使最后图像在色彩上和原始图像保持一致。

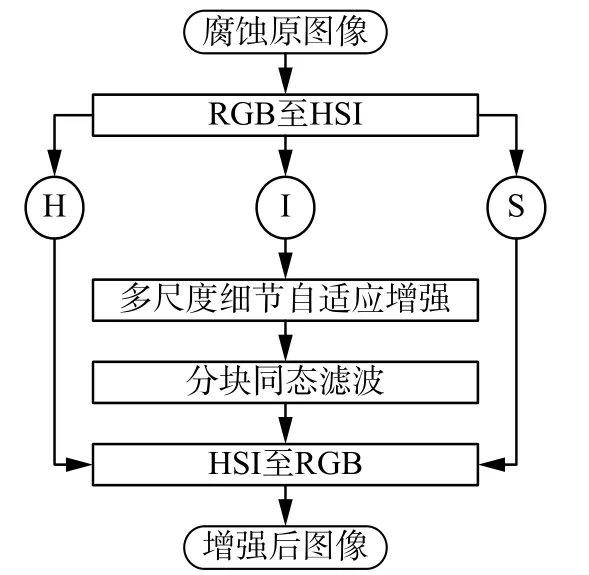
图1 提出方法流程图Fig.1 Flow chart of proposed algorithm

1.1 腐蚀处理中的HSI模型应用

原始获取的图像是RGB颜色空间，图像中像素的颜色采用红(R)、绿(G)、蓝(B)三原色的不同比例来描述，该模型适合于人眼对上述3种颜色的敏感性，但不适合解释颜色。HSI(色调、饱和度、亮度)模型更加符合人眼视觉系统描述和颜色的解释[20]，该模型能将颜色与亮度分开，更适合腐蚀图像中的暗细节表示。

RGB模型转换为HSI模型的公式如式(1)：

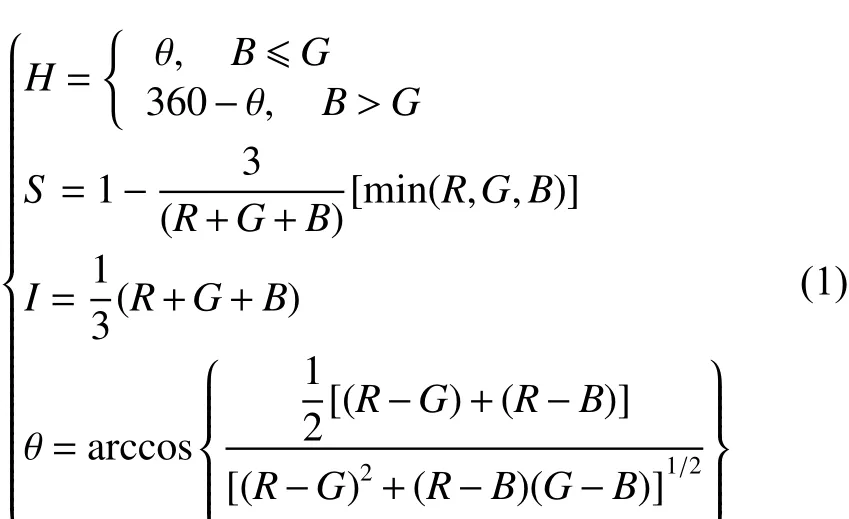
由式(1)可以看出，H分量表示整体色调值，其在0～2π之间变化。当像素只有R分量时，H值为0度；只有G分量时，H值对应120°；只存在B分量时，其在240°。而S分量在0～1之间，如果当前像素缺少RGB中某一个分量，S值为1，即S值越接近于1，表示颜色越纯。而在RGB成分相同时，即为灰色时，S值为0。对于I值，它是原始图像RGB 3个通道的平均，因此整体反映图像亮度的信息。

针对腐蚀图像颜色特点，由文献[5]可知，对于金属腐蚀表面来说，其色调分量的值通常在黄色和红色波长之间；由于金属表面通常以浅灰色和白色涂覆，所以被腐蚀的金属表面的饱和度分量的值通常更大，即颜色较深；而未腐蚀的表面的颜色则倾向于高亮度的白色波长。本文选取HSI模型对腐蚀颜色进行描述，保留腐蚀色彩的色度分量和饱和度分量，只对亮度分量进行图像增强处理。在最后将其还原回RGB空间表示，这时由HSI模型转换为RGB模型的公式如式(2)所示：

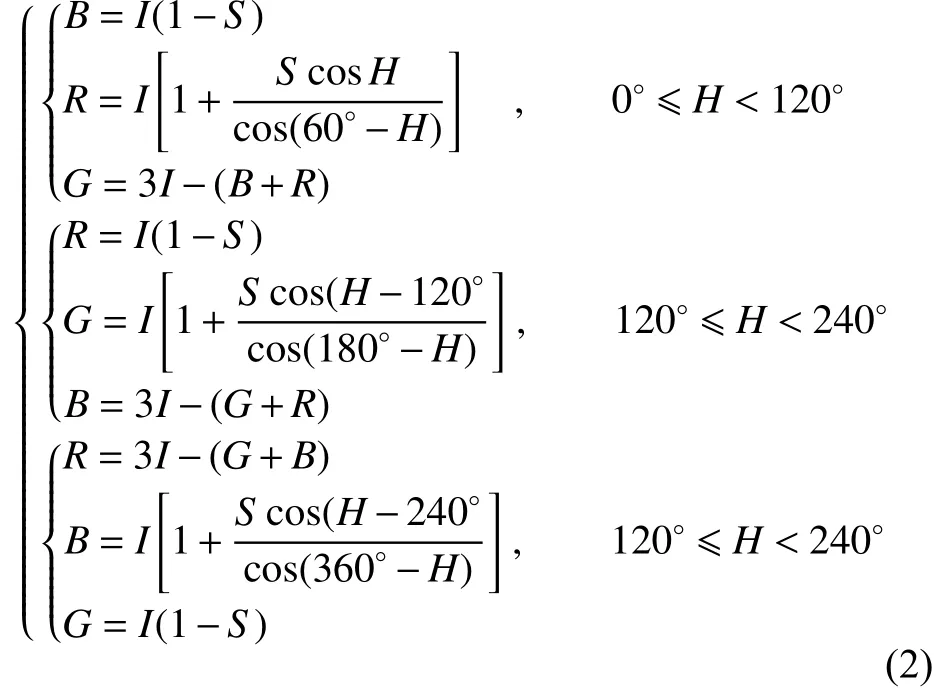
1.2 多尺度细节自适应增强

由于腐蚀细节的尺寸大小不一，与背景的对比度也有强有弱，因此在不同分辨率下对腐蚀细节进行对比度分析比单一分辨率下分析更具优越性。小波分析具有很好的多尺度特性，选取合适的小波基函数可以将图像分解为不同尺度的近似图像和细节图像，在变换的每一层中图像都被分解为4个四分之一大小的图像[21]。在小波逐级分解过程中，需选择合适的分解层数，如果分解级数太少则近似图像中将包含过多细节分量使得细节增强不够，而分解级数过多会使得计算量增大。本文对小波进行3级分解，可满足腐蚀细节增强要求。

为了对腐蚀图像的细节进行多尺度增强，需要调整不同尺度下细节分量的系数。关于各细节分量系数的调整，若直接设置具体的数值，将会使得算法受限不具备自适应性。根据文献[18]，小波分解的细节图像的系数自适应调整，是通过计算其相同尺度的近似图像的全局对比度得到。

如图2所示，为图像进行3级小波变换后近似分量中像素点P的3×3邻域。算法思路为：先计算近似分量中每个像素点邻域内的对比度(最大值与最小值之差)并归一化，再求所有像素点的对比度之后，得到近似分量的全局对比度Cglobal，最后由全局对比度计算出各细节分量的权重调整因子 K，并对细节增强图像进行重构。相关公式及具体过程如下：

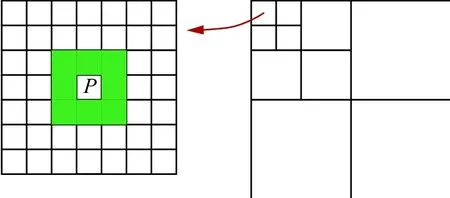
图2 近似分量中像素点P的3×3邻域Fig.2 3×3 neighbor of pixel P in similar component

1) 计算图像 f (x,y)的 最大值 fmax和最小值 fmin。

2) 对每级分解图像近似分量进行非线性滤波 ， f(xi,yi)=(max(xi)-min(xi))/(fmax-fmin)。 其 中max(xi) 和 m in(xi) 为滤波过程中心像素邻域内的最大值和最小值。

3) 计算第 i 级图像近似分量的全局对比度，其值为 Cglobali=c0·Lsumi/num(fi) 。 其中， Lsumi为非线性滤波输出图像的像素值之和， n um(fi) 为图像的像素点个数， c0为对比度调节因子，一般取值范围为 1.0～1.1。

4) 引入第 i 级全局对比度权重因子 Ki，其中，。将其与细节分量的系数相乘，调整细节图像。

5) 在调节细节分量的同时，也可根据实际需要将近似分量乘以亮度因子 L0，其一般取值范围为 1.0～1.2。

在步骤6)图像重构过程中，首先是对第3级小波分解的细节分量和近似分量进行系数调整和图像重构，然后依次调整第2级和第1级各分量并重构，最后获得细节增强的亮度图像。

1.3 分块同态滤波

对于金属腐蚀图像而言，由于大部分自然环境中采集的腐蚀图像受到光照不均匀影响，使得一些图像整体亮度不够，易导致经多尺度自适应增强后的细节淹没在暗的背景中。腐蚀细节不能正常识别，将不利于对金属腐蚀状态进行诊断，分块同态滤波可以减少图像亮度的动态范围以及增强对比度从而使背景处的暗细节显示出来。

同态滤波的原理是将图像看作光源的入射光分量和物体的反射分量的乘积，可用g(x,y)=i(x,y)·r(x,y)描 述。其中， i (x,y) 被视为图像的入射光分量，它通常变化缓慢因此主要集中在低频带，r(x,y)被视为反射分量，反射光通常变化快，主要反映在高频带。对图像进行同态滤波的优点主要体现在它能压缩图像的低频成分并增加其高频成分，从而减少光照变化，有效弥补光照不均对物体的影响，同时还能锐化图像的边缘或细节[22]。

同态滤波算法的实现原理如图3所示，先对多尺度细节自适应增强图像取对数运算实现将其入射光分量和反射分量分开的目的；应用快速傅里叶(DFT)算法，将其从空域变换至频域，接下来选择合适的同态滤波函数 H (u,v) 对图像进行滤波，然后对滤波后的图像进行傅里叶逆变换(IDFT)，将图像从频域转换为空域，最后再取指数得到增强后的亮度分量图像。

图3 同态滤波流程图Fig.3 Flow chart of homomorphic

在图像同态滤波过程中，对于能否达到理想的滤波效果，滤波函数的选取至关重要。一般同态滤波函数均选择能减少低频分量和增加高频分量的滤波器，其中最常用的滤波器有高斯型同态滤波器和巴特沃斯型同态滤波器。本文同态滤波传递函数选用高斯型同态滤波器，如式(3)所示：

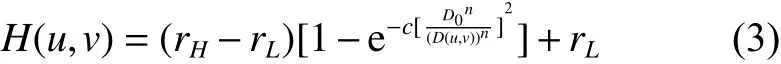
式中： rH、 rL为亮度调节因子， rH增强高频分量，其值越大图像越亮，而 rL抑制低频分量，其值在不超过 rH时，对增强效果影响不大。一般 rL＜1，rH＞1 ， c 为常数，在上述两个因子之间取值，通常取1.0。 n 为滤波器的阶数， D0为截止频率，它的值与入射分量和反射分量有关，其值越小则意味着滤波后留下的低频分量越多，图像越暗，相反则图像越亮，其值的快速计算方法可通过对D(u,v)进行中值运算实现。 D (u,v) 为 点 ( u ,v) 到傅里叶变换中心的距离。根据图像大小为 M ×N 的傅里叶变换中心位置为 M/2、 N /2 ， 可得 D (u,v) 计算公式：

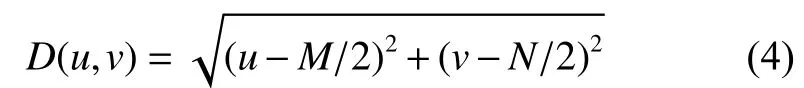
图像的同态滤波可按整体的方式进行也可局部或分块进行。由文献[13]的对比实验可知，对图像进行同态滤波时，从整体的方式出发会导致增强后的图像某些部分过亮，造成一些细节损失，而采用分块的方式则增强后的图像明暗适中，细节清晰。

根据上述分析，本文采用分块的方式进行同态滤波，如图4所示。考虑到滤波过程是在图像子块中进行，增强后的整体图像在子图像块之间的边界处不可避免地会产生块效应。图4中，粗线条表示产生块效应的子图像边界，灰颜色方格则表示需要修改像素值的像素位置。为此，在图像按块方式同态滤波后还要从水平和垂直两个方向对图像进行块效应消除。为降低计算复杂度，本文采用邻域均值法去除块效应，即将块与块图像边界处的像素值取以边界像素为中心的3×3邻域内的均值作为该位置的像素值，具体见式(5)～(8)。

图4 同态滤波及其块效应Fig.4 Homomorphic and block effect

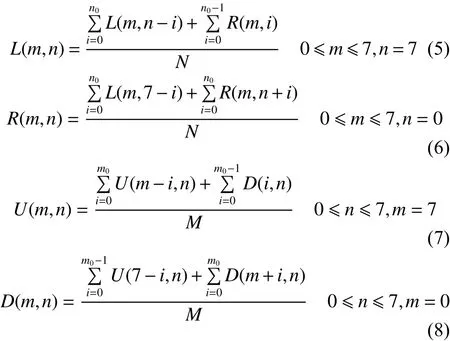
式中：L 和 R 为水平方向上的子图像，U 和 D 为垂直方向上的子图像，M 和 N 为邻域模板的大小，n0= fl oor(N/2)，m0= fl oor(M/2)。

2 实验结果与分析

本文对金属腐蚀区域图像的增强算法进行了研究，提出了HSI模型下多尺度细节自适应增强与同态滤波的腐蚀图像增强算法，并将算法应用于金属管道腐蚀图像的增强。为了研究金属管道材料在特定环境下自然腐蚀的情况，实验中使用的腐蚀图像均采集于某输油站场内暴露于自然环境下已经被腐蚀的金属管道材料，图5为现场实物图，从图中可以看出金属管道的许多区域已经受到了自然环境的腐蚀。

图5 自然环境下受到腐蚀的金属管道Fig.5 Corrosion metal pipeline in natural environment

为了验证提出算法的增强效果，本文选取3幅腐蚀形态相异，亮度不均匀、腐蚀细节对比度低的腐蚀原图像作为实验图像，腐蚀原图及其亮度分量如图6所示。

图6 腐蚀原图像及I分量Fig.6 Corrosion image and I component

在对管道腐蚀图像增强算法的对比实验上，采用小波自适应增强算法、同态滤波算法、MSR增强算法、暗通道去雾增强算法以及本文算法作比较。上述所有算法在实验中都只针对金属腐蚀图像的I分量进行增强，再将增强后的I分量图像与原图像的H分量、S分量进行色彩空间变换转换为RGB图像，最后得到增强的金属腐蚀图像。具体实验结果见图7～9。

图7 腐蚀图像1增强效果比较Fig.7 Enhancement results comparison in corrosion image 1

图8 腐蚀图像2增强效果比较Fig.8 Enhancement results comparison in corrosion image 2

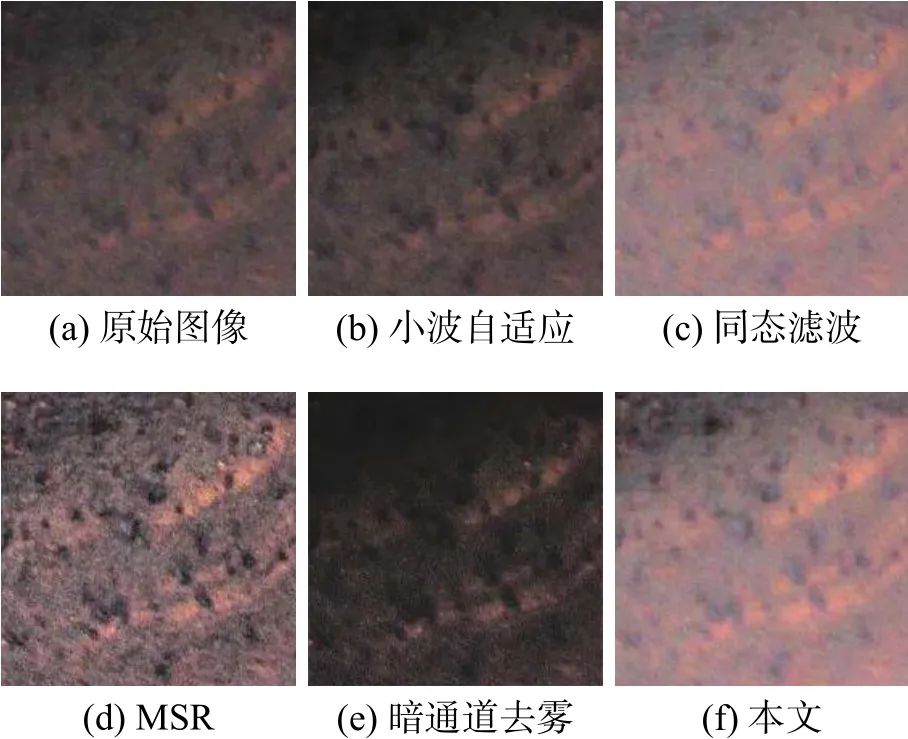
图9 腐蚀图像3增强效果比较Fig.9 Enhancement results comparison in corrosion image 3

实验中，小波变换的基函数名称为db1，参数c0取 1.0，L0取 1.2；其中，c0作为图像的对比度调节因子，用来调节图像的细节分量；而L0为图像的亮度因子，调节图像的亮度分量。在分块同态滤波中，其中的参数rH取1.2，rL取0.5；它们分别用来调节图像的低频部分和高频部分；同态滤波器的阶数n=1，其中心截止频率D0=median(median(D))。

关于不同图像增强算法效果的评价，本文采用人眼观察的主观评价和图像信息熵的客观评价两种方式进行评价。主要包含两部分：1)根据人眼视觉主观感受去比较增强图像与原图像之间的区别；2)用度量图像信息量大小、图像细节丰富程度的指标熵对图像增强效果进行客观评价。

首先，从图7～9中的(a)图发现，金属腐蚀区域图像均出现原图整体亮度偏暗的问题，造成图像中某些部分的腐蚀暗细节根本无法从背景中被识别出来，从而直接影响被检区域的腐蚀程度检测；图中的(b)为小波自适应增强算法后的结果图，可以看出小波增强结果图相较于原图虽然对腐蚀细节分量有很强的增强效果，但由于无法提高腐蚀图像整体亮度，从而使得腐蚀斑点或腐蚀坑区域更加不易从背景暗区域中被识别出；图中的(c)为同态滤波后的增强图，从对比实验中发现对腐蚀原图像同态滤波后能很好的提升图像的整体亮度，弥补了光照分布不均的缺陷，使得人眼能够很容易从图像中看出腐蚀斑点或腐蚀坑位置，但不足之处是某些位置的暗细节被弱化了，从而导致腐蚀坑等区域不被发现；图中的(d)为MSR算法增强后图像，从图中可以看出增强后图像可以很好的将腐蚀缺陷细节显现出来，但是在亮度改善上效果并不明显，而且在一些区域上出现了色彩的失真；图中的(e)为暗通道去雾增强算法，去雾后的图像比较清晰，但很多腐蚀细节不能从背景中识别；图中的(f)即本文算法，从实验结果图发现本文算法在腐蚀细节显现、亮度改善及色彩保真上均优于上述几种算法。

表1为对图6所示的原图像亮度分量信息熵与采用不同增强算法后亮度分量的信息熵。表2是在一个包含20幅腐蚀图像的数据集中计算图像信息熵的均值与方差。熵是衡量图像信息丰富程度的一个重要指标，熵越大表示图像包含的信息量越多，信息越丰富则图像质量也越好[23-24]。因此，本文通过计算增强后亮度图像的信息熵来对增强图像进行客观评价。

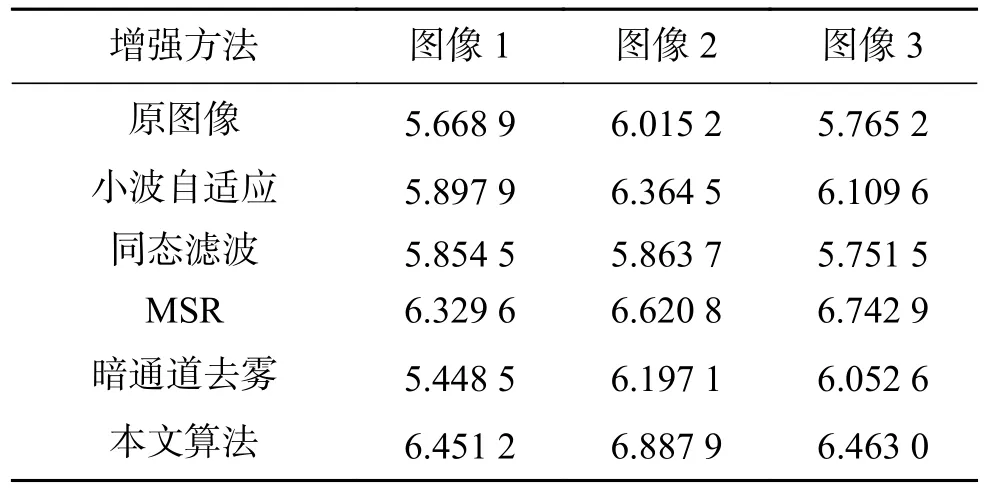
表1 各图像亮度分量的信息熵Table1 Entropy of intensity component in each image

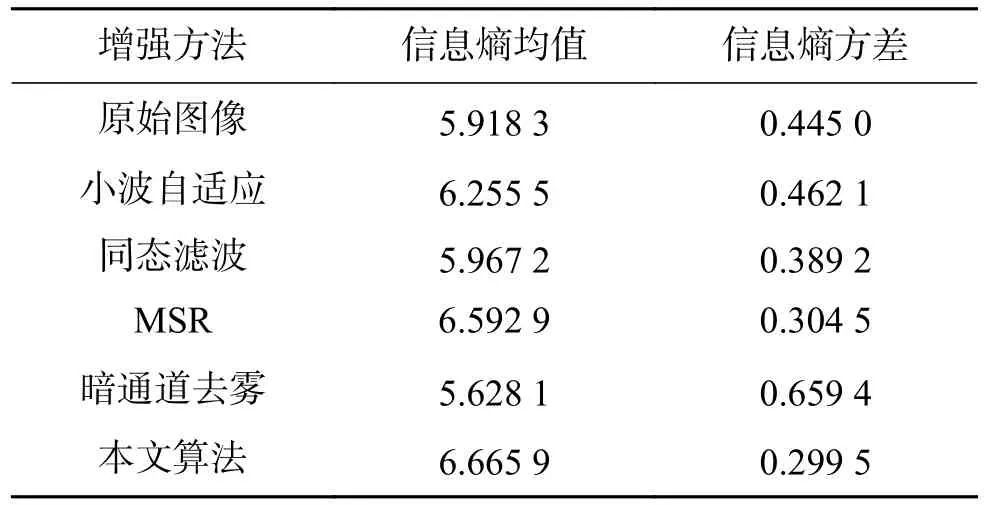
表2 图像集的信息熵指标对比Table2 Entropy index comparison in image set

从表1中数据发现，不同增强算法对腐蚀原图像亮度分量信息熵的影响不一样。对表1的每一列进行比较，发现小波自适应、MSR与本文算法均增加了原图像亮度分量的信息熵；同态滤波和暗通道去雾算法并没有增加每幅图像的信息熵，甚至还出现了显著下降；在对图像信息熵有明显增加的3类算法中，MSR算法和本文算法的增加效果最为明显，其中，除了图3的熵值本文算法低于MSR算法，图像1和图像2的熵值本文算法均高于MSR算法。从图9中可以看到图3的各算法效果增强图，MSR增强图虽然在细节凸显上高于本文算法，但色彩及纹理有失真，而本文算法既能凸显腐蚀细节又保证了腐蚀颜色特征的不失真。

从表2中数据发现，在对腐蚀图像集应用本文算法后得到的平均信息熵高于其它几种算法，且本文算法的信息熵方差最小。因此，相较于其它增强算法，本文算法增强效果的整体性与一致性更好。

根据腐蚀图像增强的实际应用要求，综合上述主客观分析可知，应用本文算法对金属腐蚀区域图像进行增强可以得到较好的主观视觉效果，同时还可以提高原图像的信息熵。

3 结束语

本文通过HSI模型提取金属腐蚀图像的亮度分量，并对亮度分量中的腐蚀细节进行多尺度增强，以及同态滤波来改善图像光照不均的影响，从而实现对金属腐蚀区域图像的增强。本文算法虽应用了小波多尺度变换与同态滤波的理论，但不是同已有文献一样将小波变换替代同态滤波里的傅里叶变换，而是先对图像进行多尺度细节增强重构然后再应用分块同态滤波。在不改变图像色度和饱和度分量的基础上，本文算法相比其它算法具有更好的色彩保真度和细节对比度，能有效的用于金属腐蚀区域图像的增强，对金属腐蚀产物的进一步研究分析具有重要的意义。

由于本文算法需要进行多尺度细节增强与分块同态滤波两步处理，使得算法的时间开销比较大，因此本文下一步的工作主要为提高算法的实时性。