28÷12=280÷120吗*
——有余数除法中的余数到底是什么
2019-04-10章勤琼
□ 章勤琼
在某地区小学数学四年级上册的期末考试中,出了这样一道题:“在○里填上‘<’‘>’或‘=’,28÷12○280÷120。”
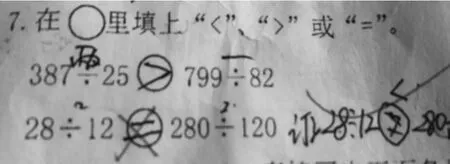
图1
如图1所示,学生写了“=”,却被判了错误,并在后面订正为“28÷12<280÷120”。此题引起了很大的争议,有人认为此题应该是相等的,因为“被除数和除数同时乘或者除以一个数,商是不变的”。但也有人提出了不同的看法,认为“虽然商不变,但是余数会变化。这道题应该是小于,原因是如果把两边的式子计算出来,商相同,但余数并不相等。因为28÷12=2……4,而280÷120=2……40,商2和2是一样的,而余数40比4要大,所以280÷120更大一些”。理由是“商相同时应该比余数”。也有人对这个题目本身提出了疑问,“这道题目是要比较余数的大小还是比较结果的大小?如果是比较余数的大小,应该是小于,如果题目是比较结果的大小还是应该等于”。
那么,这道题目的答案到底应该是等于还是小于呢?我们应该对与此相关的数学概念进行一些梳理,进而对教学进行进一步的思考。
一、“除法”与“有余数除法①“有余数除法”也叫“带余除法”,两者同。”
要讨论28÷12和280÷120是否相等,需要先弄清楚什么是除法。在现代数学中,一般是这样定义的:“除法是数学中的基本运算之一,已知两个数a,b(b≠0),要求一个数q,使q与b的积等于a,记为a÷b=q。……a称为被除数,b称为除数,q称为它们的商。”[1]而在我国的小学数学教材中,学生一般在二年级开始学习除法,教材中并没有给出除法的定义,都是结合生活实例,让学生在分一分的活动中,在积累大量平均分经验基础上引出除法,而这些分一分的活动,既有按份数平均分(等分除),又有按每份数平均分(包含除)。
从定义中可以看出,在一个除法算式中,有3个数,分别是被除数、除数和商。事实上,所有的运算都应该是一种对应。而“对于自然数来说,我们可以认为算术运算是为一对自然数m和n指定一个自然数,其中m和n的顺序不可改变。在自然数的前提下,算术运算的结果是一个单独的(自然)数”。[2]清楚这一点,对于我们理解运算是有帮助的。在加减乘除四则运算中,自然数对于加法和乘法运算是封闭的,即任意两个自然数经过加和乘之后仍然是自然数。但自然数对于减法和除法运算却不封闭,两个自然数相减,有可能出现负整数,如要对减法封闭,就要将数系扩充到整数;而两个自然数相除,则可能出现分数(或小数),如要对除法封闭,就要将数系扩充到有理数。
而有余数的除法,是指“一个整数除以另一个不为零的整数,得到整数商后还有余数,这样的除法叫作有余数的除法。有余数除法的意义也可以这样表述:已知两个整数a,b(a≠0),要求这样的两个整数q,r,使得q,r满足:b=aq+r,r<a,这样的运算叫作有余数除法。求得的整数q叫作不完全商,r叫作余数。b、a仍然分别叫作被除数和除数,这四个数的关系记作b÷a=q……r,(r<a)”。[3]
由于都叫除法,人们容易把“有余数除法”看成是“除法运算”的一种特殊形式,但如果用对应的方式来看,这两者存在着本质的区别。有余数的除法为两个有序的自然数m和n(n≠0)规定了一对自然数与之对应,这对自然数就是m与n做有余数除法所得的商和余数。“有余数的除法为任意一对自然数m和n(n≠0)规定了两个而不是一个自然数与之对应,这一事实使得它不够资格成为算术运算。”[4]我们可以对有余数除法与除法进行如下这样的比较[5]:
(1)“有余数除法”是定义在整数集上的一种运算;而“除法”可以在任何一种数集上定义。
(2)两种除法的定义虽然都与乘法有关(所以它们都被称之为“除法”),都要求除数不等于0,但具体条件不同:
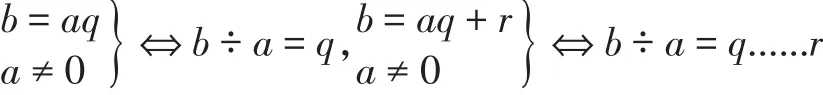
(3)不能说“有余数的除法是除法的特例”,也不能说“除法是有余数除法当r=0时的特例”。它们的关系并不是属种关系。
因而,在等式“28÷12=2……4”中,符号“2……4”并不是28与12两数相除的商。而是因为自然数对除法运算不封闭,无法找到一个自然数对应表示商所采取的一种特殊的表示方式,其表示的结果不代表任何确定的数。实质上它只给出了商的整数部分与分数部分的分子,分数部分的分母则是等号另一边的除数。即28÷12=2……4的意思为28÷。因此,当“2……4”即“2”单独出现时,由于分数部分的分母不确定,所以它不能表示确定的数。同样道理,在280÷120=2……40中,“2……40”所表示的如果单独出现,由于分数部分的分母不确定,也不能表示确定的数。那么,单独比较“2……4”与“2……40”的大小当然就毫无意义。由此,我们可以知道,前面有人提到的“商相等,比较余数大小”在数学上行不通,是一种错误的方法。
不妨来看另一个例子,25÷6=4……1与21÷5=4……1。因为这里的“4……1”不代表任何确定的数,我们同样不能因为计算的结果都用“4……1”来表示,从而判定25÷6与21÷5相等。更进一步地讲,虽然都是“4……1”,但两个式子中余下来的“1”的意义是不一样的,前式的除数是6,因此“1”是“6”当中的“1”,而后式的除数是5,因此“1”是“5”当中的“1”。也许有人会说,如果把25÷6看成a,把21÷5看成b,把4……1看成c。就有a=c,b=c,根据等式的传递性,应该有a=b。为什么在这里,等式的传递性不成立?需要再次强调,在这里“4……1”并不是两数相除的商,不是一个确定的数,自然不能看成是“c”,那么,就不能为a与b的相等起到传递作用。所以,并非是等式的传递性不成立。
有余数除法的结果用“商……余数”表示,的确容易引起一些混乱。有学者甚至指出,“应当把25÷6=4……1这种记法清除出所有的教科书,因为它(在数学上)没有任何意义。……正确的表示有余数除法的方式是‘25=(4×6)+1’”。[6]在小学阶段,恐怕无法完全避免“4……1”这样的表示形式,但需要明确这种形式并不能作为两数相除的结果。而在有余数除法中,无视除数直接采用“商相等比余数”的方法更是完全错误的。同时,也的确需要更加注重“被除数=商×除数+余数”这样的表达方式。
二、商的变化规律
既然在比较28÷12和280÷120的大小关系的时候,不能用“商相等比较余数”的方法去比较得到280÷120>28÷12,那么,该如何比较28÷12与280÷120的大小呢?
第一种方法当然是真正算出这两个除法算式的商,所谓真正算出,是指找到一个确定的数来对应28÷12和280÷120的运算结果。很显然,在自然数范围内找不到这个数,那么需要扩充到有理数范围,即用分数或小数来表示商。这两个商都是带分数,整数部分都是2,根据分数的基本性质,分数部分。因此,它们的商相等,根据等式的传递性,有28÷12=280÷120。也可以用小数来表示商,28÷。同样可以利用等式的传递性,得到28÷12=280÷120。
但是,这道题是四年级上册的期末考试题,商是小数或分数的除法还没有学过。那么,学生是否还有其他方法解决这道题目呢?
在四年级上册,学生已经学习了商的变化规律(人教版)。教材中明确指出:“被除数和除数都乘一个相同的数,商不变。”“被除数和除数都除以一个相同的数,商不变。”而在后面又特别强调了“应用商的变化规律不仅可以使口算简便,还可以使笔算简便”。[7]如果运用商的变化规律,将28÷12中的被除数和除数同时扩大10倍,变成280÷120,商不变,因此,28÷12与280÷120相等。
不需要算出结果,直接运用商的变化规律来判断,这应当也是出题者的初衷。这样来看,这道题判断起来似乎并不困难,更不应该出现这么大的争议。究其原因,大概是因为四年级上册在学习商的变化规律时,所有的算式都是可以整除的,并没有出现有余数的情况。而在教学商的变化规律的时候,通常会让学生将商计算出来再进行判断。而在本题中,计算结果的时候出现了余数,“结果”并不完全一致,所以造成了困惑。但如果明确一个事情,商的变化规律不仅适用于能整除的除法算式,还适用于不能整除的算式,这个问题就迎刃而解了。
三、两点教学建议
第一,在学生初次接触余数时,注意强调余数与除数的相互关系。之所以出现文章开头的这个问题,其根本在于没有很好地理解余数的意义。有研究者就曾指出“学生对余数的掌握只停留在技能的操作层面上,并没有更深层次地把握余数的意义。导致产生这一问题的重要原因是,教师在课堂教学中过分注重基础知识和基本技能的培养。这样,尽管学生掌握了不少有关余数的知识,但教学中的‘强化训练’忽略了对余数实质的理解,学生体会不到涉及其本质的关键性问题”。[8]
学生在二年级下册开始学习除法以及有余数的除法(人教版),在有余数的除法的教学中,主要有以下三个方面的内容:一是用生活情境引出余数;二是余数要比除数小;三是有余数除法的竖式计算。虽然教学中有强调余数比除数小这样的关系,但对于余数与除数之间这种千丝万缕的关系,如“余数是相对于除数而言的”“不能脱离除数谈余数”等的关注不够。因此,在学生初次接触余数时,可以设置巧妙的教学活动,除了使学生认识到“余数比除数小”以外,还可以使他们认识到这样一个问题:余数并不是单独存在的,余数与相应的除数有关,余数随着除数的变化而变化。[9]这对于学生后续相关内容的学习是有帮助的。
第二,在运算教学中,重视对等式性质与运算法则的理解。如在学习商的变化规律时,应该淡化通过计算出商来判断除法算式的相等关系。商的变化规律的得出需要借助观察商的大小,但是在理解变化规律之后进行运用的时候,可以不再把商算出来。因此,一方面,在判断像28÷12和280÷120这样的式子的大小关系的时候,应该注意直接运用商的变化规律来进行判断,而不应该过分强调要分别计算出结果来进行判断;另一方面,在教学商的变化规律时,除了整除的式子以外,可以有意识地增加一些不能整除的式子,在一定程度上引起学生的认知冲突,从而帮助他们更好地理解规律,而不是一味地先计算出商再来对结果进行比较。
更进一步地进行分析,如图1中的第一道题,387÷25○799÷82,根据学生的答题记录,我们可以看出,学生先判断左边式子的商是两位数,右边式子的商是一位数,因此左边大于右边。这当然是很好的方法,但还是先算出商再进行比较,只是这里用的是估算。其实还能引导学生运用另外一种思路进行判断,如果比较左右两个式子,被除数799小于387的3倍,而除数82大于25的3倍。根据商的变化规律,被除数扩大的倍数小于除数扩大的倍数,商会变小,因此,387÷25>799÷82。这样的思考方式,更多关注式子的变化和关系,学生对于等式以及运算性质的理解更加深刻,对于今后的代数思维的发展有更大的帮助。
运算能力是义务教育数学课程标准中明确提出的十大核心概念之一,“运算能力是指能够根据法则和运算律正确地进行运算的能力”。[10]“正确地进行运算的能力”显然不是仅指快速准确地得到计算结果,运算能力的内涵也要丰富得多,比如有研究者就指出运算能力应包含四个方面的内容,分别是基本口算、理解算理、掌握算法以及运算策略。[11]而“根据法则”中的法则即运算法则,包含了加减乘除等运算的各种性质。商的变化规律的理解与掌握是运算法则的一部分,对于学生运算能力的发展至关重要。
